CBSE Important Questions for Class 6 Maths The Other Side of Zero - 2025-26
FAQs on CBSE Important Questions for Class 6 Maths The Other Side of Zero - 2025-26
1. What types of questions are typically asked from CBSE Class 6 Maths Chapter 10, The Other Side of Zero, in exams?
For the 2025-26 session, important questions from this chapter primarily focus on representing integers on a number line, comparing positive and negative integers, and performing basic addition and subtraction of integers. Expect a mix of multiple-choice questions (MCQs), fill-in-the-blanks, and short-answer problems that test these core skills.
2. How can practising important questions from Vedantu for Chapter 10 help in the final exams?
Practising these curated important questions helps you identify recurring patterns and high-priority topics for the exam. It strengthens your application of key concepts like the number line and integer operations, which are crucial for scoring well. This targeted practice builds confidence and improves both speed and accuracy for the final assessment.
3. What are some examples of 1-mark or 2-mark questions that can be expected from this chapter for the 2025-26 exams?
For the 2025-26 exams, short and objective questions are very common from this chapter. You can expect problems such as:
- Writing the opposite of a given integer (e.g., the opposite of -23).
- Representing an integer like -6 on a number line.
- Comparing two negative integers (e.g., which is greater: -9 or -3?).
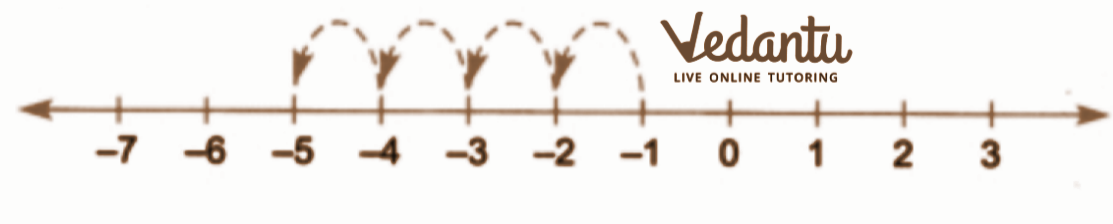
- Solving simple additions or subtractions like (-8) + 5 or 4 - (-2).
4. Why is a strong understanding of the number line so critical for solving important questions on integers?
The number line is more than just a diagram; it is a fundamental conceptual tool. It is critical because it helps you visualise the magnitude and position of numbers. For exams, a solid grasp of the number line is essential for correctly solving problems involving integer comparison (understanding why -2 is greater than -10), addition, and subtraction, thereby preventing common sign-related errors.
5. How are real-life scenarios like temperature and altitude used to frame Higher Order Thinking Skills (HOTS) questions in this chapter?
HOTS questions test your ability to apply mathematical concepts. Instead of a direct calculation, an exam question might be framed as: "A submarine is at a depth of 50 metres below sea level and ascends 20 metres. What is its new position?" These application-based questions require you to first translate the real-world problem into a mathematical expression (-50 + 20) and then solve it, testing a deeper understanding beyond rote memorisation.
6. What are the most common mistakes students make when solving questions on adding and subtracting integers?
A very common mistake is confusing the rules for signs, especially with subtraction. For example, students often incorrectly calculate `-7 - 4` as `-3` instead of the correct answer, `-11`. Another frequent error is mishandling double negatives, such as in the expression `6 - (-3)`. Practising a variety of important questions helps reinforce the rules and minimises these common errors.
7. What is the difference between the 'opposite' of an integer and its 'absolute value,' and how is this distinction tested in exams?
This is a key conceptual trap. The opposite of an integer is the same number with the opposite sign (e.g., the opposite of -9 is +9). In contrast, the absolute value is an integer's distance from zero, which is always positive (the absolute value of -9 is 9, and the absolute value of +9 is also 9). An exam question might ask you to find the sum of the opposite of -5 and the absolute value of -5, which would be 5 + 5 = 10.
8. Beyond basic calculations, how does mastering Chapter 10 prepare students for more advanced mathematical topics?
Chapter 10 is a critical foundation for future learning. A strong command of integers is essential for understanding topics in Class 7 and beyond, including algebraic expressions (like 3x - 8y), coordinate geometry (plotting points in all four quadrants), and rational numbers. A weak foundation in integers can make these advanced chapters significantly more challenging.