NCERT Solutions for Class 11 Maths Chapter 9 - Straight Lines Exercise 9.3

Exercise 9.3

1. Reduce the following equation into slope-intercept form and find their slopes and the $y$ intercepts.

i. $x  +  7y  =  0$ 

Ans: The equation is $x+7y=0$.

We can write it as $y  =  -  \dfrac{1}{7}  x  +  0$$\ldots (1)$

This equation is of the form $y=mx+c$, where $m=-\dfrac{1}{7}$ and $c=0$ 

Therefore, the equation $\left( 1 \right)$ is the slope-intercept form, where the slope and the y-intercept are $-\dfrac{1}{7}$ and $0$ respectively.

ii. $6x+3y-5=0$ 

Ans: The given equation is $6x+3y-5=0$. 

We can write it as $y=\dfrac{1}{3}(-6x+5)$

$\Rightarrow y=-2x+\dfrac{5}{3}\quad \ldots (1)$

This equation is of the form$\text{y}=\text{mx}+\text{c}$, where $\text{m}=-2$ and$\text{c}=\dfrac{5}{3}$. Therefore, equation $\left( 1 \right)$  in the slope-intercept form, where the slope and the $y$-intercept are $-2$ and $\dfrac{5}{2}$ respectively.

iii. $y=0$

Ans: The given equation is $y=0$. 

We can write it as $y=0.x+0$$.....\left( 1 \right)$

This equation is of the form$y=mx+c$, where $m=0$ and $c=0$. Therefore, equation $\left( 1 \right)$ is in the slope-intercept form, where the slope and the $y$-intercept are \[0\] and \[0\] respectively.

2. Reduce the following equations into intercept form and find their intercepts on the axes.

i. $3x+2y-12=0$

Ans: The given equation is $3x+2y-12=0$.

We can write it as,

$3x+2y=12$

$\Rightarrow \dfrac{3x}{12}+\dfrac{2y}{12}=1$

i.e. $\dfrac{x}{4}+\dfrac{y}{6}-1\quad \ldots (1)$

This equation is of the form$\dfrac{x}{a}+\dfrac{y}{b}=1$, where $a=4$ and$b=6$. 

Therefore, equation (1) is in the intercept form, where the intercepts on the $\text{x}$ and $\text{y}$ axes are $4$ and $6$ respectively.

ii. $4x-3y=6$

Ans:  The given equation is $4x-3y=6$. 

We can write it as,

$\dfrac{4x}{6}-\dfrac{3y}{6}=1$

$\Rightarrow \dfrac{2x}{3}-\dfrac{y}{2}=1$

i.e. $\dfrac{x}{\left( \dfrac{3}{2} \right)}+\dfrac{y}{(-2)}=1$$\ldots (2)$

Therefore, equation $(2)$ is in the intercept form, where the intercepts on $\text{x}$ and $\text{y}$ axes are $\dfrac{3}{2}$ and $-2$ respectively.

iii. $3y+2=0$.

Ans: The given equation is $3\text{y}+2=0$. 

We can write it as $3y=-2$

i.e. $\dfrac{\text{y}}{\left( -\dfrac{2}{3} \right)}=1$$\ldots (3)$

Therefore, equation is in the$\dfrac{x}{a}+\dfrac{y}{b}=1$, where $a=0$ and$b=-\dfrac{2}{3}$. 

Therefore, equation (3) is in the intercept form, where the intercept on the $y$-axis is $-\dfrac{2}{3}$ .

 It has no intercept on the $x$-axis.

3. Find the distance of the points $(-1,1)$ from the line $12(x+6)=5(y-2)$.

Ans: The equation of the line is$12(x+6)=5(y-2)$. 

$\Rightarrow 12x+72=5y-10$

$\Rightarrow 12x-5y+82=0$

Compare the equation $\left( 1 \right)$ with  the general equation of the line $Ax+By+C=0$, we obtain $A=12$, $\text{B}=-5$, and $C=82$.

The perpendicular distance (d) of a line $Ax+By+C=0$ from a point $\left( {{x}_{1}},{{y}_{1}} \right)$ is  

\[\text{d}=\dfrac{\left| \text{A}{{\text{x}}_{1}}+B{{y}_{1}}+\text{C} \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}\]

The given point is$\left( {{x}_{1}},{{y}_{1}} \right)=(-1,1)$. 

So, the distance of the point $(-1,1)$ from the given line

$=\frac{|12(-1)+(-5)(1)+82|}{\sqrt{(12)^{2}+(-5)^{2}}}$ units $=\frac{|-12-5+82|}{\sqrt{169}}$ units $=\frac{|65|}{13}$ units $=5$ units

4. Find the points on the x-axis at what distance from the line $\dfrac{x}{3}+\dfrac{y}{4}=1$ is $4$ units.

Ans: The given equation of the line is $\dfrac{x}{3}+\dfrac{y}{4}=1$

Or $4x+3y-12=0$

Compare the equation (1) with the general equation of the line$Ax+By+C=0$.

We get,

$A=4$,$B=3$, and $C=-12$

Let $(a,0)$ be the point on the x-axis whose distance from the given line is $4$units.

The perpendicular distance $(d)$ of a line $Ax+By+C=0$ from a point $\left( {{x}_{1}},{{y}_{1}} \right)$ is $d=\dfrac{\left| A{{x}_{1}}+B{{y}_{1}}+c \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$

Then $4 = \frac{{\left| {4a + 3 \times 0 - 12} \right|}}{{\sqrt {{4^2} + {3^2}} }}$

$ \Rightarrow {\text{\; }}4 =\frac{{\left| {4a - 12} \right|}}{5}$

$ \Rightarrow {\text{\; }}|4a - 12|= 20$

$ \Rightarrow {\text{\; }} \pm (4a -12) = 20$

$\Rightarrow (4a - 12) = 20$ or $ - (4a - 12) = 20$

$ \Rightarrow 4a = 20 + 12$

or $ - 4a + 12 = 20$

$ \Rightarrow 4a = 32\,or\,\,4a = 12 - 20$

$ \Rightarrow a = \frac{{32}}{4}\,or\,\,a = \frac{{ - 8}}{4}$

$ \Rightarrow a = 8$ or $ - 2$

Thus, the required points on $x$the -axis are $(-2,0)$ and $(8,0)$.

5. Find the distance between parallel lines

i. $15x+8y-34=0$ and $15x+8y+31=0$

Ans: The distance $\left( d \right)$between parallel lines $Ax  +  By  +{{C}_{1}}  =  0$ and $\text{Ax}+\text{By}+{{\text{C}}_{2}}=0$ is$d=\dfrac{\left| {{C}_{1}}-{{C}_{2}} \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$.

The parallel lines are $15x+8y-34=0$ and $15x+8y+31=0$ .

Here, 

$A=15,~\text{B}=8,{{C}_{1}}=-34$, and${{C}_{2}}=31$.

Therefore, the distance between the parallel lines is

\[d  =  \dfrac{\left| {{C}_{1}}  -  {{C}_{2}} \right|}{\sqrt{{{A}^{2}}  +  {{B}^{2}}}}  =  \dfrac{\left| -34  -31 \right|}{\sqrt{{{15}^{2}}  +  {{8}^{2}}}}  \]

\[=  \dfrac{\left| -65 \right|}{\sqrt{289}}  \]Units.

\[=  \dfrac{65}{17}  \]Units.

ii. $l(x+y)+p=0$ and $l(x+y)-r-0$

Ans: The distance $\left( d \right)$between parallel lines $Ax  +  By  +{{C}_{1}}  =  0$ and $\text{Ax}+\text{By}+{{\text{C}}_{2}}=0$ is given by,

$d=\dfrac{\left| {{C}_{1}}-{{C}_{2}} \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$.

The parallel lines are $l(\text{x}+y)+\text{p}=0$ and $l(\text{x}+\text{y})-\text{r}=0$

i.e $lx+ly+p=0$ and $lx+ly-r=0$

Here,

$\text{A}=l ,\text{B}=l,{{C}_{1}}=p$, and ${{C}_{2}}=-{r}$

Therefore, the distance between the parallel lines is

\[d  =  \dfrac{\left| {{C}_{1}}  -  {{C}_{2}} \right|}{\sqrt{{{A}^{2}}  +  {{B}^{2}}}}  =  \dfrac{\left| p  +  r \right|}{\sqrt{{{l}^{2}}  +  {{l}^{2}}}}  \]\[=  \dfrac{\left| p  +  r \right|}{\sqrt{2 {{l}^{2}}}}  \]Units.

\[=  \dfrac{\left| p  +  r \right|}{l\sqrt{ 2}}  \]Units.

\[\Rightarrow d  =  \dfrac{1}{\sqrt{2}}  \dfrac{\left| p  +  r \right|}{l}  \]Units.

6. Find the equation of the line parallel to the line $3x-4y+z=0$ and passing through the point$\left( -  2,3 \right)$.

Ans: The equation of the line is given as,

$3x-4y+2=0$

Or $y  =  \dfrac{3x}{4}  +  \dfrac{2}{4}$

or $y=\dfrac{3}{4}x+\dfrac{1}{2}$ 

Which is of the form $y=mx+c$

$\therefore $ The slope of the given line $=\dfrac{3}{4}$

 It is known that parallel lines have the same slope.

$\therefore $ The slope of the other line $=m=\dfrac{3}{4}$

Equation of line having slope m and passing through $\left( {{x_1},{y_1}} \right)$is given by

$y - {y_1} = m\left( {x - {x_1}} \right)$

Now, the equation of the line that has a slope of $\dfrac{3}{4}$ and passes through the points $(-2,3)$ is

$(y-3)=\dfrac{3}{4}\{x-(-2)\}$

$\Rightarrow 4y-12=3x+6$

i.e ,$3x-4y+18=0$

7. Find the equation of the line perpendicular to the line $x-7y+5=0$ and having $x$ intercept $3$.

Ans: The equation of the line is $x-7y+5=0$.

Or $y=\dfrac{1}{7}x+\dfrac{5}{7}$,

 which is of the form $y=mx+c$

$\therefore $ The slope of the given line $=\dfrac{1}{7}$ .

The slope of the line perpendicular to the line having a slope of $\dfrac{1}{7}$ is $m=-\dfrac{1}{\left( \dfrac{1}{7} \right)}=-7$.

 The equation of the line with slope $-7$ and $x$-intercept 3 is given by $y=m(x-d)$

$\Rightarrow y=-7(x-3)$

$\Rightarrow y=-7x+21$

$\Rightarrow 7x+y=21$

8. Find angles between the lines $\sqrt{3}x+y=1$ and $x+\sqrt{3}y=1$.

Ans: The given lines are $\sqrt{3}x+y=1$ and $x+\sqrt{3}y=1$

$y=-\sqrt{3x}+1 \quad -(1)$  and $y=-\dfrac{1}{\sqrt{3}}x+\dfrac{1}{\sqrt{3}}\quad -(2)$

The slope of the line (1) is ${{m}_{1}}=-\sqrt{3}$, while the slope of the line (2) is ${{m}_{2}}=-\dfrac{1}{\sqrt{3}}$.

The acute angle  between the two lines is given by

$\tan \theta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+m,{{m}_{2}}} \right|$

$\tan \theta =\left| \dfrac{-\sqrt{3}+\dfrac{1}{\sqrt{3}}}{1+(-\sqrt{3})\left( -\dfrac{1}{\sqrt{3}} \right)} \right|$

$\tan \theta =\left| \dfrac{\dfrac{-3+1}{\sqrt{3}}}{1+1} \right|=\left| \dfrac{-2}{2\times \sqrt{3}\mid } \right|$

$\tan \theta =\dfrac{1}{\sqrt{3}}$

$\theta ={{30}^{{}^\circ }}$

Thus, the angle between the given lines is either ${{30}^{{}^\circ }}$ or ${{180}^{*}}-{{30}^{{}^\circ }}={{150}^{{}^\circ }}$.

9. The line through the points $(\text{h},3)$ and $(4,1)$ intersects the line $7\text{x}-9\text{y}-19-0$. At a right angle. Find the value of $\text{h}$.

Ans: The slope of the line passing through points $(\text{h},3)$ and $(4,1)$ is

${m_1} = \frac{{\left( {{y_2} - {y_1}} \right)}}{{\left( {{x_2} - {x_1}} \right)}}\, = \,\frac{{1 - 3}}{{4 - h}} = \frac{{ - 2}}{{4 - h}}$

The slope of the line $7\text{x}-9y-19=0$ or $y=\dfrac{7}{9}x-\dfrac{19}{9}$ is ${{\text{m}}_{2}}=\dfrac{7}{9}$.

It is given that the two lines are perpendicular. 

$\therefore \Rightarrow \text{  }{{m}_{1}}\times {{m}_{2}}=-1$

$\Rightarrow \left( {\frac{{ - 2}}{{4 - h}}} \right) \times \frac{7}{9}$

$\Rightarrow \dfrac{-14}{36-9h}=-1$

$\Rightarrow \text{  }14=36-9h$

$\Rightarrow 9h=36-14$

$\Rightarrow h=\dfrac{22}{9}$

Thus, the value  $h$ is $\dfrac{22}{9}$

10. Prove that the line through the point $\left( {{x}_{1}},{{y}_{1}} \right)$ and parallel to the line $Ax+By+C=0$ is. $A\left( x-{{x}_{1}} \right)+B\left( y-{{y}_{1}} \right)=0$

Ans: The slope of the line $Ax+By+C=0$ or $y=\left( \dfrac{-A}{B} \right)x+\left( \dfrac{-C}{B} \right)$ is $m=-\dfrac{A}{B}$ .

The parallel lines have the same slope.

$\therefore $ The slope of the other line $m=-\dfrac{A}{B}$

The equation of the line passing through a point $\left( {{x}_{1}},{{y}_{1}} \right)$ and having a slope $m=-\dfrac{A}{B}$ is $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$

$y-{{y}_{1}}=-\dfrac{A}{B}\left( x-{{x}_{1}} \right)$

$B\left( y-{{y}_{1}} \right)=-A\left( x-{{x}_{1}} \right)$

$A\left( x-{{x}_{1}} \right)+B\left( y-{{y}_{1}} \right)=0$

Hence, the line through point $\left( {{x}_{1}}-{{y}_{1}} \right)$ and parallel to line $\text{Ax}+\text{By}+C=0$ is $A \left( x-{{x}_{1}} \right)+B\left( y-{{y}_{1}} \right)=0$

 11. Two lines passing through the points $(2,3)$ intersect each other at an angle

 of $60{}^\circ $. If the slope of the one line is $2$, find the equation of the other line.

Ans: It is given that the slope of the first line, ${{m}_{1}}=2$. 

Let the slope of the other line be ${{m}_{2}}$ .

The angle between the two lines is ${{60}^{{}^\circ }}$.

$\therefore \tan 60{}^\circ =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|$

$\Rightarrow \sqrt{3}=\left| \dfrac{2-{{m}_{2}}}{1+2{{m}_{2}}} \right|$

$\Rightarrow \sqrt{3}=\pm \left( \dfrac{2-{{m}_{2}}}{1+2{{m}_{2}}} \right)$

$\Rightarrow \sqrt{3}=\dfrac{2-{{m}_{2}}}{1+2{{m}_{2}}}  \text{or}  \sqrt{3}=-\left( \dfrac{2-{{m}_{3}}}{1+2{{m}_{2}}} \right)$

$\Rightarrow \sqrt{3}\left( 1+2{{m}_{2}} \right)=2-{{m}_{2}}$ or $\sqrt{3}\left( 1+2{{m}_{2}} \right)=-\left( 2-{{m}_{2}} \right)$

\[\Rightarrow \sqrt{3}+2\sqrt{3}{{m}_{2}}+{{\text{m}}_{2}}=2\] or \[\sqrt{3}+2\sqrt{3}{{m}_{2}}-{{m}_{2}}  =  -2\]

$\Rightarrow \sqrt{3}+(2\sqrt{3}+1){{\text{m}}_{2}}=2$or $\sqrt{3}+(2\sqrt{3}-1){{\text{m}}_{3}}=-2$

$\Rightarrow {{m}_{2}}=\dfrac{2-\sqrt{3}}{(2\sqrt{3}+1)}  \text{or}  {{m}_{2}}=\dfrac{-(2+\sqrt{3})}{(2\sqrt{3}-1)}$

Case 1: $\quad {{\text{m}}_{2}}=\left( \dfrac{2-\sqrt{3}}{(2\sqrt{3}+1)} \right)$

The equation of the line passing through the point $(2,3)$ and having a slope of $\dfrac{2-\sqrt{3}}{(2\sqrt{3}+1)}$is 

 $(y-3)=\dfrac{(2-\sqrt{3})}{(2\sqrt{3}+1)}(x-2)$

$(2\sqrt{3}+1)y-3(2\sqrt{3}+1)=(2-\sqrt{3})x-(2-\sqrt{3})2$

$(\sqrt{3}-2)x+(2\sqrt{3}+1)y=-4+2\sqrt{3}+6\sqrt{3}+3$

$(\sqrt{3}-2)x+(2\sqrt{3}+1)y=-1+8\sqrt{3}$

In this case, the equation of the other line is $(\sqrt{3}-2)x+(2\sqrt{3}+1)y=-1+8\sqrt{3}$.

Case 2: $\quad {{\text{m}}_{2}}=\left( \dfrac{-\left( 2+\sqrt{3} \right)}{(2\sqrt{3}-1)} \right)$

The equation of the line passing through the point $(2,3)$ and having a slope of $\left( \dfrac{-\left( 2+\sqrt{3} \right)}{(2\sqrt{3}-1)} \right)$ is 

$(y - 3) = \frac{{ - (2 + \sqrt 3 )}}{{(2\sqrt 3  - 1)}}(x - 2)$

$\left( {2\sqrt 3  - 1} \right)y - \left( {2\sqrt 3  - 1} \right)3 =  - \left( {2 + \sqrt 3 } \right)x + \left( {2 + \sqrt 3 } \right)2$

$\left( {2+ \sqrt 3 } \right)x + \left( {2\sqrt 3 - 1} \right)y = 2\left( {2 + \sqrt 3 } \right) + 3\left( {2\sqrt 3  - 1} \right)$

$\left( {2+ \sqrt 3 } \right)x + \left( {2\sqrt 3 - 1} \right)y = 4 + 2\sqrt 3  +6\sqrt 3  - 3$

$\left( {2 + \sqrt 3 } \right)x + \left( {2\sqrt 3  - 1} \right)y = 1 + 8\sqrt 3 $

In this case, the equation of the other line is$(2+\sqrt{3})x+(2\sqrt{3}-1)y=1+8\sqrt{3}$

The required equation of the line is  $(\sqrt{3}-2)x+(2\sqrt{3}+1)y=-1+8\sqrt{3}$ or $(2+\sqrt{3})x+(2\sqrt{3}-1)y=1+8\sqrt{3}$

12. Find the equation of the right bisector of the line segment joining the points $(3,4)$ and $(-1,2)$.

Ans: The right bisector of a line segment bisects the line segment at $90{}^\circ $.

 The end-point $A(3,4)$ and $B(-1,2)$of the line segment .

Accordingly, the mid-point of $AB=\left( \dfrac{3-1}{2},\dfrac{4+2}{0} \right)-(1,3)$ 

The Slope of $\text{AB}=-\dfrac{2-4}{-1-3}=\dfrac{-2}{-4}=\dfrac{1}{2}$

$\therefore $ The slope of the line perpendicular to $AB=-\dfrac{1}{\left( \dfrac{1}{2} \right)}=-2$ 

The equation of the line passing through $(1,3)$ and having a slope of $-2$ is $(y-3)=-2(x-1)$

$\Rightarrow y-3=-2x+2$

$\Rightarrow 2x+y=5$

Thus, the required equation of the line is $2x+y=5$.

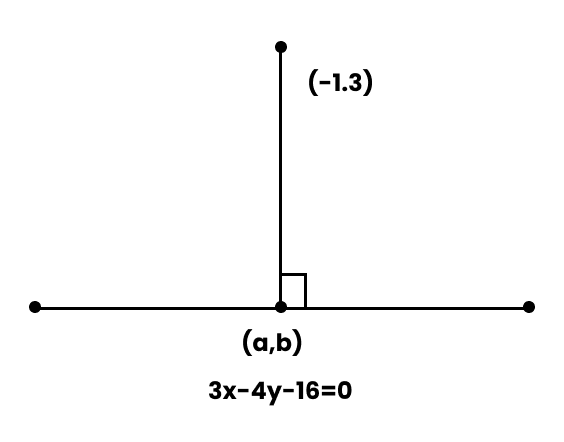
13. Find the coordinates of the foot of the perpendicular from the points $(-1,3)$ to the line $3x-4y-16=0$

Ans: Let $(a,b)$ be the coordinates of the foot of the perpendicular from the points $(-1,3)$ to the line $3x-4y-16=0$.

The slope of the line joining $(-1,3)$ and $(a,b)$, 

$\Rightarrow \text{  }$${{m}_{1}}=\dfrac{b-3}{a+1}$ 

Slope of the line $3x-4y-16=0$ or $y=\dfrac{3}{4}x-4,{{m}_{2}}=\dfrac{3}{4}$ ,

 The above two lines are perpendicular, at, ${{\text{m}}_{1}}{{\text{m}}_{2}}=-1$ 

$\therefore \Rightarrow \text{  }\left( \dfrac{b-3}{a+1} \right)\times \left( \dfrac{3}{4} \right)=-1$

$\Rightarrow \dfrac{3b-9}{4a+4}=-1$

$\Rightarrow 3b-9=-4a-4$

$\Rightarrow 4a+3b=5\quad .....(1)$

The point $(a$, b) lies on the line $3x-4y=16$.

$\therefore \Rightarrow \text{  }3a-4b=16.....(2)$

Solve the equations $(1)$ and (2), we get,

 $a=\dfrac{68}{25}$ and $b=-\dfrac{49}{25}$

Thus, the required coordinates of the foot of the perpendicular are $\left( \dfrac{68}{25},-\dfrac{49}{25} \right)$

14. The perpendicular from the origin to the fine $y=mx+c$ meets it at the point $(-1,2)$. Find the values of $m$ and $c$.

Ans: The  equation of the line is $y=mx+c$. 

The perpendicular from the origin meets the given line at $(-1,2)$. 

So, the line joining the points $(0,0)$ and $(-1,2)$ is perpendicular to the given line. 

$\therefore $ The slope of the line joining $(0,0)$ and $(-1,2)=\dfrac{2}{-1}=-2$ The slope of the given line is $\text{m}$.

 $\therefore \text{m}\times -2=-1\quad $     The two  lines are perpendicular

$\Rightarrow m=\dfrac{1}{2}$.

The  points $(-1,2)$ lie on the given line, it satisfies the equation $y=mx+c$

$\therefore 2=\text{m}(-1)+c$

$\Rightarrow 2=2+\dfrac{1}{2}(-1)+c$

 $\Rightarrow c=2+\dfrac{1}{2}=\dfrac{5}{2}$

The respective values of $\text{m}$ and $\text{c}$ are $\dfrac{1}{2}$ and $\dfrac{5}{2}$.

15. If $p$ and $q$ are the lengths of the perpendicular from the origin to the lines $x\cos \theta -y\sin \theta =k$ $\cos 2\theta $ and $\text{x}\sec \theta +y$ cosec $\theta =\text{k}$, respectively, prove that ${{p}^{2}}+4{{q}^{2}}-{{k}^{2}}$

Ans: The equation of lines are $x\cos \theta -y\sin \theta =k\cos 2\theta \quad \ldots (1) $

$x\sec \theta +y$ cases $\theta =k\quad \ldots (2)$

The perpendicular distance (d) of a line $Ax+By+C=0$ from a point $\left( {{x}_{1}},{{x}_{2}} \right)$ is given by $d=\dfrac{\left| A{{x}_{1}}+B{{y}_{1}}+c \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$

Compare the  equation $\left( 1 \right)$  the general equation of line 

ie., $Ax+By+C=0$, we obtain $A=\cos \theta $ ,$B=\sin \theta $, and $C=k\cos 2\theta $.

$\text{p}$ is the length of the perpendicular from $(0,0)$ to line $\left( 1 \right)$. \[\therefore p=\dfrac{|A(0)+B(0)+C|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}=\dfrac{|C|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}\]

$\therefore p=\dfrac{|-k\cos 2\theta |}{\sqrt{{{\cos }^{2}}\theta +{{\sin }^{2}}\theta }}=|-k\cos 2\theta |\quad \ldots (3)$

 Compare the  equation (2) to the general equation of line ie., $Ax+By+C=0$, we obtain $A=\sec \theta $ , $B=\operatorname {cosec} \theta $, and $C=-k$

It is given that $q$ is the length of the perpendicular from $(0,0)$ to line (2). 

$\therefore \mathrm{q}=\frac{|\mathrm{A}(\mathrm{O})+\mathrm{B}(\mathrm{O})+\mathrm{C}|}{\sqrt{\mathrm{A}^{2}+\mathrm{B}^{2}}}=\frac{|\mathrm{C}|}{\sqrt{\mathrm{A}^{2}+\mathrm{B}^{2}}}=\frac{|-\mathrm{k}|}{\sqrt{\sec ^{2} \theta+\operatorname{cosec}^{2} \theta}}$

From (3) and (4), we have

$p^{2}+4 q^{2}-(|-k \cos 2 \theta|)^{2}+4\left(\frac{|-k|}{\sqrt{\sec ^{2} \theta+\operatorname{cosec}^{2} \theta}}\right)^{2}$

$=k^{2} \cos ^{2} 2 \theta+\frac{4 k^{2}}{\left(\sec ^{2} \theta+\operatorname{cosec}^{2} \theta\right)}$

$=k^{2} \cos ^{2} 2 \theta+\frac{4 k^{2}}{\left(\frac{1}{\cos ^{2} \theta}+\frac{1}{\sin ^{2} \theta}\right)}$

$=k^{2} \cos ^{2} 2 \theta+\frac{4 k^{2}}{\left(\frac{\sin ^{2} \theta+\cos ^{2} \theta}{\sin ^{2} \theta \cos ^{2} \theta}\right)}$

$=k^{2} \cos ^{2} 2 \theta+\frac{4 k^{2}}{\left(\frac{1}{\sin ^{2} \theta \cos ^{2} \theta}\right)}$

$=k^{2} \cos ^{2} 2 \theta+4 k^{2} \sin ^{2} \theta \cos ^{2} \theta$

$=k^{2} \cos ^{2} 2 \theta+k^{2}(2 \sin \theta \cos \theta)^{2}$

$=k^{2} \cos ^{2} 2 \theta+k^{2} \sin ^{2} 2 \theta$

$=k^{2}\left(\cos ^{2} 2 \theta+\sin ^{2} 2 \theta\right)$

$=\mathbf{k}^{2}$

Hence, vre proved that $\mathrm{p}^{2}+4 \mathrm{q}^{2}=\mathrm{k}^{2}$

16. In the triangle $\text{ABC}$ with vertices $\text{A}(2,3),\text{B}(4,-1)$ and $\text{C}(1,2)$, find the equation and length of altitude from the vertex $A$.

Ans: Let $\text{AD}$ be the altitude of the triangle $\text{ABC}$ from the vertex $\text{A}$. 

 $\Rightarrow \text{  }AD\bot BC$,

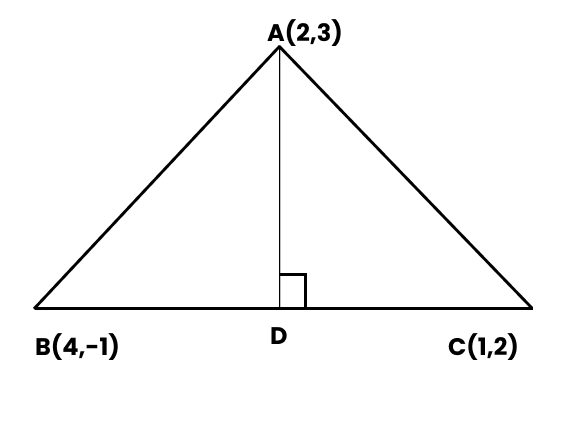
The slope of the line BC $\dfrac[21][1-4]$=$-1$

Therefore slope of line AD  $= \dfrac{-1}{-1}$=$1$

The equation of the line AD passing through the point $A (2,3)$ and having a slope $1$ is $(y-3)=1(x-2)$

$\Rightarrow x-y+1=0$

$\Rightarrow y-x=1$

Therefore, equation of the altitude from a vertex$A=y-x=1$.

Length of $AD=$ Length of the perpendicular from A $(2,3)$ to$BC$.

The equation of $\text{BC}$ is 

$(y+1)=\dfrac{2+1}{1-4}(x-4)$

$\Rightarrow \text{  }(y+1)=-1(x-4)$

$\Rightarrow y+1=-x+4$

$\Rightarrow x+y-3=0$$\ldots (1)$

The perpendicular distance $(d)$ of a line $Ax+By+C=0$ from a point $\left( {{x}_{1}},{{y}_{1}} \right)$ is $d=\dfrac{\left| A{{x}_{1}}+B{{y}_{1}}+c \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$

 Compare the equation $(1)$ to the general equation of the line$Ax+By+C=0$.

We get,

 $A=1$,$\text{B}=1$ and $C=-3$

Length of AD $=  \dfrac{\left| 1\times 2+1\times 3-3 \right|}{\sqrt{{{1}^{2}}+{{1}^{2}}}}$ units 

$=\dfrac{\left| 2 \right|}{\sqrt{2}}$units $=\sqrt{2 }$units.

Length of AD $=\sqrt{2 }$units.

Thus, the equation and length of the altitude from vertex $A$ are $y-x=1$ and $\sqrt{2}$ wits respectively.

17. If $\text{p}$ is the length of the perpendicular from the origin to the line whose intercepts on the axes are $a$, and $\text{b}$, then show that $\dfrac{1}{{{p}^{2}}}=\dfrac{1}{{{a}^{2}}}+\dfrac{1}{{{b}^{2}}}$.

Ans: The equation of a line whose intercepts on the axes are $a$ and $\text{b}$ is $\dfrac{x}{a}+\dfrac{y}{b}=1$

$\text{bx}+ay=\text{ab}$

Or $bx+ay-ab=0$

The perpendicular distance $(d)$ of a line $Ax+By+C=0$ from a point $\left( {{x}_{1}},{{y}_{1}} \right)$ is $d=\dfrac{\left| A{{x}_{1}}+B{{y}_{1}}+c \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$

Compare the equation $(1)$ with the general equation of the line$Ax+By+C=0$, 

We obtain$A=b$,$\text{B}=a$ and $C=-ab$

Therefore, if $p$ is the length of the perpendicular from a point $\left( {{x}_{1}},{{y}_{1}} \right)=(0,0)$ to lime$\left( 1 \right)$. We obtain $p  =  \dfrac{\left| A\left( 0 \right)  +  B\left( 0 \right)  -  ab \right|}{\sqrt{{{b}^{2}}+{{a}^{2}}}}$

$\Rightarrow p=\dfrac{|-ab|}{\sqrt{{{b}^{2}}+{{a}^{2}}}}$.

Square both sides, 

We get

$\Rightarrow \text{  }{{p}^{2}}  =  \dfrac{{{\left( -  ab \right)}^{2}}}{{{a}^{2}}  +  {{b}^{2}}}$

$\Rightarrow \text{  }{{p}^{2}}\left( {{a}^{2}}  +  {{b}^{2}} \right)  =  {{a}^{2}}{{b}^{2}}$

$\Rightarrow \text{  }\dfrac{{{a}^{2}}  +  {{b}^{2}}}{{{a}^{2}}{{b}^{2}}}  =  \dfrac{1}{{{p}^{2}}}$

$\Rightarrow \text{  }\dfrac{1}{{{p}^{2}}}  =  \dfrac{1}{{{a}^{2}}}  +  \dfrac{1}{{{b}^{2}}}$

Hence proved that  $\dfrac{1}{{{p}^{2}}}=\dfrac{1}{{{a}^{2}}}+\dfrac{1}{{{b}^{2}}}$

Conclusion

Ex 9.3 Class 11 Maths NCERT Solutions has provided an in-depth understanding of several advanced concepts related to straight lines. You have learned how to calculate the distance of a point from a line, the distance between two parallel lines, and the angle between two intersecting lines. By understanding these topics covered in class 11 ex 9.3, you have enhanced your ability to solve complex geometric problems and gained a deeper appreciation for the properties of lines in coordinate geometry.

Class 11 Maths Chapter 9: Exercises Breakdown

CBSE Class 11 Maths Chapter 9 Other Study Materials

Chapter-Specific NCERT Solutions for Class 11 Maths

Given below are the chapter-wise NCERT Solutions for Class 11 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Important Related Links for CBSE Class 11 Maths