NCERT Exemplar for Class 9 Maths Chapter 5 - Introduction to Euclids Geometry (Book Solutions)

Multiple Choice Questions:

Sample Question 1: Euclid’s second axiom (as per order given in the Textbook for Class IX) is -

(A) The things which are equal to the same thing are equal to one another.

(B) If equals be added to equals, the wholes are equal.

(C) If equals be subtracted from equals, the remainder are equals.

(D) Things which coincide with one another are equal to one another.

Ans: The correct answer is (B).

Euclid's second axiom states that, “if equals are added to equals, then the wholes are equal.”

Sample Question 2: Euclid’s fifth postulate is

(A) The whole is greater than the part.

(B) A circle may be described with any center and any radius.

(C) All right angles are equal to one another.

(D) If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.

Ans: The correct answer is (D).

Euclid’s fifth postulate states that, “if a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.”

Sample Question 3: The things which are double of the same thing are

(A) equal

(B) unequal

(C) halves of the same thing

(D) double of the same thing

Ans: The correct answer is (A).

According to Euclid's sixth axiom, “things which are double of the same thing are equal to one another.”

Sample Question 4: Axioms are assumed

(A) universal truths in all branches of mathematics

(B) universal truths specific to geometry

(C) theorems

(D) definitions

Ans: The correct answer is (A).

Axioms are those believed truths which are accepted without any proof. They are used to build a foundation for a concept. Therefore, axioms are assumed to be universal truths in all branches of mathematics.

Sample Question 5: John is of the same age as Mohan. Ram is also of the same age as Mohan. State the Euclid’s axiom that illustrates the relative ages of John and Ram.

(A) First Axiom

(B) Second Axiom

(C) Third Axiom

(D) Fourth Axiom

Ans: The correct answer is (A).

In the above given problem, we can use the first axiom of Euclid which states that, “the things which are equal to the same thing are equal to one another.” Here, the ages of John and Ram are equal to the age of Mohan, so the ages of John and Ram are equal.

Sample Question 6: If a straight line falling on two straight lines makes the interior angles on the same side of it, whose sum is 120°, then the two straight lines, if produced indefinitely, meet on the side on which the sum of angles is

(A) less than 120°

(B) greater than 120°

(C) is equal to 120°

(D) greater than 180°

Ans: The correct answer is (C).

According to the fifth postulate given by Euclid, it states that,”if a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.” Here, the sum of interior angles is less than two right angles i.e. 180° so the two lines will meet on the side on which the sum of angles is 120°.

Exercise 5.1

1. The three steps from solids to points are:

(A) Solids - surfaces - lines – points

(B) Solids - lines - surfaces – points

(C) Lines - points - surfaces – solids

(D) Lines - surfaces - points solids

Ans: (A) is the correct answer.

There are three steps going from solids to points, which are as follows: solids-surface-lines-points.

2. The number of dimensions, a solid has:

(A) 1

(B) 2

(C) 3

(D) 0

Ans: (C) is the correct answer.

The solids have some particular lengths, widths and heights. Therefore, all solids have three dimensions. For example: a cone, cuboid, cube, cylinder, prism ,etc.

3. The number of dimensions, a surface has:

(A) 1

(B) 2

(C) 3

(D) 0

Ans: (B) is the correct answer.

A surface has a finite length and width but has no depth or height. Therefore a surface has 2 dimensions.

4. The number of dimension, a point has:

(A) 0

(B) 1

(C) 2

(D) 3

Ans: (A) is the correct answer.

A point has no measurements such as the length, width or height. Hence, a point is dimensionless and has no dimension.

5. Euclid divided his famous treatise “The Elements” into:

(A) 13 chapters

(B) 12 chapters

(C) 11 chapters

(D) 9 chapters

Ans: (A) is the correct answer.

Euclid’s famous treatise “The Elements” was divided into 13 chapters.

6. The total number of propositions in the Elements are:

(A) 465

(B) 460

(C) 13

(D) 55

Ans: (A) is the correct answer.

A proposition, which is also known as theorems, are such statements whose proof can be given. Euclid gave a total of 465 propositions which were divided into his 13 chapters.

7. Boundaries of solids are:

(A) surfaces

(B) curves

(C) lines

(D) points

Ans: (A) is the correct answer.

The boundaries of solids are represented as surfaces.

8. Boundaries of surfaces are:

(A) surfaces

(B) curves

(C) lines

(D) points

Ans: (B) is the correct answer.

The boundaries of surfaces are represented as curves.

9. In Indus Valley Civilisation (about 3000 B.C.), the bricks used for construction work were having dimensions in the ratio

(A) 1 : 3 : 4

(B) 4 : 2 : 1

(C) 4 : 4 : 1

(D) 4 : 3 : 2

Ans: (B) is the correct answer.

The bricks used for the construction work in the Indus Valley Civilisation were having their dimensions in the ratio of 4 : 2 : 1.

10. A pyramid is a solid figure, the base of which is

(A) only a triangle

(B) only a square

(C) only a rectangle

(D) any polygon

Ans: (D) is the correct answer.

A pyramid is a solid figure whose base can be a triangle, square, rectangle or some other polygon as well. 

11. The side faces of a pyramid are:

(A) Triangles

(B) Squares

(C) Polygons

(D) Trapeziums

Ans: (A) is the correct answer.

The faces of the sides of a pyramid are all triangles. However, the shape of the base can be any polygon such as a triangle, square or any other polygon.

12. It is known that if \[x{\text{ }} + {\text{ }}y{\text{ }} = {\text{ }}10\] then \[x{\text{ }} + {\text{ }}y{\text{ }} + {\text{ }}z{\text{ }} = {\text{ }}10{\text{ }} + {\text{ }}z\] . The Euclid’s axiom that illustrates this statement is:

(A) First Axiom

(B) Second Axiom

(C) Third Axiom

(D) Fourth Axiom

Ans: (B) is the correct answer.

It is given that if \[x{\text{ }} + {\text{ }}y{\text{ }} = {\text{ }}10\] , then it implies that \[x{\text{ }} + {\text{ }}y{\text{ }} + {\text{ }}z{\text{ }} = {\text{ }}10{\text{ }} + {\text{ }}z\] . The most accurate Euclid’s axiom that illustrates this statement is the second axiom which states that “if equals are added to equals, then the wholes are equal.”

13. In ancient India, the shapes of altars used for household rituals were:

(A) Squares and circles

(B) Triangles and rectangles

(C) Trapeziums and pyramids

(D) Rectangles and squares

Ans: (A) is the correct answer.

In ancient India, the most common shapes of the altars used for household and communal rituals were squares and circles. Vedic rites, such as the yagna, were performed using the altars constructed in squared and circular shapes.

14. The number of interwoven isosceles triangles in Sriyantra (in the Atharva Veda) is:

(A) Seven

(B) Eight

(C) Nine

(D) Eleven

Ans: (C) is the correct answer.

In the ancient Atharva Veda, the Sriyantra consists of a number of nine interwoven isosceles triangles. The Sriyantra is a kind of mystical diagram which is known as a yantra. It contains nine interlocking isosceles triangles which radiate out from a central point.

15. Greek’s emphasized on:

(A) Inductive reasoning

(B) Deductive reasoning

(C) Both A and B

(D) Practical use of geometry

Ans: (B) is the correct answer.

The Greeks used deductive reasoning to establish the truth of the statements that they discovered. The Greeks used to emphasize the study of Greek philosophy and Greek history of mathematics and logic. Its first known proof was given by a Greek mathematician, Thales.

16. In Ancient India, Altars with combination of shapes like rectangles, triangles and trapeziums were used for:

(A) Public worship

(B) Household rituals

(C) Both A and B

(D) None of A, B, C

Ans: (A) is the correct answer.

In Ancient India the Altars which were made with the combination of shapes like rectangles, triangles and trapeziums were used for public worship. Whereas the Altars made up of shapes like the square and circle, were used for the household rituals.

17. Euclid belongs to the country:

(A) Babylonia

(B) Egypt

(C) Greece

(D) India

Ans: (C) is the correct answer.

Euclid was born in the early 300 B.C. He was a Greek mathematician who is best known for his treatise on geometry, the Elements.

18. Thales belongs to the country:

(A) Babylonia

(B) Egypt

(C) Greece

(D) Rome

Ans: (C) is the correct answer.

Thales was born in the 625 B.C. He was a Greek mathematician, astronomer and pre-Socratic philosopher who is best known for giving the first known proof of his deductive reasoning.

19. Pythagoras was a student of:

(A) Thales

(B) Euclid

(C) Both A and B

(D) Archimedes

Ans: (A) is the correct answer.

Pythagoras was a Greek mathematician who was born in 572 B.C. Pythagoras was a student of another Greek mathematician Thales.

20. Which of the following needs a proof?

(A) Theorem

(B) Axiom

(C) Definition

(D) Postulate

Ans: (A) is the correct answer.

Theorems are the statements which need to be proven, or can be proved.

21. Euclid stated that all right angles are equal to each other in the form of

(A) an axiom

(B) a definition

(C) a postulate

(D) a proof

Ans: (C) is the correct answer.

Euclid’s fourth postulate states that all right angles are equal to each other. Postulates are statements which are accepted as truth and used as the basis for an argument or theory. Postulates are those true assumptions that are specific to geometry.

22. ‘Lines are parallel if they do not intersect’ is stated in the form of

(A) an axiom

(B) a definition

(C) a postulate

(D) a proof

Ans: (B) is the correct answer.

Since two parallel lines are defined as a pair of lines which do not intersect. Therefore, ‘Lines are parallel if they do not intersect’ is the form of a definition.

Short Answer Questions with Reasoning:

Sample Question 1. : Write whether the following statements are True or False? Justify your answer.

(i) Pyramid is a solid figure, the base of which is a triangle or square or some other polygon and its side faces are equilateral triangles that converge to a point at the top.

Ans: False. 

Pyramids are solid structures with triangular or square bases while having sides made of triangles having a common vertex at the top, but they need not necessarily be equilateral triangles.

(ii) In Vedic period, squares and circular shaped altars were used for household rituals, while altars whose shapes were combinations of rectangles, triangles and trapeziums were used for public worship.

Ans: True. 

The square and circular shaped altars were used for household rituals whereas rectangular, triangular and trapezium shaped altars were used for the public worship during the Vedic period.

(iii) In geometry, we take a point, a line and a plane as undefined terms.

Ans: True. 

The concept of a point, a line and a plane exists without a proper definition and hence they are considered to be undefined terms.

(iv) If the area of a triangle equals the area of a rectangle and the area of the rectangle equals that of a square, then the area of the triangle also equals the area of the square.

Ans: True. 

According to Euclid’s first axiom,” the things which are equal to the same thing are equal to one another.” Therefore, if the areas of a triangle and a rectangle are equal to the area of a square, then the area of the triangle is equal to the area of the square.

(v) Euclid’s fourth axiom says that everything equals itself.

Ans: True.

 According to Euclid’s fourth axiom,”things which coincide with one another are equal to one another.” Therefore, since everything coincides with itself, hence everything is equal to itself.

(vi) The Euclidean geometry is valid only for figures in the plane.

Ans: True. 

The Euclidean geometry is valid only for plane figures in two dimensional space and it fails for the curved surfaces or in multidimensional spaces.

Exercise 5.2

Write whether the following statements are True or False? Justify your answer:

1. Euclidean geometry is valid only for curved surfaces.

Ans: False. 

Euclidean geometry is valid for both, the surfaces of curves as well as the straight lines.

2. The boundaries of the solids are curves.

Ans: False. 

The boundaries of solid structures are surfaces whereas curves are the boundaries of surfaces.

3. The edges of a surface are curves.

Ans: True. 

The edges of surfaces are curves. For example, the edges of a circular surface are a curve. The curve can also be a straight line for a square, triangle, etc.

4. The things which are double of the same thing are equal to one another.

Ans: True. 

Euclid’s sixth axiom states that, “The things which are double of the same thing are equal to one another.” Mathematically, if \[a = 2c\] and \[b = 2c\] then it implies that \[a = b = 2c\] .

5. If a quantity B is a part of another quantity A, then A can be written as the sum of B and some third quantity C.

Ans: True. 

Since the fifth axiom of Euclid states that the whole is greater than the part. Hence, if A is whole and B is its part then there is some other part remaining which can be represented as C. In that way, A coincides with the sum of B and C. Now by Euclid’s fourth axiom, things which coincide with one another are equal to one another. Therefore A can be written as \[A = B + C\] .

6. The statements that are proved are called axioms.

Ans: False. 

The statements which are proved are called theorems whereas axioms are true assumptions which are used throughout a theory. Axioms are considered true so as to form a basis for a theory to use afterwards.

7. “For every line l and for every point P not lying on a given line l, there exists a unique line m passing through P and parallel to l” is known as Playfair’s axiom.

Ans: True. 

The given statement is true, because it is similar to the Euclid’s fifth postulate of two parallel lines. If a line m is drawn from the point P which does not intersect the line l, then by the definition of parallel lines, the lines l and m are parallel.

8. Two distinct intersecting lines cannot be parallel to the same line.

Ans: True.

The given statement is true, because it is similar to the Euclid’s fifth postulate of two parallel lines. If two distinct lines are intersecting then they are non-parallel lines. Hence, two non-parallel lines can not be parallel to the same lines otherwise they will be parallel to each other which would be a contradiction.

9. Attempts to prove Euclid’s fifth postulate using the other postulates and axioms led to the discovery of several other geometries.

Ans: True. 

The fifth postulate of Euclid states that if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, then if these two straight lines are produced indefinitely, they will meet on that side on which the angles are less than the two right angles.

The given statement is true because those other geometries were different from Euclidean geometry and therefore were called non-Euclidean geometry.

Short Answer Questions:

Sample Question 1: Ram and Ravi have the same weight. If they each gain weight by 2 kg, how will their new weights be compared ?

Ans: Given that, Ram and Ravi have the same weight. Now by Euclid’s second axiom,”if equals are added to equals, then the holes are equal.” Hence, if they each gain weight by 2kg then their new gained weights will also be equal.

Sample Question 2: Solve the equation a – 15 = 25 and state which axiom do you use here.

Ans:  Euclid’s second axiom states that,”if equals are added to equals, then the wholes are equal.” Now, if we add 15 to both sides of the equation a – 15 = 25 then we will get a – 15 + 15 = 25 + 15.

Therefore, that gives us a = 40 .

Sample Question 3: In the Fig. 5.1, if ∠1 = ∠3, ∠2 = ∠4 and ∠3 = ∠4, write the relation between ∠1 and ∠2, using an Euclid’s axiom.

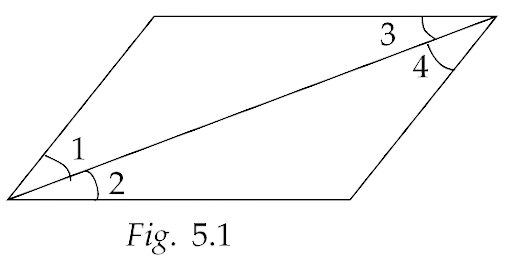
Ans: In the above figure, we are given that, ∠1 = ∠3, ∠2 = ∠4 and ∠3 = ∠4.

Now, according to Euclid’s first axiom, which states that,”things which are equal to the same thing are equal to one another.”

Since ∠1 = ∠3, and ∠3 = ∠4, hence that gives us ∠1 = ∠4.

Now that ∠1 = ∠4 and also ∠2 = ∠4, therefore ∠1 = ∠2.

Sample Question 4: In Fig. 5.2, we have : AC = XD, C is the midpoint of AB and D is the midpoint of XY. Using an Euclid’s axiom, show that AB = XY.

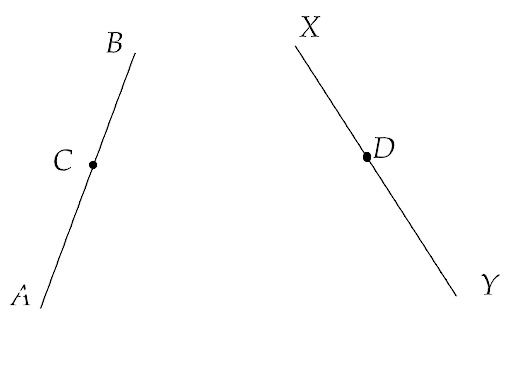
Ans: Given that, AC = XD and C and D are the midpoints of AB and XY respectively.

Now since AC = XD, multiplying both sides by 2 gives us 2AC = 2XD

According to Euclid’s sixth axiom,”things which are double of the same thing are equal to one another.”

Therefore, we get AB = XY.

Exercise 5.3

Solve each of the following question using appropriate Euclid’ s axiom:

1. Two salesmen make equal sales during the month of August. In September, each salesman doubles his sales for the month of August. Compare their sales in September.

Ans: Given that, two salesmen make equal sales during the month of August.

Let the sales of the two given salesmen for the month of August be \[x\] and \[y\] respectively.

Since they make equal sales during the month of August,

Hence we have,

\[ \Rightarrow x = y\] 

Now in September, both salesmen double their sales of the month of August.

Therefore, the sales of both salesmen in September would be \[2x\] and \[2y\] respectively.

Now, by Euclid's axiom, we have “things which are double of the same things are equal to one another.”

\[ \Rightarrow 2x = 2y\]

Therefore, the two salesmen make equal sales in the month of September.

2. It is known that \[x{\text{ }} + {\text{ }}y{\text{ }} = {\text{ }}10\] and that \[x{\text{ }} = {\text{ }}z\] . Show that \[z{\text{ }} + {\text{ }}y = {\text{ }}10\] ?

Ans: It is given that

\[ \Rightarrow x{\text{ }} + {\text{ }}y{\text{ }} = {\text{ }}10\]

And

\[ \Rightarrow x{\text{ }} = {\text{ }}z\]

Now by Euclid’s second axiom, we have, “if equals are added to equals, the wholes are equal.”

\[ \Rightarrow x{\text{ }} + {\text{ }}y{\text{ }} = {\text{ }}z + y\]

Therefore, we have

\[ \Rightarrow z{\text{ }} + {\text{ }}y{\text{ }} = {\text{ }}10\]

3. Look at the figure, and show that Length AH > sum of lengths of AB + BC + CD.

Ans: In the given figure, we can see that the lengths AB, BC and CD are parts of line segment AH.

Now since, we have

\[\; \Rightarrow AB + BC + CD = AD\;\]    …(1)

Also, AD is a part of line AH.

Therefore, by Euclid’s fifth axiom, we have “the whole is greater than the part.”

 Hence, we can write

\[ \Rightarrow AH > AD\]

That gives,

\[\; \Rightarrow AH > AB + BC + CD\;\]

Therefore, Length AH > sum of lengths of AB + BC + CD.

4. In Fig.5.4, we have AB = BC, BX = BY. Show that AX = CY.

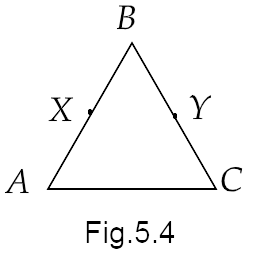
Ans: We are given that,

\[ \Rightarrow AB = BC\]    …(1)

And

\[ \Rightarrow BX = BY\]    …(2)

Now, if we subtract the equation (2) from the equation (1), then we get

\[ \Rightarrow AB - BX = BC - BY\]

Now using Euclid’s third axiom, we have “if equals are subtracted from equals, the remainders are equal”.

Hence, we have

\[ \Rightarrow AX = CY\]

5. In Fig.5.5, we have X and Y as the mid-points of AC and BC and AX = CY. Show that AC = BC.

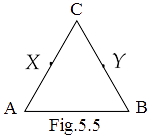
Ans: Given that, X and Y are the mid points of the sides AC and BC of the triangle ABC and,

\[ \Rightarrow AX = CY\]

Multiplying both sides of this equation by 2, we get

\[ \Rightarrow 2AX = 2CY\]

Now by Euclid’s sixth axiom, we have, “things which are double of the same thing are equal to one another.”

Therefore, we can write

\[ \Rightarrow AC = BC\]

6. In Fig.5.6, we have \[BX = \dfrac{1}{2}AB\] \[BY = \dfrac{1}{2}BC\] and AB = BC. Show that BX = BY.

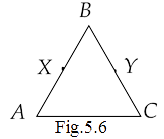
Ans: In the triangle ABC, we are given that,

\[ \Rightarrow AB = BC\]

Now using Euclid’s seventh axiom, we have “things which are halves of the same things are equal to one another.”

Therefore, we have

\[ \Rightarrow \dfrac{1}{2}AB = \dfrac{1}{2}BC\]

But it is given that \[BX = \dfrac{1}{2}AB\] and \[BY = \dfrac{1}{2}BC\]

Therefore,

\[ \Rightarrow BX = BY\]

7.In the given figure, we have \[\angle 1 = \angle 2\] , \[\angle 2 = \angle 3\] . Show that \[\angle 1 = \angle 3\] .

Ans: In the above question, we are given that,

\[ \Rightarrow \angle 1 = \angle 2\]

And

\[ \Rightarrow \angle 2 = \angle 3\]

Now using Euclid’s first axiom, we have “things which are equal to the same thing are equal to one other.”

Therefore, we can write

\[ \Rightarrow \angle 1 = \angle 3\]

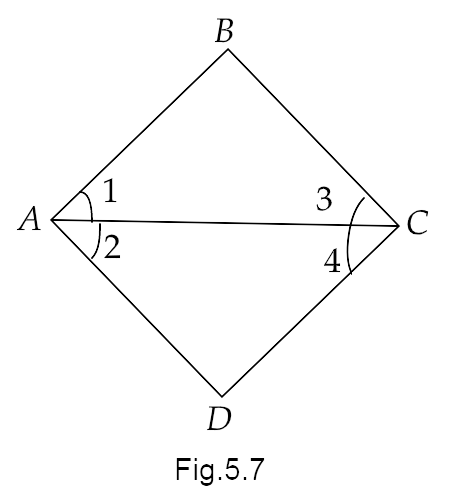
8. In the given figure, we have \[\angle 1 = \angle 3\] and \[\angle 2 = \angle 4\] . Show that \[\angle A = \angle C\] .

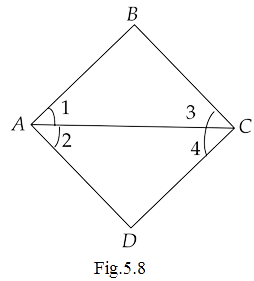
Ans: In the above figure, we are given that \[\angle 1 = \angle 3\] and \[\angle 2 = \angle 4\] .

From the figure, we can write

\[ \Rightarrow \angle A = \angle 1 + \angle 2\]

And

\[ \Rightarrow \angle C = \angle 3 + \angle 4\]

Now using Euclid’s second axiom, we have “if equal are added to equals, the whole are equal.”

Therefore,

\[ \Rightarrow \angle 1 + \angle 2 = \angle 3 + \angle 4\]

That gives us,

\[ \Rightarrow \angle A = \angle C\]

9. In the given figure, we have \[\angle ABC = \angle ACB\] , \[\angle 4 = \angle 3\]. Show that \[\angle 1 = \angle 2\] .

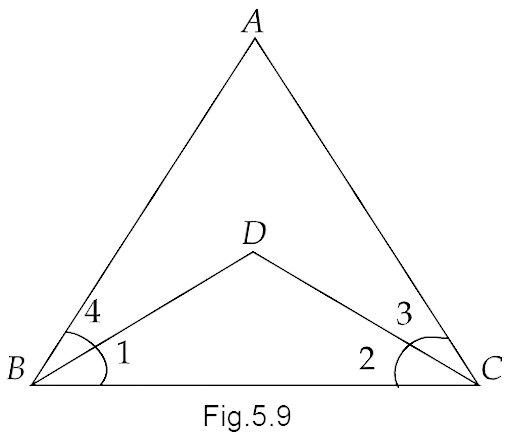
Ans: Given that, 

\[ \Rightarrow \angle ABC = \angle ACB\]

And

\[ \Rightarrow \angle 4 = \angle 3\]

Now using Euclid’s third axiom, we have “if equals are subtracted from equals, the remainders are equal.”

Therefore, subtracting these equations gives us,

\[ \Rightarrow \angle ABC - \angle 4 = \angle ACB - \angle 3\]

Hence, we have

\[ \Rightarrow \angle 1 = \angle 2\]

10. In the Fig. 5.10, we have AC = DC, CB = CE. Show that AB = DE.

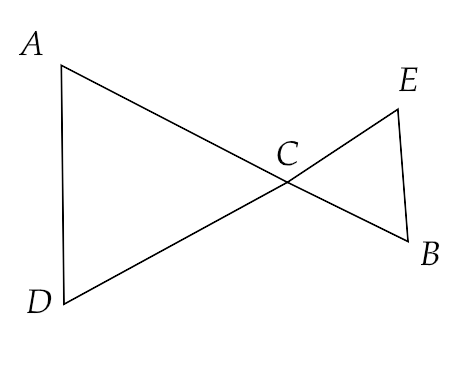
Ans: In the above figure 5.10, we are given that

\[ \Rightarrow AC = DC\]

And

\[ \Rightarrow CB = CE\]

Now from Euclid's second axiom, we know that “if equals are added to equals, the wholes are equal.”

Therefore after adding the above two equations, we have

\[ \Rightarrow AC + CB = DC + CE\]

That gives us,

\[ \Rightarrow AB = DE\]

11. In the given figure, if \[OX = \dfrac{1}{2}XY\] , \[PX = \dfrac{1}{2}XZ\] and OX = PX, show that XY = XZ.

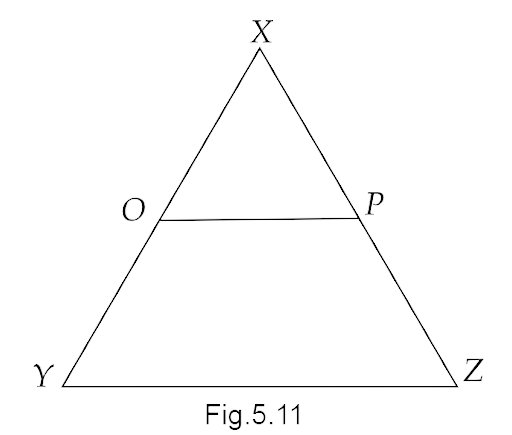
Ans: In the above given figure, we have

\[ \Rightarrow OX = PX\]

Now, it is also given that,

\[ \Rightarrow OX = \dfrac{1}{2}XY\]

And,

\[ \Rightarrow PX = \dfrac{1}{2}XZ\]

Now using Euclid’s seventh axiom, we have ” Things which are halves of the same thing are equal to one another.”

Therefore, we can write

\[ \Rightarrow \dfrac{1}{2}XY = \dfrac{1}{2}XZ\]

Now again using Euclid’s sixth axiom, we have “Things which are double of the same thing are equal to one another.”

Therefore, we have

\[ \Rightarrow XY = XZ\]

12. In the Fig.5.12:

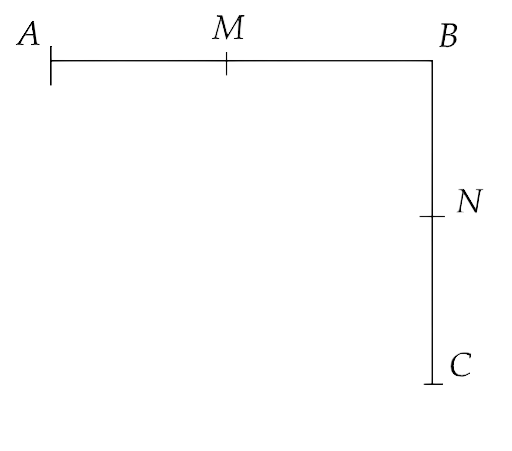
(i) AB = BC, M is the midpoint of AB and N is the mid- point of BC. Show that AM = NC.

Ans: In the above given figure we have,

\[ \Rightarrow AB = BC\]

Given that, M and N are the mid-points of AB and BC respectively.

That gives us,

\[ \Rightarrow AM = MB = \dfrac{1}{2}AB\]

And,

\[ \Rightarrow BN = NC = \dfrac{1}{2}BC\]

Now, using Euclid’s seventh axiom, we have “Things which are halves of the same thing are equal to one another.”

Therefore, we have

\[ \Rightarrow \dfrac{1}{2}AB = \dfrac{1}{2}BC\]

That gives us,

\[ \Rightarrow AM = NC\]

(ii) BM = BN, M is the midpoint of AB and N is the midpoint of BC. Show that AB = BC.

Ans: In the above given figure we have,

\[ \Rightarrow BN = BM\]

Given that, , M and N are the mid-points of AB and BC respectively.

That gives us,

\[ \Rightarrow AM = BM = \dfrac{1}{2}AB\]

And,

\[ \Rightarrow BN = CN = \dfrac{1}{2}BC\]

Now since \[BN = BM\] , therefore multiplying both sides by 2 we have

\[ \Rightarrow 2BM = 2BN\]

Now by using Euclid’s sixth axiom, we have “Things which are double of the same thing are equal to one another.”

Therefore, we have

\[ \Rightarrow AB = BC\]

Long Answer Questions:

Sample Question 1: Read the following statement:

“A square is a polygon made up of four line segments, out of which, the length of three line segments are equal to the length of the fourth one and all its angles are right angles”.

Define the terms used in this definition which you feel necessary. Are there any undefined terms in this? Can you justify that all angles and sides of a square are equal?

Ans: The terms used in this definition which needs to be defined are:

Polygon: A polygon is a two dimensional simple closed figure, made up of three or more line segments.

Line segments: A line segment is a part of a line with finite length, having two endpoints.

Angle: An angle is the formation obtained after two rays are initiated from a common point.

Right Angle: The measure of an angle is 90° then it is known as a right angle.

Ray: Ray is a part of a line with only one endpoint and moves endlessly in the other direction.

The undefined terms used here are a line and a point.

Here, we are given that all the angles of a square are right angles.

Now, according to Euclid’s fourth postulate which illustrates that,“all right angles are equal to one another,” we can say that all the angles of a square are equal to one another.

Also, we are given that the length of three line segments are equal to the length of the fourth one.

Now, according to Euclid’s first axiom which illustrates that,“things which are equal to the same thing are equal to one another,” we can say that all sides of a square are equal to one another.

Exercise 5.4

1. Read the following statement:

An equilateral triangle is a polygon made up of three line segments out of which two line segments are equal to the third one and all its angles are 60° each.

Define the terms used in this definition which you feel necessary. Are there any undefined terms in this? Can you justify that all sides and all angles are equal in an equilateral triangle?

Ans: There are some of the terms used in the above definition which can be defined separately. They are:

Triangle: A triangle is a three sided closed figure made up of line segments. It is a three sided polygon.

Polygon: A polygon is a closed figure made up of at least three or more line segments. Ex-  a square, hexagon.

Line segment: A line segment is a finite part of a line with two endpoints having a finite length.

Angle: When two rays initiate from a common initial point they create an angle.

Ray: A line with one fixed end and extended indefinitely in the other direction.

Acute angle: An angle whose measure is between 0° and 90°.

The undefined terms used here are a line and a point.

The justification for an equilateral triangle can be given as:

In a triangle, if two line segments are equal to the third line segment then all the three sides of an equilateral triangle are equal.

Also, all of its angles are 60° each. Therefore, all three angles of an equilateral triangle are equal.

This is illustrated by Euclid's first axiom, which states that “things which are equal to the same things are equal to one another.”

Therefore, all the sides and angles are equal in an equilateral triangle. 

2. Study the following statement:

“Two intersecting lines cannot be perpendicular to the same line”. Check whether it is an equivalent version to the Euclid’s fifth postulate. \[\text{[Hint: Identify the two intersecting lines l and m and the line n in the above statement.]}\]

Ans: Two intersecting lines, say l and m, cannot be perpendicular to the same third line because if two lines l and m are perpendicular to another line n, then the lines l and m must be parallel. Which is not possible because the lines l and m are intersecting lines which cannot be parallel.

Hence, the given statement is not an equivalent version of Euclid’s fifth postulate.

3. Read the following statements which are taken as axioms:

(i) If a transversal intersects two parallel lines, then corresponding angles are not necessarily equal.

(ii) If a transversal intersects two parallel lines, then alternate interior angles are equal.

Is this system of axioms consistent? Justify your answer.

Ans: No. The given system of axioms is not consistent because if a transversal line intersects two parallel lines and then if the corresponding angles are not found to be equal, then the alternate interior angles also cannot be equal. In that case, the lines will not be considered to be parallel.

However, if a transversal line intersects a set of two parallel lines then the corresponding angles as well as the alternate interior angles formed, are always equal.

4. Read the following two statements which are taken as axioms:

(i) If two lines intersect each other, then the vertically opposite angles are not equal.

(ii) If a ray stands on a line, then the sum of two adjacent angles so formed is equal to 180°.

Is this system of axioms consistent? Justify your answer.

Ans: No. The given system of axioms is not consistent because if a ray is standing on a line and then the sum of the two formed adjacent angles is equal to 180°, then if any two lines which intersect each other will have their vertically opposite angle equal to each other.

5. Read the following axioms:

(i) Things which are equal to the same thing are equal to one another.

(ii) If equals are added to equals, the wholes are equal.

(iii) Things which are double of the same thing are equal to one another.

Check whether the given system of axioms is consistent or inconsistent.

Ans: The given system of axioms are Euclid’s first, second and third axioms, therefore they are consistent.

Euclid's Mathematical Theories that have been Mentioned are:

• Brief accentuation has been put toward the start of the chapter to portray the origin and significance of geometry. 

• Without Geometry, the development of dams, structures, extensions would have been unimaginable. 

• It is with the solid establishment laid by the famous mathematicians that the hypotheses are developing.

• The components of geometry have been segregated and referenced in the book of Euclid. 

• Euclid's geometry further clarified the wordings: Spheres, surfaces, curves, dimensions and focuses. 

• The separation and relativity among Axioms and Postulates have been advised.