NCERT Exemplar for Class 11 Physics Chapter 7 - Systems of Particles and Rotational Motion (Book Solutions)

MCQ I

7.1 For which of the following does the center of mass lie outside the body?

(a) A pencil

(b) A shotput

(c) A dice

(d) A bangle

Ans: Option (d) is correct because a bangle is a ring like form with the centre of mass of the ring located outside the ring or bangle. 

7.2 Which of the following points is the likely position of the centre of mass of the system shown in Fig. 7.1?

(a) ${\text{A}}$

(b) ${\text{B}}$

(c) ${\text{C}}$

(d) D

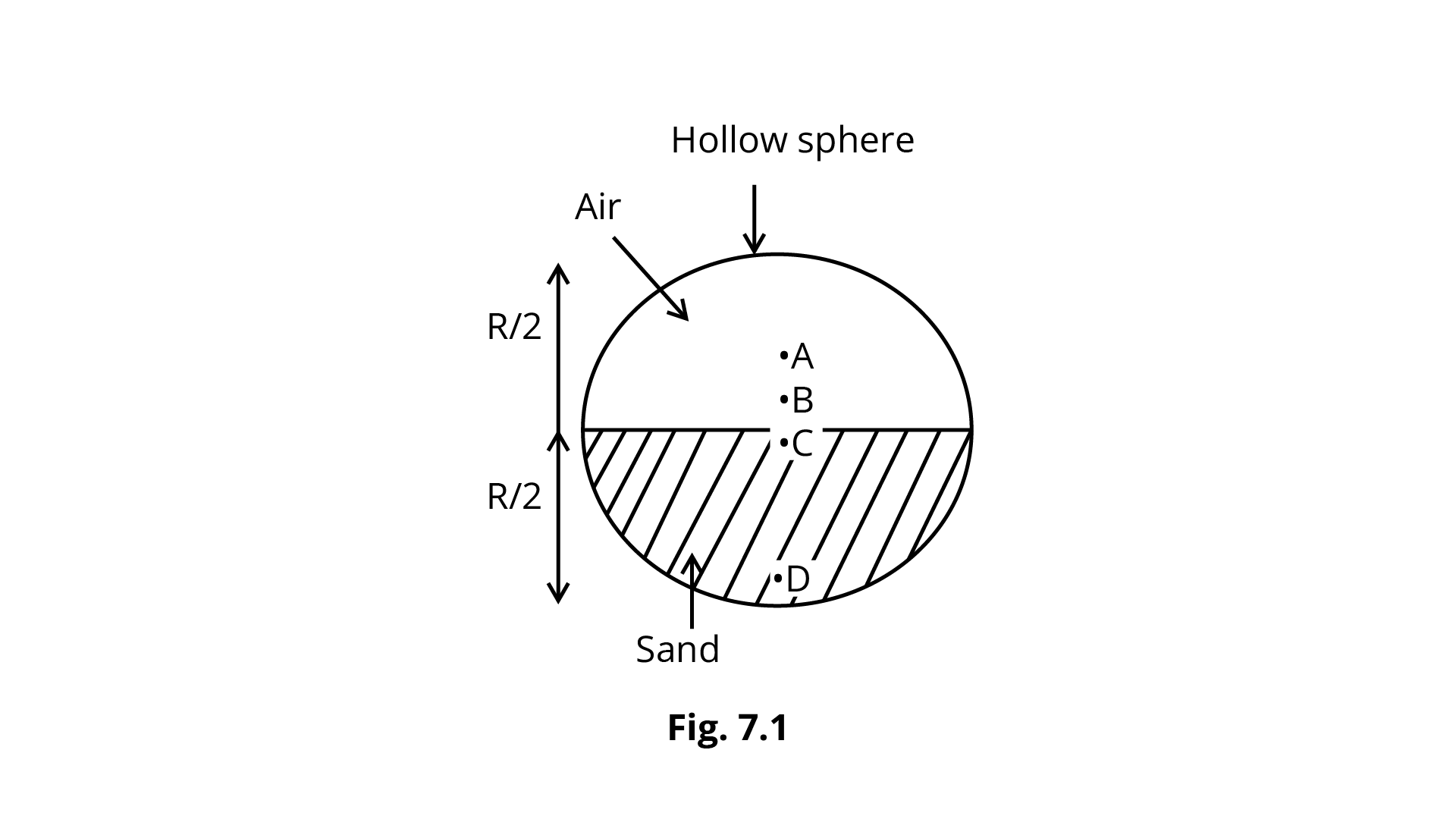
Ans: Option (c) is correct because the volume of air and sand is half that of a sphere, the volume of sand is equal to the volume of air. The pressure in the air zone is smaller than the pressure in the sand region, i.e.

${P_{air}} <  < {P_{sand}}$

$\therefore {M_{sand}} >  > {M_{air}}$ 

Because the mass of sand is more than the mass of air, the centre of mass will migrate towards sand from the centre of sphere B, i.e., the system's centre mass is at C.

7.3 A particle of mass m is moving in y-zplane with a uniform velocity v with its trajectory running parallel to \[ + \]ve y-axis and intersecting z-axis at \[{\mathbf{z}} = {\mathbf{a}}\](Fig. 7.2). The change in its angular momentum about the origin as it bounces elastically from a wall at y\[ = \] constant is:

(a) $m v a \hat{e}_{x}$

(b) $2 \mathrm{mv} a \hat{e}_{x}$

(c) $V \mathrm{mv} \hat{e}_{x}$

(d) $2 y \mathrm{mv} \hat{\mathrm{e}}_{x}$

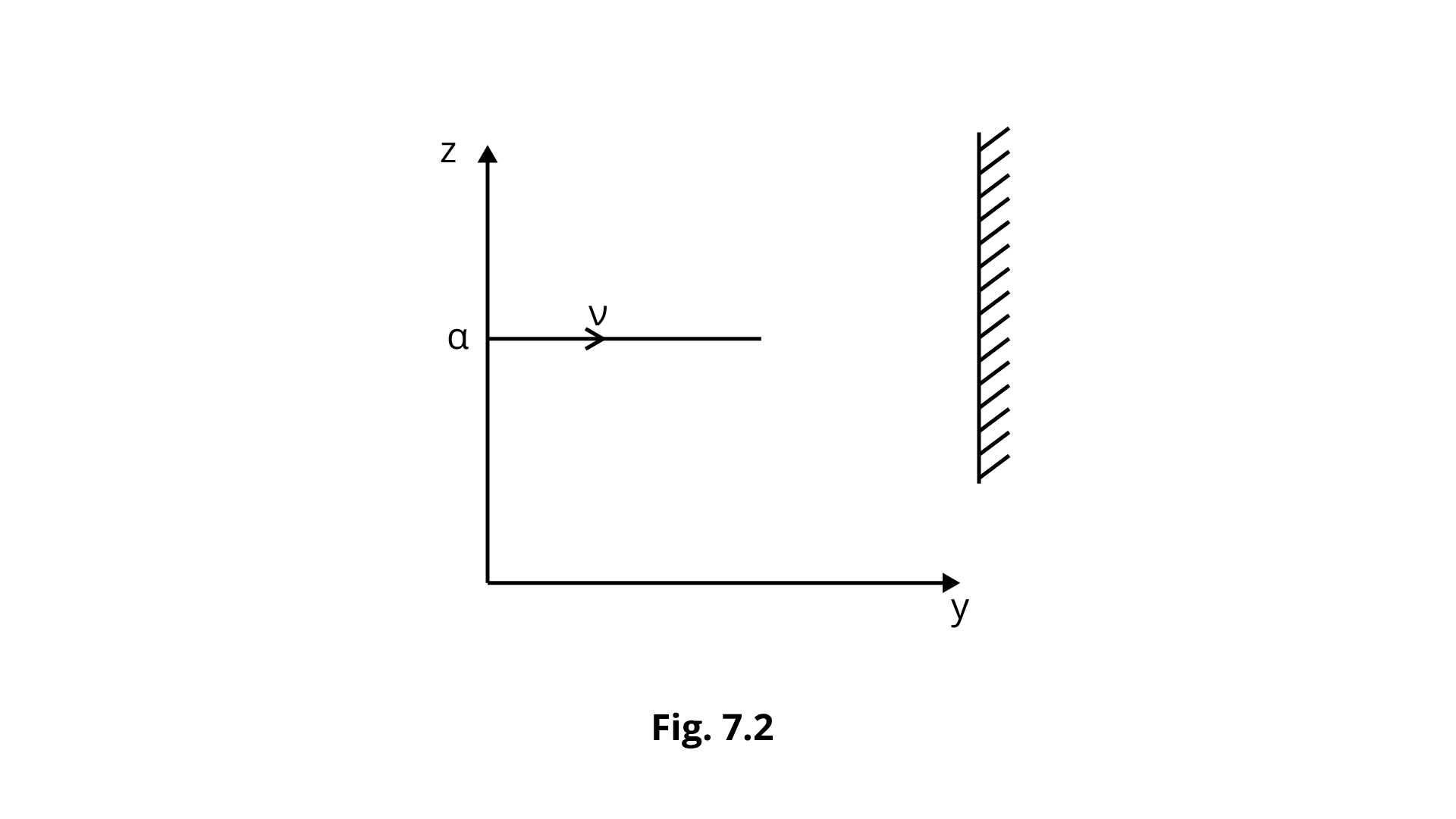
Ans: Option (b) is correct because position particle moving in the direction of $y - axis$ is

$\vec{r}=y \hat{e}_{y}+a \hat{e}_{z}$

${v_i} = v{{\hat e}_y}\quad $

${v_f} =  - v{{\hat e}_y}$

$\vec L = \vec r \times \vec p$ 

\[{\text{y - z}}\] plane has $\vec r,\vec v$and $\vec p$.

Now, 

$L = \left( {y{{\hat e}_y} + a{{\hat e}_z}} \right) \times m\left( {{v_f} - {v_1}} \right)$

$L = \left( {y{{\hat e}_y} + a{{\hat e}_z}} \right) \times m\left[ { - v{{\hat e}_y} - v{{\hat e}_y}} \right]$

$L = \left( {y{{\hat e}_y} + a{{\hat e}_z}} \right) \times mv\left( { - 2{{\hat e}_y}} \right)$

$\because y\hat e \times {{\hat e}_y} = y\sin {0^\circ } = 0$

$a{{\hat e}_z} \times {{\hat e}_y} = a\sin {90^\circ }\left( { - {{\hat e}_x}} \right) =  - a{{\hat e}_x}$

$\therefore L =  - a{{\hat e}_x}mv( - 2) =  + 2amv{{\hat e}_x}$ 

7.4 When a disc rotates with uniform angular velocity, which of the following is not true?

(a) The sense of rotation remains same.

(b) The orientation of the axis of rotation remains same.

(c) The speed of rotation is non-zero and remains same.

(d) The angular acceleration is non-zero and remains same.

Ans: Option (d) is correct because $\omega $ remains same. So, 

$\therefore \alpha  = \dfrac{{d\omega }}{{dt}} \Rightarrow \alpha  = 0$

7.5 A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind (Fig. 7.3). The moment of inertia about the z-axis is then

(a) increased

(b) decreased

(c) the same

(d) changed in unpredicted manner.

Ans: Option B is correct because after the matter is removed from Q, it is stuck at P through the axis of rotation, but the axis of rotation does not pass through Q. As a result, it becomes closer to the axis of rotation.

7.6 In problem 7.5, the CM of the plate is now in the following quadrant of x-y plane,

(a) I

(b) II

(c) III

(d) IV

Ans: Option (c) is correct because the mass at Q is reduced and moved to the centre of mass, the new C.M. will shift to the opposite side of Q on the line connecting QP. 

As a result, the new C.M. is situated in III quadrant.

7.7 The density of a non-uniform rod of length $1\;{\text{m}}$ is given by $\rho (x) = a\left( {1 + b{x^2}} \right)$

where ${\text{a}}$ and ${\text{b}}$ are constants and$o \leqslant x \leqslant 1$.

The centre of mass of the rod will be at

(a) $\dfrac{{3(2 + b)}}{{4(3 + b)}}$

(b) $\dfrac{{4(2 + b)}}{{3(3 + b)}}$

(c) $\dfrac{{3(3 + b)}}{{4(2 + b)}}$

(d) $\dfrac{{4(3 + b)}}{{3(2 + b)}}$

Ans: Option (a) is correct because 

$\rho (x) = a\left( {1 + b{x^2}} \right)$

$p$ is same in this case, which clearly shows that C.M. is $0.5$and C.M. is $0.5$ only at $b = 0$. So, putting value of b in (a) Option, we obtain,

$\dfrac{3}{4} \times \dfrac{2}{3} = \dfrac{1}{2} = 0.5m$

7.8 A Merry-go-round, made of a ring-like platform of radius R and mass M, is revolving with angular speed$\omega $. A person of mass M is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as seen from the round). The speed of the round afterwards is

(a) $2\omega $

(b) $\omega $

(c) $\dfrac{\omega }{2}$

(d) \[{\mathbf{0}}\]

Ans: Option (a) is correct because 

${I_1}{\omega _1} = {I_2}{\omega _2}$

${m_1} = 2M\quad $

${m_2} = M\quad $

${\omega _1} = \omega \quad $

${\omega _2} = ?$

${r_1} = R\quad $

${r_2} = R$ 

When a person leaps down tangentially, i.e. from the perimeter,

$\therefore {m_1}r_1^2{\omega _1} = {m_2}r_2^2{\omega _2}$

$2M{R^2}\omega  = M{R^2}{\omega _2}$

${\omega _2} = 2\omega $ 

MCQ II

7.9 Choose the correct alternatives:

(a) For a general rotational motion, angular momentum ${\mathbf{L}}$ and angular velocity ${\mathbf{\omega }}$ need not be parallel.

(b) For a rotational motion about a fixed axis, angular momentum ${\mathbf{L}}$ and angular velocity${\mathbf{\omega }}$are always parallel.

(c) For a general translational motion, momentum ${\mathbf{p}}$ and velocity vare always parallel.

(d) For a general translational motion, acceleration a and velocity ${\mathbf{v}}$ are always parallel.

Ans: Option (a) and (c) are correct because For general rotational motion with an asymmetric axis of rotation. 

Angular momentum and angular velocities are not the same thing. It proved that Option (a) is absolutely correct.

Momentum in general translation motion

$\vec p = m\vec v$

$\vec p$and $\vec v$ are in the same direction at all times. It proved that Option (c) is absolutely correct.

7.10 Figure 7.4 shows two identical particles $1$ and $2$ , each of mass m, moving in opposite directions with same speed ${\mathbf{v}}$ along parallel lines. At a particular instant, ${{\mathbf{r}}_1}$and ${{\mathbf{r}}_2}$ are their respective position vectors drawn from point A which is in the plane of the parallel lines. Choose the correct options:

(a) Angular momentum ${{\mathbf{l}}_1}$ of particle $1$ about ${\text{A}}$ is ${{\mathbf{l}}_1} = {\operatorname{mud} _1}$.

(b) Angular momentum ${{\mathbf{l}}_2}$ of particle $2$ about ${\text{A}}$ is ${{\mathbf{l}}_2} = {\operatorname{mv} _2}$.

(c) Total angular momentum of the system about ${\text{A}}$ is ${\mathbf{l}} = mv\left( {{{\mathbf{r}}_1} + {{\mathbf{r}}_2}} \right)$.

(d) Total angular momentum of the system about ${\text{A}}$ is ${\mathbf{l}} = mv\left( {{d_2} - {d_1}} \right)$

$ \otimes $represents a unit vector coming out of the page.

$ \otimes $represents a unit vector going into the page.

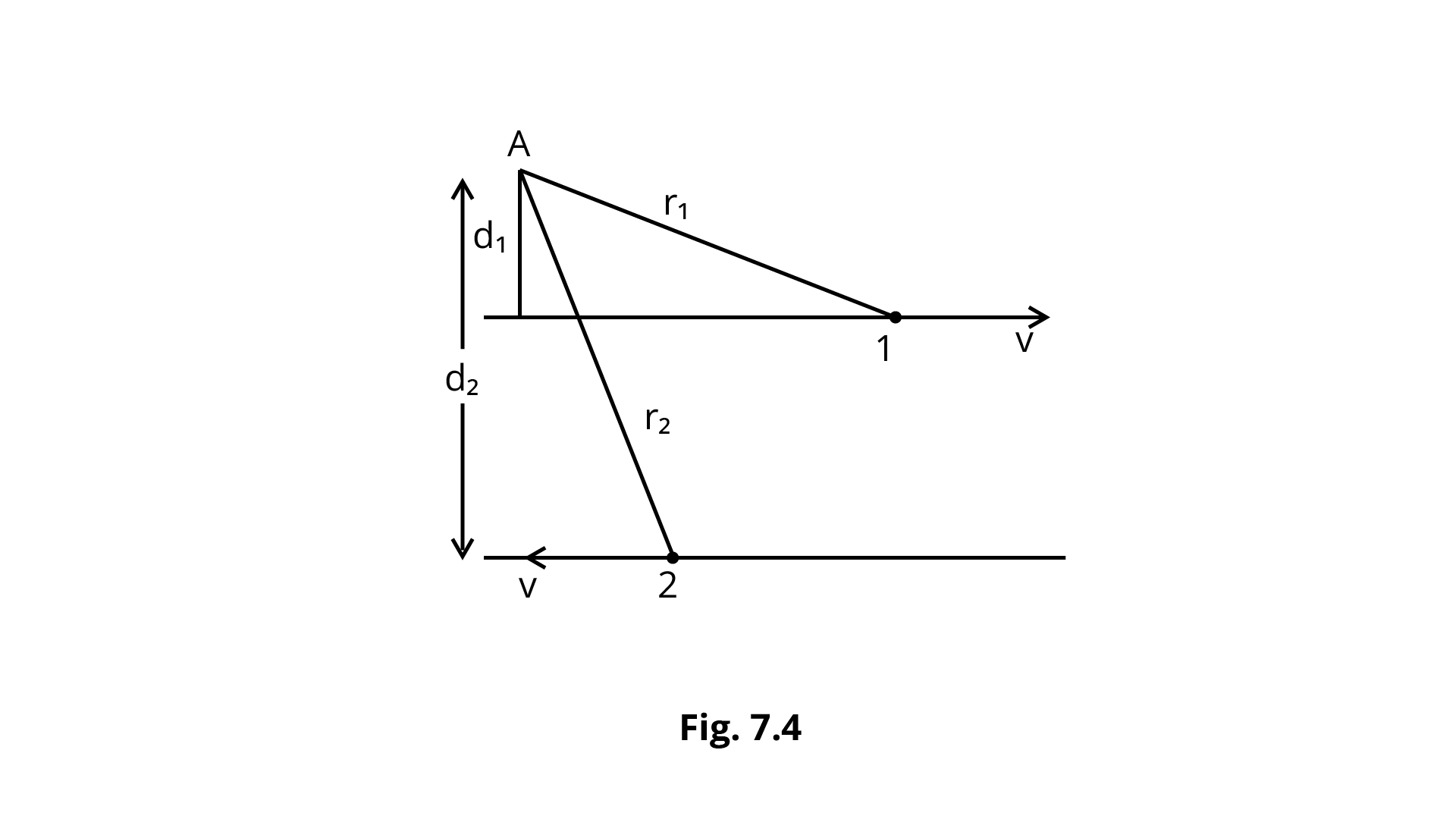
Ans: Option (a) and (d) are correct because 

Particle 1,

${\bar L_{ - 1}} = {\bar r_1} \times \bar p \odot $

${{\bar L}_1} = {{\bar r}_1} \times m\bar v \odot  = m\bar v{d_1} \odot $

${{\vec L}_2} = {{\vec r}_1} \times m( - \bar v) \otimes  =  - m\bar v{d_2} \otimes $ 

It means that Option (a) is absolutely correct.

Whole Angular Momentum, $\bar L -  = {\bar L_1} + {\bar L_2}$

$\bar L -  = m\bar v{d_1} \odot  - m\bar v{d_2} \otimes $

${d_2} > {d_1}\quad \therefore \left| {{{\vec L}_2}} \right| > \left| {{{\vec L}_1}} \right|$ 

$\therefore \quad \vec L = m\vec v\left( { - {d_2} - {d_1}} \right) \otimes $

It means that Option (d) is absolutely correct.

7.11 The net external torque on a system of particles about an axis is zero. Which of the following are compatible with it ?

(a) The forces may be acting radially from a point on the axis.

Ans: This is compatible with the situation given in the question because

$\tau  = \vec r \times \vec F$

$\vec t -  = \vec r \times \vec F -  = rF\sin \theta \hat n$

Because the forces are radially directed $\bar r$,

$\therefore \quad \tau  = rF\sin {0^\circ } = 0$

It means that Option (a) is absolutely correct.

(b) The forces may be acting on the axis of rotation.

Ans: This is compatible with the situation given in the question because if there are forces operating on the axis of rotation, then$\theta  = {0^\circ }$

So, $\tau  = 0$

It means that Option (b) is absolutely correct.

(c) The forces may be acting parallel to the axis of rotation.

Ans: This is compatible with the situation given in the question because When forces (F) are parallel to the axis of rotation, their component in the plane of $\vec r$ and $\vec F$${\text{ = F}}\cos {90^\circ } = 0.$

As a result, ${\text{F}} = 0 \Rightarrow \tau  = 0$ 

It means that Option (c) is absolutely correct.

(d) The torque caused by some forces may be equal and opposite to that caused by other forces.

Ans: This is compatible with the situation given in the question because when torques are equal and opposing, net torque$ = {\tau _1} - {\tau _2} = 0$. It means that Option (d) is absolutely correct.

7.12 Figure 7.5 shows a lamina in x-y plane. Two axes z and ${z^\prime }$ pass perpendicular to its plane. A force F acts in the plane of lamina at point P as shown. Which of the following are true? (The point P is closer to${z^\prime }$-axis than the z-axis.)

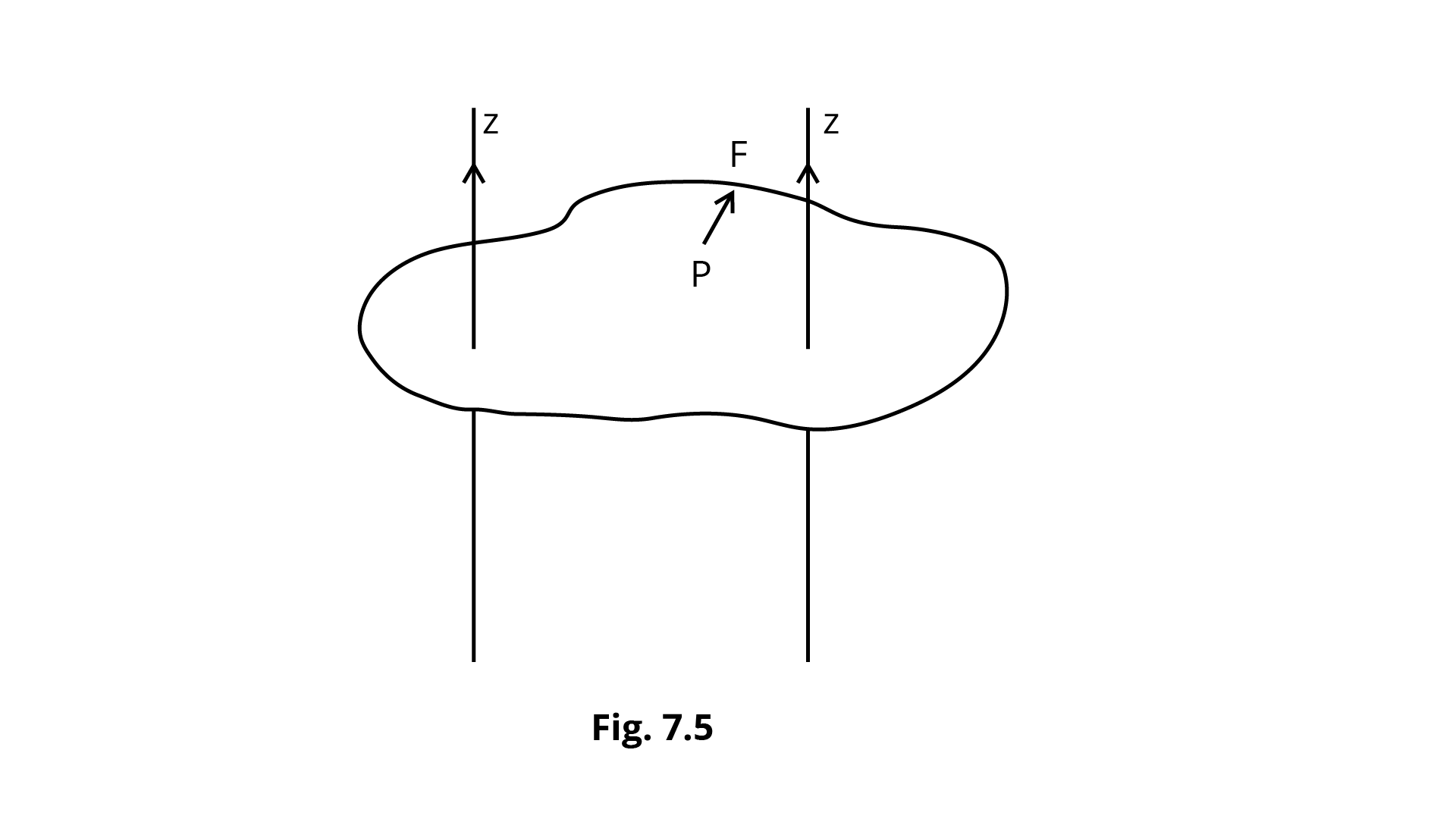
(a) Torque $\tau $ caused by F about z- axis is along$ - \widehat {\mathbf{k}}$.

Ans: This is true because ${r^\prime } < r$

${{\bar \tau }_z} = {{\bar r}^\prime } \times \bar F$

${\tau _z} = rF\sin {\theta ^\prime }( + \hat k).$ 

$\bar r$and $\vec F$are $x - y$ plane.

Applying Right Hand Grip Thumb Rule,

$\vec r \times \vec F$is $ + \hat k$ direction.

(b) Torque ${\tau ^\prime }$ caused by F about ${z^\prime }$ axis is along$ - \widehat {\mathbf{k}}$.

Ans: This is true because $\vec \tau  = \vec r \times \vec F = rF\sin \theta ( - \hat K)$. This rationale is quite similar with the (a) Option reason.

(c) Torque $\tau $ caused by F  about ${\mathbf{z}}$ axis is greater in magnitude than that about z axis.

Ans: This is true because 

$\because r > {\tau ^\prime }$

$\theta  > {\theta ^\prime }$

$\sin \theta  > \sin {\theta ^\prime }$

$rF\sin \theta  > {r^\prime }F\sin {\theta ^\prime }$

${\tau _z} > {\tau _z}$ 

(d) Total torque is given be$\tau  = {\tau _z} + {\tau _{{z^\prime }}}$.

Ans: This is False because 

$\tau  = {\tau _z} + {\tau _{{z^\prime }}}$if ${\tau _z}$and ${\tau _{{z^\prime }}}$will be in same axis. But its not possible at all. 

7.13 With reference to Fig. 7.6 of a cube of edge a and mass m, state whether the following are true or false. (${\text{O}}$is the centre of the cube.)

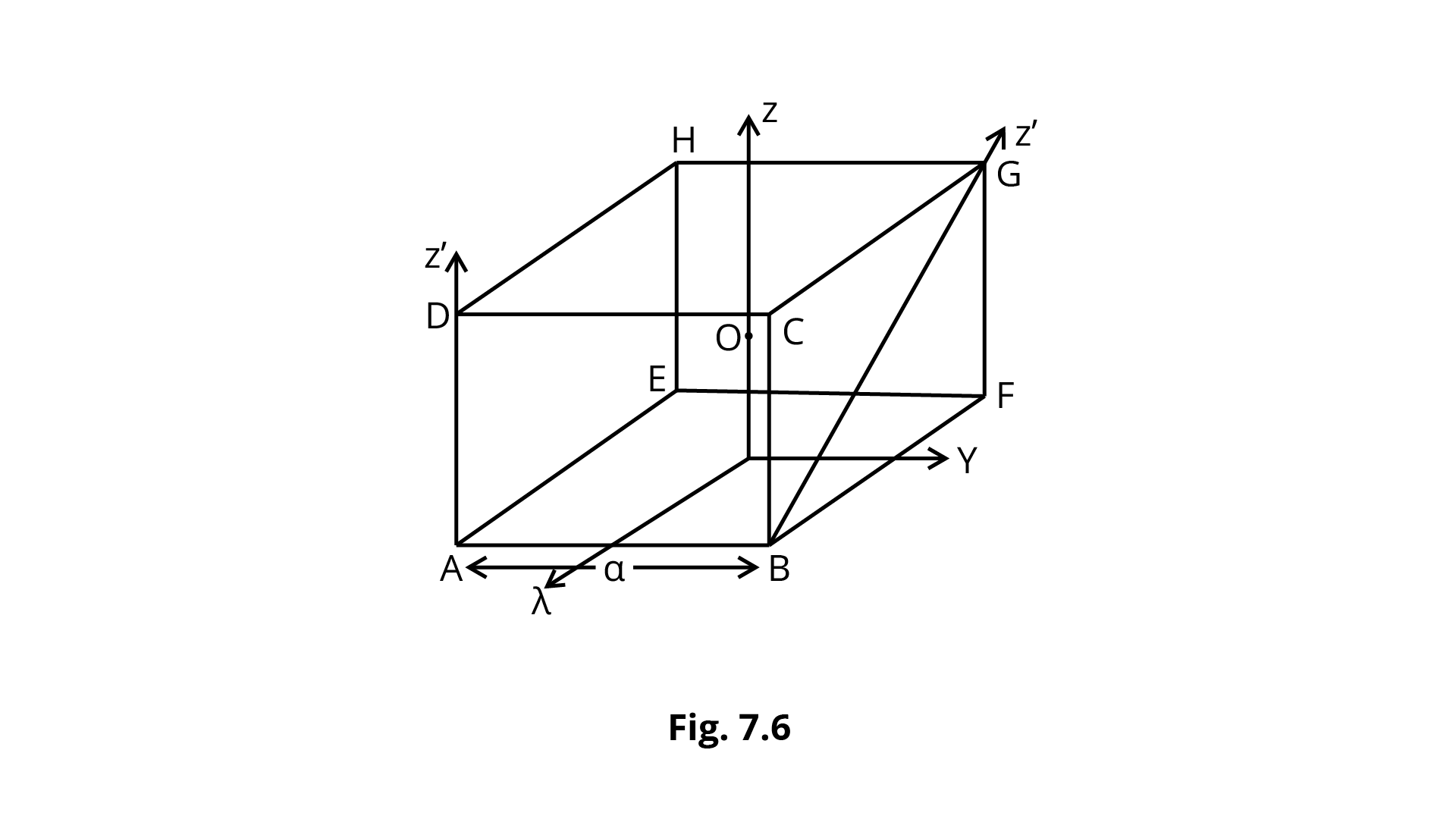
(a) The moment of inertia of cube about z-axis is ${I_z} = {I_x} + {I_y}$

Ans: This is True because z-axis is perpendicular to both x-y axis,

By applying perpendicular theorem,

\[{{\text{I}}_{\text{z}}}{\text{ = }}{{\text{I}}_{\text{x}}}{\text{ + }}{{\text{I}}_{\text{y}}}\]

(b) The moment of inertia of cube about ${z^\prime }$ is $I_z^\prime  = {I_z} + \dfrac{{m{a^2}}}{2}$

Ans: This is True because according to the parallel axis theorem, z and z'-axis are parallel, and the distance between z and z'-axis is equal to 

$\dfrac{d}{2} = \dfrac{{DG}}{2} = \dfrac{1}{2}\sqrt {{a^2} + {a^2}}  = \dfrac{{\sqrt {2{a^2}} }}{2}$

${I_{z = }} = {I_z} + M{\left( {\dfrac{a}{{\sqrt 2 }}} \right)^2} = {I_z} + \dfrac{{m{a^2}}}{2}$

(c) The moment of inertia of cube about ${z^{\prime \prime }}$ is $ = {I_z} + \dfrac{{m{a^2}}}{2}$

Ans: This is False because Because axis BG, i.e., z" and z-axis, are not parallel,

the parallel axis theorem cannot be used.

(d) ${I_x} = {I_y}$

Ans: This is True because the z-axis goes through the centre O of the cube, the and y-axes are symmetric.

\[{{\text{I}}_{\text{x}}}{\text{ = }}{{\text{I}}_{\text{y}}}\]

VSA

7.14 The centre of gravity of a body on the earth coincides with its centre of mass for a 'small' object whereas for an 'extended' object it may not. What is the qualitative meaning of 'small' and 'extended' in this regard? For which of the following the two coincides? A building, a pond, a lake, a mountain?

Ans: While the centre of gravity is the centre of its geometry, the centre of mass is the point at which the entire mass of the body may be regarded. 

When an item's vertical height or geometric centre is extremely close to the earth's surface, the thing is said to be tiny. When it is larger, it is referred to as an expanded object.

Because a building (high) and a pond are little things, while a mountain and a lake are large objects, their geometrical centres will lie above and below the earth's surface, respectively, with substantial distances, resulting in what are known as stretched objects.

7.15 Why does a solid sphere have smaller moment of inertia than a hollow cylinder of same mass and radius, about an axis passing through their axes of symmetry?

Ans: 

$I = \sum\limits_{i = 1}^n {{m_i}} r_i^2$

The moment of inertia is related to the square of the mass's distance from the axis of rotation. The whole mass of a solid sphere is spread from the centre to the radius of the sphere R. However, because the whole mass of a hollow sphere is concentrated towards the sphere's periphery or surface, the average value of \[{r_{i\;}}\] in a hollow sphere is greater than in a solid sphere. As a result, the MI of a hollow sphere is greater than that of a solid spherical.

7.16 The variation of angular position$\theta $, of a point on a rotating rigid body, with time t is shown in Fig. 7.7. Is the body rotating clock-wise or anti-clockwise?

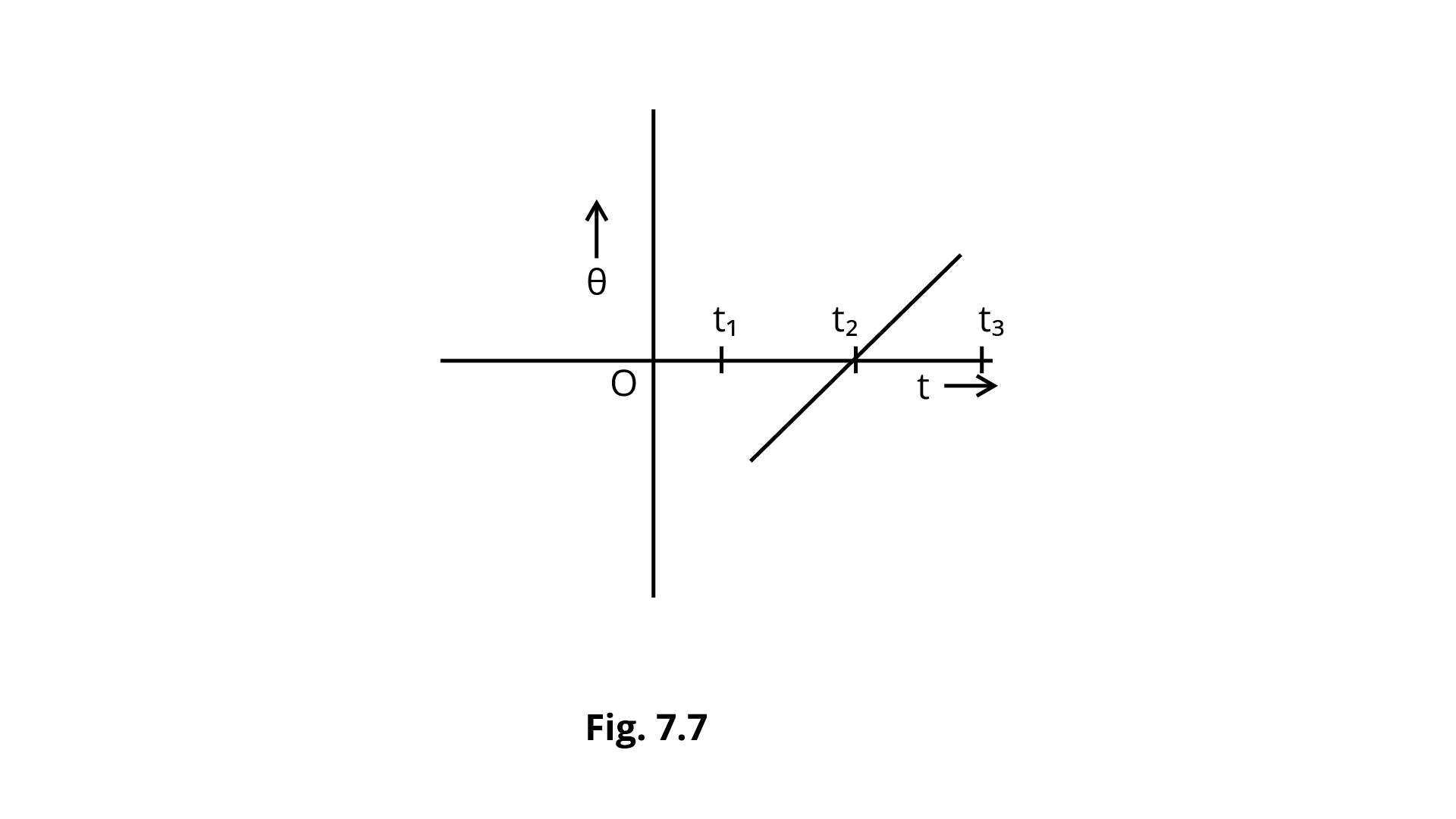
Ans: Graph $\theta  - t$is having positive slope. As a result, $\dfrac{{d\theta }}{{dt}} = \omega $ is also positive. So the body rotating clock-wise.

7.17 A uniform cube of mass m and side a is placed on a frictionless horizontal surface. A vertical force ${\mathbf{F}}$ is applied to the edge as shown in Fig. 7.8. Match the following (most appropriate choice):

Ans: 

7.18 A uniform sphere of mass m and radius R is placed on a rough horizontal surface (Fig. 7.9). The sphere is struck horizontally at a height h from the floor. Match the following:

Ans: 

SA

7.19 The vector sum of a system of non-collinear forces acting on a rigid body is given to be non-zero. If the vector sum of all the torques due to the system of forces about a certain point is found to be zero, does this mean that it is necessarily zero about any arbitrary point?

Ans: At a given place, the vector sum of all torques owing to forces equals zero. 

This does not imply that the sum of the forces is zero. 

For example, a boy's and a child's torque on a sea-saw might be the same (can be balance). 

The torques will not blanch the sea-saw if the point of support moves without changing its position. 

As a result, if the total of all torques owing to distinct forces at a location is zero, it is not required that it will be zero for any other random point.

${G_i}\sum\limits_{i = 1}^n {{F_i}}  \ne 0$

Let, 

$\tau  = {\tau _1} + {\tau _2} +  \ldots  + {\tau _n} = \sum\limits_{i = 1}^n {{{\vec r}_i}}  \times {\vec F_i} = 0$

At other point $\tau $, varied forces is ${\vec r_i}$

$\sum\limits_{i = 1}^n {\left( {{{\vec r}_i} - a} \right)}  \times {F_i} = \sum\limits_{i = 1}^n {\vec r}  \times {F_i} - a\sum\limits_{i = 1}^n {{F_1}} $

$\sum {{F_i}}  \ne 0$

As a result, the total of all torques about any arbitrary point does not have to be zero.

7.20 A wheel in uniform motion about an axis passing through its centre and perpendicular to its plane is considered to be in mechanical (translational plus rotational) equilibrium because no net external force or torque is required to sustain its motion. However, the particles that constitute the wheel do experience a centripetal acceleration directed towards the centre. How do you reconcile this fact with the wheel being in equilibrium?

How would you set a half-wheel into uniform motion about an axis passing through the centre of mass of the wheel and perpendicular to its plane? Will you require external forces to sustain the motion?

Ans: A stiff rigid elastic body is a wheel. 

It moves uniformly along an axis that runs through its centre and is perpendicular to the plane of the wheel. 

Each wheel particle is in circular motion about the above axis, and each particle will experience a centripetal acceleration directed towards the axis of rotation due to elastic forces that act in pairs. The distribution of mass in a half wheel is not symmetric about the wheel's axis. 

As a result, the directions of angular momentum and angular velocity do not coincide. 

As a result, external torque is necessary to sustain motion in the half wheel.

7.21 A door is hinged at one end and is free to rotate about a vertical axis (Fig. 7.10). Does its weight cause any torque about this axis? Give reason for your answer.

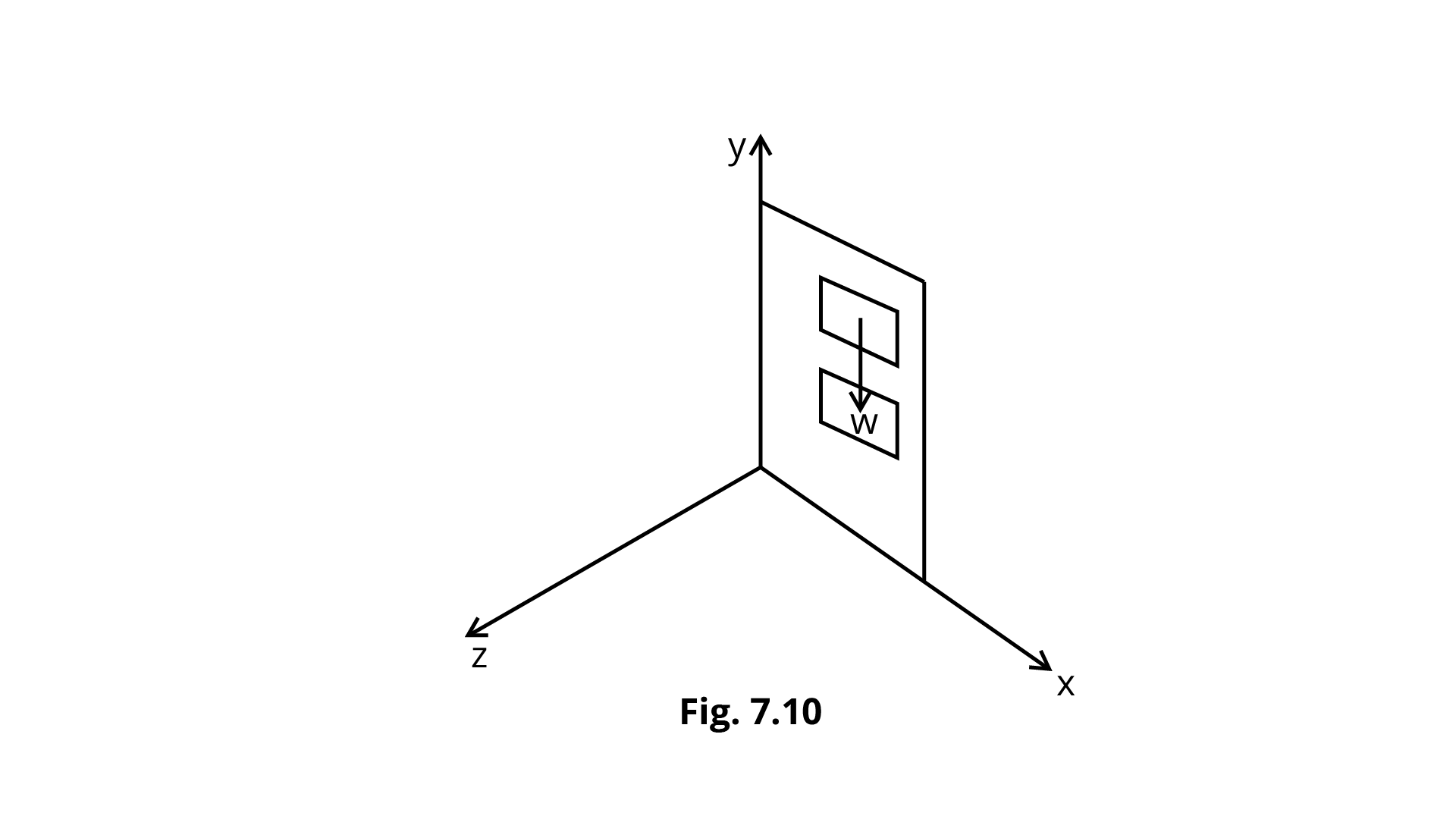
Ans: $\vec \tau  -  = \vec r \times \vec F$

The torque is experienced by the door when the axis of rotation of the door is along the Y-axis and the door is in the X-y plane, and force F may be applied along the $ \pm z - $axis. 

As a result, a force can only create torque along an axis in the direction normal to the force. 

The force of gravity on the door is parallel to the axis of rotation. 

As a result, torque cannot be produced along the y-axis. 

Gravity is along the -y axis as a result of the door. 

As a result, it may spin the door in axis along the $ \pm z - $axis.

As a result, the weight of the door cannot rotate it along the y-axis.

7.22 $(n - 1)$ equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector a with respect to the centre of the polygon. Find the position vector of centre of mass.

Ans: A regular n-center polygon's of mass is located in its geometric centre. 

Let $\vec b$ be the position vector of a regular n-center polygon's of mass. 

When $(n - 1)$ equal point masses are placed at the vertices of an n-polygon,${r_{cm}}$ is computed when mass m is placed at the \[{n^{th}}\] vertex.

${r_{cm}} = \dfrac{{(n - 1)mb + ma}}{{(n - 1)m + m}}$

${r_{cm}} = 0$

$\dfrac{{(n - 1)mb + ma}}{{(n - 1)m + m}} = 0$

$(n - 1)mb + ma = 0$

$b =  - \dfrac{{ma}}{{(n - 1)m}}$

$\Rightarrow \vec b =  - \dfrac{{\vec a}}{{(n - 1)}}$ 

(-)sign indicates that c.m. is on opposite side of the nth vertex geometrical centre of 

the n-polygon, i.e., $\vec b$is the inverse of the vector $\vec a$- (form centre to \[{n^{th}}\] vertex).

LA

7.23 Find the centre of mass of a uniform 

(a) half-disc

Ans: Let M be the mass of one-half of a disc.

Half disc’s area$ = \dfrac{{\pi {R^2}}}{2}$

Mass/Area $ = \dfrac{{2M}}{{\pi {R^2}}}$

The half disc can be split into several semicircular strips.

Radi vary from $0 \to R$

Semicircular strip’s surface area $ = \dfrac{\pi }{2}\left[ {{{(r + dr)}^2} - {r^2}} \right]$

$= \dfrac{\pi }{2}\left[ {{r^2} + d{r^2} + 2rdr - {r^2}} \right]$

$= \pi rdr$ 

$\therefore dm = \dfrac{{2M}}{{\pi {R^2}}} \cdot \pi rdr$

${\text{dm}} = \dfrac{{2M}}{{{R^2}}} \cdot rdr$ 

Assume that $(x,y)$ are co-ordinates of strip,

$(x,y) = \left( {0,\dfrac{{2r}}{\pi }} \right)$

$x = {x_{cm}} = \dfrac{1}{M}\int_0^R x dm = \int_0^R 0 dm = 0$

${y_{cm}} = \dfrac{1}{M}\int_0^R y dm = \dfrac{1}{M}\int_0^R {\dfrac{{2r}}{\pi }}  \times \dfrac{{2M}}{{{R^2}}}rdr$

$= \dfrac{1}{m} \cdot \dfrac{{4M}}{{\pi {R^2}}}\int_0^R {{r^2}} dr = \dfrac{4}{{\pi {R^2}}}\left[ {\dfrac{{{r^3}}}{3}} \right]_0^R = \dfrac{4}{{3\pi {R^2}}} \cdot {R^3}$

${y_{cm}} = \dfrac{{4R}}{{3\pi }}$ 

Centre of mass is $0$and $4R$.

(b) quarter-disc

Ans:  Quarter disc mass per unit area a uniform quarter disc's centre of mass

$ = \dfrac{M}{{\dfrac{{\pi {R^2}}}{4}}} = \dfrac{{4M}}{{\pi {R^2}}}$

For a half disc along y-axis c.m. at $y = \dfrac{{4R}}{{3\pi }}$

So the c.m. of quarter disc $ = $$\dfrac{{4R}}{{3\pi }}$.

7.24 Two discs of moments of inertia ${I_1}$ and ${I_2}$ about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed ${\omega _1}$ and ${\omega _2}$ are brought into contact face to face with their axes of rotation coincident.

(a) Does the law of conservation of angular momentum apply to the situation? Why?

Ans: As there is no net external torque on system, the law of conservation of angular 

momentum may be applied. 

Gravitational forces and their normal reactions are external forces, but their net torque is zero, therefore they have no impact.

(b) Find the angular speed of the two-disc system.

Ans: By applying Law of conversation of angular momentum,

${L_j} = {L_i} \Rightarrow I\omega  = {I_1}{\omega _1} + {I_2}{\omega _2}$

$I = $moment of Inertia

$\omega  = $angular speed

$\therefore \omega  = \dfrac{{{I_1}{\omega _1} + {I_2}{\omega _2}}}{I}\quad \because I = {I_1} + {I_2}$

$\therefore \omega  = \dfrac{{{I_1}{\omega _1} + {I_2}{\omega _2}}}{{{I_1} + {I_2}}}$ 

(c) Calculate the loss in kinetic energy of the system in the process.

Ans: As \[{{\text{K}}_{\text{j}}}{\text{ = K }}{{\text{E}}_{\text{R}}}{\text{ + K }}{{\text{T}}_{\text{T}}}\]

Translational Energy$ = 0$

$\therefore K{E_T} = 0$

$\therefore {K_f} = K{E_R} = \dfrac{1}{2}I{\omega ^2} = \dfrac{1}{2}\left( {{I_1} + {I_2}} \right){\left[ {\dfrac{{\left( {{I_1}{\omega _1} + {I_2}{\omega _2}} \right)}}{{{I_1} + {I_2}}}} \right]^2}$

${K_f} = \dfrac{1}{2}\dfrac{{{{\left( {{I_1}{\omega _1} + {I_2}{\omega _2}} \right)}^2}}}{{\left( {{I_1} + {I_2}} \right)}}$

${K_i} = K{E_{1R}} + K{E_{2R}} + K{E_{1T}} + K{E_{2T}}$ 

Because there is no Translational Motion which in turn results,

$K{E_{1T}} = 0$

$K{E_{2T}} = 0$

$\therefore {K_i} = \dfrac{1}{2}{I_1}\omega _1^2 + \dfrac{1}{2}{I_2}\omega _2^2 = \dfrac{1}{2}\left( {{I_1}\omega _1^2 + {I_2}\omega _2^2} \right)$

$\therefore \Delta K = {K_f} - {K_i}$

$= \dfrac{1}{2}\dfrac{{{{\left( {{I_1}{\omega _1} + {I_2}{\omega _2}} \right)}^2}}}{{{I_1} + {I_2}}} - \dfrac{1}{2}\left( {{I_1}\omega _1^2 + {I_2}\omega _2^2} \right)$

$= \dfrac{1}{2}\left[ {\dfrac{{\left. {I_1^2\omega _1^2 + I_2^2\omega _2^2 + 2{I_1}{I_2}{\omega _1}{\omega _2} - \left[ {\left( {{I_1} + {I_2}} \right)\left( {{I_1}\omega _1^2 + {I_2}\omega _2^2} \right)} \right]} \right]}}{{\left( {{I_1} + {I_2}} \right)}}} \right]$ 

$\left[ {I_1^2\omega _2^1 + I_2^2\omega _2^2 + 2{I_1}{I_2}{\omega _1}{\omega _2}} \right] - \left[ {I_1^2\omega _1^2 + I_2^2\omega _2^2 + {I_1}{I_2}\omega _1^2 + I_2^2\omega _2^2} \right]$

$= \left. {\dfrac{{2\left( {{I_1} + {I_2}} \right)}}{{ - \omega _1^2\omega _1^2 + I_2^2 + 2{I_1}{I_2}{\omega _1}{\omega _2} - I_1^2\omega _1^2 - {I_1}{I_2}\omega _2^2}}} \right]$

$= \dfrac{{ - {I_1}{I_2}}}{{2\left( {{I_1} + {I_2}} \right)}}\left( { - 2{\omega _1}{\omega _2} + \omega _2^2 + \omega _1^2} \right)$ 

$\Delta K = \dfrac{{ - {I_1}{I_2}}}{{2\left( {{I_1} + {I_2}} \right)}}{\left( {{\omega _1} - {\omega _2}} \right)^2} < 0$

(d) Account for this loss.

Ans: \[{{\text{K}}_{\text{f}}}{\text{ < }}{{\text{K}}_{\text{i}}}\] since energy is wasted due to friction between discs' moving surfaces.

7.25 A disc of radius R is rotating with an angular speed ${\omega _o}$ about a horizontal axis. It is placed on a horizontal table. The coefficient of kinetic friction is ${\mu _{{k^{}}}}$.

(a) What was the velocity of its centre of mass before being brought in contact with the table?

Ans: Before coming into contact with the table, 

the disc was merely rotating about its axis, 

which passed through the centre. ${\nu _{cm}} = 0$as the point on the axis is regarded to be at rest.

(b) What happens to the linear velocity of a point on its rim when placed in contact with the table?

Ans: When a revolving disc comes into contact with the surface of a table, 

the linear velocity of a point on the rim decreases owing to friction with the table.

(c) What happens to the linear speed of the centre of mass when disc is placed in contact with the table?

Ans: When a rotating disc is placed on the surface of a table, 

Newton's third law produces an action force (change in momentum) on the table in the direction of rotation, and a reaction force is applied to the disc, causing it to move in the direction of the reaction force, so the rotating disc's centre of mass acquires linear velocity. 

As a result of frictional response force.

(d) Which force is responsible for the effects in (b) and (c).

Ans: Force of friction is responsible for the effects in (b) and (c).

(e) What condition should be satisfied for rolling to begin?

Ans: When the disc begins to roll on the table, 

the velocity of the centre of mass ${v_{cm}}$ is caused by the reaction force caused by the rotation angular speed ${\omega _0}$ of the disc of radius R. 

As a result, ${v_{cm}}$ is ${\nu _{cm}} = {\omega _0}$R, when it first comes into touch with the table.

(f) Calculate the time taken for the rolling to begin.

Ans: Acceleration produceed in c.m. ,

$F = ma \Rightarrow a = \dfrac{F}{m} = \dfrac{{{\mu _k}mg}}{m}{\mu _k}g$

$\tau  = I\alpha$

$\Rightarrow \alpha  = \dfrac{\tau }{I} = \dfrac{{r \times F}}{I} = \dfrac{{\vec R \times {\mu _k}mg}}{I} = R{\mu _k}mg\sin \theta$

$\therefore \alpha  = \dfrac{{ - {\mu _k}mgR}}{I}$

${\nu _{cm}} = {u_{cm}} + {a_{cm}}t$(for linear velocity)

${\nu _{cm}} = 0 + {\mu _k}gt = {\mu _k}gt$

$\omega  = {\omega _0} = \alpha t$(for rotational motion)

$\omega  = {\omega _0} - \dfrac{{{\mu _k}mgR}}{I}t$ 

${v_{cm}} = \omega R \Rightarrow \omega  = \dfrac{{{v_{cm}}}}{R}$

$\therefore \dfrac{{{v_{cm}}}}{R} = {\omega _0} - \dfrac{{{\mu _k}mgRt}}{I}$

$\dfrac{{{\mu _k}gt}}{R} = {\omega _0} - \dfrac{{{\mu _k}mgRt}}{I}$

$\dfrac{{{\mu _k}gt}}{R} + \dfrac{{{\mu _k}mgRt}}{I} = {\omega _0}$ 

$\dfrac{{{\mu _k}gt}}{R} + \dfrac{{{\mu _k}mgRt}}{I} = {\omega _0}$

${\mu _k}gt\left[ {\dfrac{1}{R} + \dfrac{{mR}}{I}} \right] = {\omega _0}$

$\dfrac{{{\mu _k}gt}}{R}\left[ {1 + \dfrac{{m{R^2}}}{I}} \right] = {\omega _0}{\text{ or }}$

${\mu _k}gt\left[ {1 + \dfrac{{m{R^2}}}{I}} \right] = {\omega _0}{\text{ or }}\mu $

$_kgt\left[ {1 + \dfrac{{m{R^2}}}{I}} \right] = R{\omega _0}$

$\therefore t = \dfrac{{R{\omega _0}}}{{{\mu _k}g\left[ {1 + \dfrac{{m{R^2}}}{I}} \right]}}$ 

Frictional force aids in pure rolling motion without sliding in this case.

7.26 Two cylindrical hollow drums of radii R and \[{\mathbf{2}}\]R, and of a common height h, are rotating with angular velocities $\omega $(anti-clockwise) and $\omega $(clockwise), respectively. Their axes, fixed are parallel and in a horizontal plane separated by$(3R + \delta )$. They are now brought in contact $(\delta  \to 0)$.

(a) Show the frictional forces just after contact.

Ans: $\because {v_1} = \omega R$

${v_2} = \omega  \cdot 2R = 2\omega R$

At the point of contact C, the directions of ${v_1}$ and ${v_2}$are tangentially upward.

Frictional force (f) operates owing to the difference in velocities of disc 1 and, because f on 1 due to 2 is ${f_{12}} = $upward and ${f_{21}} = $downward, it will be equal and opposite by Newtons Third Law ${f_{12}} =  - {f_{21}}$.

(b) Identify forces and torques external to the system just after contact.

Ans: External Force $ = {f_{12}}$and ${f_{21}}$

$\left| {{f_{12}}} \right| = \left| { - {f_{21}}} \right| = F$

External Torque $ = F \times 3R$ (anti-clockwise)

(c) What would be the ratio of final angular velocities when friction ceases?

Ans: ${v_1} = {v_2}$

${\omega _1}R = 2{\omega _2}R$

$\dfrac{{{\omega _1}}}{{{\omega _2}}} = \dfrac{2}{1}$ 

Ratio $ = 2:1$.

7.27 A uniform square plate S (side c) and a uniform rectangular plate R (sides b, a) have identical areas and masses (Fig. 7.11).

Show that:

(i) \[{{\mathbf{I}}_{{\mathbf{x}}{\mathbf{R}}}}/{{\mathbf{I}}_{{\mathbf{x}}{\mathbf{S}}}} < {\mathbf{1}}\]

Ans: \[{{\text{m}}_{\text{R}}}{\text{ = }}{{\text{m}}_{\text{S}}}{\text{ = m}}\]

${c^2} = ab$

$\because I = m{r^2}$

$\dfrac{{{I_{xR}}}}{{{I_{xs}}}} = \dfrac{{m \cdot {{\left( {\dfrac{b}{2}} \right)}^2}}}{{m{{\left( {\dfrac{c}{2}} \right)}^2}}} = \dfrac{{{b^2}}}{4}\dfrac{4}{{{c^2}}} = \dfrac{{{b^2}}}{{{c^2}}}$ 

$\because c > b$

${c^2} > {b^2}$

$1 > \dfrac{{{b^2}}}{{{c^2}}}\therefore \dfrac{{{I_{xR}}}}{{{I_{xs}}}} < 1$ 

(ii) \[{{\mathbf{I}}_{{\mathbf{y}}{\mathbf{R}}}}/{{\mathbf{I}}_{{\mathbf{y}}{\mathbf{S}}}} > {\mathbf{1}}\]

Ans: $\dfrac{{{I_{yR}}}}{{{I_{ys}}}} = \dfrac{{m{{\left( {\dfrac{a}{2}} \right)}^2}}}{{m{{\left( {\dfrac{c}{2}} \right)}^2}}} = \dfrac{{{a^2}}}{4} \cdot \dfrac{4}{{{c^2}}} = \dfrac{{{a^2}}}{{{c^2}}}$

$\because a > c \Rightarrow \dfrac{{{a^2}}}{{{c^2}}} > 1$

$\dfrac{{{I_{yR}}}}{{{I_{ys}}}} > 1$ 

(iii) \[{{\mathbf{I}}_{{\mathbf{z}}{\mathbf{R}}}}/{{\mathbf{I}}_{{\mathbf{z}}{\mathbf{S}}}} > {\mathbf{1}}\]

Ans: Lets start,

${I_{zR}} - {L_{zs}} = m{\left( {\dfrac{{{d_R}}}{2}} \right)^2} - m{\left( {\dfrac{{ds}}{2}} \right)^2}$

${I_{zR}} - {I_{zS}} = \dfrac{m}{4}\left[ {d_R^2 - d_S^2} \right] = \dfrac{m}{4}\left[ {{a^2} + {b^2} - 2{c^2}} \right]$

$\therefore {I_{zR}} - {I_{zS}} = \dfrac{m}{4}\left( {{a^2} + {b^2} - 2ab} \right) = \dfrac{m}{4}{(a - b)^2}\left( {{c_2} = ab} \right)$

$\therefore {I_{zR}} - {I_{zS}} > 0$

$\because \dfrac{m}{4}{(a - b)^2} > 0$

$\Rightarrow \dfrac{{{I_{zR}}}}{{{I_{zS}}}} > 1$ 

7.28 A uniform disc of radius R, is resting on a table on its rim. The coefficient of friction between disc and table is $\mu$ (Fig 7. 12). Now the disc is pulled with a force ${\mathbf{F}}$ as shown in the figure. What is the maximum value of ${\mathbf{F}}$ for which the disc rolls without slipping?

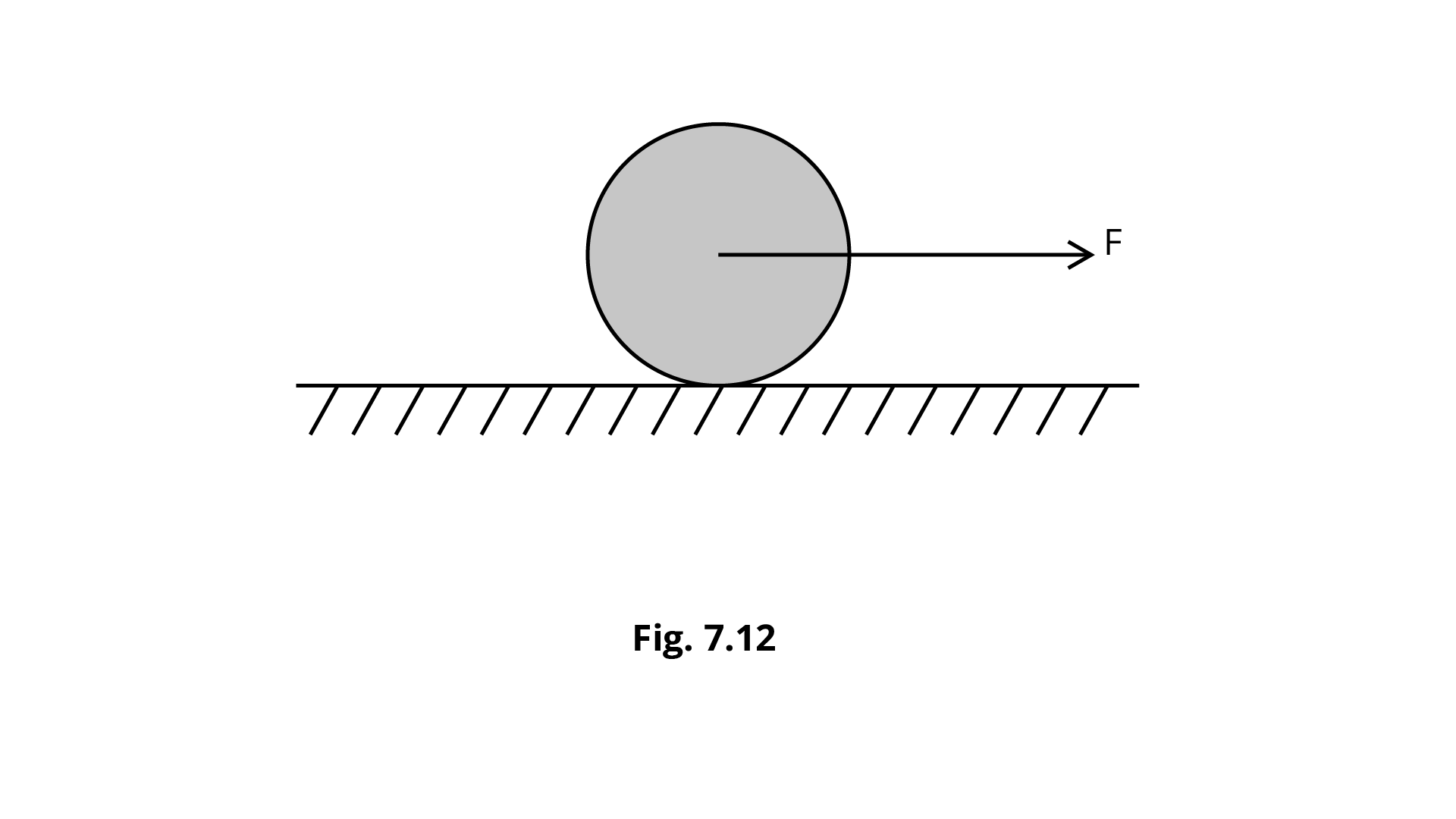
Ans: Assume that,

$a = $ linear acceleration

$\alpha  = $ angular acceleration

$F - f = Ma \ldots {\text{ (i) }}$

Torque on disc $\tau  = {I_D}\alpha $

M.I. ${I_D} = \dfrac{1}{2}M{R^2}$

$f \cdot R = \dfrac{1}{2}M{R^2} \cdot \dfrac{a}{R}\quad \because a = Ra$

$fR = \dfrac{1}{2}MRa \Rightarrow Ma = 2f\quad  \ldots {\text{ (ii) }}$

$F - f = 2f$

$3f = F{\text{ or }}f = \dfrac{F}{3}$

$\because N = Mg$

$\mu  \cdot M = \dfrac{F}{3}{\text{ or }}\mu Mg = \dfrac{F}{3}$ 

As a result, max. force applied on disc $F = 3\mu {\text{Mg}}$.