NCERT Exemplar for Class 11 Physics Chapter 4 - Motion in a Plane (Book Solutions)

Exercise

MULTIPLE CHOICE QUESTIONS (TYPE - I)

4.1. The angle between $\overrightarrow A  = \widehat i + \widehat j$ and $\overrightarrow B  = \widehat i - \widehat j$ is

(a) 45⁰

(b) 90⁰

(c) -45⁰

(d) 180⁰

Ans: Option (b) 

Since we know that, the angle between two vectors is given by

$ \Rightarrow \cos \theta  = \dfrac{{\overrightarrow A  \cdot \overrightarrow B }}{{\left| A \right|\left| B \right|}}$

Hence,

$ \Rightarrow \cos \theta  = \dfrac{{1 - 1}}{{\sqrt 2  \cdot \sqrt 2 }} = \dfrac{0}{2} = 0$

i.e.

$ \Rightarrow \theta  = 90^\circ $

Hence, the correct answer is (b).

4.2. Which one of the following statements is true?

(a) A scalar quantity is the one that is conserved in a process.

(b) A scalar quantity is the one that can never take negative values.

(c) A scalar quantity is the one that does not vary from one point to another in space.

(d) A scalar quantity has the same value for observers with different orientations of the axes.

Ans: Option (d) 

A scalar quantity has no direction hence it is the same when observed with different orientations of the axes. Hence, the correct answer is (d).

4.3. Figure shows the orientation of two vectors $\overrightarrow u $ and $\overrightarrow v $ in the X-Y plane.

If $\overrightarrow u  = a\widehat i + b\widehat j$ and $\overrightarrow v  = p\widehat i + q\widehat j$ ,

Which of the following is correct?

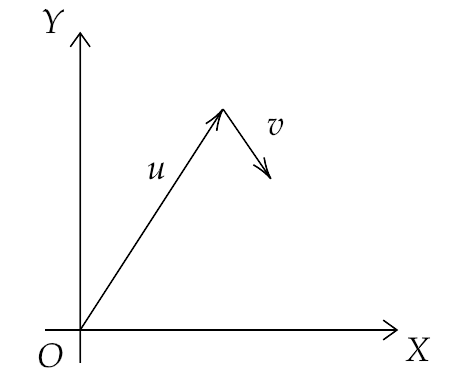
(a) a and p are positive while b and q are negative.

(b) a, p and b are positive while q is negative.

(c) a, q and b are positive while p is negative.

(d) a, b, p and q are all positive.

Ans: Option (b) 

Since a, b and p, q are the components of X and Y direction and we can see that the second vector moving down and forwards, hence the Y-component of vector $\overrightarrow v $ , i.e. q is negative. The rest are positive. Hence, the correct answer is (b).

4.4. The component of vector r along X-axis will have maximum value if:

(a) $\overrightarrow r $ is along the positive Y-axis.

(b) $\overrightarrow r $ is along the positive X-axis.

(c) $\overrightarrow r $ makes an angle of 45⁰ with X-axis.

(d) $\overrightarrow r $ is along the negative Y-axis.

Ans: Option (b) 

Since the value of $\cos {\theta _{\max }} = 1$ occurs when $\theta  = 0^\circ $ , therefore  it can happen only when $\overrightarrow r $ is along the positive X-axis. Hence, the correct answer is (b).

4.5. The horizontal range of a projectile fired at an angle of 15⁰ is 50m. If it is fired with the same at an angle of 45⁰, its range will be:

(a) 60 m

(b) 71 m

(c) 100 m

(d) 141 m

Ans: Option (c) 

Given that the horizontal range is 50m.

Therefore, we have

$ \Rightarrow R = \dfrac{{{u^2}\sin 2\theta }}{g}$

Hence,

$ \Rightarrow 50 = \dfrac{{{u^2}\sin 2 \times 15^\circ }}{g}$

That gives,

$ \Rightarrow {u^2} = 100g$

Now if we have $\theta  = 45^\circ $ , then

$ \Rightarrow R = \dfrac{{{u^2}\sin 2\theta }}{g} = \dfrac{{100g \cdot \sin 2 \times 45^\circ }}{g} = 100m$

Hence, the correct answer is (c).

4.6. Consider the quantities, pressure, power, energy impulse, gravitational potential, electric charge, temperature, area. Out of these, the only vector quantities are:

(a) Impulse, pressure and area

(b) Impulse and area

(c) Area and gravitational constant

(d) Impulse and pressure

Ans: Option (b) 

In the above given quantities only energy impulse and area are vector quantities and the rest are scalar quantities as they have no direction. Hence, the correct answer is (b).

4.7. In a two dimensional motion, instantaneous speed vₒ is positive, constant. Then which of the following are necessarily true?

(a) The average velocity is not zero at any time.

(b) Average acceleration must always vanish.

(c) Displacements in equal time intervals are equal.

(d) Equal path lengths are traversed in equal intervals.

Ans: Option (d) 

If the instantaneous speed vₒ is positive and constant in a two dimensional motion, then due to the scalar nature of speed equal path lengths are traversed in equal intervals. Hence, the correct answer is (d).

4.8. In a two-dimensional motion, instantaneous speed $v_0$ is positive and constant. Then which of the following are necessarily true?

(a) The acceleration of a particle is zero.

(b) The acceleration of the particle is bounded.

(c) The acceleration of the particle is necessarily in the plane of motion.

(d) The particle must be undergoing a uniform circular motion.

Ans: Option (c) 

The acceleration of the particle will necessarily be zero and in the plane of motion because the given speed is constant and positive, i.e. in the direction of force. Hence, the correct answer is (c).

4.9. Three vectors $\overrightarrow A $ , $\overrightarrow B $ and $\overrightarrow C $ add up to zero. Find which is false.

(a) $\left( {\overrightarrow A  \times \overrightarrow B } \right) \times \overrightarrow C $ is not zero unless $\overrightarrow B {\text{ and }}\overrightarrow C $ are parallel.

(b) $\left( {\overrightarrow A  \times \overrightarrow B } \right) \cdot \overrightarrow C $ is not zero unless $\overrightarrow B {\text{ and }}\overrightarrow C $ are parallel.

(c) If $\overrightarrow A $ , $\overrightarrow B $ and $\overrightarrow C $ define a place, $\left( {\overrightarrow A  \times \overrightarrow B } \right) \times \overrightarrow C $ is in that plane.

(d) $\left( {\overrightarrow A  \times \overrightarrow B } \right) \cdot \overrightarrow C  = \left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right| \geqslant \left| {\overrightarrow C } \right| \Rightarrow {C^2} = {A^2} + {B^2}$

Ans: Options (b) and (d) 

Given that, $\overrightarrow A  + \overrightarrow B  + \overrightarrow C  = 0$

Now for (a), we can write

$ \Rightarrow \overrightarrow B  \times \left( {\overrightarrow A  + \overrightarrow B  + \overrightarrow C } \right) = \overrightarrow {\rm B}  \times 0$

$ \Rightarrow \overrightarrow B  \times \overrightarrow A  + \overrightarrow B  \times \overrightarrow B  + \overrightarrow B  \times \overrightarrow C  = 0$

i.e.

$ \Rightarrow \overrightarrow B  \times \overrightarrow A  + 0 + \overrightarrow B  \times \overrightarrow C  = 0$

That gives us,

$ \Rightarrow \overrightarrow B  \times \overrightarrow A  =  - \overrightarrow B  \times \overrightarrow C $

Hence,

$ \Rightarrow \overrightarrow A  \times \overrightarrow B  = \overrightarrow B  \times \overrightarrow C $

Now, that gives us,

$ \Rightarrow \left( {\overrightarrow A  \times \overrightarrow B } \right) \times \overrightarrow C  = \left( {\overrightarrow B  \times \overrightarrow C } \right) \times \overrightarrow C $

Now if $\overrightarrow B {\text{ and }}\overrightarrow C $ are parallel or antiparallel, then we have

$ \Rightarrow \left( {\overrightarrow A  \times \overrightarrow B } \right) \times \overrightarrow C  = \left| {BC\sin 0^\circ } \right| \times \overrightarrow C $

i.e.

$ \Rightarrow \left( {\overrightarrow A  \times \overrightarrow B } \right) \times \overrightarrow C  = 0$

So option (a) is true.

Option (b) is false because $\left( {\overrightarrow A  \times \overrightarrow B } \right) \cdot \overrightarrow C $ is always zero without $\overrightarrow B {\text{ and }}\overrightarrow C $ being parallel if we take $\overrightarrow A  \times \overrightarrow B  = \overrightarrow B  \times \overrightarrow C  = \overrightarrow P $ then we have $\overrightarrow P  \cdot \overrightarrow C  = 0$ because both vectors are perpendicular.

Now for option (c), if we have  $\overrightarrow A $ , $\overrightarrow B $ and $\overrightarrow C $ in the same plane,   $\left( {\overrightarrow A  \times \overrightarrow B } \right)$ will be perpendicular to that plane, and then the vector $\left( {\overrightarrow A  \times \overrightarrow B } \right) \times \overrightarrow C $ will be perpendicular to both $\left( {\overrightarrow A  \times \overrightarrow B } \right)$ and $\overrightarrow C $ and hence the vector  $\left( {\overrightarrow A  \times \overrightarrow B } \right) \times \overrightarrow C $ will lie in the original plane containing $\overrightarrow A $ , $\overrightarrow B $ and $\overrightarrow C $. So option (c) is true. 

For option (d) we have ${C^2} = {A^2} + {B^2}$

That means the angle between $\overrightarrow A $ and $\overrightarrow B $ is $90^\circ $ .

Now, we can write,

$ \Rightarrow \left( {\overrightarrow A  \times \overrightarrow B } \right) \cdot \overrightarrow C  = \left( {\left| A \right|\left| B \right|\sin 90^\circ } \right) \cdot \overrightarrow C $

That gives us,

$ \Rightarrow \left( {\overrightarrow A  \times \overrightarrow B } \right) \cdot \overrightarrow C  = \left| A \right|\left| B \right|\left| C \right|\cos \theta $

But

$ \Rightarrow \left( {\overrightarrow A  \times \overrightarrow B } \right) \cdot \overrightarrow C  = \left| A \right|\left| B \right|\left| C \right|\cos \theta  \ne \left| A \right|\left| B \right|\left| C \right|$

So option (d) is false.

Hence, the correct answers are (b) and (d).

4.10. It is found that $\left| {\overrightarrow A  + \overrightarrow B } \right| = \left| {\overrightarrow A } \right|$ , this necessarily implies

(a) $\overrightarrow B  = 0$

(b) $\overrightarrow A ,\overrightarrow B $ are anti-parallel

(c) $\overrightarrow A ,\overrightarrow B $ are perpendicular

(d) $\overrightarrow A  \cdot \overrightarrow B  \leqslant 0$

Ans: Options (a) and (d)

Given that, $\left| {\overrightarrow A  + \overrightarrow B } \right| = \left| {\overrightarrow A } \right|$

That gives us, $\left| {\overrightarrow A  + \overrightarrow B } \right| = \left| {\overrightarrow A  + 0} \right|$

Hence, $\overrightarrow B  = 0$

So the option (a) is correct.

Now if $\overrightarrow A ,\overrightarrow B $ are anti-parallel, then we can write $\overrightarrow B  =  - k\overrightarrow A $

Then, we have

$ \Rightarrow \left| {\overrightarrow A  + \overrightarrow B } \right| = \left| {\overrightarrow A  - k\overrightarrow A } \right|$

$ \Rightarrow \left| {\overrightarrow A  + \overrightarrow B } \right| = \left| {1 - k} \right|\left| {\overrightarrow A } \right|$

Now $\left| {1 - k} \right|\left| {\overrightarrow A } \right|$ is not necessarily equal to $\left| {\overrightarrow A } \right|$ , hence option (b) is wrong.

Also if $\overrightarrow A ,\overrightarrow B $ are perpendicular, then we have the magnitude of the resultant vector always greater than that of the two vectors i.e. $\left| {\overrightarrow A  + \overrightarrow B } \right| > \left| {\overrightarrow A } \right|$ and $\left| {\overrightarrow A  + \overrightarrow B } \right| > \left| {\overrightarrow B } \right|$

Hence, option (c) is wrong.

Now if $\left| {\overrightarrow A  + \overrightarrow B } \right| = \left| {\overrightarrow A } \right|$

Then we have

$ \Rightarrow {\left| {\overrightarrow A } \right|^2} + {\left| {\overrightarrow B } \right|^2} + 2\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right| = {\left| {\overrightarrow A } \right|^2}$

$ \Rightarrow \left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right| =  - \dfrac{{{{\left| {\overrightarrow B } \right|}^2}}}{2}$

Hence, $ \Rightarrow \left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right| \leqslant 0$

So option (d) is correct.

Hence, the correct answer is option (a) and (d).

MULTIPLE CHOICE QUESTIONS-II

4.11. Two particles are projected in air with speed vₒ at angles ${\theta _1}$ and ${\theta _2}$ (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than of the second, then tick the right choices

(a) angle of projection: ${\theta _1} > {\theta _2}$

(b) time of flight: T1>T2

(c) horizontal range: R1>R2

(d) total energy: U1<U2

Ans: Options (a) and (b) 

Given that, ${h_1} > {h_2}$

Hence, $\dfrac{{{v_0}^2{{\sin }^2}{\theta _1}}}{{2g}} > \dfrac{{{v_0}^2{{\sin }^2}{\theta _2}}}{{2g}}$

That gives, ${\sin ^2}{\theta _1} > {\sin ^2}{\theta _2}$

${\theta _1} > {\theta _2}$

Also, the ratio of time of flight is $\dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{2{v_0}\sin {\theta _1}/g}}{{2{v_0}\sin {\theta _2}/g}} = \dfrac{{\sin {\theta _1}}}{{\sin {\theta _2}}}$

Since $\sin {\theta _1} > \sin {\theta _2}$ hence ${T_1} > {T_2}$

And the ratio of their horizontal range is,

$ \Rightarrow \dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{v_0}^2\sin 2{\theta _1}}}{g} \times \dfrac{g}{{{v_0}^2\sin 2{\theta _2}}}$

Or,

$ \Rightarrow \dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{\sin 2{\theta _1}}}{{\sin 2{\theta _2}}}$

That gives us,

$ \Rightarrow \dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{2\sin {\theta _1}\cos {\theta _1}}}{{2\sin {\theta _2}\cos {\theta _2}}}$

Since ${\theta _1} > {\theta _2}$ hence ${R_1} > {R_2}$

But if ${\theta _1} + {\theta _2} = 90^\circ $ then  ${R_1} = {R_2}$

Also, the total energy of the two given particles for this motion depends on their respective masses, and since the relation between their masses is not given hence we can not determine the relation between their total energies.

Hence, the correct answers are (a) and (b).

4.12. A particle slides down a frictionless parabolic ($y = {x^2}$  ) track (A – B – C) starting from rest at point A as in figure. Point B is at the vertex of parabola and point C is at a height less than that of point A. After c, the particle moves freely in air as a projectile. If the particle reaches highest point at P, then

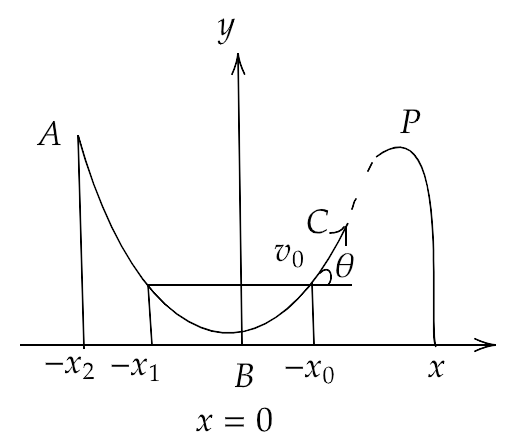
(a) KE at p= KE at B

(b) height at p = height at A

(c) total energy at p= total energy at A

(d) time of travel from A to B =time of travel from B to P.

Ans: Option (c) 

(a) Since the kinetic energy of the particle will be maximum at the point B, hence the K.E. at point B will be greater than the K.E. at point P.

(b) Since the potential energy of the particle will be maximum at the point A, hence the height at point A will be greater than the height at point P.

(c) As the path ABC is frictionless of air and plane, therefore the total energy of the particle will remain unchanged at any point throughout the journey and is equal at the point A and P.

(d) Since the path from A to B is greater than the path from B to P, therefore the time of travel from A to B is greater than the time of travel from B to P.

Hence, the correct answer is (c).

4.13. Following are four different relations about displacement, velocity and acceleration for the motion of a particle in general. Choose the incorrect one(s).

(a) ${\overrightarrow v _{av}} = \dfrac{1}{2}\left[ {\overrightarrow v \left( {{t_1}} \right) + \overrightarrow v \left( {{t_2}} \right)} \right]$

(b) ${\overrightarrow v _{av}} = \dfrac{{\overrightarrow r \left( {{t_2}} \right) - \overrightarrow r \left( {{t_1}} \right)}}{{{t_2} - {t_1}}}$

(c) $\overrightarrow r  = \dfrac{1}{2}\left[ {\overrightarrow v \left( {{t_2}} \right) - \overrightarrow v \left( {{t_1}} \right)} \right] \div \left( {{t_2} - {t_1}} \right)$

(d) ${\overrightarrow a _{av}} = \dfrac{{\overrightarrow v \left( {{t_2}} \right) - \overrightarrow v \left( {{t_1}} \right)}}{{\left( {{t_2} - {t_1}} \right)}}$

Ans: Options (a) and (c) 

The first condition ${\overrightarrow v _{av}} = \dfrac{1}{2}\left[ {\overrightarrow v \left( {{t_1}} \right) + \overrightarrow v \left( {{t_2}} \right)} \right]$ is possible if and only if the given acceleration is uniform but not otherwise.

Also, the dimensions in the third conditions are not equal in the LHS and RHS.

Therefore, the correct answers are (a) and (c).

4.14. For a particle performing uniform circular motion, choose the correct statement(s) from the following:

(a) Magnitude of particle velocity (speed) remains constant.

(b) Particle velocity remains directed perpendicular to the radius vector.

(c) Direction of acceleration keeps changing as the particle moves.

(d) Angular momentum is constant in magnitude but direction keeps changing.

Ans: Options (a), (b) and (C) 

In a uniform circular motion, the velocity is constant in the tangential direction and the direction of acceleration keeps changing at every instant of motion.

(a) Since the motion is uniform, hence the magnitude of velocity remains constant.

(b) As the direction of the velocity is tangential throughout the circular motion, so it is perpendicular to the radius vector.

(c) The acceleration of a particle moving in a uniform circular motion is always directed towards the centre. Therefore, at every point of the motion, the direction of the acceleration keeps changing in order to be directed towards the centre.

(d) Since the velocity and the radius vector remains constant in a uniform circular motion, therefore the angular momentum $\overrightarrow L  = m\left( {\overrightarrow v  \times \overrightarrow r } \right)$ also remains constant. Also the direction of the angular momentum is always constant and perpendicular towards the plane containing the velocity and radius vectors.

Hence, the correct answers are (a), (b) and (c) and option (d) is wrong.

4.15. For two vectors $\overrightarrow A $ and $\overrightarrow B $ , $\left| {\overrightarrow A  + \overrightarrow B } \right| = \left| {\overrightarrow A  - \overrightarrow B } \right|$ is always true when

(a) $\left| {\overrightarrow A } \right| = \left| {\overrightarrow B } \right| \ne 0$

(b) $\overrightarrow A  \bot \overrightarrow B $

(c) $\left| {\overrightarrow A } \right| = \left| {\overrightarrow B } \right| \ne 0$ and $\overrightarrow A $ and $\overrightarrow B $ are parallel or anti-parallel

(d) Either $\left| {\overrightarrow A } \right|{\text{ or }}\left| {\overrightarrow B } \right|$ is zero

Ans: Options (b) and (d) 

Given that $\left| {\overrightarrow A  + \overrightarrow B } \right| = \left| {\overrightarrow A  - \overrightarrow B } \right|$

That gives, ${\left| {\overrightarrow A  + \overrightarrow B } \right|^2} = {\left| {\overrightarrow A  - \overrightarrow B } \right|^2}$

${\left| {\overrightarrow A } \right|^2} + {\left| {\overrightarrow B } \right|^2} + 2\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\cos \theta  = {\left| {\overrightarrow A } \right|^2} + {\left| {\overrightarrow B } \right|^2} - 2\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\cos \theta $

That is, $4\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\cos \theta  = 0$

Therefore, either $\left| {\overrightarrow A } \right|{\text{ or }}\left| {\overrightarrow B } \right|$ is zero or $\theta  = 90^\circ $ i.e. $\overrightarrow A  \bot \overrightarrow B $

Hence, the correct answers are (b) and (d).

VERY SHORT ANSWER TYPE QUESTIONS

4.16. A cyclist starts from centre O of a circular park of radius 1 Km and moves along the path OPRQO as shown in the figure. If he maintains the constant speed of 10m/s, what is his acceleration at point R in magnitude and direction?

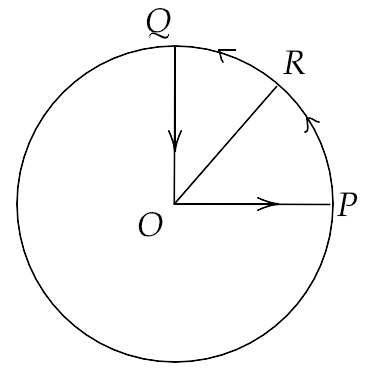
Ans: His acceleration at point R will be given by $a = \dfrac{{{v^2}}}{r}$

That gives, $a = \dfrac{{100{m^2}{s^{ - 2}}}}{{1000m}} = 0.1\,m{s^{ - 2}}$

The direction of the acceleration will be along RO.

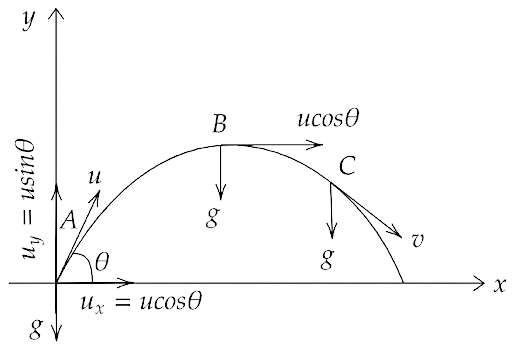
4.17. A particle is projected in the air at some angle to the horizontal, moves along the parabola as shown in the figure, where x and y indicate horizontal and vertical directions respectively. Show in the diagram, direction of velocity and acceleration at points A, B and C.

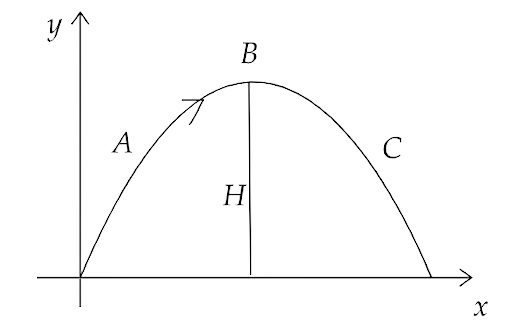
Ans: The direction of velocity is always tangential towards the direction of motion at any point of the trajectory. And since , in the given figure point B is maximum height of trajectory, hence the vertical component of B is zero and the horizontal component is $u\cos \theta $.

Also at the points A and C, gravitational acceleration $g$ is acting downwards. Hence, the direction of velocity and acceleration at points A, B and C is shown in the figure below.

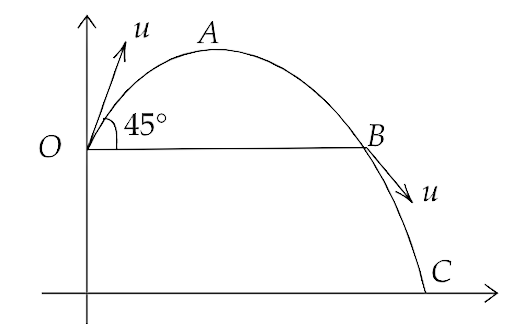
4.18. A ball is thrown from a rooftop at an angle of 45⁰ above the horizontal. It hits the ground a few seconds later. At what point during its motion, does the ball have

(a) greatest speed

Ans: The  path of the ball can be shown by the figure given below:

Now,

(a) The maximum speed of the ball will be at point C, given by ${v_y}$ as maximum and ${v_x} = u\cos 45^\circ  = \dfrac{u}{{\sqrt 2 }}$

(b) smallest speed

Ans: The minimum speed will be at the maximum height B where ${v_y}$ is zero and ${v_x} = \dfrac{u}{{\sqrt 2 }}$

(c) greatest acceleration? Explain.

Ans: Since the force acting on the ball is gravitational force only, hence the acceleration of the ball is always downwards and equal to $g$ .

4.19. A football is kicked into the air vertically upwards. What is its 

(a) Acceleration, and 

Ans: Since the football is kicked vertically upwards and the only acting force on the ball is the gravitational force. Hence, the acceleration at every point of trajectory of the ball is $g$ .

(b) Velocity at the Highest Point?

Ans: The velocity of the football at the highest point will be zero because both components of its velocity will be equal to zero at the highest point.

4.20. A, B and C are three non-collinear, non-co-planar vectors. What can you say about the direction of $\overrightarrow A  \times \left( {\overrightarrow B  \times \overrightarrow C } \right)$ ?

Ans: Using the right-hand thumb rule we can say that the vector $\left( {\overrightarrow B  \times \overrightarrow C } \right)$ will be perpendicular to the plane which have the vectors $\overrightarrow B $ and $\overrightarrow C $ . Then again, the direction of $\overrightarrow A  \times \left( {\overrightarrow B  \times \overrightarrow C } \right)$ will be perpendicular to $\overrightarrow A $ and in the plane containing the two vectors $\overrightarrow B $ and $\overrightarrow C $ .

SHORT ANSWER TYPE QUESTIONS

4.21. A boy travelling in an open car moving on a levelled road with constant speed tosses a ball vertically up in the air and catches it back. Sketch the motion of the ball as observed by a boy standing on the footpath. Give an explanation to support your diagram.

Ans: Let the vertical velocity of the tossed ball be v and speed of the car be u which must be equal to the horizontal velocity of the ball.

The ball has both components of motion, hence it will have a parabolic trajectory when observed from a distance. This can be shown by the figure below.

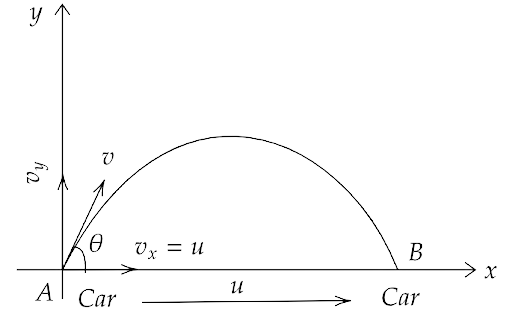
When this motion is observed by the boy sitting in the car, it will look like only a vertically up-down motion and he will catch the ball when it comes back to the ground if the car has a constant velocity.

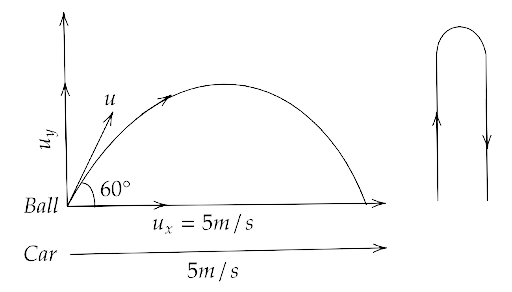
4.22. A boy throws a ball in the air at 60⁰ to the horizontal along a road with a speed of 10 m/s (36 km/h). Another boy sitting in a passing by car observes the ball. Sketch the motion of the ball as observed by the boy in the car, if the car has a speed of (18 km/h). Give an explanation to support your diagram.

Ans: Given that, the initial velocity of the ball $u = 10m/s$

That gives, ${u_x} = u\cos 60^\circ  = 10 \cdot \dfrac{1}{2} = 5m/s$

Velocity of car is in the direction of ${u_x}$ and equal to $18 \cdot \dfrac{5}{{18}} = 5m/s$ 

Now since they have equal horizontal velocity hence they will cover equal distances when the ball comes down. But, the ball also has a vertical velocity of ${u_y} = u\cos 30^\circ  = 10 \cdot \dfrac{{\sqrt 3 }}{2} = 5\sqrt {3m/s} $ hence it travels upwards in a parabolic trajectory.

When observed by the car, this motion will look like a simple vertical up-down motion as shown below.

4.23. In dealing with the motion of a projectile in the air, we ignore the effect of air resistance on the motion. This gives the trajectory as a parabola as you have studied. What would the trajectory look like if air resistance is included? sketch such a trajectory and explain why you have drawn it that way.

Ans: If the air resistance is included in a parabolic trajectory then both the horizontal and vertical speed of the particle will decrease due to that resistance. This will result in a decrease in the maximum attained height and in the range achieved by the particle. These two conditions can be compared by the figure drawn below:

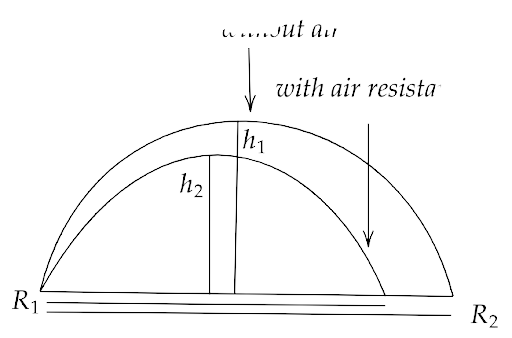
4.24. A fighter plane is flying horizontally at an altitude of 1.5 km with speed 720 km/h. At What angle of sight (w.r.t horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target?

Ans: The velocity of the fighter plane at a height $h = 1.5\,km = 1500\,m$ is given as $u = 720\,km/h = 720 \cdot \dfrac{5}{{18}} = 200\,m/s$

Let the plane drops the bomb t seconds before the target is exactly below the plane.

Then in t seconds, the bomb must cover the vertical distance of 1500m under free fall with initial velocity zero.

Hence, $h = ut + \dfrac{1}{2}g{t^2}$

That gives, $1500 = 0 + \dfrac{1}{2}10{t^2}$

$t = \sqrt {300}  = 10\sqrt 3 s$

Now distance covered by the plane is $ut = 200 \times 10\sqrt 3  = 2000\sqrt 3 $

Hence, $\tan \theta  = \dfrac{{1500}}{{2000\sqrt 3 }} = \dfrac{{\sqrt 3 }}{4}$

Therefore, $\theta  = {\tan ^{ - 1}}\dfrac{{\sqrt 3 }}{4} = 23^\circ 42'$

4.25. (a) Earth can be thought of as a sphere of radius 6400 km. Any object (or a person) is performing circular motion around the axis of the earth due to earth’s rotation (period 1 day). What is the acceleration of an object on the surface of earth (at equator) towards its center? What is it at latitude $\theta $ ? How do these accelerations compare with $g = 9.8\,m/{s^2}$ ?

Ans: The angular acceleration towards the centre in a circular motion is given by, $a = \dfrac{{{v^2}}}{R} = \dfrac{{{\omega ^2}{R^2}}}{R} = {\omega ^2}R$

Here, $\omega  = \dfrac{{2\pi }}{T}$ and $T = 24 \times 3600s$

Now the acceleration of the person on the surface of earth towards the centre of earth is given by, $a = {\omega ^2}R = {\left( {\dfrac{{2\pi }}{T}} \right)^2}R = \dfrac{{4{\pi ^2}R}}{{{T^2}}}$

That gives, $a = \dfrac{{4 \times 22 \times 22 \times 6.4 \times {{10}^6}}}{{7 \times 7 \times 24 \times 24 \times 3600 \times 3600}} = 0.034m/{s^2}$

Now at equator, i.e. latitude $\theta  = 0^\circ $

Acceleration compared with $g = 9.8m/{s^2}$ is $\dfrac{a}{g} = \dfrac{{0.034}}{{9.8}} = \dfrac{1}{{288}}$ which is a very small quantity

(b) Earth also moves in circular orbit around the sun once every year with an orbital radius of $1.5 \times {10^{11}}m$ . What is the acceleration of earth (or any object on the surface of the earth) towards the center of the sun? How does this acceleration compare with $g = 9.8m/{s^2}$ .

Ans: For the revolution of earth around the sun we have,

$R = 1.5 \times {10^{11}}m$ and $T = 365 \times 24 \times 3600 = 3.15 \times 1{0^7}s$

Since, $a = {\omega ^2}R = {\left( {\dfrac{{2\pi }}{T}} \right)^2}R = \dfrac{{4{\pi ^2}R}}{{{T^2}}}$

Hence, $a = \dfrac{{4 \times 3.14 \times 3.14 \times 1.5 \times {{10}^{11}}}}{{3.15 \times 3.15 \times {{10}^7} \times {{10}^7}}} \approx 6 \times 1{0^{ - 3}}m/{s^2}$

Comparing this acceleration with $g = 9.8m/{s^2}$ we have $\dfrac{a}{g} = \dfrac{{6 \times 1{0^{ - 3}}}}{{9.8}} = \dfrac{1}{{1633}}$

4.26. Given below in column I are the relations between vectors $\overrightarrow a ,\overrightarrow b {\text{ and }}\overrightarrow c $ and in column II are the orientations of $\overrightarrow a ,\overrightarrow b {\text{ and }}\overrightarrow c $ in the X-Y plane. Match the relation in column I to correct orientations in column II.

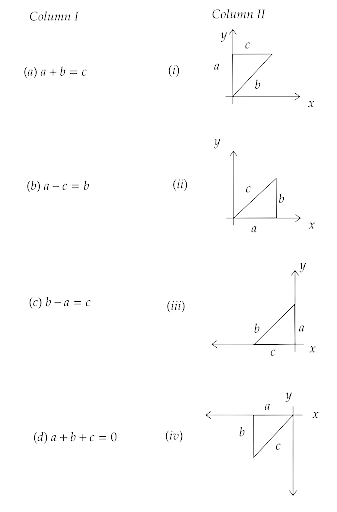
Ans: The correct match for the elements of column I and II are as follows:

4.27. If $\left| A \right| = 2$ and $\left| B \right| = 4$ , then match the relations in column I with the angle $\theta $ between A and B in column II.

Ans: (a) $\overrightarrow A  \cdot \overrightarrow B  = 0$

This gives us $\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\cos \theta  = 0$

i.e., $\cos \theta  = 0$

Hence, $\theta  = 90^\circ $

(b) $\overrightarrow A  \cdot \overrightarrow B  =  + 8$

This gives us $\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\cos \theta  = 8$

Since, $\left| A \right| = 2$ and $\left| B \right| = 4$, so we get, $\cos \theta  = 1$

Hence, $\theta  = 0^\circ $

(c) $\overrightarrow A  \cdot \overrightarrow B  = 4$

This gives us $\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\cos \theta  = 4$

Since $\left| A \right| = 2$ and $\left| B \right| = 4$, so we get $\cos \theta  = \dfrac{1}{2}$

Hence, $\theta  = 60^\circ $

(d) $\overrightarrow A  \cdot \overrightarrow B  =  - 8$

This gives us $\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\cos \theta  =  - 8$

Since, $\left| A \right| = 2$ and $\left| B \right| = 4$ so we get $\cos \theta  =  - 1$

Hence, $\theta  = 180^\circ $

Hence, the correct match for the elements of column I and II are as follows:

4.28. If $\left| A \right| = 2$ and $\left| B \right| = 4$ Then match the relations in column I with the angle $\theta $ between A and B in column II.

Ans: (a) $\left| {\overrightarrow A  \times \overrightarrow B } \right| = 0$

This gives us $\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\sin \theta  = 0$

i.e., $\sin \theta  = 0$

Hence, $\theta  = 0^\circ $

(b) $\left| {\overrightarrow A  \times \overrightarrow B } \right| = 8$

This gives us $\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\sin \theta  = 8$

Since | A | = 2 and | B| = 4, so we get, $\sin \theta  = 1$

Hence, $\theta  = 90^\circ $

(c) $\left| {\overrightarrow A  \times \overrightarrow B } \right| = 4$

This give us $\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\sin \theta  = 4$

Since $\left| A \right| = 2$ and $\left| B \right| = 4$, so we get $\sin \theta  = \dfrac{1}{2}$

Hence,$\theta  = 30^\circ $

(d) $\left| {\overrightarrow A  \times \overrightarrow B } \right| = 4\sqrt 2 $

This gives us $\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\sin \theta  = 4\sqrt 2 $

Since, $\left| A \right| = 2$ and $\left| B \right| = 4$, so we get $\sin \theta  = \dfrac{1}{{\sqrt 2 }}$

Hence, $\theta  = 45^\circ $

Hence, the correct match for the elements of column I and II are as follows:

LONG ANSWER TYPE QUESTIONS

4.29. A hill is 500 m high. Supplies are to be sent across the hill using a canon that can hurl packets at a speed of 125 m/s over the hill. The cannon is located at a distance of 800 m from the foot of the hill and can be moved on the ground at a speed of 2 m/s; so that its distance from the hill can be adjusted. What is the shortest time in which a packet can reach the ground across the hill? Take $g = 10\,m/{s^2}$ .

Ans: We are given that the speed of packets is 125 m/s  and the height of the hill is 500 m.

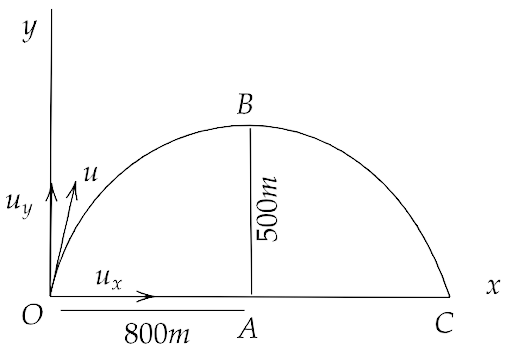
Now, in order to cross the hill by packet, the vertical components of the speed of packet must be reduced so that it can attain a height of 500 m and the distance between the hill and the cannon must be half of the range of the packet.

Hence, 

$ \Rightarrow {v^2} = {u^2} + 2gh$

$ \Rightarrow 0 = {u_y}^2 - 2gh$

That gives, $ \Rightarrow {u_y}^2 = \sqrt {2gh}  = \sqrt {2 \times 10 \times 500}  = 100m/s$

Now, we have 

$ \Rightarrow {u^2} = {u_x}^2 + {u_y}^2$

Hence, ${u_x}^2 = {125^2} - {100^2} = 25 \times 125$

i.e. ${u_x} = 5 \times 15 = 75m/s$

Now, the vertical motion of the packet is given by ${v_y} = {u_y} + gt$ i.e. $0 = 100 - 10t$ or $t = 10s$

Hence, the time of half flight and time to reach the top of the hill is 10 seconds.

Therefore the cannon must be at the half range i.e. at the horizontal distance in 10 sec

Hence the distance between the hill and the canon is given by ${u_x} \times 10 = 75 \times 10 = 750m$

Therefore the required distance for the cannon is $800 - 750 = 50m$

Time taken by the cannon to cover 50m is $\dfrac{{50}}{2} = 25s$

Therefore, the total time taken by the packet from 800 m away from the hill to reach the other side of the hill is equal to $25 + 10 + 10 = 45s$ .

4.30. A gun can fire shells with maximum speed ${v_0}$ and the maximum horizontal range that can be achieved is $R = \dfrac{{{v_0}^2}}{g}$ . If a target farther away by distance $\Delta x$ (beyond R) has to be hit with the same gun as shown in the figure here. Show that it could be achieved by raising the gun to a height at least $h = \Delta x\left[ {1 + \dfrac{{\Delta x}}{R}} \right]$

Hint: This problem can be approached in two different ways:

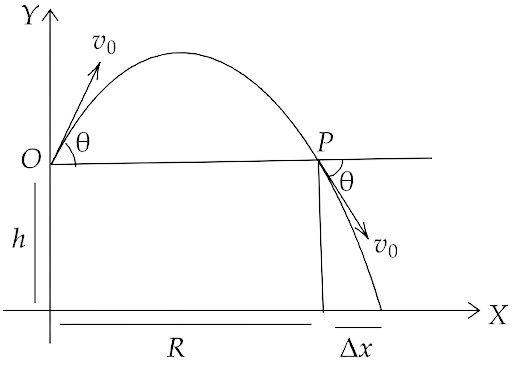
(i) Refer to the diagram: target T is at the horizontal distance $x = R + \Delta x$ and below the point of projection y=-h.

(ii) From point P in the diagram: Projection at speed ${v_0}$ at an angle $\theta $ below horizontal with height h and horizontal range $\Delta x$ .

Ans: The maximum horizontal range is given as $R = \dfrac{{{v_0}^2}}{g}$

That means the angle of projection must be $\theta  = 45^\circ $

If the gun is raised to a height h from the horizontal level of target T so that the projectile can hit the target T,

Then the total range of the projectile must be $x = R + \Delta x$

Also the horizontal component of velocity at the point A will be given by ${v_0}\cos \theta $

Now, the magnitude of velocity will be the same at the points A and P because they are on the same level, but having opposite directions.

Therefore, the horizontal and vertical velocities at P will be ${v_x} =  - {v_0}\cos \theta $ and ${v_y} = {v_0}\sin \theta $ respectively.

Now, we have $h = ut + \dfrac{1}{2}a{t^2}$

Hence, $h =  - {v_0}\sin \theta \left( t \right) + \dfrac{1}{2}g{t^2}$

Also since the AT is $R + \Delta x = {v_0}\cos \theta  \cdot t$ ,that gives $t = \dfrac{{R + \Delta x}}{{{v_0}\cos \theta }}$

Now substituting this value in the above equation, we get

$ \Rightarrow h =  - {v_0}\sin \theta \left( {\dfrac{{R + \Delta x}}{{{v_0}\cos \theta }}} \right) + \dfrac{1}{2}g{\dfrac{{\left( {R + \Delta x} \right)}}{{{v_0}^2{{\cos }^2}\theta }}^2}$

That gives, since $\theta  = 45^\circ $

$ \Rightarrow h =  - \tan \theta \left( {R + \Delta x} \right) + \dfrac{1}{2}\left( {\dfrac{g}{{{v_0}^2}}} \right){\dfrac{{\left( {R + \Delta x} \right)}}{{\dfrac{1}{2}}}^2}$

$ \Rightarrow h =  - \left( {R + \Delta x} \right) + \left( {\dfrac{g}{{{v_0}^2}}} \right){\left( {R + \Delta x} \right)^2}$

Since, $\left( {\dfrac{g}{{{v_0}^2}}} \right) = \dfrac{1}{R}$ hence

$ \Rightarrow h =  - R - \Delta x + \dfrac{1}{R}\left( {{R^2} + \Delta {x^2} + 2R\Delta x} \right)$

i.e.

$ \Rightarrow h =  - R - \Delta x + R + \dfrac{{\Delta {x^2}}}{R} + 2\Delta x = \dfrac{{\Delta {x^2}}}{R} + \Delta x$

Hence,

$ \Rightarrow h = \Delta x\left[ {1 + \dfrac{{\Delta x}}{R}} \right]$

4.31. A particle is projected in air at an angle $\beta $ to a surface which itself is inclined at an angle $\alpha $ to the horizontal as in figure

(a) Find an expression of range on the plane surface (distance on the plane from the point of projection at which a particle will hit the surface.)

(Hint: This problem can be solved in two different ways:

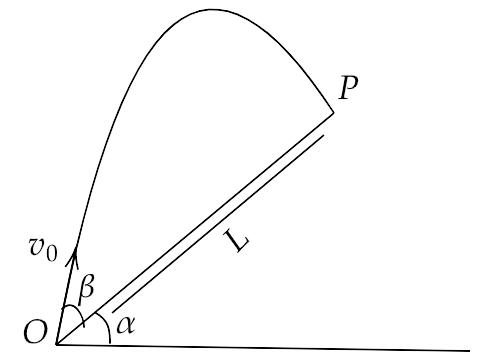
(i) Point P at which particle hits the plane can be seen as the intersection of its trajectory (parabola) and straight line. Remember a particle is projected at an angle $\left( {\alpha  + \beta } \right)$ w.r.t. horizontal.

(ii) We can take x-direction along the plane and y-direction perpendicular to the plane. In that case resolve g (acceleration due to gravity) in two different components, ${g_x}$ along the plane and ${g_y}$ perpendicular to the plane. Now the problem can be solved as two independent motions in x and y directions respectively with time as a common parameter.)

Ans: Now we find (a).

Since we have, $x = L,{u_x} = {v_0}\cos \beta ,{a_x} =  - g\sin \alpha $ and $t = T = \dfrac{{2{v_0}\sin \beta }}{{g\cos \alpha }}$

Hence, $s = {u_x}t + \dfrac{1}{2}{a_x}{t^2}$

Gives us, $L = {v_0}\cos \beta  \cdot T + \dfrac{1}{2}\left( { - g\sin \alpha } \right){T^2} = T\left[ {{v_0}\cos \beta  - \dfrac{1}{2}g\sin \alpha T} \right]$

Putting $T = \dfrac{{2{v_0}\sin \beta }}{{g\cos \alpha }}$ gives us,

$ \Rightarrow L = \dfrac{{2{v_0}^2\sin \beta }}{{g{{\cos }^2}\alpha }}\cos \left( {\alpha  + \beta } \right)$

That is the required range.

(b) Time of flight.

Ans: Let us first calculate the (b) time of flight.

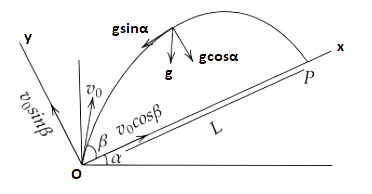
We have,

$ \Rightarrow s = ut + \dfrac{1}{2}g{t^2}$

Where, $s = 0,u = {u_y} = {v_0}\sin \beta ,g = {g_y} =  - g\cos \alpha ,t = T$

Hence,

$ \Rightarrow 0 = {v_0}\sin \beta \left( T \right) + \dfrac{1}{2}\left( { - g\cos \alpha } \right){T^2}$

i.e.

$ \Rightarrow T\left[ {{v_0}\sin \beta  - T\dfrac{g}{2}\cos \alpha } \right] = 0$

So either T is zero or ${v_0}\sin \beta  - T\dfrac{g}{2}\cos \alpha $

That gives the time of flight as $T = \dfrac{{2{v_0}\sin \beta }}{{g\cos \alpha }}$

(c) $\beta $ at Which range will be maximum.

Ans: Let us consider the equation $Z = \sin \beta \cos \left( {\alpha  + \beta } \right)$

We can write $Z = \sin \beta \cos \left( {\alpha  + \beta } \right) = \dfrac{1}{2}\left[ {\sin \left( {2\beta  + \alpha } \right) - \sin \alpha } \right]$

Now for Z to be maximum, it must have  $\sin \left( {2\beta  + \alpha } \right) = 1$ i.e. $\sin \left( {2\beta  + \alpha } \right) = \sin 90^\circ $

That gives, $2\beta  + \alpha  = 90^\circ $

Hence, $\beta  = \dfrac{{90^\circ  - \alpha }}{2}$ or $\beta  = \dfrac{\pi }{4} - \dfrac{\alpha }{2}$

4.32. A particle falling vertically from a height hits a plane surface inclined to horizontal at an angle with speed ${v_0}$ and rebounds elastically as shown in the figure. Find the distance along the plane where it will hit the second time.

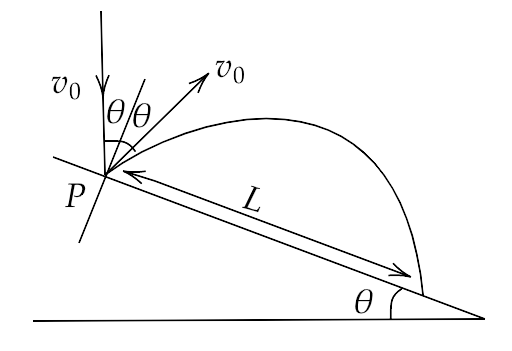
(Hint: (i) After rebound, the particle still has speed ${v_0}$ to start.

(ii) Work out angle particle speed is horizontal after it rebounds.

(iii) Rest is similar to if a particle is projected up the incline.)

Ans: Considering the motion of particle from the point O to the point A along y-axis, we can write

$ \Rightarrow {s_y} = {u_y}t + \dfrac{1}{2}{a_y}{t^2}$

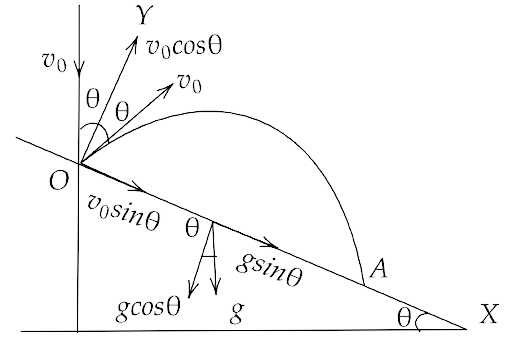
Where we have ${s_y} = 0,{u_y} = {v_0}\cos \theta ,t = T,{a_y} =  - g\cos \theta $

That gives us,

$ \Rightarrow 0 = {v_0}\cos \theta  \cdot T - \dfrac{1}{2}g\cos \theta {T^2}$

i.e.

$ \Rightarrow T\left[ {{v_0}\cos \theta  - \dfrac{1}{2}g\cos \theta T} \right] = 0$

Now since T can not be zero hence ${v_0}\cos \theta  = \dfrac{1}{2}g\cos \theta T$

That gives $\dfrac{{2{v_0}}}{g} = T$

Now, considering the motion along x-axis we have,

$ \Rightarrow {s_x} = {u_x}t + \dfrac{1}{2}{a_x}{t^2}$

That gives,

$ \Rightarrow L = \left( {\dfrac{{2{v_0}}}{g}} \right){v_0}\sin \theta  + \dfrac{1}{2}g\sin \theta {\left( {\dfrac{{2{v_0}}}{g}} \right)^2}$

$ \Rightarrow L = \dfrac{{2{v_0}^2\sin \theta }}{g} + \dfrac{{2{v_0}^2\sin \theta }}{g}$

$ \Rightarrow L = \dfrac{{4{v_0}^2}}{g}\sin \theta $

4.33. A girl riding a bicycle with a speed of 5 m/s towards the north direction, observes rain falling vertically down. If she increases her speed to 10 m/s, rain appears to meet her at 45° to the vertical. What is the speed of the rain? In what direction does rain fall as observed by a ground-based observer?

(Hint: Assume north to be $\widehat i$ direction and vertically downward to be $ - \widehat j$ . Let the rain velocity ${v_r}{\text{ be }}a\widehat i + b\widehat j$ . The velocity of rain as observed by the girl is always ${v_r} - {v_{girl}}$ . Draw the vector diagram/s for the information given and find a and b. You may draw all vectors in the reference frame of the ground-based observer.)

Ans: Let us consider the north direction as $\widehat i$ and the downward direction as $ - \widehat j$ respectively.

Consider the velocity of rain to be ${\overrightarrow v _R} = a\widehat i + b\widehat j$

Now if the speed of the girl is ${\overrightarrow v _g} = 5\widehat i$

Then the velocity of rain w.r.t. the girl will be ${\overrightarrow v _{Rg}} = \left( {a\widehat i + b\widehat j} \right) - 5\widehat i$

Now the direction of the rain is vertically downward, hence the horizontal component of ${\overrightarrow v _{Rg}}$ will be zero.

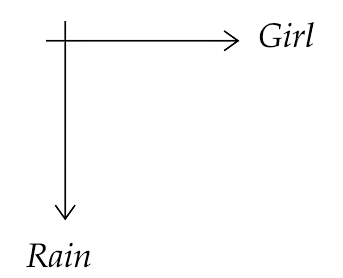
That gives us, $a\widehat i - 5\widehat i = 0$ or $a = 5$

Now if ${\overrightarrow v _g} = 10\widehat i$ and we have ${\overrightarrow v _R} = 5\widehat i + b\widehat j$

And ${\overrightarrow v _{Rg}} = \left( {5\widehat i + b\widehat j} \right) - 10\widehat i =  - 5\widehat i + b\widehat j$

Now rains appears at 45° to the vertical $\widehat j$ ,

Therefore, $\tan 45^\circ  = \dfrac{b}{a} \Rightarrow b = a$

Hence, $b =  - 5$

That gives ${\overrightarrow v _R} = 5\widehat i - 5\widehat j$

Now, $\left| {{{\overrightarrow v }_R}} \right| = \sqrt {{5^2} + {{\left( { - 5} \right)}^2}}  = \sqrt {50}  = 5\sqrt 2 m/s$

4.34. A river is flowing due east with a speed of 3m/s. A swimmer can swim in still water at a speed of 4 m/s as shown in the figure.

(a) If a swimmer starts swimming due north, what will be his resultant velocity (magnitude and direction)?

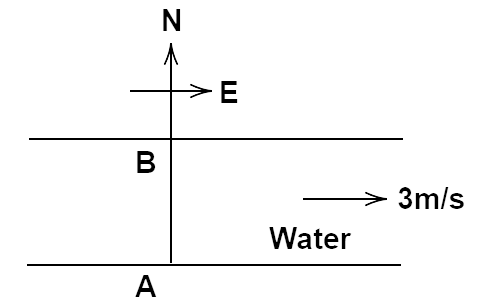
Ans: Given that, velocity towards AB and east are ${v_s} = 4m/s$ and ${v_R} = 3m/s$ respectively.

(a) Since the above given two velocities are perpendicular therefore,

We can write ${v^2} = v_s^2 + v_R^2 = 25 \Rightarrow v = 5m/s$

Also, $\tan \theta  = \dfrac{{{v_R}}}{{{v_s}}} = \dfrac{3}{4} = 0.75 \Rightarrow \theta  = {\tan ^{ - 1}}0.75 = 36^\circ 54'$

Hence $\theta $ is making $36^\circ 54$ with a north direction.

(b) If he wants to start from point A on the south bank and reaches the opposite point B on the north bank,

(i) which direction should he swim?

(ii) what will be his resultant speed?

Ans: If the swimmer strikes to swim with angle $\theta $ with north direction towards West,

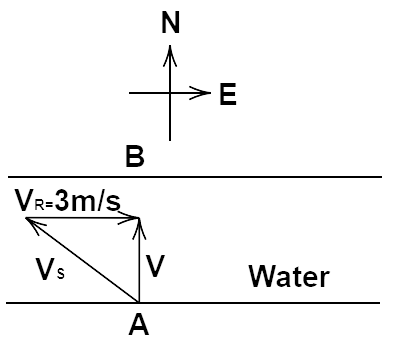
Then from figure we have, ${v^2} = v_s^2 - v_R^2 = 7 \Rightarrow v = \sqrt 7 m/s$

And 

Hence $\theta $ is made  between the north and west direction.

(c) From two different cases as mentioned in (a) and (b)above, in which case will he reach the opposite bank in a shorter time?

Ans: Here, the component of velocity perpendicular to the river is 4 m/s.

Let the width of the river be ${d_R}$.

Time taken by the swimmer when he strikes towards North will be ${t_1} = \dfrac{{{d_R}}}{4}$

Also, time taken in part (b) will be ${t_2} = \dfrac{{{d_R}}}{{\sqrt 7 }}$

Therefore, the ratio of both time taken is given by 

$ \Rightarrow \dfrac{{{t_1}}}{{{t_2}}} = \dfrac{{{d_R}}}{4} \times \dfrac{{\sqrt 7 }}{{{d_R}}} = \dfrac{{\sqrt 7 }}{4}$

That gives us the relation ${t_2} > {t_1}$.

Hence, the swimmer will reach the opposite bank in a shorter time in the case (a).

4.35. A cricket fielder can throw the cricket ball with a speed ${v_0}$ . If he throws the ball while running with speed u at an angle $\theta $ to the horizontal, find

(a) the effective angle to the horizontal at which the ball is projected in the air as seen by a spectator.

Ans: (a) Given that, a cricket fielder runs with velocity u in the horizontal direction and he throws the ball while running.

Therefore the horizontal component of the ball also includes his own speed u.

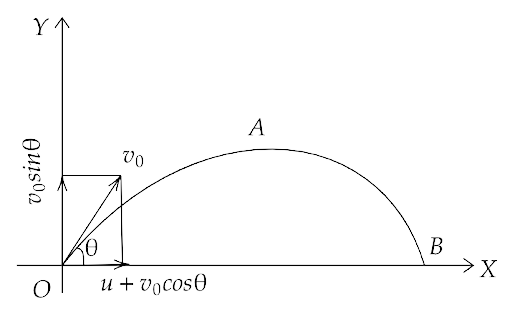
Hence, ${u_x} = u + {v_0}\cos \theta $

The fielder runs horizontally, hence the vertical component of velocity of the ball is not affected.

That gives, ${u_y} = {v_0}\sin \theta $

Also, we have $\tan \theta  = \dfrac{{{u_y}}}{{{u_x}}} = \dfrac{{{v_0}\sin \theta }}{{u + {v_0}\cos \theta }}$

Therefore, $\theta  = {\tan ^{ - 1}}\dfrac{{{v_0}\sin \theta }}{{u + {v_0}\cos \theta }}$

(b) what will be the time of flight?

Ans: Since we have, ${s_y} = {u_y}t + \dfrac{1}{2}{a_y}{t^2}$

Where ${s_y} = 0,{u_y} = {v_0}\sin \theta ,{a_y} =  - g,t = T$

Therefore, we get $0 = {v_0}\sin \theta \left( T \right) - \dfrac{1}{2}g{T^2}$

Or, $T\left[ {{v_0}\sin \theta  - \dfrac{1}{2}gT} \right] = 0$

Since T cannot be zero, therefore ${v_0}\sin \theta  = \dfrac{1}{2}gT$

That gives, $T = \dfrac{{2{v_0}\sin \theta }}{g}$

(c) what is the distance (horizontal range) from the point of projection at which the ball will land?

Ans: For the range to be maximum, we have $\dfrac{{dR}}{{d\theta }} = 0$

Therefore, $\dfrac{{d\dfrac{{{v_0}}}{g}\left[ {2u\sin \theta  + {v_0}\sin 2\theta } \right]}}{{d\theta }} = 0$

That gives, $\dfrac{{{v_0}}}{g}\left[ {2u\cos \theta  + 2{v_0}\cos \theta } \right] = 0$

(d) find θ at which he should throw the ball that would maximise the horizontal range as found in (c).

Ans: Now since $\dfrac{{{v_0}}}{g} \ne 0$ hence $2u\cos \theta  + 2{v_0}\cos \theta  = 0$

That gives, $2{v_0}{\cos ^2}\theta  + u\cos \theta  - {v_0} = 0$

Using quadratic formula we get, $\cos \theta  = \dfrac{{ - u \pm \sqrt {{u^2} + 8{v_0}^2} }}{{4{v_0}}}$

Hence, $\theta  = {\cos ^{ - 1}}\left( {\dfrac{{ - u \pm \sqrt {{u^2} + 8{v_0}^2} }}{{4{v_0}}}} \right)$

(e) how does θ for maximum range change if $u > {v_0},u = {v_0},u < {v_0}$

Ans: If we have $u = {v_0}$

Then $\cos \theta  = \dfrac{{ - {v_0} \pm \sqrt {{v_0}^2 + 8{v_0}^2} }}{{4{v_0}}} = \dfrac{{ - 1 \pm 3}}{2}$

Taking positive sign, $\cos \theta  = \dfrac{{ - 1 + 3}}{2} = \dfrac{1}{2}$

Hence, $\theta  = {\cos ^{ - 1}}\dfrac{1}{2} = 60^\circ $

Now, if $u <  < {v_0}$ then we have $\cos \theta  = \dfrac{{ - u \pm \sqrt {{u^2} + 8{v_0}^2} }}{{4{v_0}}} = \dfrac{{ - u \pm 2\sqrt 2 {v_0}}}{{4{v_0}}}$

Taking positive sign, $\cos \theta  = \dfrac{{2\sqrt 2 {v_0}}}{{4{v_0}}} = \dfrac{1}{{\sqrt 2 }}$

Hence, $\theta  = {\cos ^{ - 1}}\dfrac{1}{{\sqrt 2 }} = 45^\circ $

Also, if $u >  > {v_0}$ then we have $\cos \theta  = \dfrac{{ - u \pm \sqrt {{u^2} + 8{v_0}^2} }}{{4{v_0}}} = \dfrac{{ - u \pm u}}{{4{v_0}}}$

Taking positive sign, $\cos \theta  = \dfrac{{ - u + u}}{{4{v_0}}} = 0$

Hence, $\theta  = {\cos ^{ - 1}}0 = 90^\circ $

(f) how does θ in (v) compare with that for u = 0 (i.e. 45⁰)?

Ans: If we have $u = 0$

Then we have $\cos \theta  = \dfrac{{ - u \pm \sqrt {{u^2} + 8{v_0}^2} }}{{4{v_0}}} = \dfrac{{ \pm 2\sqrt 2 {v_0}}}{{4{v_0}}}$

Taking positive sign, $\cos \theta  = \dfrac{{2\sqrt 2 {v_0}}}{{4{v_0}}} = \dfrac{1}{{\sqrt 2 }}$

Hence, $\theta  = {\cos ^{ - 1}}\dfrac{1}{{\sqrt 2 }} = 45^\circ $

4.36. Motion in two dimensions in a plane can be studied by expressing position, velocity and acceleration as vectors in Cartesian co-ordinates $\overrightarrow A  = {A_x}\widehat i + {A_y}\widehat j$ where $\widehat i,\widehat j$ are unit vector along x and y directions, respectively and ${A_x}{\text{ and }}{A_y}$ are corresponding components of $\overrightarrow A $  (Figure). Motion can also be studied by expressing vectors in circular polar co-ordinates $\overrightarrow A  = {A_r}\widehat r + {A_\theta }\widehat \theta $ where $\widehat r = \dfrac{{\overrightarrow r }}{{\left| r \right|}} = \cos \theta \widehat i + \sin \theta \widehat j$ and $\widehat \theta  =  - \sin \theta \widehat i + \cos \theta \widehat j$ are unit vectors along direction in which ‘r’ and ‘θ ’ are increasing.

(a) Express $\widehat i$ and $\widehat j$ in terms of $\widehat r$ and $\widehat \theta $.

Ans: Given that, $\widehat r = \cos \theta \widehat i + \sin \theta \widehat j$ ...(1)

and $\widehat \theta  =  - \sin \theta \widehat i + \cos \theta \widehat j$  ...(2)

Multiplying them with $\sin \theta {\text{ and cos}}\theta $ respectively and adding

We get, $\widehat r\sin \theta  + \widehat \theta \cos \theta  = \widehat j$

Now, multiplying the first two equations with ${\text{cos}}\theta {\text{ and }}\sin \theta $ respectively and subtracting,

We get, $\widehat r\cos \theta  - \widehat \theta \sin \theta  = \widehat i$

These are the required relation of $\widehat i$ and $\widehat j$ in terms of $\widehat r$ and $\widehat \theta $.

(b) Show that both $\widehat r$ and $\widehat \theta $ are unit vectors and are perpendicular to each other.

Ans: Multiplying (1) and (2),

We get, $\widehat r \cdot \widehat \theta  = \left( {\cos \theta \widehat i + \sin \theta \widehat j} \right)\left( { - \sin \theta \widehat i + \cos \theta \widehat j} \right)$

Or, $\left| {\widehat r} \right| \cdot \left| {\widehat \theta } \right|\cos \theta  = 0$

Now since $\left| {\widehat r} \right|{\text{ and }}\left| {\widehat \theta } \right|$ can't be zero, therefore $\cos \theta  = 0 = \cos 90^\circ $

Therefore, the angle between $\widehat r$ and $\widehat \theta $ is $90^\circ $ .

(c) Show that $\dfrac{d}{{dt}}\widehat r = \omega \widehat \theta {\text{ where }}\omega  = \dfrac{{d\theta }}{{dt}}{\text{ and }}\dfrac{{d\widehat \theta }}{{dt}} =  - \omega \widehat r$

Ans: Since $\widehat r = \cos \theta \widehat i + \sin \theta \widehat j$

Therefore, $\dfrac{{d\widehat r}}{{dt}} = \dfrac{d}{{dt}}\left( {\cos \theta \widehat i + \sin \theta \widehat j} \right) =  - \sin \theta \dfrac{{d\theta }}{{dt}}\widehat i + \cos \theta \dfrac{{d\theta }}{{dt}}\widehat j$

Or, $\dfrac{{d\widehat r}}{{dt}} = \left( { - \sin \theta \widehat i + \cos \theta \widehat j} \right)\dfrac{{d\theta }}{{dt}} = \omega \left( { - \sin \theta \widehat i + \cos \theta \widehat j} \right) = \omega \widehat \theta $

Hence, $\dfrac{{d\widehat r}}{{dt}} = \omega \widehat \theta $

(d) For a particle moving along a spiral given by $\overrightarrow r  = \left| {\widehat a} \right|\left| {\widehat \theta } \right|\widehat r$ where a =1 (unit), find dimensions of ‘a’.

Ans: Given that $\overrightarrow r  = \left| {\widehat a} \right|\left| {\widehat \theta } \right|\widehat r$ 

Hence, their dimensions would be given by $\left[ {\widehat a} \right] = \dfrac{{\left[ {\overrightarrow r } \right]}}{{\left[ {\widehat \theta } \right]\left[ {\widehat r} \right]}}$

That gives us, $\left[ {\widehat a} \right] = \dfrac{{\left[ {{M^0}{L^1}{T^0}} \right]}}{{\left[ {{M^0}{L^0}{T^0}} \right]\left[ {{M^0}{L^0}{T^0}} \right]}} = \left[ {{M^0}{L^1}{T^0}} \right]$

Hence, $\left[ {\widehat a} \right] = \left[ {{M^0}{L^1}{T^0}} \right]$ , $\left[ {\widehat \theta } \right] = \left[ {{M^0}{L^0}{T^0}} \right]$ and $\left[ {\overrightarrow r } \right] = \left[ {{M^0}{L^0}{T^0}} \right]$

(e) Find velocity and acceleration in polar vector representation for particles moving along the spiral described in (d) above.

Ans: Given that $a = 1$ and $\overrightarrow r  = \widehat \theta \widehat r = \theta \left( {\cos \theta \widehat i + \sin \theta \widehat j} \right)$

Therefore, $v = \dfrac{{d\overrightarrow r }}{{dt}} = \dfrac{{d\theta }}{{dt}}\widehat r + \theta \dfrac{{d\widehat r}}{{dt}} = \dfrac{{d\theta }}{{dt}}\widehat r + \theta \dfrac{d}{{dt}}\left( {\cos \theta \widehat i + \sin \theta \widehat j} \right)$

$v = \dfrac{{d\theta }}{{dt}}\widehat r + \theta \left( { - \sin \theta \widehat i + \cos \theta \widehat j} \right)\dfrac{{d\theta }}{{dt}}$

Hence, $v = \omega \widehat r + \theta \widehat \theta \omega $

Now, $\overrightarrow a  = \dfrac{{dv}}{{dt}} = \dfrac{d}{{dt}}\left[ {\omega \widehat r + \theta \widehat \theta \omega } \right] = \dfrac{d}{{dt}}\left( {\dfrac{{d\theta }}{{dt}}\widehat r + \theta \widehat \theta \dfrac{{d\theta }}{{dt}}} \right)$

Solving above equation further,

Gives us, $\overrightarrow a  = \dfrac{{{d^2}\theta }}{{d{t^2}}}\widehat r + {\omega ^2}\widehat \theta  + \dfrac{{{d^2}\theta }}{{d{t^2}}}\left( {\theta \widehat \theta } \right) + {\omega ^2}\widehat \theta  + {\omega ^2}\left( { - \widehat r} \right)$

Hence, $\overrightarrow a  = \left( {\dfrac{{{d^2}\theta }}{{d{t^2}}} - {\omega ^2}\theta } \right)\widehat r + \left( {2{\omega ^2} + \dfrac{{{d^2}\theta }}{{d{t^2}}}\theta } \right)\widehat \theta $

4.37. A man wants to reach from A to the opposite corner of the square C (as in figure). The sides of the square are 100 m. A central square of 50m × 50m is filled with sand. Outside this square, he can walk at a speed of 1 m/s. In the central square, he can walk only at a speed of $v{\text{ }}m/s\left( {v < 1} \right)$ . What is the smallest value of v for which he can reach faster via a straight path through the sand than any path in the square outside the sand?

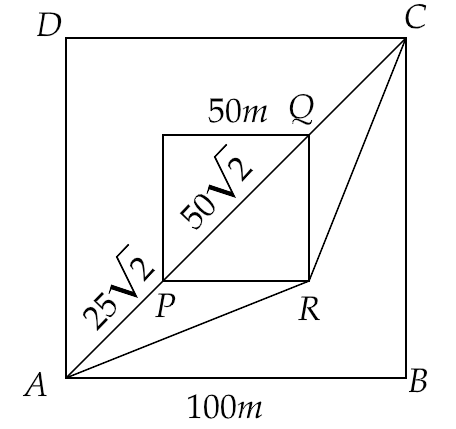
Ans: From the figure , we can obtain distance PQ by Pythagoras theorem,

Hence $PQ = \sqrt {{{50}^2} + {{50}^2}}  = 50\sqrt 2 $

Similarly, we have $AC = \sqrt {{{100}^2} + 10{0^2}}  = 100\sqrt 2 $

Total time taken in crossing the path APQC is given by,

$ \Rightarrow {t_1} = \dfrac{{\left( {AP + QC} \right)}}{{1m/s}} + \dfrac{{PQ}}{v}$

That is,

$ \Rightarrow {t_1} = \dfrac{{100\sqrt 2  - 50\sqrt 2 }}{1} + \dfrac{{50\sqrt 2 }}{v}$

$ \Rightarrow {t_1} = \dfrac{{50\sqrt 2 }}{1} + \dfrac{{50\sqrt 2 }}{v} = 50\sqrt 2 \left( {1 + \dfrac{1}{v}} \right)$

If O is the midpoint of PQ, then

Total time taken in crossing the path ARC is given by,

$ \Rightarrow {t_2} = \dfrac{{\left( {AR + RC} \right)}}{{1m/s}} = 2AR$

Now

$ \Rightarrow AR = \sqrt {{{\left( {50\sqrt 2 } \right)}^2} + {{\left( {25\sqrt 2 } \right)}^2}}  = \left( {25\sqrt 2 } \right)\sqrt 5  = 25\sqrt {10} s$

Hence,

$ \Rightarrow {t_2} = 2AR = 50\sqrt {10} s$

Now we have ${t_1} < {t_2}$

Hence, $50\sqrt 2 \left( {1 + \dfrac{1}{v}} \right) < 50\sqrt {10} $

$\left( {1 + \dfrac{1}{v}} \right) < \sqrt 5 $

That gives $\dfrac{1}{v} < \sqrt 5  - 1$

Hence, $v > \dfrac{1}{{\sqrt 5  - 1}} = \dfrac{{\sqrt 5  + 1}}{4} = \dfrac{{3.23}}{4} = 0.81$

Therefore, $v > 0.81s$.

Chapter Description

Motion in a plane is the fourth chapter of the NCERT class XI physics book part 1. After learning the concepts of motion of objects in a straight line, this chapter introduces us to the motion of objects in two directions, that is to say in a two-dimensional plane. The concept of vector and scalar values will be the first thing to be cleared in this chapter in section 4.2 ‘Scalars and Vectors.’. To make the exact measurement of the velocity and acceleration of a moving object we have to take the directions of movement into consideration. When we value physical quantities based on the directions with respect to a reference point then these are termed as vector quantities. 

It can't be wrong to say that vector quantities, except time, are the fundamental quantities involved in the expression of any other quantity. So this chapter has a very foundational character in the study of physics as a subject for quantification of laws of the natural world. In the sub-sections 4.2.1 ‘Position and Displacement Vectors,’ we will understand the nature of vectors. We will also get to know their arithmetic operations in 4.3 ‘Multiplication of Vectors by Real Numbers’ and 4.4 ‘Addition and Subtraction of Vectors’. Arithmetic operations have been established by both graphical and analytical methods. 

Various physical quantities mentioned in the previous chapter for example Velocity, acceleration, relative velocity have been explained with respect to a plane such as 'Motion in a plane with constant acceleration,' 'relative velocity in two dimensions,' etc. The most interesting of all is the 'Projectile motion' made by a moving object under the influence of gravity. All the variables of a horizontal projectile motion such as the range, maximum height obtained by the object, and time taken to achieve it have been clearly derived and established. Finally comes the concept of the ‘Uniform circular motion’ of an object. It is the motion of an object in a two-dimensional path by completing its circular  path of motion around a common point of reference called the ‘center.’

It is also important to bear in mind that the Exercises provided at the end of the chapter are as Important as the topic. so make sure that you complete all the questions provided in the chapter.  you can also refer to the solutions provided by vedantu.com. It has been prepared by very competent teachers and experts in their fields. You can get the solution in PDF format from this website.