NCERT Exemplar for Class 11 Maths Chapter 12 - Introduction to Three Dimensional Geometry (Book Solutions)

Solved Examples:

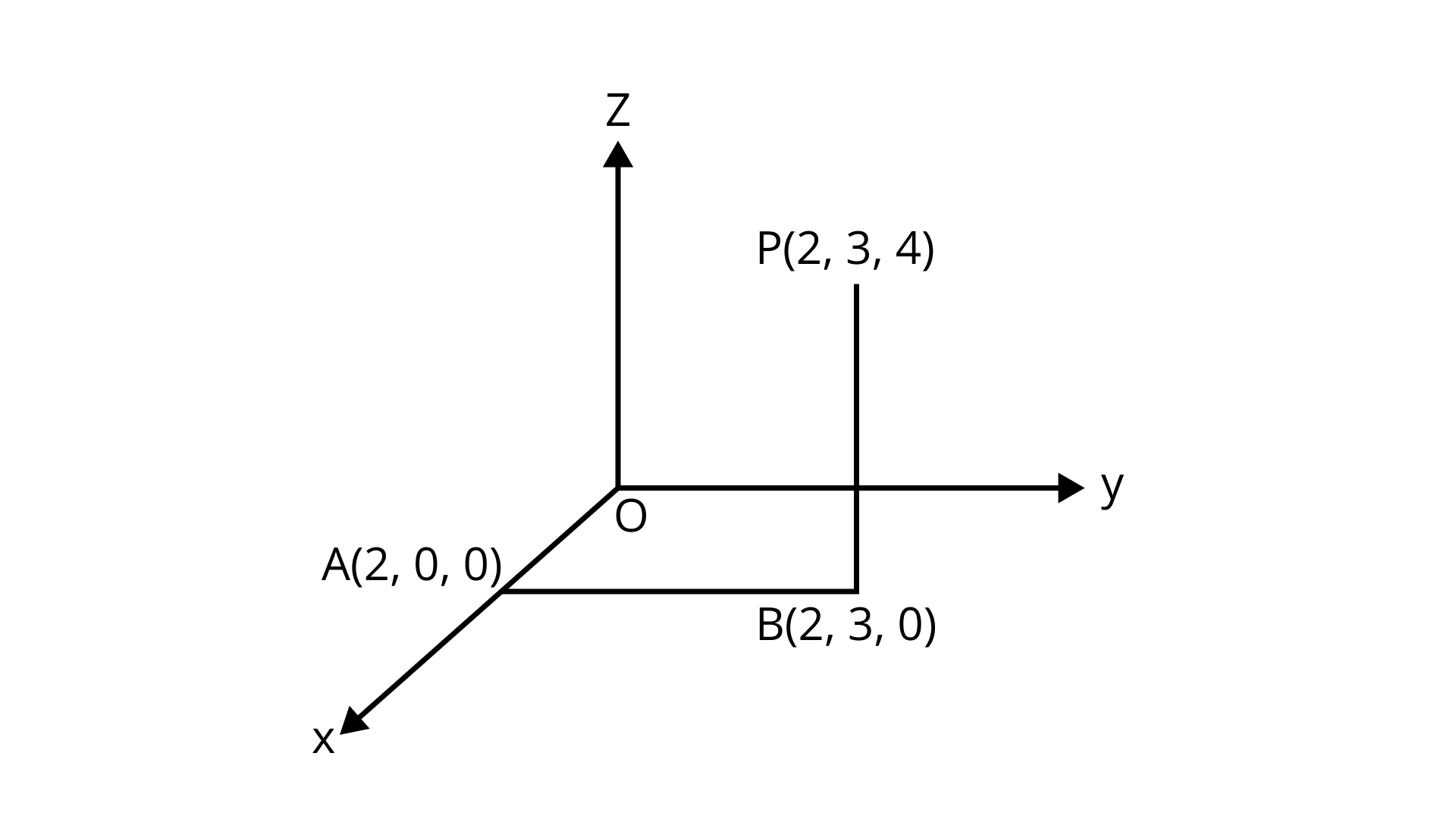
Sample Question 1:  Locate the points 

$\left( i \right) \left( {2, 3, 4} \right)$ in space.

Ans: To locate the point $\left( {2,{\text{ }}3,{\text{ }}4} \right)$ in space, we move $2$ units from O along the positive direction of x-axis. 

Let this point be A $\left( {2,{\text{ }}0,{\text{ }}0} \right)$.

From the point A move $3$ units parallel to +ve direction of y-axis. 

Let this point be B $\left( {2,{\text{ }}3,{\text{ }}0} \right)$.

From point B move $4$ units along the positive direction of the z-axis. 

Let this point be P $\left( {2,{\text{ }}3,{\text{ }}4} \right)$.

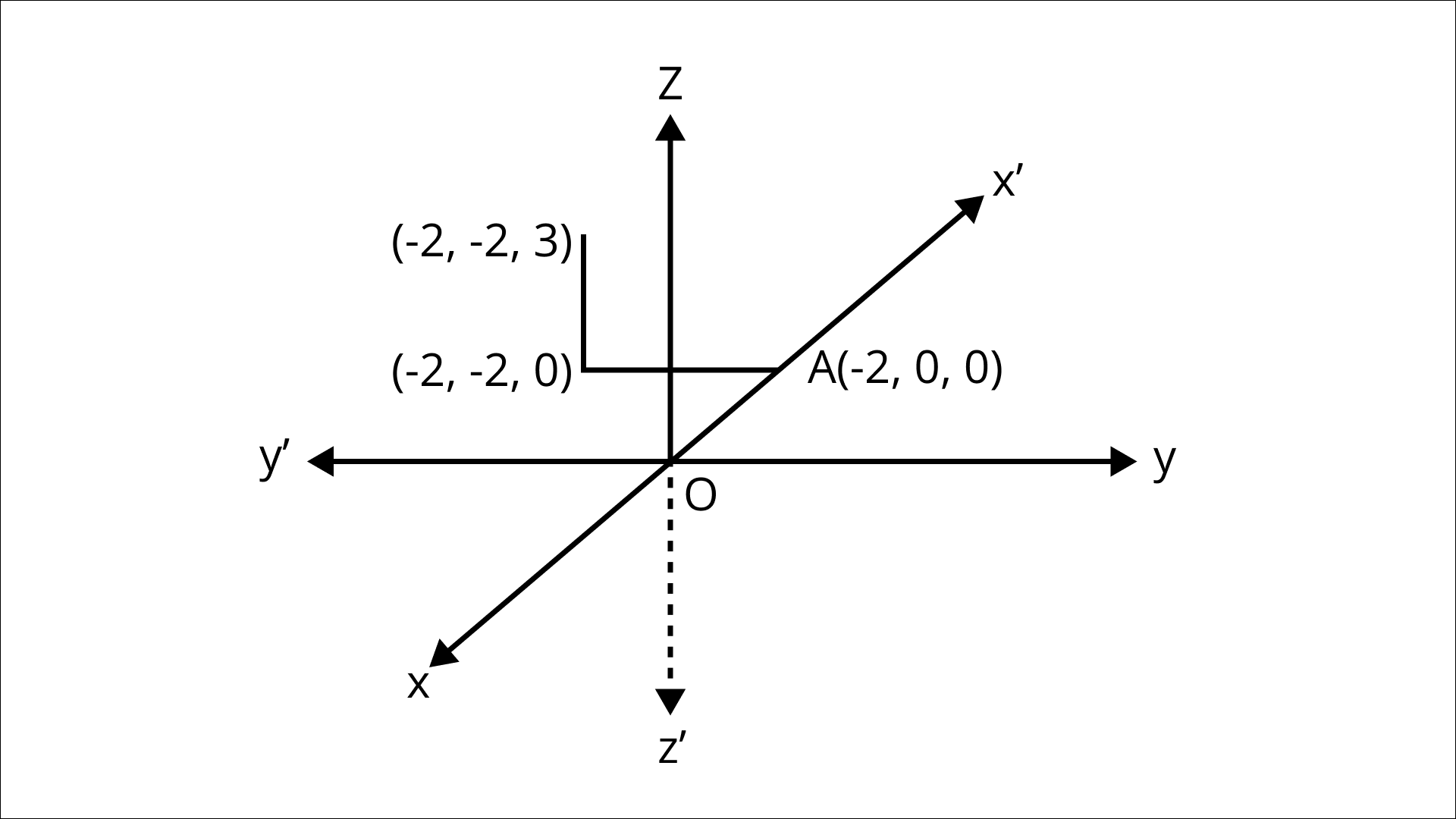
$\left( {ii} \right) \left( {-2, -2, 3} \right)$ in space.

Ans: From the origin, move $2$ units along the negative direction of the x-axis. Let this point be A $\left( {-2,{\text{ }}0,{\text{ }}0} \right)$. From the point A moves $2$ units parallel to the negative direction of the y-axis. Let this point be B$\left( {-2,{\text{ }}-2,{\text{ }}0} \right)$. From B move$3$units parallel to the positive direction of the z - axis. This is our required point Q $\left( {-2,{\text{ }}-2,{\text{ }}3} \right)$.

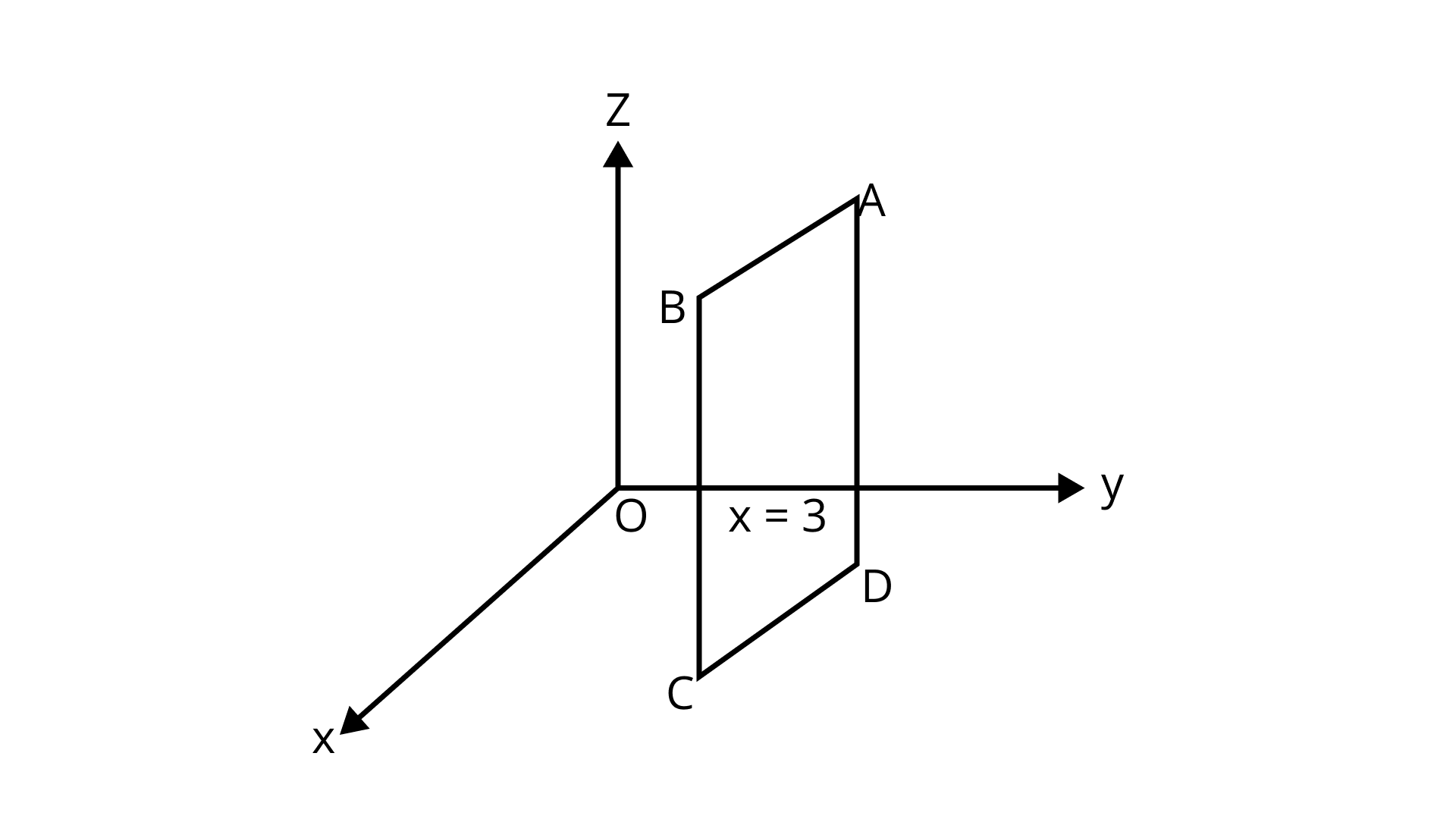
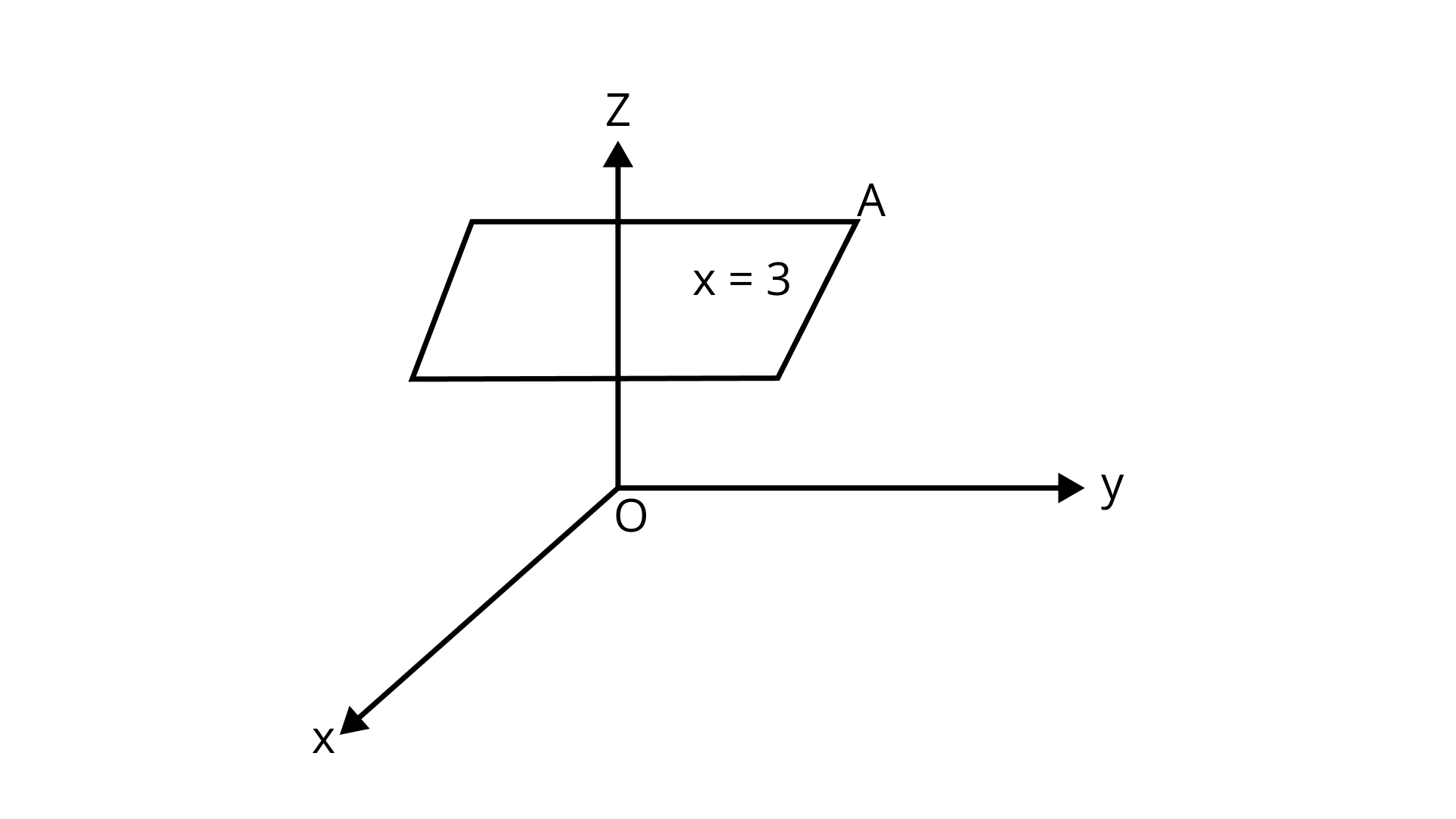
Sample Question 2:  Sketch the plane 

$\left( i \right) x  =  1$

Ans:

$x = 1$ is the plane at a distance of  $1$ unit from yz - plane.

$\left( {ii} \right) y  =  3$

Ans: 

$y = 3$ is the plane at a distance of  $3$ unit from xz - plane. 

$\left( {iii} \right) z  =  4$

Ans:

$z = 3$ is the plane at a distance of  $3$ unit from the xy - plane. 

Sample Question 3: Let L, M, N be the feet of the perpendiculars drawn from a point $P \left( {3, 4, 5} \right)$ on the x, y and z-axes respectively. Find the coordinates of L, M and N.

Ans: Since L is the foot of perpendicular from P on the x-axis, its y and z coordinates are zero. The coordinates of L are $(3,0,0)$. M is the foot of perpendicular from P on the y-axis, its x and z coordinates are zero.  The coordinates of M are$(0,4,0)$. N is the foot of perpendicular from P on the z-axis, its x and y coordinates are zero. The coordinates of M are $(0,0,5)$.

Sample Question 4: Let L, M, N be the feet of the perpendicular segments drawn from a point P (3, 4, 5) on the xy, yz and zx-planes, respectively. What are the coordinates of L, M and N?

Ans: Since L is the foot of the perpendicular segment from P on the xy-plane, the z-coordinate is zero in the xy-plane. Hence, coordinates of L are$(3,4,0)$.

M is the foot of the perpendicular segment from P on the yz-plane, x-coordinate is zero in the yz-plane. Hence, coordinates of M are $(0,4,5)$. 

N is the foot of the perpendicular segment from P on the xz-plane, y-coordinate is zero in the xz-plane. Hence, coordinates of N are $(3,0,5)$.  

Sample Question 5:  Let L, M, N are the feet of the perpendiculars drawn from the point $P \left( {3, 4, 5} \right)$ on the xy, yz and zx-planes, respectively. Find the distance of these points L, M, N from the point P, Fig.12.7.

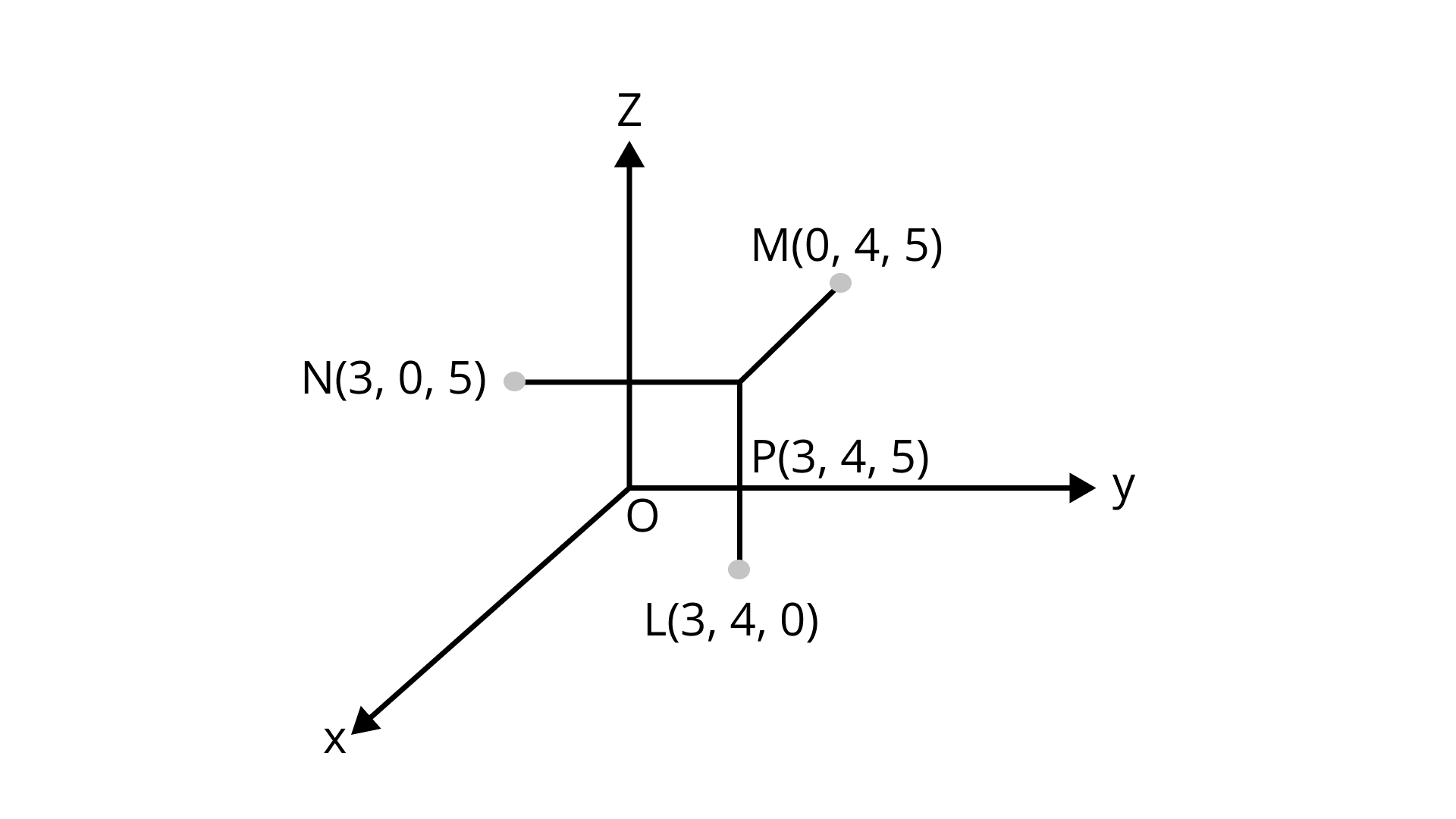
Ans: Since L is the foot of the perpendicular segment from P on the xy-plane, the z-coordinate is zero in the xy-plane. So, coordinates of L are$(3,4,0)$.

Thus , the distance between P and L is $5$ units.

M is the foot of the perpendicular segment from P on the yz-plane, x-coordinate is zero in the yz-plane. So, coordinates of M are $(0,4,5)$. 

Thus , the distance between P and M is $3$ units.

N is the foot of the perpendicular segment from P on the xz-plane, y-coordinate is zero in the xz-plane. So, coordinates of N are $(3,0,5)$.  

Thus , the distance between P and N is $4$ units.

Sample Question 6:  Using distance formula, show that the points ${\text{P }}\left( {{\text{2, 4, 6}}} \right){\text{, Q }}\left( {{\text{- 2, - 2, - 2}}} \right){\text{ and R }}\left( {{\text{6, 10, 14}}} \right)$ are collinear.

Ans: Given:  Coordinates of three points ${\text{P }}\left( {{\text{2, 4, 6}}} \right){\text{, Q }}\left( {{\text{- 2, - 2, - 2}}} \right){\text{ and R }}\left( {{\text{6, 10, 14}}} \right)$

Three points are collinear if the sum of any two distances is equal to the third distance.

So , show ${\text{QR  =  PQ  +  PR}}$

$\Rightarrow PQ = \sqrt {{{\left( {2 - ( - 2)} \right)}^2} + {{\left( {4 - ( - 2)} \right)}^2} + {{\left( {6 - ( - 2)} \right)}^2}}$

$\Rightarrow PQ = \sqrt {{{\left( 4 \right)}^2} + {{\left( 6 \right)}^2} + {{\left( 8 \right)}^2}}  = \sqrt {16 + 36 + 64}  = \sqrt {116} \, = 2\sqrt {29}$

$\Rightarrow Q R=\sqrt{(6-(-2))^{2}+(10-(-2))^{2}+(14-(-2))^{2}}$

$\Rightarrow Q R=\sqrt{(8)^{2}+(12)^{2}+(16)^{2}}=\sqrt{64+144+256}=\sqrt{464}=4 \sqrt{29}$

$\Rightarrow P R=\sqrt{(2-6)^{2}+(4-10)^{2}+(6-14)^{2}}$

$\Rightarrow P R=\sqrt{(-4)^{2}+(-6)^{2}+(-8)^{2}}=\sqrt{16+36+64}=\sqrt{116}=2 \sqrt{29}$

$\Rightarrow \mathrm{PQ}+\mathrm{PR}=2 \sqrt{29}+2 \sqrt{29}=4 \sqrt{29}=Q R$

Hence, proved.

Sample Question 7:  Find the coordinates of a point equidistant from the four points 

$O \left( {0, 0, 0} \right), A \left( {l, 0, 0} \right), B \left( {0, m, 0} \right) \,and C \left( {0, 0, n} \right).$

An: Given: coordinates of four points ${\text{O }}\left( {{\text{0, 0, 0}}} \right){\text{, A }}\left( {{\text{l, 0, 0}}} \right){\text{, B }}\left( {{\text{0, m, 0}}} \right){\text{ and C }}\left( {{\text{0, 0, n}}} \right)$

Let the required point be  ${\text{P(}}{\text{x}}{\text{,}}{\text{y}}{\text{,}}{\text{z}}{\text{)}}$

$\Rightarrow {\text{PO}}{\text{ = }}{\text{PB}}{\text{ = }}{\text{PC}}{\text{ = }}{\text{PD}}$

$\Rightarrow PO = PA$

$\Rightarrow \sqrt {{{\left( {x - 0} \right)}^2} + {{\left( {y - 0} \right)}^2} + {{\left( {z - 0} \right)}^2}}  = \sqrt {{{\left( {x - l} \right)}^2} + {{\left( {y - 0} \right)}^2} + {{\left( {z - 0} \right)}^2}}$

$\Rightarrow \sqrt {{x^2} + {y^2} + {z^2}}  = \sqrt {{x^2} + {l^2} - 2xl + {y^2} + {z^2}}$

$\Rightarrow {x^2} + {y^2} + {z^2} = {x^2} + {l^2} - 2xl + {y^2} + {z^2}$

$\Rightarrow {l^2} = 2xl$

$\Rightarrow x = \dfrac{l}{2}$

$\Rightarrow PO = PB$

$\Rightarrow \sqrt {{{\left( {x - 0} \right)}^2} + {{\left( {y - 0} \right)}^2} + {{\left( {z - 0} \right)}^2}}  = \sqrt {{{\left( {x - 0} \right)}^2} + {{\left( {y - m} \right)}^2} + {{\left( {z - 0} \right)}^2}}$

$\Rightarrow \sqrt {{x^2} + {y^2} + {z^2}}  = \sqrt {{x^2} + {m^2} - 2ym + {y^2} + {z^2}}$

$\Rightarrow {x^2} + {y^2} + {z^2} = {x^2} + {m^2} - 2ym + {y^2} + {z^2}$

$\Rightarrow {m^2} = 2ym$

$\Rightarrow y = \dfrac{m}{2}$

$\Rightarrow PO = PB$

$\Rightarrow \sqrt {{{\left( {x - 0} \right)}^2} + {{\left( {y - 0} \right)}^2} + {{\left( {z - 0} \right)}^2}}  = \sqrt {{{\left( {x - 0} \right)}^2} + {{\left( {y - 0} \right)}^2} + {{\left( {z - n} \right)}^2}}$

$\Rightarrow \sqrt {{x^2} + {y^2} + {z^2}}  = \sqrt {{x^2} + {n^2} - 2zn + {y^2} + {z^2}}$

$\Rightarrow {x^2} + {y^2} + {z^2} = {x^2} + {n^2} - 2zn + {y^2} + {z^2}$

$\Rightarrow {n^2} = 2zn$

$\Rightarrow z = \dfrac{n}{2}$

So, required point is $\left( {\dfrac{l}{2},\dfrac{m}{2},\dfrac{n}{2}} \right)$

Sample Question 8:  Find the point on x-axis which is equidistant from the point $A{\text{ }}\left( {3,{\text{ }}2,{\text{ }}2} \right){\text{ and }}B{\text{ }}\left( {5,{\text{ }}5,{\text{ }}4} \right)$.

Ans: Given:  Coordinates of two points $A{\text{ }}\left( {3,{\text{ }}2,{\text{ }}2} \right){\text{ and }}B{\text{ }}\left( {5,{\text{ }}5,{\text{ }}4} \right)$

Point on the x-axis is of form $C\left( {x,{\text{ 0}},{\text{ 0}}} \right)$

$AC = BC$

$\Rightarrow \sqrt {{{\left( {3 - x} \right)}^2} + {{\left( {2 - 0} \right)}^2} + {{\left( {2 - 0} \right)}^2}}  = \sqrt {{{\left( {5 - x} \right)}^2} + {{\left( {5 - 0} \right)}^2} + {{\left( {4 - 0} \right)}^2}}$

$\Rightarrow \sqrt {9 + {x^2} - 6x + 4 + 4}  = \sqrt {25 + {x^2} - 10x + 25 + 16}$

$\Rightarrow \sqrt {17 + {x^2} - 6x}  = \sqrt {66 + {x^2} - 10x}$

$\Rightarrow 17 + {x^2} - 6x = 66 + {x^2} - 10x$

$\Rightarrow 17 - 6x = 66 - 10x$

$\Rightarrow 4x = 45$

$\Rightarrow x = \dfrac{{45}}{4}$

So, Required point is $\left( {\dfrac{{49}}{4},{\text{ 0}},{\text{ 0}}} \right)$

Sample Question 9:  Find the point on y-axis which is at a distance $\sqrt {10}$  from the point $\left( {1,{\text{ }}2,{\text{ }}3} \right)$.

Ans: Given:  coordinates of a point Let us say ${\text{A}}\left( {1,{\text{ }}2,{\text{ }}3} \right)$

Point on the y-axis is of form $B\left( {0, y, 0} \right)$

$AB = \sqrt {10}$

$\Rightarrow \sqrt {{{\left( {0 - 1} \right)}^2} + {{\left( {y - 2} \right)}^2} + {{\left( {0 - 3} \right)}^2}}  = \sqrt {10}$

$\Rightarrow \sqrt {1 + {y^2} - 2y +  + 1 + 9}  = \sqrt {10}$

$\Rightarrow \sqrt {11 + {y^2} - 2y}  = \sqrt {10}$

$\Rightarrow 11 + {y^2} - 2y = 10$

$\Rightarrow {y^2} - 2y + 1 = 0$

$\Rightarrow {\left( {y - 2} \right)^{^2}} = 0$

$\Rightarrow y - 2 = 0$

$\Rightarrow y = 2$

So, required point is $\left( {0,{\text{ }}2,{\text{ 0}}} \right)$

Sample Question 10:  If a parallelepiped is formed by planes drawn through the points $\left( {{\text{2, 3, 5}}} \right){\text{ and }}\left( {{\text{5, 9, 7}}} \right)$ parallel to the coordinate planes, then find the length of edges of a parallelepiped and length of the diagonal.

Ans: Given:   Parallelepiped formed by planes drawn through the points $\left( {{\text{2, 3, 5}}} \right){\text{ and }}\left( {{\text{5, 9, 7}}} \right)$ parallel to the coordinate planes

Length of edges of a parallelepiped are  $|2 - 5|,|3 - 9|,|5 - 7|$ =  $3,6,2$

Length of the diagonal  =$\sqrt {{{\left( {2 - 5} \right)}^2} + {{\left( {3 - 9} \right)}^2} + {{\left( {5 - 7} \right)}^2}} |$

Length of the diagonal  = $\sqrt {{{\left( { - 3} \right)}^2} + {{\left( { - 6} \right)}^2} + {{\left( { - 2} \right)}^2}} | = \sqrt {9 + 36 + 4}  = \sqrt {49}  = 7$

So, Length of edges of a parallelepiped are $3,6,2$ and length of the diagonal is $7$ units.

Sample Question 11:  Show that the points $\left( {0, 7, 10} \right)\left( {-1, 6, 6} \right) \left( {- 4, 9, 6} \right),$ form a right angled isosceles triangle.

Ans: Given: Coordinates of three points.

Let these be $A\left( {0,{\text{ }}7,{\text{ }}10} \right),{\text{ B}}\left( {-1,{\text{ }}6,{\text{ }}6} \right){\text{ and C}}\left( {-{\text{ }}4,{\text{ }}9,{\text{ }}6} \right)$

$\Rightarrow AB = \sqrt {{{\left( {0 - ( - 1)} \right)}^2} + {{\left( {7 - 6} \right)}^2} + {{\left( {10 - 6} \right)}^2}}$

$\Rightarrow AB = \sqrt {{{\left( 1 \right)}^2} + {{\left( 1 \right)}^2} + {{\left( 4 \right)}^2}}  = \sqrt {1 + 1 + 16}  = \sqrt {18}  = 3\sqrt 2$

$\Rightarrow BC = \sqrt {{{\left( { - 1 - ( - 4)} \right)}^2} + {{\left( {6 - 9} \right)}^2} + {{\left( {6 - 6} \right)}^2}}$

$\Rightarrow BC = \sqrt {{{\left( 3 \right)}^2} + {{\left( { - 3} \right)}^2} + {{\left( 0 \right)}^2}}  = \sqrt {9 + 9}  = \sqrt {18}  = 3\sqrt 2$

$\Rightarrow CA = \sqrt {{{\left( { - 4 - 0} \right)}^2} + {{\left( {9 - 7} \right)}^2} + {{\left( {6 - 10} \right)}^2}}$

$\Rightarrow CD = \sqrt {{{\left( { - 4} \right)}^2} + {{\left( 2 \right)}^2} + {{\left( { - 4} \right)}^2}}  = \sqrt {16 + 4 + 16}  = \sqrt {36}  = 6$

$\therefore AB = BC = 3\sqrt 2$ so, ABC is an isosceles triangle

Also, $A{B^2} + B{C^2} = \left( {3\sqrt 2 } \right) + \left( {3\sqrt 2 } \right) = 18 + 18 = 36 = A{C^2}$

So, ABC is a right  triangle by Pythagoras theorem.

Hence, given points form a right angled isosceles triangle.

Sample Question 12:  Show that the points $\left( {5,{\text{ }}-1,{\text{ }}1} \right),\left( {7,{\text{ }}-{\text{ }}4,{\text{ }}7} \right),\left( {1{\text{ }}-{\text{ }}6,{\text{ }}10} \right){\text{and}}\left( {-1,{\text{ }}-{\text{ }}3,{\text{ }}4} \right)$ are the vertices of a rhombus.

Ans: Given:  Coordinates of four points.

Let these be $A\left( {5,{\text{ }}-1,{\text{ }}1} \right),B\left( {7,{\text{ }}-{\text{ }}4,{\text{ }}7} \right),C\left( {1{\text{ }}-{\text{ }}6,{\text{ }}10} \right){\text{and}}D\left( {-1,{\text{ }}-{\text{ }}3,{\text{ }}4} \right)$

$\Rightarrow AB = \sqrt {{{\left( {5 - 7} \right)}^2} + {{\left( { - 1 - ( - 4)} \right)}^2} + {{\left( {1 - 7} \right)}^2}}$

$\Rightarrow AB = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( 3 \right)}^2} + {{\left( { - 6} \right)}^2}}  = \sqrt {4 + 9 + 36}  = \sqrt {49}  = 7$

$\Rightarrow BC = \sqrt {{{\left( {7 - 1} \right)}^2} + {{\left( { - 4 - ( - 6)} \right)}^2} + {{\left( {7 - 10} \right)}^2}}$

$\Rightarrow BC = \sqrt {{{\left( 6 \right)}^2} + {{\left( 2 \right)}^2} + {{\left( { - 3} \right)}^2}}  = \sqrt {36 + 4 + 9}  = \sqrt {49}  = 7$

$\Rightarrow CD = \sqrt {{{\left( {1 - ( - 1)} \right)}^2} + {{\left( { - 6 - ( - 3)} \right)}^2} + {{\left( {10 - 4} \right)}^2}}$

$\Rightarrow CD = \sqrt {{{\left( 2 \right)}^2} + {{\left( { - 3} \right)}^2} + {{\left( 6 \right)}^2}}  = \sqrt {4 + 9 + 36}  = \sqrt {49}  = 7$

$\Rightarrow DA = \sqrt {{{\left( { - 1 - 5} \right)}^2} + {{\left( { - 3 - ( - 1)} \right)}^2} + {{\left( {4 - 1} \right)}^2}}$

$\Rightarrow DA = \sqrt {{{\left( { - 6} \right)}^2} + {{\left( { - 2} \right)}^2} + {{\left( 3 \right)}^2}}  = \sqrt {36 + 4 + 9}  = \sqrt {49}  = 7$

So, ${\text{AB  =  BC  =  CD  =  DA}}$

Hence, A , B , C and D are the vertices of Rhombus.

Sample Question 13: Find the ratio in which the line segment joining the points $(2,4,5) and (3, 5,  -  4)$ is divided by the $xz -$ plane.

Ans: Given: Points $(2,4,5){\text{ and (3, 5, }} - {\text{ 4)}}.$

Here,

Coordinates of point ${\text{C(x, y, z)}}$ will be ${\text{x  =  }}\dfrac{{3{\text{k  +  2}}}}{{{\text{k  +  1}}}},{\text{ y  =  }}\dfrac{{5{\text{k  +  4}}}}{{{\text{k  +  1}}}},{\text{ z  =  }}\dfrac{{ - {\text{ 4k  +  5}}}}{{{\text{k  +  1}}}}.$

As, the point lies in ${\text{xz - }}$ plane. The ${\text{y  - }}$ coordinate must be zero.

$\therefore {\text{ }}\dfrac{{{\text{5k  +  4}}}}{{{\text{k  +  1}}}}{\text{  =  0}}$

$\Rightarrow {\text{ k  =  }} - {\text{ }}\dfrac{4}{5}$ 

Negative sign indicates the external ratio $4{\text{ : 5}}{\text{.}}$

Sample Question 14: Find the coordinate of the point P which is five - sixth of the way from ${\text{A}}( - 2,0,6){\text{ and B(10, }} - 6{\text{, }} - {\text{ 12)}}{\text{.}}$

Ans: Given: Point ${\text{P}}$ is five - sixth of the way from ${\text{A}}( - 2,0,6){\text{ and B(10, }} - 6{\text{, }} - {\text{ 12)}}{\text{.}}$

As, point ${\text{P}}$ divides ${\text{AB}}$ in ratio $5{\text{ : 1}}{\text{.}}$

$\therefore {\text{ P(x, y, z)  =  }}\left( {\dfrac{{5{\text{ }} \times {\text{ 10  +  1 }} \times {\text{ }} - \,{\text{2}}}}{{5{\text{  +  1}}}},{\text{ }}\dfrac{{5{\text{ }} \times {\text{ }} - {\text{ 6  +  1 }} \times {\text{ 0}}}}{{5{\text{  +  1}}}},{\text{ }}\dfrac{{5{\text{ }} \times {\text{ }} - {\text{ 12  +  1 }} \times {\text{ 6}}}}{{5{\text{  +  1}}}}} \right)$

$\Rightarrow {\text{ P(x, y, z)  =  (8, }} - {\text{ 5, }} - {\text{ 9)}}$ 

Sample Question 15: Describe the vertices and edges of the rectangular parallelepiped with vertex $(3,{\text{ 5, 6)}}$ placed in the first octant with one vertex at origin and edges of parallelepiped lie along ${\text{x, y and z - }}$ axes.

Ans: Given: Rectangular parallelepiped with vertex $(3,{\text{ 5, 6)}}$ in first octant and edges along ${\text{x, y and z - }}$ axes.

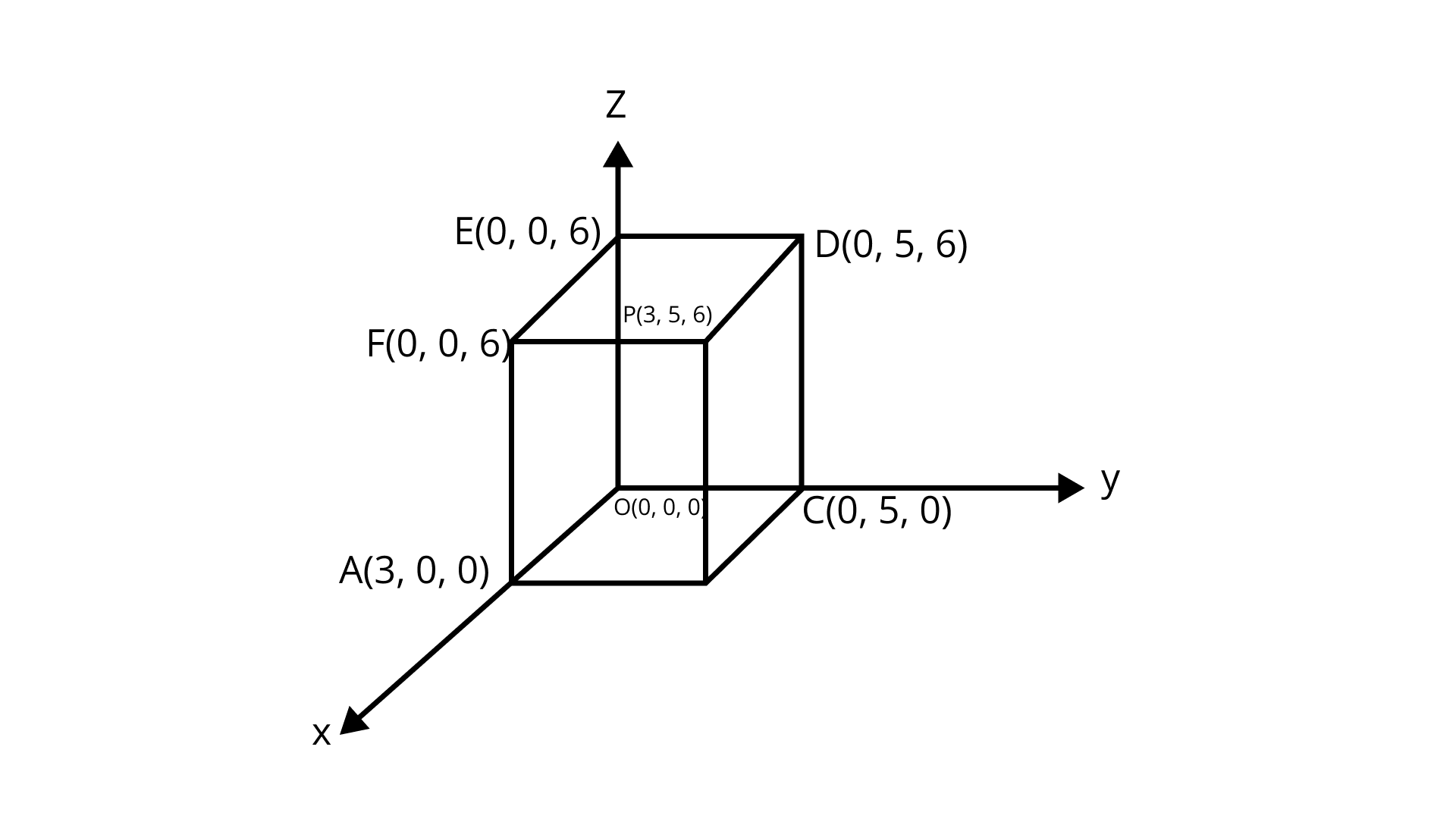
The coordinates of points ${\text{C}}(0,{\text{ 5, 0), A(3, 0, 0) \,and\, E(0, 0, 6)}}$ are on ${\text{y, x and z}}$ axes respectively. The foot of perpendicular from point will be ${\text{C}}(3,{\text{ 0, 6), D(0, 5, 6) and F(3, 0, 6)}}{\text{.}}$

Plane ${\text{OABC}}$ lies in the ${\text{xy  - }}$ plane. The ${\text{z  - }}$ coordinate of every point in this plane is zero. ${\text{z  =  0}}$ is the equation of this ${\text{xy  - }}$ plane. Plane ${\text{PDEF}}$ is parallel to ${\text{xy  - }}$ plane and $6$ unit distance above it. The equation of the plane is ${\text{z  =  6}}.$ Plane ${\text{ABPF}}$ represents plane ${\text{x  =  3}}$. Plane ${\text{OCDE}}$ lies in the yz-plane and ${\text{x  =  0}}$ is the equation of this plane. Plane ${\text{AOEF}}$ lies in the ${\text{xz  - }}$ plane. The y coordinate of every point in this plane is zero. Therefore, ${\text{y  =  0}}$ is the equation of plane. Plane ${\text{BDCP}}$ is parallel to the plane ${\text{AOEF}}$ at a distance ${\text{y  =  5}}.$ Edge ${\text{OA}}$ lies on the ${\text{x  - }}$ axis. The ${\text{x  - }}$ axis has equation ${\text{y  =  0 and z  =  0}}{\text{.}}$ For edges, we can use the equation of line through two points.

Here, 

${\text{DP, }}\dfrac{{{\text{x }} - {\text{ 0}}}}{{3 - {\text{ 0}}}}{\text{  =  }}\dfrac{{{\text{y }} - {\text{ 5}}}}{{5{\text{ }} - {\text{ 5}}}}\, = \dfrac{{{\text{z }} - {\text{ 6}}}}{{6 - \,{\text{6}}}}{\text{  =  k}}$

$\Rightarrow {\text{x  =  3k}}$ 

Using these edges can be described.

Sample Question 16: Let $A(3, 2, 0), B(5, 3, 2) and \,C( -  9, 6,  -  3)$ be three points forming a triangle. $AD$ the bisector of  Find the coordinates of point ${\text{D}}{\text{.}}$

Ans: Given: ${\text{A}}(3,{\text{ 2, 0), B(5, 3, 2) and C(}} - {\text{ 9, 6, }} - {\text{ 3)}}$ be three points of triangle.

${\text{AB  =  }}\sqrt {{{(5{\text{ }} - {\text{ 3}})}^2}{\text{  +  (3 }} - {\text{ 2}}{)^2}{\text{  +  (2 }} - {\text{ 0}}{)^2}}$

$= {\text{ }}\sqrt {4{\text{  +  1  +  4}}}$

$= {\text{ 3}}$

${\text{BC  = }}\sqrt {{{( - 9{\text{ }} - {\text{ 5}})}^2}{\text{  +  (6 }} - {\text{ 3}}{)^2}{\text{  +  (}} - 3{\text{ }} - {\text{ 2}}{)^2}}$

$= {\text{ }}\sqrt {144{\text{  +  16  +  9}}}$

$= 13$

${\text{As, AD is the bisector of }}\angle {\text{BAC,}}$

$\Rightarrow {\text{ }}\dfrac{{{\text{BD}}}}{{{\text{DC}}}}{\text{  =  }}\dfrac{{{\text{AB}}}}{{{\text{AC}}}}{\text{  =  }}\dfrac{3}{{13}}$

$\Rightarrow {\text{ D divides BC in the ratio 3 : 13}}$

$\therefore {\text{ Coordinates of D are,}}$

$= {\text{ }}\left( {\dfrac{{3( - {\text{ 9)  +  13(5)}}}}{{3{\text{  +  13}}}},{\text{ }}\dfrac{{3(6){\text{  +  13(3)}}}}{{3{\text{  +  13}}}},\dfrac{{3( - {\text{ 3)  +  13(2)}}}}{{3{\text{  +  13}}}}} \right)$

$= {\text{ }}\left( {\dfrac{{19}}{8},{\text{ }}\dfrac{{57}}{{16}},{\text{ }}\dfrac{{17}}{{16}}} \right)$ 

Sample Question 17: Determine the point in yz - plane which is equidistant from three points ${\text{A}}(2,{\text{ 0, 3), B(0, 3, 2) and C(0, 0, 1)}}$.

Ans: Given: ${\text{A}}(2,{\text{ 0, 3), B(0, 3, 2) and C(0, 0, 1)}}$.

${\text{Here, PA  =  PB,}}$

$\Rightarrow {\text{ (0 }} - {\text{ 2}}{{\text{)}}^2}{\text{  +  (y }} - {\text{ 0}}{{\text{)}}^2}{\text{  +  (z }} - {\text{ 3}}{{\text{)}}^2}{\text{  =  (0 }} - {\text{ 0}}{{\text{)}}^2}{\text{  +  (y }} - {\text{ 3}}{{\text{)}}^2}{\text{  +  (z }} - {\text{ 2}}{{\text{)}}^2}$

$\Rightarrow {\text{ z }} - {\text{ 3y  =  0    }}......{\text{(1)}}$

${\text{Similarly, PB  =  PC,}}$

$\Rightarrow {\text{ }}{{\text{y}}^2}{\text{  +  9 }} - {\text{ 6y  +  }}{{\text{z}}^2}{\text{  +  4 }} - 4z{\text{  =  }}{{\text{y}}^2}{\text{  +  }}{{\text{z}}^2}{\text{  +  1 }} - {\text{ 2z}}$

$\Rightarrow {\text{ 3y  +  z  =  6    }}......{\text{(2)}}$

${\text{Solving equation (1) and (2), we get}}$

${\text{y  =  1 and z  =  3}}$

$\therefore {\text{ Point P(0, 1, 3)}}{\text{.}}$ 

Objective Type Question:

Choose the correct answer out of four options in each of the Examples from $18 \,to\, 23$ (M.C.Q.)

Sample Question 18: The length of the foot of perpendicular drawn from the point ${\text{P(3, 4, 5)}}$ on y  -  axis is

(a) 10

(b) \[\sqrt {34}\]

(c) \[\sqrt {113}\]

(d) \[\sqrt {2}\]

Ans: Option (b)

Given: Point ${\text{P(3, 4, 5)}}{\text{.}}$

${\text{Distance between points P(3, 4, 5) and (0, 4, 0),}}$

${\text{ = }}\sqrt {{{(0{\text{ }} - 3)}^2}{\text{  +  (4 }} - {\text{ 4}}{{\text{)}}^2}{\text{  +  (0 }} - {\text{ 5}}{{\text{)}}^2}}$

$= {\text{ }}\sqrt {9{\text{  +  25}}}$

$= {\text{ }}\sqrt {34}$ 

Sample Question 19: What is the perpendicular distance of the point P(6, 7, 8) from xy  - plane?

(a)  8

(b)  7

(c)  6

(d) None of these

Ans: Option (a)

Given: P(6, 7, 8)

Let ${\text{L}}$ be the length of the foot of perpendicular drawn from the point ${\text{P(6, 7, 8) to xy  - }}$ plane. Then, the distance of the foot of the perpendicular will be given by ${\text{z  - }}$ coordinate.

Therefore, ${\text{L  =  8 units}}{\text{.}}$

Sample Question 20: L is the foot of the perpendicular drawn from a point P(6, 7, 8) on the xy  -  plane. What are the coordinates of point L ?

(a) (6, 0, 0)

(b) (6, 7, 0)

(c) (6, 0, 8)

(d) None of these

Ans: Option (b)

Given: L is the foot of the perpendicular drawn from a point P(6, 7, 8) to xy- plane.

Here, ${\text{L}}$ is the foot of the perpendicular drawn from a point ${\text{P(6, 7, 8) on the xy  -  plane}}{\text{.}}$\therefore, the ${\text{z  - }}$ coordinate will be zero. The ${\text{x  -  and y  - }}$ coordinates will remain the same but ${\text{z  - }}$ coordinate will be zero. Therefore, the coordinate of point ${\text{L}}$ are $(6,{\text{ 7, 0)}}{\text{.}}$

Sample question 21: L is the foot of the perpendicular drawn from a point P(6, 7, 8) on x -  axis. The coordinates of point L are

(a) (6, 0, 0)

(b) (0, 7, 0)

(c) (0, 0, 8)

(d). None of these

Ans: Option (a)

Given: L is the foot of the perpendicular drawn from a point P(6, 7, 8) on x -  axis,

Here, ${\text{L}}$ is the foot of the perpendicular drawn from a point ${\text{P(6, 7, 8) on the x  -  axis}}{\text{.}}$\therefore, the ${\text{y  -  and z  - }}$ coordinates will be zero. 

The ${\text{x  - }}$ coordinates will remain the same but ${\text{y  -  and z  - }}$ coordinate will be zero. Therefore, the coordinate of point ${\text{L}}$ are $(6,{\text{ 0, 0)}}{\text{.}}$

Sample Question 22: What is the locus of a point for which $y  =  0, z  =  0 ?$

(a).Equation of x-axis

(b). Equation of y-axis

(c). Equation of z-axis

(d). None of these

Ans: Option (a)

Given: ${\text{y  =  0, z  =  0}}{\text{.}}$

Since, on ${\text{x  - }}$ axis the point ${\text{y  =  0, z  =  0}}$ will always hold true, Therefore, the locus of point for which ${\text{y  =  0, z  =  0}}$ is the equation of ${\text{x - }}$ axis.

Sample Question 23: L is the foot of the perpendicular drawn from a point P(3, 4, 5) on xz  -  plane. What are the coordinates of point L.

(a) (3, 0, 0)

(b) (0, 4, 5)

(c) (3, 0, 5)

(d) (3, 4, 0)

Ans: Option  (c)

Given: L is the foot of the perpendicular drawn from a point P(3, 4, 5) on xz  -  plane.

Here, ${\text{L}}$ is the foot of the perpendicular drawn from a point ${\text{P(3, 4, 5) on xz  -  plane}}{\text{.}}$ Therefore, the ${\text{y  - }}$ coordinate will be zero. 

The ${\text{x  -  and z  - }}$ coordinates will remain the same but ${\text{y  - }}$ coordinate will be zero. Therefore, the coordinate of point ${\text{L}}$ are $(3,{\text{ 0, 5)}}{\text{.}}$

Fill in the blanks in Examples 24 to 28:

Sample Question 24: A line is parallel to $xy  -$ plane if all the points on the line have equal _____.

Ans: z- coordinate will be equal for all the points on line which are parallel to xy - plane.

Sample Question 25: The equation $x  =  b$ represents a plane parallel to _____ plane.

Ans: As, on ${\text{yz  - }}$ plane, ${\text{x  - }}$ coordinate is always zero. Therefore, ${\text{x  =  b}}$ also represents a plane parallel to ${\text{yz  - }}$ plane with distance ${\text{b}}$ from the origin.

Sample Question 26: Perpendicular distance of the point P(3, 5, 6)  from y  - axis is ____.

Ans: Given: Point ${\text{P(3, 5, 6)}}{\text{.}}$

Let ${\text{M}}$ be the point on ${\text{y  -  axis,}}$ The coordinates of  ${\text{M}}{\text{ are (0, 5,  0)}}{\text{.}}$

Therefore, the perpendicular distance of point ${\text{P(3, 5, 6) from y  - }}$ axis will be $\sqrt {{3^2}{\text{  +  }}{{\text{6}}^2}} {\text{  =  }}\sqrt {45} {\text{ units}}{\text{.}}$

Sample Question 27: L is the foot of the perpendicular drawn from a point P(3, 4, 5) on zx  -  plane.  The coordinates of L are _____ .

Ans: Given: L is the foot of the perpendicular drawn from a point P(3, 4, 5) on zx  -  plane.

Here, ${\text{L}}$ is the foot of the perpendicular drawn from a point ${\text{P(3, 4, 5) on zx  -  plane}}{\text{.}}$ therefore, the ${\text{y  - }}$ coordinate will be zero. 

The ${\text{x and z  - }}$ coordinates will remain the same but ${\text{y  = }}$ coordinate will be zero. Therefore, the coordinate of point ${\text{L}}$ are $(3,{\text{ 0, 5)}}{\text{.}}$

Sample Question 28: The length of the foot of perpendicular drawn from the point P(a, b, c) on the z - axis is _____.

Ans: Given: P(a, b, c) on z - axis.

The foot of perpendicular from point ${\text{P(a, b, c) on z - }}$ axis will be $(0,{\text{ 0,}}{\text{c)}}{\text{.}}$ Use the distance formula for ${\text{A(}}{{\text{x}}_1},{\text{ }}{{\text{y}}_1},{\text{ }}{{\text{z}}_1}){\text{ and B(}}{{\text{x}}_2},\,{{\text{y}}_2},{\text{ }}{{\text{z}}_2}),{\text{ AB  =  }}\sqrt {{{({{\text{x}}_2}{\text{ }} - {\text{ }}{{\text{x}}_1})}^2}{\text{  +  (}}{{\text{y}}_2}{\text{ }} - {\text{ }}{{\text{y}}_1}{)^2}{\text{  +  (}}{{\text{z}}_2}{\text{ }} - {\text{ }}{{\text{z}}_1}{)^2}} .$

The distance between points ${\text{P(a, b, c) and (0, 0, c)}}$ is $\sqrt {{{\text{a}}^2}{\text{  +  }}{{\text{b}}^2}} .$

Check whether the statements in Example from 29 to 37 are True or False:

Sample Question 29: The y  -  axis and z  -  axis, together determine a plane known as yz  -plane.

Ans: Given: The ${\text{y  -  axis and z  -  axis}}$, together determine a plane known as ${\text{yz  - }}$ plane.

Use the basic concepts of coordinate systems in three dimensional geometry.

The ${\text{y  -  axis and z  -  axis}}$ are generally known as ${\text{yz  - }}$ plane. The ${\text{x  - }}$ coordinate is zero in this plane. Therefore, it is ${\text{yz  - }}$ plane.

Hence, Answer is true.

Sample Question 30: The point (4, 5,  -  6) lies in the ${5^{{\text{th}}}}$ octant.

Ans: If ${\text{x  >  =  0, y  >  =  0 and z  <  0}}$ then the point lies in ${5^{{\text{th}}}}$ octant. Therefore, point $(4,{\text{ 5, }} - {\text{ 6)}}$ lies in ${5^{{\text{th}}}}$ octant.

Hence, Answer is False.

Sample Question 31: The x  - axis is the intersection of two planes xy- plane and xz- plane.

Ans: In a three dimensional coordinate geometry, the ${\text{x, y and z}}$axes are mutually perpendicular to each other. Therefore, ${\text{x  - }}$ axis is the intersection of two planes ${\text{xy  - }}$ plane and ${\text{xz  - }}$ plane.

Hence, Answer is True.

Sample Question 32: Three mutually perpendicular planes divide the space into $8$ octants.

Ans: In a three dimensional coordinate geometry, the ${\text{x, y and z}}$ axes are mutually perpendicular to each other. These divide the space into $8$octants.

Hence, Answer is True.

Sample Question 33: The equation of the plane z = 6 represents a plane parallel to the xy- plane, having a z- intercept of 6 units.

Ans: As, on ${\text{xy  - }}$ plane, ${\text{z  - }}$ coordinate is always zero. Therefore, ${\text{z  =  6}}$ also represents a plane parallel to ${\text{xy  - }}$ plane with distance $6$ from the origin.

Hence, Answer is True.

Sample Question 34: The equation of the plane x  =  0 represents the yz - plane.

Ans: As, on ${\text{yz  - }}$ plane, ${\text{x  - }}$ coordinate is always zero. Therefore, the equation of the plane ${\text{x  =  0}}$ represents the ${\text{yz  - }}$ plane.

Hence, Answer is True.

Sample Question 35: The point on the x- axis with x- coordinate equal to ${{\text{x}}_{\text{0}}}$ is written as $({{\text{x}}_0},{\text{ 0, 0)}}{\text{.}}$

Ans: Given: The point on the ${\text{x  - }}$ axis with ${\text{x  - }}$ coordinate equal to ${{\text{x}}_{\text{0}}}$ is written as $({{\text{x}}_0},{\text{ 0, 0)}}{\text{.}}$

For point on the ${\text{x  - }}$ axis with ${\text{x  - }}$ coordinate equal to ${{\text{x}}_{\text{0}}}$. The coordinates of the point will be ${\text{x  =  }}{{\text{x}}_0},{\text{ y  =  0, z  =  0 that is }}({{\text{x}}_0},{\text{ 0, 0)}}{\text{.}}$

Hence, Answer is True.

Sample Question 36: ${\text{x  =  }}{{\text{x}}_0}$ represents a plane parallel to the yz -plane.

Ans: As, on ${\text{yz  - }}$ plane, ${\text{x  - }}$ coordinate is always zero. Therefore, ${\text{x  =  }}{{\text{x}}_0}$ also represents a plane parallel to ${\text{yz  - }}$ plane with distance ${{\text{x}}_0}$ from origin.

Hence, answer is True.

Match each item given under the column C1 to its correct answer given under column C2.

Sample Question 37: 

Ans: Given: 

Column ${{\text{C}}_1}$ and ${{\text{C}}_2}.$

Use the basic concepts of three dimensional geometry. Midpoint formula and distance formula.

(a). Here, A(3,-5,7), B(-1,7,-6), C(x, y, z) be the vertices of a $\Delta$ ABC with centroid 0, 0,0

$\therefore {\text{ (0, 0, 0)  =  }}\left( {\dfrac{{{\text{3 }} - {\text{ 1  +  x}}}}{3},{\text{ }}\dfrac{{ - {\text{ 5  +  7  +  y}}}}{3},{\text{ }}\dfrac{{7{\text{ }} - {\text{ 6  +  z}}}}{3}} \right)$

$\Rightarrow {\text{ }}\dfrac{{{\text{x  +  2}}}}{3}{\text{  =  0, }}\dfrac{{{\text{y  +  2}}}}{3}{\text{  =  0, }}\dfrac{{{\text{z  +  1}}}}{3}{\text{  =  0}}$

$\therefore {\text{ x  =  }} - {\text{ 2, y  =  }} - {\text{ 2 and z  =  }} - {\text{ 1}}{\text{.}}$ 

(b). Here 

Let ABC be the given $\Delta$ and DEF be the mid - points of the sides BC, CA, AB, respectively.

Therefore, centroid of the $\Delta$ ABC  =  centroid of $\Delta$ DEF.

$\therefore$ Centroid of $\Delta$ DEF  = 

$\left( {\dfrac{{1{\text{  +  3 }} - {\text{ 1}}}}{3},\,\dfrac{{2{\text{  +  0  +  1}}}}{3},{\text{ }}\dfrac{{ - \,{\text{3  +  1 }} - {\text{ 4}}}}{3}} \right){\text{  =  (1, 1, }} - {\text{ 2)}}$ 

(c). Here, 

Mid - point of diagonal AC  

=$\left( {\dfrac{{{\text{3  +  2}}}}{2},{\text{ }}\dfrac{{ - {\text{ 1  +  3}}}}{2},{\text{ }}\dfrac{{ - {\text{ 1 }} - {\text{ 2}}}}{2}} \right){\text{  =  }}\left( {\dfrac{{\text{5}}}{2},1,\dfrac{{ - 3}}{2}} \right)$

Mid - point of diagonal BD  

=$\left( {\dfrac{{{\text{5  +  0}}}}{2},{\text{ }}\dfrac{{ - {\text{ 4  +  6}}}}{2},{\text{ }}\dfrac{{0{\text{ }} - {\text{ 3}}}}{2}} \right){\text{  =  }}\left( {\dfrac{{\text{5}}}{2},1,\dfrac{{ - 3}}{2}} \right)$

$\therefore$ Diagonals of parallelogram bisect each other. 

(d). Here,

$|{\text{AB|  =  }}\sqrt {{{(2{\text{ }} - {\text{ 1)}}}^2}{\text{  +  (}} - {\text{ 4  +  1}}{{\text{)}}^2}{\text{  +  (5 }} - {\text{ 3}}{{\text{)}}^2}} {\text{  =  }}\sqrt {14}$

$|{\text{BC|  =  }}\sqrt {{{(5{\text{ }} - {\text{ 2)}}}^2}{\text{  +  (}} - {\text{ 13  +  4}}{{\text{)}}^2}{\text{  +  (11 }} - {\text{ 5}}{{\text{)}}^2}} {\text{  =  3}}\sqrt {14}$

$|{\text{AC|  =  }}\sqrt {{{({\text{5 }} - {\text{ 1)}}}^2}{\text{  +  (}} - {\text{ 13  +  1}}{{\text{)}}^2}{\text{  +  (11 }} - {\text{ 3}}{{\text{)}}^2}} {\text{  =  4}}\sqrt {14}$

$\Rightarrow {\text{ |AB|  +  |BC|  =  |AC|}}$

A, B and C are collinear.

(e). Here,

${\text{AB  =  }}\sqrt {4{\text{  +  9  +  36}}} {\text{  =  7}}$

${\text{BC  =  }}\sqrt {{\text{36  +  4  +  9}}} {\text{  =  7}}$

${\text{CA  =  }}\sqrt {64{\text{  +  25  +  9}}} {\text{  =  7}}\sqrt 2$

$\Rightarrow {\text{ A}}{{\text{B}}^2}{\text{  +  B}}{{\text{C}}^2}{\text{  = A}}{{\text{C}}^2}$ 

Therefore, the correct matches are $({\text{a) }} \to {\text{ (ii), (b) }} \to {\text{ (iv), (c) }} \to {\text{ (i), (d) }} \to {\text{ (v), (e) }} \to {\text{ (iii)}}$

Short Answers Type Question:

1. Locate the following points:

(i) ${\text{ }}(1, - 1,3)$ 

Ans:

Each plane divides this space in two parts and these three coordinate planes together divide the space in eight regions called octants.

Locate the point ${\text{P}}.$

The point ${\text{P}}(1, - 1,3)$ is located in the $IV$ octant.

(ii) ${\text{ }}( - 1,2,4)$ 

Ans:

Each plane divides this space in two parts and these three coordinate planes together divide the space in eight regions called octants.

Locate the point ${\text{P}}.$

The point ${\text{P}}( - 1,2,4)$ is located in the$Il$ octant.

(iii) ${\text{ }}( - 2, - 4, - 7)$ 

Ans: 

Each plane divides this space in two parts and these three coordinate planes together divide the space in eight regions called octants.

Locate the point ${\text{P}}.$

The point ${\text{P}}( - 2, - 4, - 7)$ is located in the $VII$ octant.

(iv) ${\text{ }}\left( { - 4,2, - 5} \right)$ 

Ans:

Each plane divides this space in two parts and these three coordinate planes together divide the space in eight regions called octants.

Locate the point $P.$

The point $P{\text{ }}\left( { - 4,2, - 5} \right)$ is located in the ${\text{Vl}}$ octant.

2. Name the octant in which each of the following points lies.

(i) ${\text{ }}\left( {1,2,3} \right)$ 

Ans:

Each plane divides this space in two parts and these three coordinate planes together divide the space in eight regions called octants.

Locate the point ${\text{P}}.$

The point $P{\text{ }}\left( {1,2,3} \right)$ is located in the $I$ octant.

(ii) ${\text{ }}(4, - 2,3)$ 

Ans:

Each plane divides this space in two parts and these three coordinate planes together divide the space in eight regions called octants.

Locate the point $P.$

The point ${\text{P}}(4, - 2,3)$ is located in the $IV$ octant.

(iii) ${\text{ }}(4, - 2,-5)$ 

Ans:

Each plane divides this space in two parts and these three coordinate planes together divide the space in eight regions called octants.

Locate the point${\text{P}}$. 

The point $P(4, - 2, - 5)$ is located in the $VIII$ octant.

(iv) ${\text{ }}(4, 2,-5)$ 

Ans: 

Each plane divides this space in two parts and these three coordinate planes together divide the space in eight regions called octants.

Locate the point ${\text{P}}.$

The point $P\left( {4,2, - 5} \right)$ is located in the ${\text{V}}$ octant.

(v) ${\text{ }}(-4,2,5)$ 

Ans:

Each plane divides this space in two parts and these three coordinate planes together divide the space in eight regions called octants.

Locate the point ${\text{P}}.$]

The point ${\text{P}}( - 4,2,5)$ is located in the $II$ octant.

(vi) ${\text{ }}( - 3, - 1,6)$ 

Ans:

Each plane divides this space in two parts and these three coordinate planes together divide the space in eight regions called octants.

Locate the point ${\text{P}}.$

The point ${\text{P}}( - 3, - 1,6)$ is located in the $III$octant.

(vii) ${\text{P}}( 2, - 4,-7)$ 

Ans:

Each plane divides this space in two parts and these three coordinate planes together divide the space in eight regions called octants.

Locate the point $P.$

The point $P(2, - 4, - 7)$ is located in the $VIII$octant.

(viii) ${\text{ }}( - 4,2, - 5)$ 

Ans:

Each plane divides this space in two parts and these three coordinate planes together divide the space in eight regions called octants.

Locate the point ${\text{P}}$

The point ${\text{P}}( - 4,2, - 5)$ is located in the ${\text{Vl}}$ octant.

3. Let $A,{\kern 1pt} {\kern 1pt} {\kern 1pt} B,{\kern 1pt} {\kern 1pt} {\kern 1pt} C$ be the feet of perpendiculars from a point ${\text{P}}$ on the $x,{\kern 1pt} {\kern 1pt} {\kern 1pt} y,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} z -$ axis respectively. Find the coordinates of $A,{\kern 1pt} {\kern 1pt} {\kern 1pt} B$ and ${\text{C}}$in each of the following where the point${\text{P}}$ is:

(i)  $(3,4,2)$

Ans:

Each plane divides this space in two parts and these three coordinate planes together divide the space in eight regions called octants.

Locate the points.

The coordinates of $A$ are $(3,0,0)$

The coordinates of $B$ are $(0,4,0)$

The coordinates of $C$ are $(0,0,2)$

(ii) ( - 5,3,7)

Ans:

Each plane divides this space in two parts and these three coordinate planes together divide the space in eight regions called octants.

Locate the points.

The coordinates of ${\text{A}}$ are $( - 5,0,0)$

The coordinates of ${\text{B}}$ are $(0,3,0,)$

The coordinates of $C$ are $(0,0,7)$

(iii) (4, - 3, - 5)

Ans:

Each plane divides this space in two parts and these three coordinate planes together divide the space in eight regions called octants.

Locate the points. 

The coordinates of $A$ are $(4,0,0)$

The coordinates of $B$ are $(0, - 3,0)$

The coordinates of $C$ are $(0,0, - 5)$

4. Let $A,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} B,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} C$ be the feet of perpendiculars from a point ${\text{P}}$ on the $xy,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} yz$ and $zx$ planes respectively. Find the coordinates of $A,{\kern 1pt} {\kern 1pt} {\kern 1pt} B,{\kern 1pt} {\kern 1pt} {\kern 1pt} C$ in each of the following where the point ${\text{P}}$ is
(i) $\left( {3,4,5} \right)$

Ans:

Each plane divides this space in two parts and these three coordinate planes together divide the space in eight regions called octants.

Locate the points.

The coordinates of $A$ are$(3,{\kern 1pt} 4,{\kern 1pt} 0)$]

The coordinates of $B$ are $(0,{\kern 1pt} 4,{\kern 1pt} 5)$

The coordinates of $C$ are$(3,{\kern 1pt} 0,{\kern 1pt} 5)$

(ii) ( - 5,3,7)

Ans:

Each plane divides this space in two parts and these three coordinate planes together divide the space in eight regions called octants.

Locate the points.

The coordinates of $A$ are$( - 5,{\kern 1pt} 3,{\kern 1pt} 0)$

The coordinates of $B$ are $(0,{\kern 1pt} 3,{\kern 1pt} 7)$

The coordinates of $C$ are $( - 5,{\kern 1pt} 0,{\kern 1pt} 7)$

(iii) $\left( {4, - 3, - 5} \right).$

Ans:

Each plane divides this space in two parts and these three coordinate planes together divide the space in eight regions called octants.

Locate the points. 

The coordinates of $A$ are$(4, - 3,0)$

The coordinates of $B$ are$(0, - 3, - 5){\text{}}$

The coordinates of $C$ are${\text{C}}(4,0, - 5)$

5. How far apart are the points $(2,0,0)$ and $( - 3,0,0)$

Ans: Given:The points $(2,0,0)$ and $( - 3,0,0)$

The distance between two points $P\left( {{x_1},{y_1},{z_1}} \right)$ and $Q\left( {{x_2},{y_2},{z_2}} \right)$ is given by$PQ = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}}$.

Given points are $(2,0,0)$ and $( - 3,0,0)$

Distance between the given points

$= \sqrt {{{(2 + 3)}^2} + {{(0 - 0)}^2} + {{(0 - 0)}^2}}$

$= \sqrt {25}$

$= 5$

Hence, the required distance is $5.$

6. Find the distance from the origin to $\left( {6,6,7} \right).$

Ans: Given: The origin to $\left( {6,6,7} \right).$

The distance between two points $P\left( {{x_1},{y_1},{z_1}} \right)$ and $Q\left( {{x_2},{y_2},{z_2}} \right)$ is given by$PQ = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}}$.

Coordinates of the origin are $(0,0,0)$

Distance from $(0,0,0)$to $(6,6,7)$

$D = \sqrt {{{(6 - 0)}^2} + {{(6 - 0)}^2} + {{(7 - 0)}^2}}$

$= \sqrt {36 + 36 + 49}$

$= \sqrt {121}$

$= 11$units. 

Hence, the required distance is $11$units.

7.Show that if ${x^2} + {y^2} = 1,$ then the point $\left( {x,y,\sqrt {1 - {x^2} - {y^2}} } \right)$ is at a distance $1$unit from the origin.

Ans: Given: Point $\left( {x,y,\sqrt {1 - {x^2} - {y^2}} } \right)$

Given point is $\left( {x,y,\sqrt {1 - {x^2} - {y^2}} } \right)$

Distance between the origin and the point is

$D = \sqrt {{{(x - 0)}^2} + {{(y - 0)}^2} + {{\left( {\sqrt {1 - {x^2} - {y^2}}  - 0} \right)}^2}}$

$= \sqrt 1  = 1$

Hence, proved.

8. Show that the point $A(1, - 1,3),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} B(2, - 4,5)$ and $(5, - 13,11)$ are collinear.

Ans: Given: ${\text{A}}(1, - 1,3),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{B}}(2, - 4,5)$ and$(5, - 13,11)$

Examine the points.

The distance between points $A$ and $B$ is $\sqrt {{{(2 - 1)}^2} + {{( - 4 + 1)}^2} + {{(5 - 3)}^2}}$

$= \sqrt {{{(1)}^2} + {{( - 3)}^2} + {{(2)}^2}}$

$= \sqrt {1 + 9 + 4}$

$= \sqrt {14}$

The distance between points $B$ and $C$ is $\sqrt {{{(5 - 2)}^2} + {{( - 13 + 4)}^2} + {{(11 - 5)}^2}}$

$= \sqrt {{{(3)}^2} + {{( - 9)}^2} + {{(6)}^2}}$

Solve further, $\sqrt {9 + 81 + 36}$

$= \sqrt {126}$

$= 3\sqrt {14}$

The distance between points $A$ and $C$ is $\sqrt {{{(5 - 1)}^2} + {{( - 13 + 1)}^2} + {{(11 - 3)}^2}}$

$= \sqrt {16 + 144 + 64}$

$= \sqrt {224}$

i.e. $4\sqrt {14}$

Therefore,

${\text{AB + BC = AC}}$

The points ${\text{A, B}},$ and ${\text{C}}$ are collinear.

9. Three consecutive vertices of a parallelogram $ABCD$ are $A(6, - 2,4),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} B(2,4, - 8),{\kern 1pt} \,{\kern 1pt} {\kern 1pt} C( - 2,2,4)$. Find the coordinates of the fourth vertex.

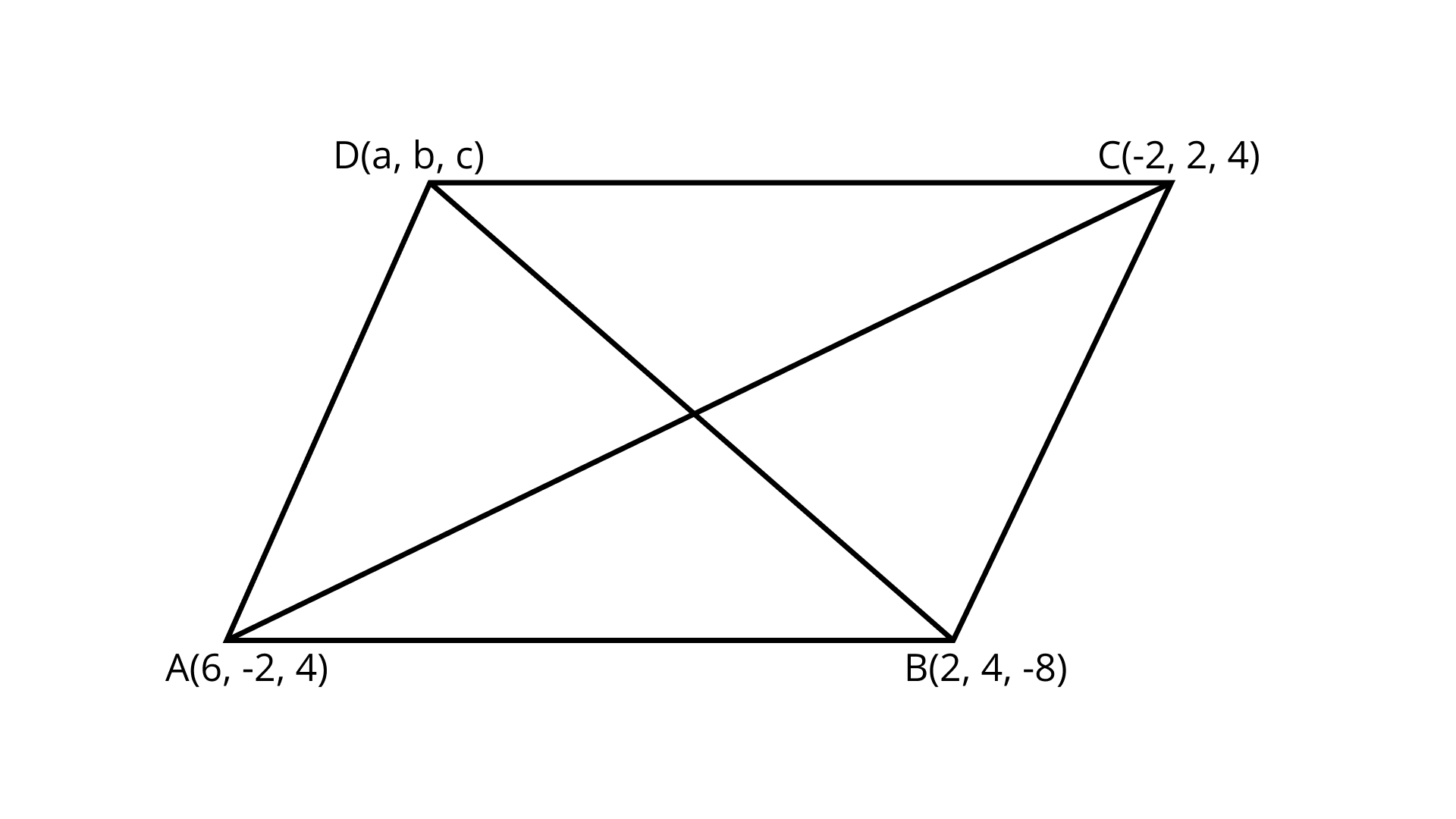
$= (2,0,4)$

Ans: Given:${\text{A}}(6, - 2,4),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{B}}(2,4, - 8),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{C}}( - 2,2,4)$

To find: Coordinates of the fourth vertex.

The diagonals of a parallelogram bisect each other.

Midpoint of diagonal

${\text{AC}} = \left( {\dfrac{{6 - 2}}{2},\dfrac{{ - 2 + 2}}{2},\dfrac{{4 + 4}}{2}} \right)$

And the midpoint of diagonal $BD$                            

$= \left( {\dfrac{{a + 2}}{2},\dfrac{{b + 4}}{2},\dfrac{{c - 8}}{2}} \right)$

$\dfrac{{a + 2}}{2} = 2$

$\Rightarrow a = 2$

And

$\dfrac{{b + 4}}{2} = 0$

$\Rightarrow b =  - 4$

$\dfrac{{c - 8}}{2} = 4$

$\Rightarrow c = 16$

Hence, the required coordinates are $\left( {2, - 4,16} \right).$

10. Show that the triangle $ABC$ with vertices $A\left( {0,4,1} \right), {\kern 1pt} B\left( {2,3,-1} \right)$ and $C\left( {4,5,0} \right)$ is right angled.

Ans: Given:

$\mathrm{A}(0,4,1), \mathrm{B}(2,3,-1)$

$\mathrm{C}(4,5,0)$

Given vertices are ${\text{A}}\left( {0,4,1} \right),{\text{ }}{\kern 1pt} {\text{B}}\left( {2,3,-1} \right)$ and ${\text{C}}(4,5,0)$

So,${\text{AB  = }}\sqrt {{{(2 - 0)}^2} + {{(3 - 4)}^2} + {{( - 1 - 1)}^2}}$

$= \sqrt {4 + 1 + 4}$

$= \sqrt 9$

$= 3$

Also,

${\text{BC}} = \sqrt {{{(4 - 2)}^2} + {{(5 - 3)}^2} + {{(0 + 1)}^2}} {\text{ }}$

$= \sqrt {4 + 4 + 1}$

$= \sqrt 9$

$= 3$

Also,

${\text{AC}} = \sqrt {{{(4 - 0)}^2} + {{(5 - 4)}^2} + {{(0 - 1)}^2}}$

$= \sqrt {16 + 1 + 1}$

$= \sqrt {18}$

For right angled triangle ${(AB)^2} + {(BC)^2} = {(AC)^2}$

${(3)^2} + {(3)^2} = {(\sqrt {18} )^2}$

So ${\text{A}}{{\text{B}}^2} + {\text{B}}{{\text{C}}^2} = {\text{A}}{{\text{C}}^2}$

Hence, $\vartriangle {\text{ABC}}$ is a right angled triangle.

11. Find the third vertex of triangle whose centroid is origin and two vertices are $\left( {2,4,6} \right)$ and $\left( {0,-2,-5} \right).$

Ans: Given:Triangle ${\text{ABC}}$

Two vertices ${\text{B}} = \left( {2,4,6} \right)$ and ${\text{C}} = \left( {0,-2,-5} \right).$

Let the coordinates of the third vertex ${\text{A}}$ be $(a,b,c)$. 

Since the centroid is at origin $(0,0,0)$

Hence, the $x$ coordinate is $\dfrac{{a + 2 + 0}}{3} = 0$

$a + 2 = 0$

$\Rightarrow a =  - 2$

Hence, the $y$ coordinate is $\dfrac{{b + 4 - 2}}{3} = 0$

$b + 2 = 0$

$\Rightarrow b =  - 2$

Hence, the $z$coordinate is $\dfrac{{c + 6 - 5}}{3} = 0$

$c + 1 = 0$

$\Rightarrow c =  - 1$

The third vertex of the triangle is $( - 2, - 2, - 1)$

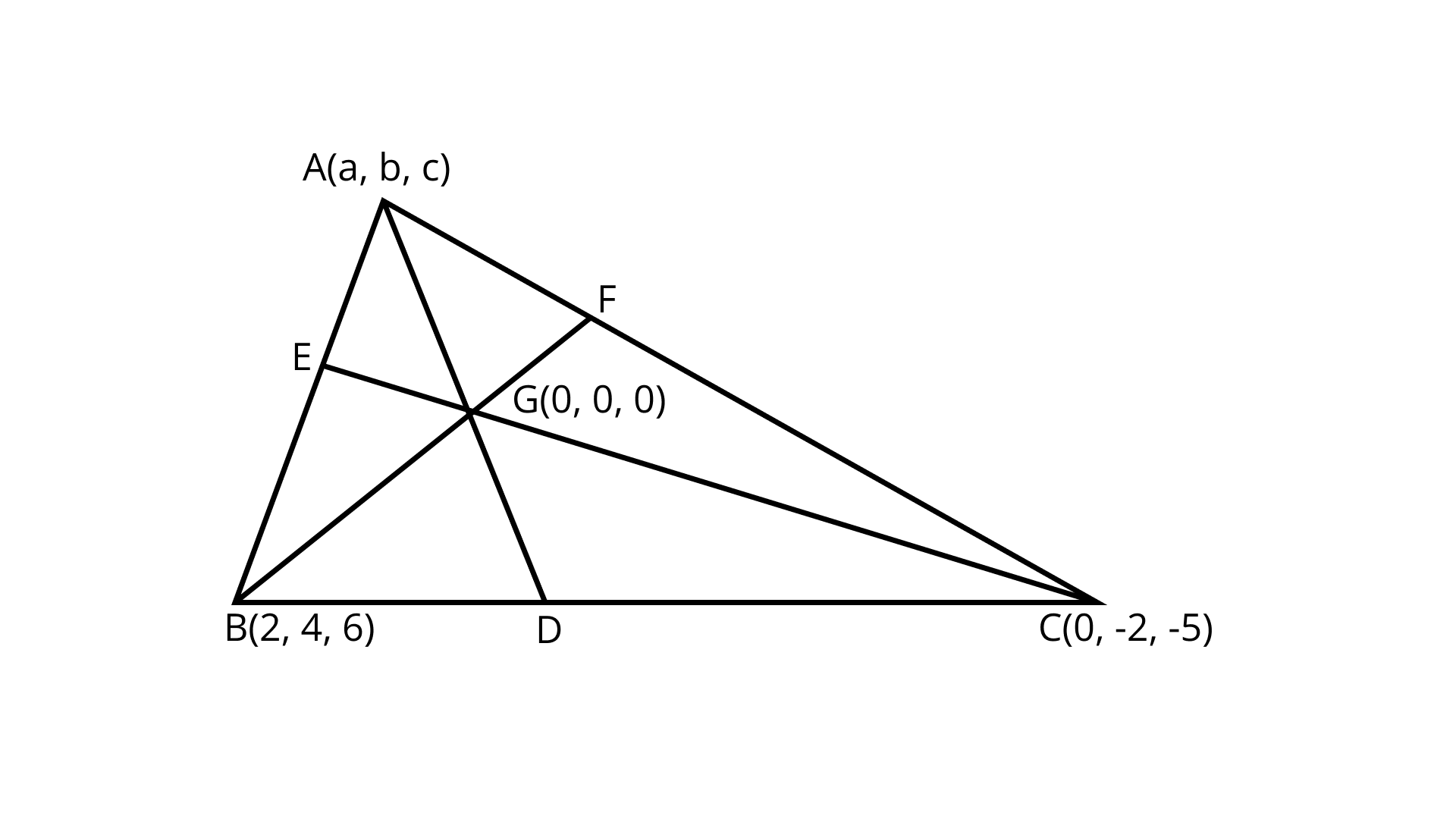
12. Find the centroid of a triangle, the mid-point of whose sides are $D\left( {1,2,-3} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E\left( {3,0,1} \right)$ and $F\left( {-1,1,-4} \right).$

Ans: Given: In Triangle $ABC$

Midpoint $D\left( {1,{\text{ }}2,-{\text{ }}3} \right)$

$E\left( {3,0,1} \right)$

$F\left( {-1,1,-4} \right).$

Let the coordinates of the vertices of $\vartriangle {\text{ABC}}$be ${\text{A}}\left( {{x_1},{y_1},{z_1}} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{B}}\left( {{x_2},{y_{{2^\prime }}},{z_2}} \right)$ and ${\text{C}}\left( {{x_3},{y_3},{z_3}} \right)$

Midpoint of $BC = (1,2, - 3)$

$1 = \dfrac{{{x_2} + {x_3}}}{2}$

${x_2} + {x_3} = 2$$.....{\text{(1)}}$

$2 = \dfrac{{{y_2} + {y_3}}}{2}$

${y_2} + {y_3} = 4$$.....(2)$

Similarly,

$- 3 = \dfrac{{{z_2} + {z_3}}}{2}$

${z_2} + {z_3} =  - 6$$.....(3)$

Midpoint of ${\text{AB}} = (3,0,1)$

$3 = \dfrac{{{x_1} + {x_2}}}{2}$

${x_1} + {x_2} = 6$$.....(4)$

So,

$0 = \dfrac{{{y_1} + {y_2}}}{2}$

${y_1} + {y_2} = 0$$.....(5)$

Similarly,

$1 = \dfrac{{{z_1} + {z_2}}}{2}$

${z_1} + {z_2} = 2$$.....(6)$

Similarly, midpoint of ${\text{AC}} = ( - 1,1, - 4)$

$- 1{\text{  = }}\dfrac{{{x_1} + {x_3}}}{2}$

${x_1} + {x_3} =  - 2$$.....(7)$

Similarly,

$1 = \dfrac{{{y_1} + {y_3}}}{2}$

${y_1} + {y_3} = 2$$.....(8)$

So,

$- 4 = \dfrac{{{z_1} + {z_3}}}{2}$

${z_1} + {z_3} =  - 8$$.....(9)$

Adding the equation of $(1),\,{\kern 1pt} {\kern 1pt} (4){\kern 1pt} {\kern 1pt} {\kern 1pt} a{\text{nd}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (7)$ get

$2{x_1} + 2{x_2} + 2{x_3} = 2 + 6 - 2 = 6$

${x_1} + {x_2} + {x_3} = 3$

$6 + {x_3} = 3$

$\Rightarrow {x_3} =  - 3$

Again,

${x_1} + 2 = 3$

${x_1} = 1$

Let,

${x_2} - 2 = 3$

${x_2} = 5$

So, ${x_1} = 1,{x_2} = 5$ and ${x_3} =  - 3.$

Similarly, 

Adding the equation $(2),{\kern 1pt} {\kern 1pt} {\kern 1pt} (5),\,{\kern 1pt} a{\text{nd}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (8)$get

$2\left( {{y_1} + {y_2} + {y_3}} \right) = 4 + 0 + 2 = 6$

${y_1} + {y_2} + {y_3} = 3$

${y_1} + 4 = 3$

${y_1} =  - 1$

$0 + {y_3} = 3$

${y_3} = 3$

${y_2} + 2 = 3$

$\Rightarrow {y_2} = 1$

So, ${y_1} =  - 1,{\kern 1pt} {\kern 1pt} {y_2} = 1,{\kern 1pt} {\kern 1pt} {y_3} = 3$

Adding the equation $(3),{\kern 1pt} {\kern 1pt} {\kern 1pt} (6){\kern 1pt} {\kern 1pt} \,a{\text{nd}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (8)$get

$2\left( {{z_1} + {z_2} + {z_3}} \right) =  - 6 + 2 - 8 =  - 12$

${z_1} + {z_2} + {z_3} =  - 6$

${z_1} - 6 =  - 6$

${z_1} = 0$

$2 + {z_3} =  - 6$

${z_3} =  - 8$

${z_3} =  - 8$

${z_2} - 8 =  - 6$

$\Rightarrow {z_2} = 2$

And

${z_1} = 1,{\kern 1pt} {\kern 1pt} {z_2} = 1,{\kern 1pt} {\kern 1pt} {z_3} =  - 8.$

So, the points are ${\text{A}}(1, - 1,0),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{B}}(5,1,2)$ and ${\text{C}}( - 3,3, - 8)$.

Centroid of the triangle

$G = \left( {\dfrac{{1 + 5 - 3}}{3},\dfrac{{ - 1 + 1 + 3}}{3},\dfrac{{0 + 2 - 8}}{3}} \right)$

$= (1,1, - 2)$

Hence, the required coordinates $\left( {1,1, - 2} \right).$

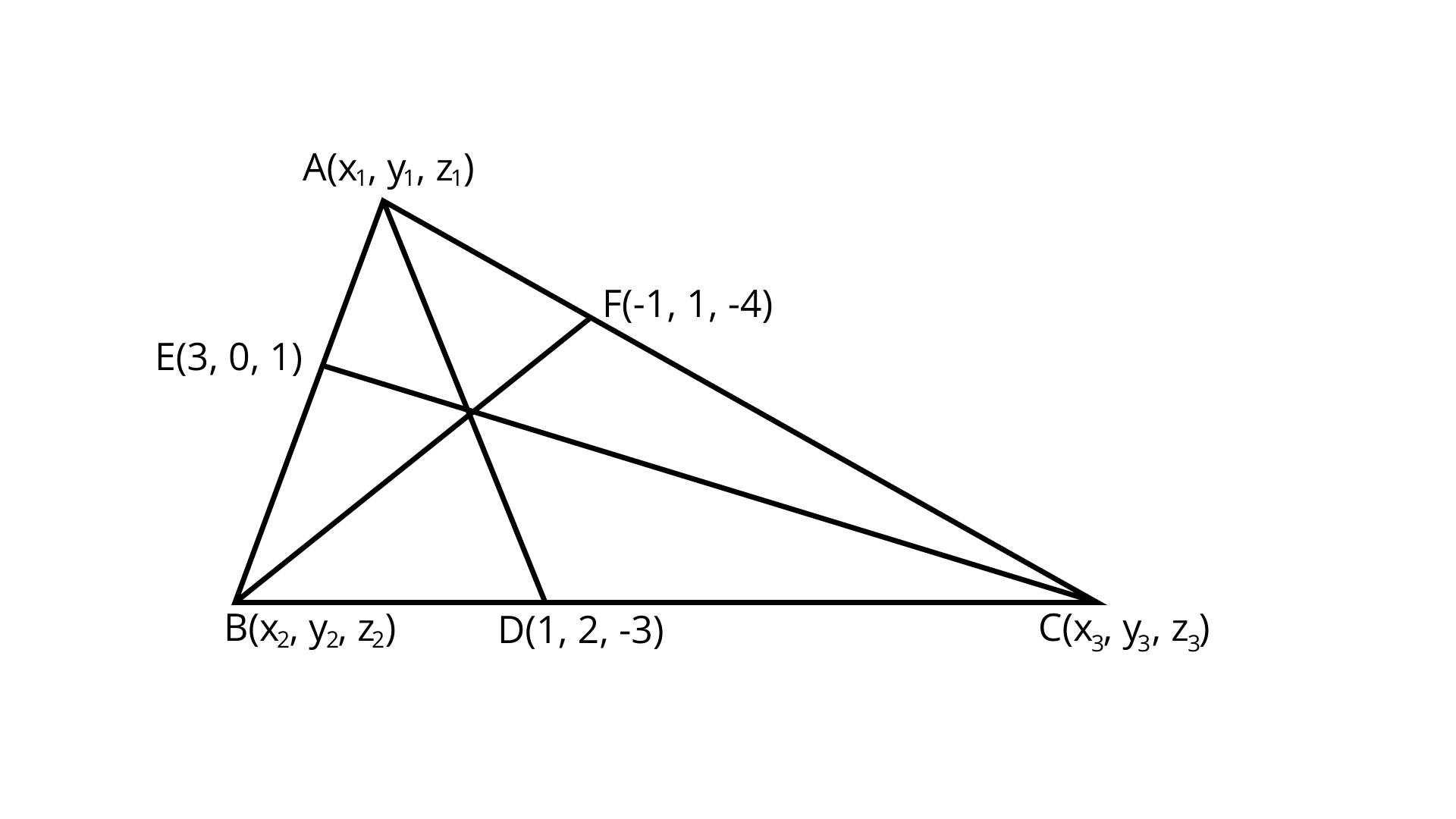
13.The mid-points of the sides of a triangle are $\left( {5,7,11} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {0,8,5} \right)$ and $\left( {2, 3,-1} \right).$ Find its vertices.

Ans: Given:In Triangle $ABC$

Midpoints are $\left( {5,7,11} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {0,8,5} \right)$ and $\left( {2,{\text{ }}3,-1} \right).$

Let the coordinates of the vertices be ${\text{A}}\left( {{x_1},{y_1},{z_1}} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{B}}\left( {{x_{{2^\prime }}}{y_{{2^\prime }}}{z_2}} \right)$ and ${\text{C}}\left( {{x_3},{y_3},{z_3}} \right)$ respectively.

Since ${\text{D}}(5,7,11)$ is the midpoint of ${\text{BC}}$ 

$5 = \dfrac{{{x_2} + {x_3}}}{2}$

${x_2} + {x_3} = 10$$.....(1)$

$7 = \dfrac{{{y_2} + {y_3}}}{2}$

${y_2} + {y_3} = 14$$.....(2)$

$11 = \dfrac{{{z_2} + {z_3}}}{2}$

${z_2} + {z_3} = 22$$.....(3)$

${\text{E}}(0,8,5)$ is the midpoint of ${\text{AB}}$

$0 = \dfrac{{{x_1} + {x_2}}}{2}$

${x_1} + {x_2} = 0$$.....(4)$

$8 = \dfrac{{{y_1} + {y_2}}}{2}$

${y_1} + {y_2} = 16$$.....(5)$

$5 = \dfrac{{{z_1} + {z_2}}}{2}$

${z_1} + {z_2} = 10$$.....(6)$

Similarly, $F(2,3, - 1)$ is the midpoint of $AC$

$2 = \dfrac{{{x_1} + {x_3}}}{2}$

${x_1} + {x_3} = 4$$.....(7)$

$3 = \dfrac{{{y_1} + {y_3}}}{2}$

${y_1} + {y_3} = 6$$.....(8)$

and $- 1 = \dfrac{{{z_1} + {z_3}}}{2}$

${z_1} + {z_3} =  - 2$$.....(9)$

Adding the equation $(1),{\kern 1pt} {\kern 1pt} {\kern 1pt} (4){\kern 1pt} {\kern 1pt} {\text{and}}{\kern 1pt} {\kern 1pt} (7)$

$2\left( {{x_1} + {x_2} + {x_3}} \right) = 10 + 0 + 4$

${x_1} + {x_2} + {x_3} = 7$$.....(10)$

Subtracting $(1)$ from $(10)$

${x_1} = 7 - 10 =  - 3$

Subtracting $(4)$ from $(10)$

${x_3} = 7 - 0 = 7$

Subtracting $(7)$ from $(10)$

${x_2} = 7 - 4 = 3$

Adding the equation $(2),{\kern 1pt} {\kern 1pt} (5){\kern 1pt} {\kern 1pt} {\text{and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (8)$

$2\left( {{y_1} + {y_2} + {y_3}} \right) = (14 + 16 + 6)$

${y_1} + {y_2} + {y_3} = 18$$.....(11)$

Subtracting $(2)$ from $(11)$

${y_1} = 18 - 14 = 4$

Subtracting $(5)$from $(11)$

${y_3} = 18 - 16 = 2$

Subtracting$(8)$ from $(11)$

${y_2} = 18 - 6 = 12$

Now adding the equation$(3),{\kern 1pt} {\kern 1pt} (6){\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} (9)$

$2\left( {{z_1} + {z_2} + {z_3}} \right) = 22 + 10 - 2$

${z_1} + {z_2} + {z_3} = 15$$.....(12)$

Subtracting $(3)$ from $(12)$

${z_1} = 15 - 22 =  - 7$

Subtracting $(6)$ from $(12)$

${z_3} = 15 - 10 = 5$

Subtracting $(9)$ from $(12)$

${z_2} = 15 + 2 = 17$

So, the required coordinates are ${\text{A}}\left( {{x_1},{y_1},{z_1}} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{B}}\left( {{x_2},{y_2},{z_2}} \right)$ and ${\text{C}}\left( {{x_3},{y_3},{z_3}} \right).$

That is ${\text{A}}( - 3,4, - 7),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{B}}(3,12,17)$ and ${\text{C}}(7,2,5)$.

14. Three vertices of a Parallelogram $ABCD$ are $A\left( {1,2,3} \right), B\left( {- 1,-2,-1} \right)$ and $C\left( {2,3,2} \right).$Find the fourth vertex $D$

Ans: Given: In parallelogram $ABCD$

${\text{A}}\left( {1,2,3} \right),{\text{ B}}\left( {-{\text{ }}1,-2,-1} \right)$ and$C\left( {2,3,2} \right).$

Let the coordinates of ${\text{D}}$be $\left( {a,{\kern 1pt} {\kern 1pt} {\kern 1pt} b,{\kern 1pt} {\kern 1pt} {\kern 1pt} c} \right).$

The diagonals of a parallelogram bisect each other.

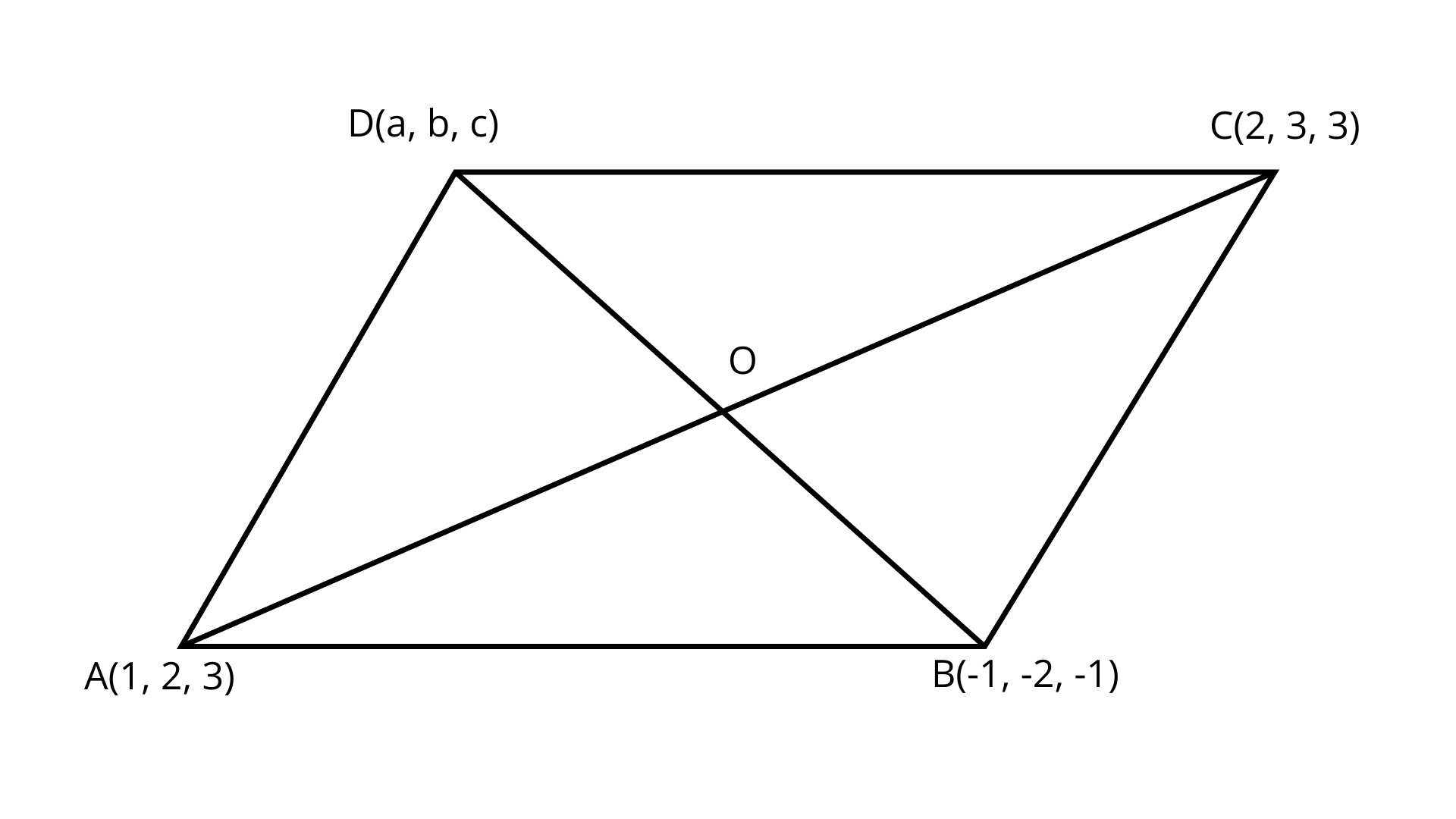
Midpoint of ${\text{AC}}$

${\text{O}} = \left( {\dfrac{{1 + 2}}{2},\dfrac{{2 + 3}}{2},\dfrac{{3 + 2}}{2}} \right)$ 

$= \left( {\dfrac{3}{2},\dfrac{5}{2},\dfrac{5}{2}} \right)$

Midpoint of $BD$

${\text{O}} = \left( {\dfrac{{a - 1}}{2},\dfrac{{b - 2}}{2},\dfrac{{c - 1}}{2}} \right)$

Equating the corresponding coordinate,

$\dfrac{{a - 1}}{2} = \dfrac{3}{2}$

$\Rightarrow a = 4$

$\dfrac{{b - 2}}{2} = \dfrac{5}{2}$

$\Rightarrow b = 7$

$\dfrac{{c - 1}}{2} = \dfrac{5}{2}$

$\Rightarrow c = 6$

Hence, the coordinates of ${\text{D}} = (4,7,6).$

15. Find the coordinate of the points which trisect the line segment joining the points $A\left( {2,1,-3} \right)$ and$B\left( {5,-8,3} \right)$.

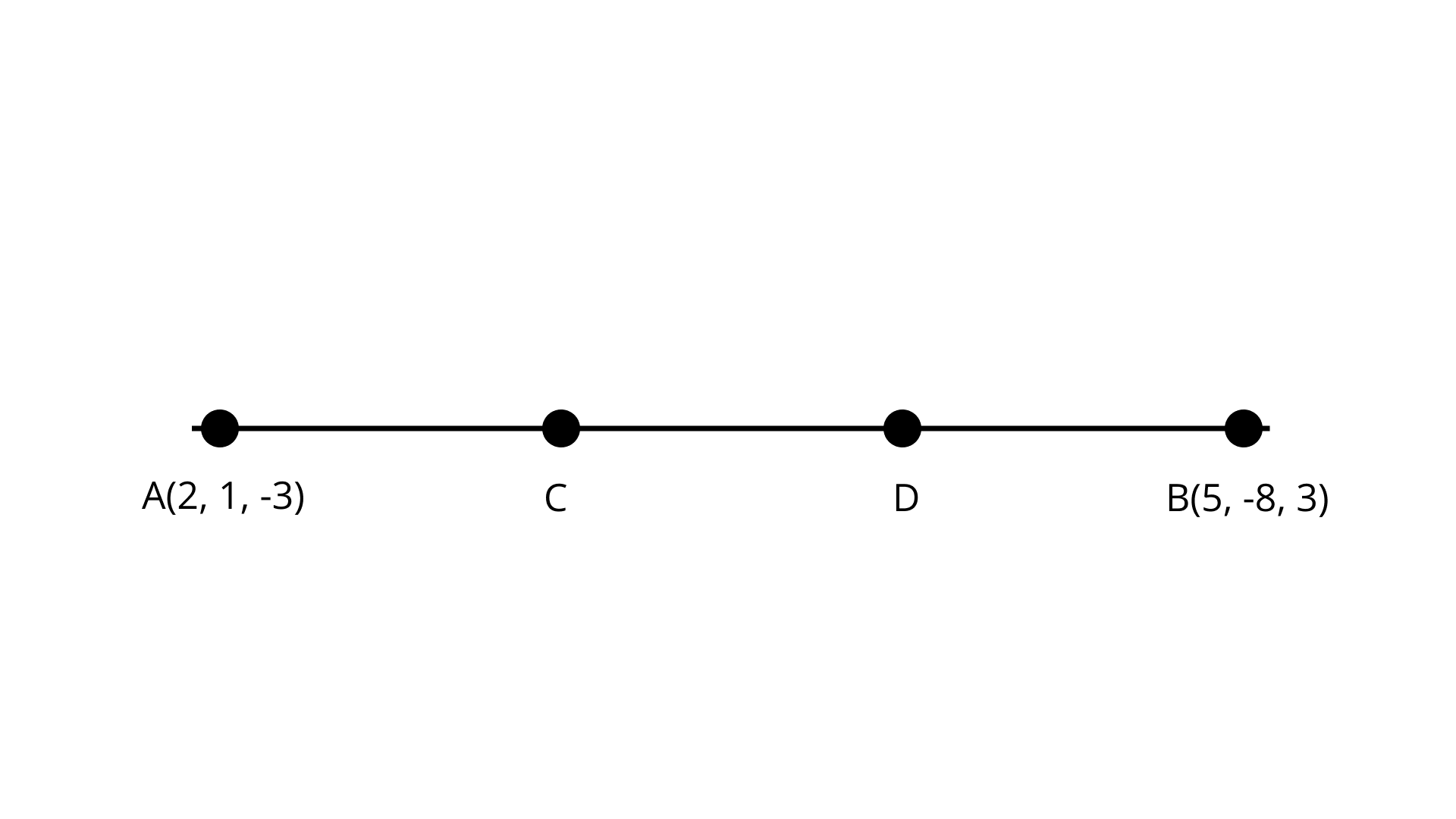
Ans: Given: The points ${\text{A}}\left( {2,1,-3} \right)$ and ${\text{B}}\left( {5,-8,3} \right)$.

Let ${\text{C}}$ and ${\text{D}}$be the points which divide the given line ${\text{AB}}$into three equal parts. 

Here ${\text{AC}}:{\text{CB}} = 1:2$

Let $\left( {{x_1},{y_1},{z_1}} \right)$be the coordinates of ${\text{C}}$ 

${x_1} = \dfrac{{1 \times 5 + 2 \times 2}}{{1 + 2}} = 3$

${y_1} = \dfrac{{1 \times  - 8 + 2 \times 1}}{{1 + 2}} =  - 2$

${z_1} = \dfrac{{1 \times 3 + 2 \times  - 3}}{{1 + 2}} =  - 1$

So $C = \left( {3, - 2, - 1} \right).$

Now ${\text{D}}$ is the midpoint $= CB$

Let the coordinates of ${\text{D}}$be $\left( {{x_2},{y_2},{z_2}} \right)$

${x_2} = \dfrac{{3 + 5}}{2} = 4$

${y_2} = \dfrac{{ - 8 - 2}}{2} =  - 5$

${z_2} = \dfrac{{3 - 1}}{2} = 1$

So, ${\text{D}} = (4, - 5,1)$

Hence, the required coordinates are ${\text{C}}(3, - 2, - 1)$ and ${\text{D}}(4, - 5,1).$

16. If the origin is the centroid of a triangle $ABC$ having vertices are $A\left( {a, 1, 3} \right)$, $B\left( { - 2, b,  - 5} \right)$ and $C\left( {4, 7, c} \right)$, find the values of $a$, $b$ and $c$.

Ans: Given: A triangle $ABC$ whose centroid is the origin.

The vertices of the triangle are $A\left( {a,{\text{ }}1,{\text{ }}3} \right)$, $B\left( { - 2,{\text{ }}b,{\text{ }} - 5} \right)$ and $C\left( {4,{\text{ }}7,{\text{ }}c} \right)$.

Use the formula for the coordinates of a centroid of a triangle given as $\left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},{\text{ }}\dfrac{{{y_1} + {y_2} + {y_3}}}{3},{\text{ }}\dfrac{{{z_1} + {z_2} + {z_3}}}{3}} \right)$. Here $\left( {{x_1},{\text{ }}{y_1},{\text{ }}{z_1}} \right)$, $\left( {{x_2},{\text{ }}{y_2},{\text{ }}{z_2}} \right)$ and $\left( {{x_3},{\text{ }}{y_3},{\text{ }}{z_3}} \right)$ are the vertices of the triangle.

Since the centroid of the triangle is the origin, so its coordinates is $\left( {0,{\text{ }}0,{\text{ }}0} \right)$. If a triangle has its vertices $\left( {{x_1},{\text{ }}{y_1},{\text{ }}{z_1}} \right)$, $\left( {{x_2},{\text{ }}{y_2},{\text{ }}{z_2}} \right)$ and $\left( {{x_3},{\text{ }}{y_3},{\text{ }}{z_3}} \right)$ then its centroid is $\left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},{\text{ }}\dfrac{{{y_1} + {y_2} + {y_3}}}{3},{\text{ }}\dfrac{{{z_1} + {z_2} + {z_3}}}{3}} \right)$.

$\Rightarrow \left( {\dfrac{{a + \left( { - 2} \right) + 4}}{3},{\text{ }}\dfrac{{1 + b + 7}}{3},{\text{ }}\dfrac{{3 + \left( { - 5} \right) + c}}{3}} \right) = \left( {0,{\text{ }}0,{\text{ }}0} \right)$

$\Rightarrow \left( {\dfrac{{a + 2}}{3},{\text{ }}\dfrac{{b + 8}}{3},{\text{ }}\dfrac{{c - 2}}{3}} \right) = \left( {0,{\text{ }}0,{\text{ }}0} \right)$ 

Equating the respective coordinates and solving,

$a =  - 2$, $b =  - 8$ and $c = 2$

17. Let $A\left( {2, 2,  - 3} \right)$, $B\left( {5, 6, 9} \right)$ and $C\left( {2, 7, 9} \right)$ be the vertices of a triangle. The internal bisector of the angle $A$ meets $BC$ at point $D$. Find the coordinates of point $D$.

Ans: Given: The vertices of the triangle are $A\left( {2,{\text{ }}2,{\text{ }} - 3} \right)$, $B\left( {5,{\text{ }}6,{\text{ }}9} \right)$ and $C\left( {2,{\text{ }}7,{\text{ }}9} \right)$. $AD$ is the internal bisector of angle $A$ and meets the side $BC$ at $D$. Assume the coordinates of $D$ as $\left( {x,{\text{ }}y,{\text{ }}z} \right)$. Use the angle bisector theorem given as $\dfrac{{AB}}{{AC}} = \dfrac{{BD}}{{DC}}$ and find the use the distance formula to find $AB$ and $AC$.

Now, use the section formula for the points $B$, $D$ and $C$. If $AD$ is the angle bisector of the angle $A$ and it meets $BC$ at $D$ then by the angle bisector theorem $\dfrac{{AB}}{{AC}} = \dfrac{{BD}}{{DC}}$.

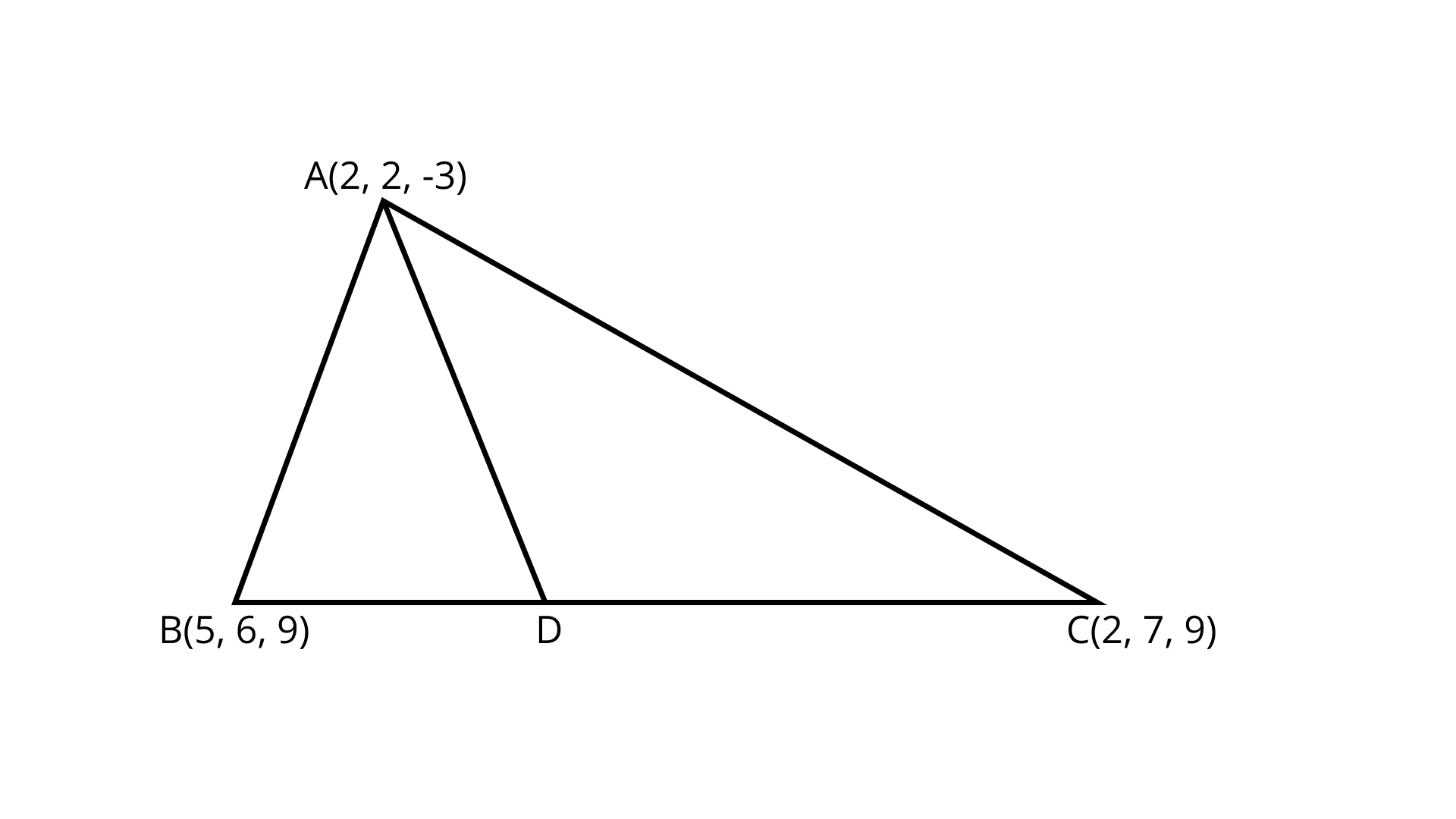
Using the distance formula the length of $AB$ 

$= \sqrt {{{\left( {5 - 2} \right)}^2} + {{\left( {6 - 2} \right)}^2} + {{\left( {9 - \left( { - 3} \right)} \right)}^2}}$

$= \sqrt {9 + 16 + 144}$

$= 13{\text{ units}}$ 

Similarly, the length of $AC$

$= \sqrt {{{\left( {2 - 2} \right)}^2} + {{\left( {7 - 2} \right)}^2} + {{\left( {9 - \left( { - 3} \right)} \right)}^2}}$

$= \sqrt {25 + 144}$

$= 13{\text{ units}}$ 

Therefore, the ratio $\dfrac{{BD}}{{DC}} = 1$ and so $BD = DC$. Clearly the point $D$ is the midpoint of $BC$. Using the midpoint formula for its coordinates,

$\Rightarrow \left( {x,{\text{ }}y,{\text{ }}z} \right) = \left( {\dfrac{{5 + 2}}{2},{\text{ }}\dfrac{{7 + 6}}{2},{\text{ }}\dfrac{{9 + 9}}{2}} \right)$

$\Rightarrow \left( {x,{\text{ }}y,{\text{ }}z} \right) = \left( {\dfrac{7}{2},{\text{ }}\dfrac{{13}}{2},{\text{ }}9} \right)$ 

18. Show that the three points $A\left( {2, 3, 4} \right)$, $B\left( { - 1, 2,  - 3} \right)$ and $C\left( { - 4, 1,  - 10} \right)$ are collinear and find the ratio in which $C$ divides $AB$.

Ans: Given: The points $A\left( {2,{\text{ }}3,{\text{ }}4} \right)$, $B\left( { - 1,{\text{ }}2,{\text{ }} - 3} \right)$ and $C\left( { - 4,{\text{ }}1,{\text{ }} - 10} \right)$.

Find the lengths $AB$, $BC$ and $AC$. Check if the sum of two distances is equal to the third distance. If yes then the points are collinear.

To find the required ratio use the section formula for the points $A$, $C$ and $B$. Using the distance formula, the length $AB$ is,

$\Rightarrow AB = \sqrt {{{\left( { - 1 - 2} \right)}^2} + {{\left( {2 - 3} \right)}^2} + {{\left( { - 3 - 4} \right)}^2}}$

$\Rightarrow AB = \sqrt {9 + 1 + 49}$

$\Rightarrow AB = \sqrt {59} {\text{ units}}$ 

Similarly, the length $BC$ is,

$\Rightarrow BC = \sqrt {{{\left( { - 4 - \left( { - 1} \right)} \right)}^2} + {{\left( {1 - 2} \right)}^2} + {{\left( { - 10 - \left( { - 3} \right)} \right)}^2}}$

$\Rightarrow BC = \sqrt {9 + 1 + 49}$

$\Rightarrow BC = \sqrt {59} {\text{ units}}$ 

Also, the length $AC$ is,

$\Rightarrow AC = \sqrt {{{\left( { - 4 - 2} \right)}^2} + {{\left( {1 - 3} \right)}^2} + {{\left( { - 10 - 4} \right)}^2}}$

$\Rightarrow AC = \sqrt {36 + 4 + 196}$

$\Rightarrow AC = 2\sqrt {59} {\text{ units}}$ 

Clearly $AB + BC = AC$, so the three points are collinear.

Now, let us assume the ratio in which $C$ divides $AC$ is $m:n$. Using the section formula for the $x$ coordinates of the points $A$, $C$ and $B$,

$\Rightarrow x$ coordinate of $C = \dfrac{{m \times \left( { - 1} \right) + n \times \left( 2 \right)}}{{m + n}}$

$\Rightarrow  - 4 = \dfrac{{ - m + 2n}}{{m + n}}$

$\Rightarrow  - 4m - 4n =  - m + 2n$

$\Rightarrow  - 3m = 6n$

$\Rightarrow \dfrac{m}{n} = \dfrac{{ - 2}}{1}$ 

Hence, $C$ divides $AB$ externally in the ratio $2:1$.

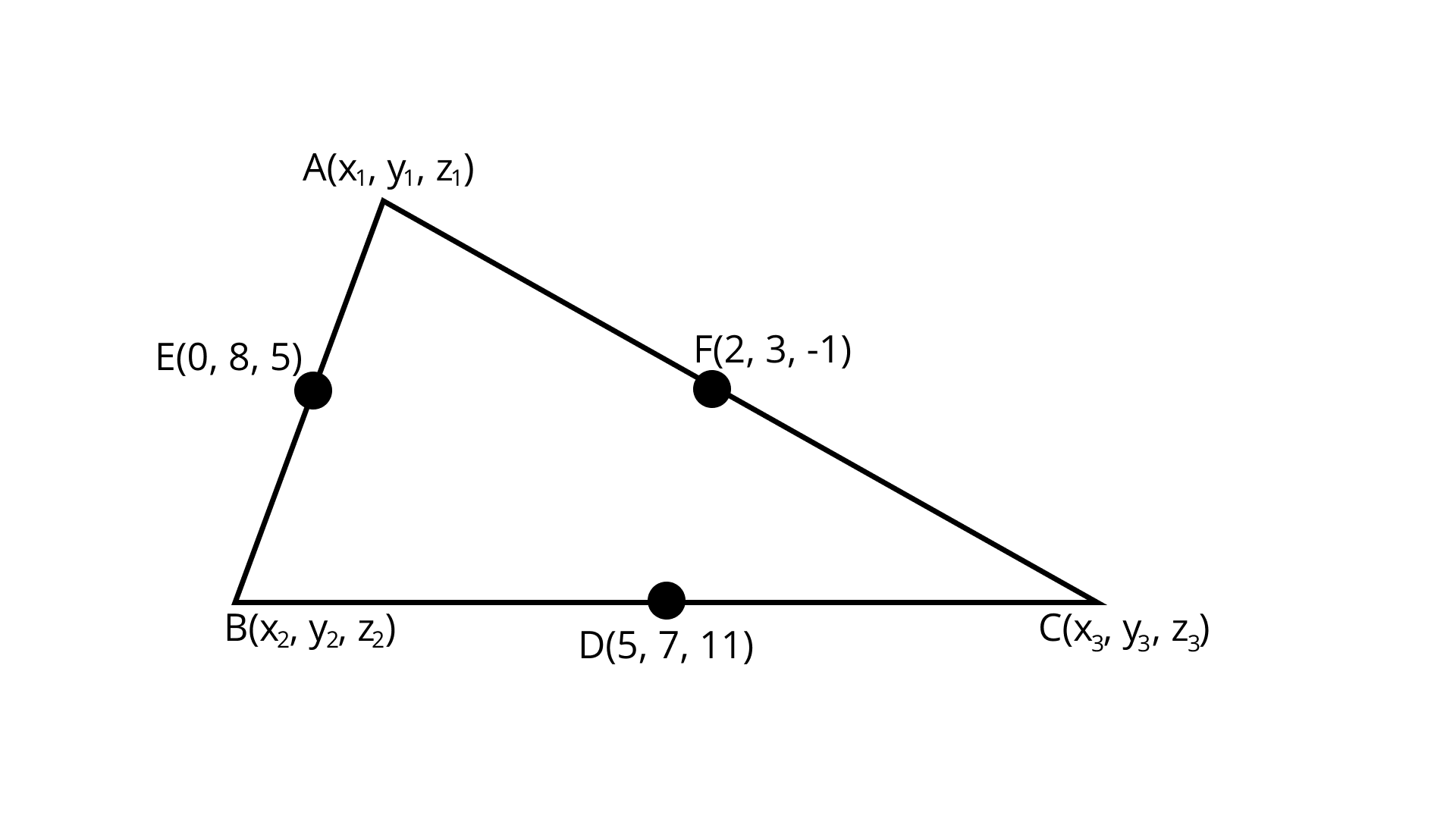
19. The mid-points of the sides of a triangle are $\left( {1, 5,  - 1} \right)$, $\left( {0, 4,  - 2} \right)$ and $\left( {2, 3, 4} \right)$. Find its vertices. Also find the centroid of the triangle.

Ans: Given: The mid-points of the sides of a triangle are $\left( {1,{\text{ }}5,{\text{ }} - 1} \right)$, $\left( {0,{\text{ }}4,{\text{ }} - 2} \right)$ and $\left( {2,{\text{ }}3,{\text{ }}4} \right)$

Assume $\left( {{x_1},{\text{ }}{y_1},{\text{ }}{z_1}} \right)$, $\left( {{x_2},{\text{ }}{y_2},{\text{ }}{z_2}} \right)$ and $\left( {{x_3},{\text{ }}{y_3},{\text{ }}{z_3}} \right)$ as the vertices of the triangle.

Use the midpoint formula to form the relations between the coordinates of the mid-points and the vertices.

To find the centroid use the formula $\left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},{\text{ }}\dfrac{{{y_1} + {y_2} + {y_3}}}{3},{\text{ }}\dfrac{{{z_1} + {z_2} + {z_3}}}{3}} \right)$.

Let us assume the vertices of the triangle are $A\left( {{x_1},{\text{ }}{y_1},{\text{ }}{z_1}} \right)$, $B\left( {{x_2},{\text{ }}{y_2},{\text{ }}{z_2}} \right)$ and $C\left( {{x_3},{\text{ }}{y_3},{\text{ }}{z_3}} \right)$ whereas the mid-points of the sides $AB$, $BC$ and $CA$ are $D\left( {1,{\text{ }}5,{\text{ }} - 1} \right)$, $E\left( {0,{\text{ }}4,{\text{ }} - 2} \right)$ and $F\left( {2,{\text{ }}3,{\text{ }}4} \right)$ respectively.

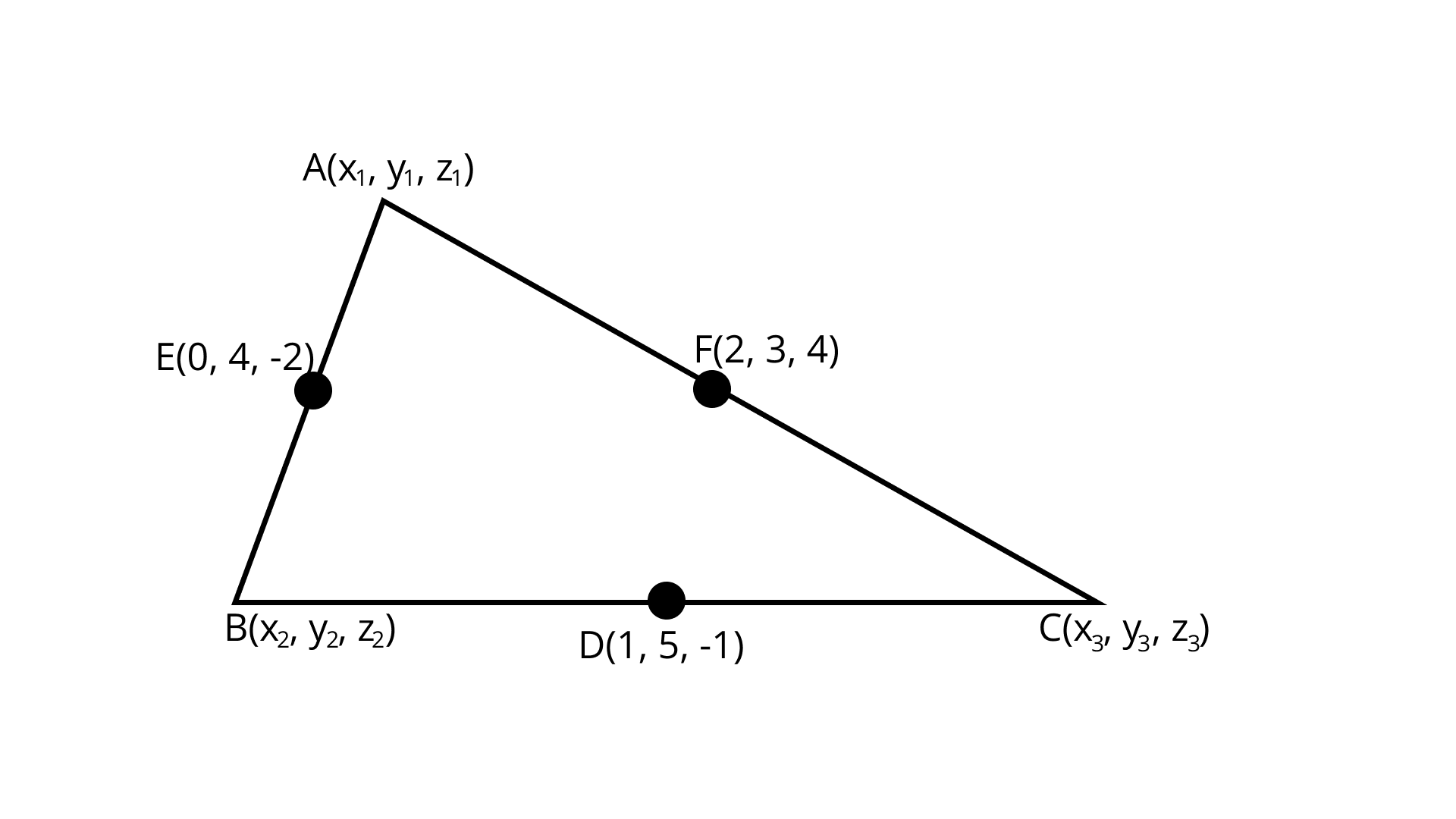
Using the midpoint formula for the $x$ coordinates, 

$x$ coordinate of $D = \dfrac{{{x_1} + {x_2}}}{2}$

$\Rightarrow 1 = \dfrac{{{x_1} + {x_2}}}{2}$ … (i)

$x$ coordinate of $E = \dfrac{{{x_2} + {x_3}}}{2}$

$\Rightarrow 0 = \dfrac{{{x_2} + {x_3}}}{2}$ … (ii)

$x$ coordinate of $F = \dfrac{{{x_3} + {x_1}}}{2}$

$\Rightarrow 2 = \dfrac{{{x_3} + {x_1}}}{2}$ … (iii)

Solving the three equations gives ${x_1} = 3$, ${x_2} =  - 1$ and ${x_3} = 1$.

Similarly for the $y$ coordinates,

$y$ coordinate of $D = \dfrac{{{y_1} + {y_2}}}{2}$

$\Rightarrow 5 = \dfrac{{{y_1} + {y_2}}}{2}$ … (i)

$y$ coordinate of $E = \dfrac{{{y_2} + {y_3}}}{2}$

$\Rightarrow 4 = \dfrac{{{y_2} + {y_3}}}{2}$ … (ii)

$y$ coordinate of $F = \dfrac{{{y_3} + {y_1}}}{2}$

$\Rightarrow 3 = \dfrac{{{y_3} + {y_1}}}{2}$ … (iii)

Solving the three equations gives ${y_1} = 4$, ${y_2} = 6$ and ${y_3} = 2$.

Finally, for the $z$ coordinates,

$z$ coordinate of $D = \dfrac{{{z_1} + {z_2}}}{2}$

$\Rightarrow  - 1 = \dfrac{{{z_1} + {z_2}}}{2}$ … (i)

$z$ coordinate of $E = \dfrac{{{z_2} + {z_3}}}{2}$

$\Rightarrow  - 2 = \dfrac{{{z_2} + {z_3}}}{2}$ … (ii)

$z$ coordinate of $F = \dfrac{{{z_3} + {z_1}}}{2}$

$\Rightarrow 4 = \dfrac{{{z_3} + {z_1}}}{2}$ … (iii)

Solving the three equations gives ${z_1} = 5$, ${z_2} =  - 7$ and ${z_3} = 3$.

Therefore, the vertices of the triangle are $A\left( {3,{\text{ }}4,{\text{ }}5} \right)$, $B\left( { - 1,{\text{ }}6,{\text{ }} - 7} \right)$ and $C\left( {1,{\text{ }}2,{\text{ }}3} \right)$.

Now, the centroid of the triangle is

$= \left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},{\text{ }}\dfrac{{{y_1} + {y_2} + {y_3}}}{3},{\text{ }}\dfrac{{{z_1} + {z_2} + {z_3}}}{3}} \right)$

$= \left( {\dfrac{{3 + \left( { - 1} \right) + 1}}{3},{\text{ }}\dfrac{{4 + 6 + 2}}{3},{\text{ }}\dfrac{{5 + \left( { - 7} \right) + 3}}{3}} \right)$

$= \left( {1,{\text{ }}4,{\text{ }}\dfrac{1}{3}} \right)$ 

20. Prove that the points $\left( {0,  - 1,  - 7} \right)$, $\left( {2, 1,  - 9} \right)$ and $\left( {6, 5,  - 13} \right)$ are collinear. Find the ratio in which the first point divides the join of the two points.

Ans: Given: The points $\left( {0,{\text{ }} - 1,{\text{ }} - 7} \right)$, $\left( {2,{\text{ }}1,{\text{ }} - 9} \right)$ and $\left( {6,{\text{ }}5,{\text{ }} - 13} \right)$.

Assume the points as $A$, $B$ and $C$ respectively. Find the lengths $AB$, $BC$ and $AC$. Check if the sum of two distances is equal to the third distance. If yes then the points are collinear. To find the required ratio use the section formula for the points $B$, $A$ and $C$.

Using the distance formula, the length $AB$ is,

$\Rightarrow AB = \sqrt {{{\left( {2 - 0} \right)}^2} + {{\left( {1 - \left( { - 1} \right)} \right)}^2} + {{\left( { - 9 - \left( { - 7} \right)} \right)}^2}}$

$\Rightarrow AB = \sqrt {4 + 4 + 4}$

$\Rightarrow AB = 2\sqrt 3 {\text{ units}}$ 

Similarly, the length $BC$ is,

$\Rightarrow BC = \sqrt {{{\left( {6 - 2} \right)}^2} + {{\left( {5 - 1} \right)}^2} + {{\left( { - 13 - \left( { - 9} \right)} \right)}^2}}$

$\Rightarrow BC = \sqrt {16 + 16 + 16}$

$\Rightarrow BC = 4\sqrt 3 {\text{ units}}$ 

Also, the length $AC$ is,

$\Rightarrow AC = \sqrt {{{\left( {6 - 0} \right)}^2} + {{\left( {5 - \left( { - 1} \right)} \right)}^2} + {{\left( { - 13 - \left( { - 7} \right)} \right)}^2}}$

$\Rightarrow AC = \sqrt {36 + 36 + 36}$

$\Rightarrow AC = 6\sqrt 3 {\text{ units}}$ 

Clearly $AB + BC = AC$, so the three points are collinear.

Now, let us assume the ratio in which the first point $A$ divides $BC$ is $m:n$. Using the section formula for the $x$ coordinates of the points $B$, $A$ and $C$,

$\Rightarrow x$ coordinate of $A = \dfrac{{m \times 6 + n \times 2}}{{m + n}}$

$\Rightarrow 0 = \dfrac{{6m + 2n}}{{m + n}}$

$\Rightarrow 0 = 6m + 2n$

$\Rightarrow 6m =  - 2n$

$\Rightarrow \dfrac{m}{n} = \dfrac{{ - 1}}{3}$ 

Hence, $A$ divides $BC$ externally in the ratio $1:3$.

21. What are the coordinates of the vertices of a cube whose edge is $2\, units$, one of whose vertices coincides with the origin and the three edges passing through the origin, coincides with the positive direction of the axes through the origin?

Ans: Given: Edge length of the cube $= 2{\text{ units}}$

One of the vertices coincides with the origin.

Three edges passing through the origin coincides with the positive direction of the axes.

Draw a diagram of the cube according to the conditions given. Start from the origin and use the sign convention of the coordinates in a specific quadrant to find the vertices.

The diagram of the cube according to the given conditions can be shown below: -

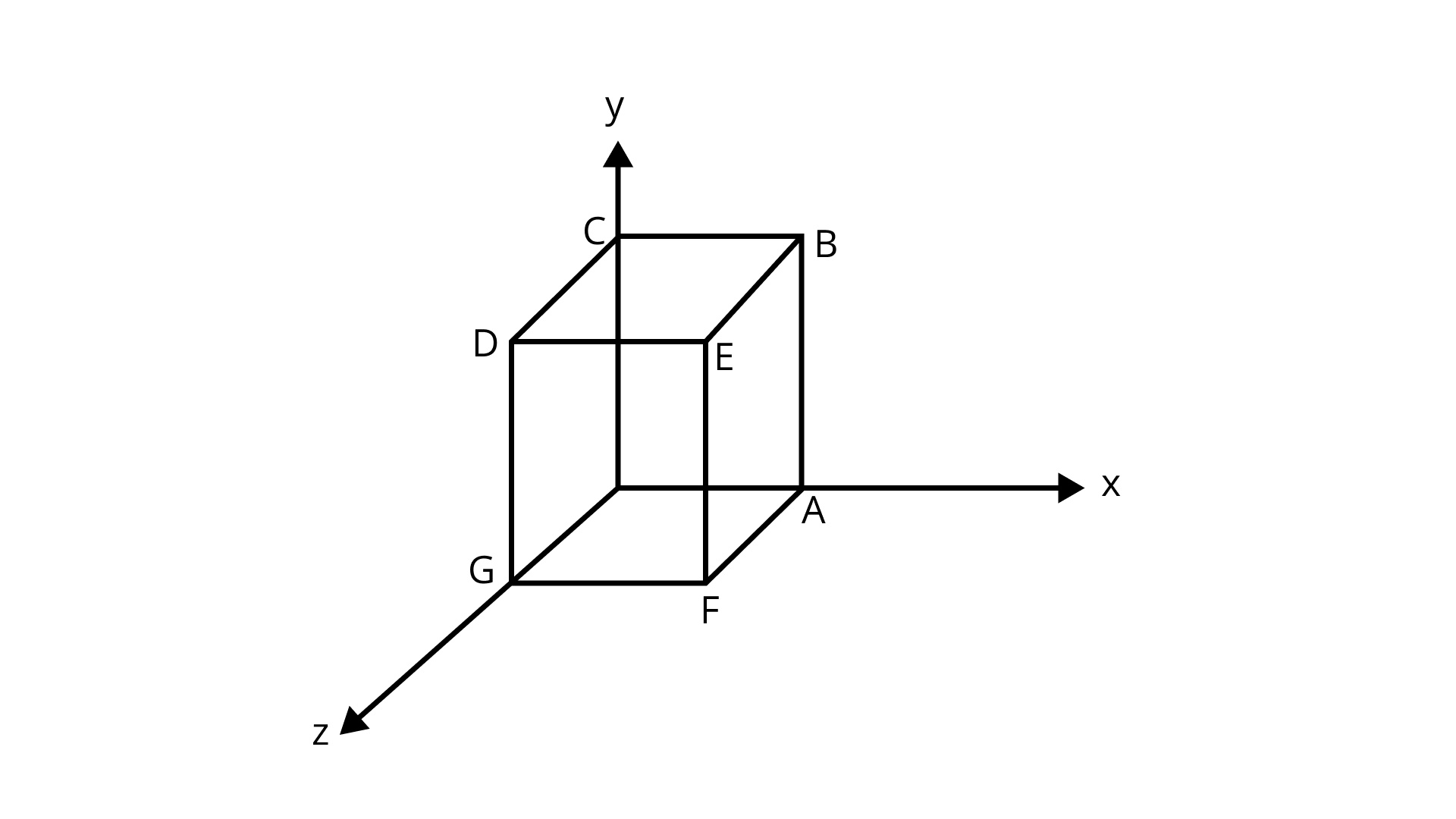
Here one of the vertices is the origin $O$, so its coordinate is $\left( {0,{\text{ }}0,{\text{ }}0} \right)$.

Since point $A$ lies on the $x$ axis so its coordinate is $\left( {2,{\text{ }}0,{\text{ }}0} \right)$.

Point $C$ lies on the $y$ axis so its coordinate is $\left( {0,{\text{ }}2,{\text{ }}0} \right)$.

Point $G$ lies on the $z$ axis so its coordinate is $\left( {0,{\text{ }}0,{\text{ }}2} \right)$.

Since point $B$ lies in the $xy$ plane so its coordinate is $\left( {2,{\text{ }}2,{\text{ }}0} \right)$.

Point $D$ lies in the $yz$ plane so its coordinate is $\left( {0,{\text{ }}2,{\text{ }}2} \right)$.

Point $F$ lies in the $xz$ plane so its coordinate is $\left( {2,{\text{ }}0,{\text{ }}2} \right)$.

Now, the point $E$ lies in the $3 - D$ space so its coordinate is $\left( {2,{\text{ }}2,{\text{ }}2} \right)$.

22. The distance of point $P\left( {3, 4, 5} \right)$ from the $yz$ plane is

(a) 3 units

(b) 4 units

(c) 5 units

(d) 550 units

Ans: Option (c)

Given:The point $P\left( {3,{\text{ }}4,{\text{ }}5} \right)$.

Use the fact that the distance of a point $P\left( {{x_1},{\text{ }}{y_1},{\text{ }}{z_1}} \right)$ from the $yz$ plane is its $x$ coordinate.

The distance of a point $P\left( {{x_1},{\text{ }}{y_1},{\text{ }}{z_1}} \right)$ from the $yz$ plane is its $x$ coordinate ${x_1}$.

Therefore, the distance of the point $P\left( {3,{\text{ }}4,{\text{ }}5} \right)$ from the $yz$ plane $= 3{\text{ units}}$.

23. What is the length of the perpendicular foot drawn from the point $P\left( {3, 4, 5} \right)$ on $y$ axis?

(a) \[\sqrt {41}\]

(b) \[\sqrt {34}\]

(c) 5

(d) None of these

Ans: Option (b)

Given: The point $P\left( {3,{\text{ }}4,{\text{ }}5} \right)$.

The length of foot of perpendicular from a point $P\left( {{x_1},{\text{ }}{y_1},{\text{ }}{z_1}} \right)$ on the $y$ axis is $\sqrt {{x_1}^2 + {z_1}^2}$.

Therefore, the length of foot of perpendicular from the point $P\left( {3,{\text{ }}4,{\text{ }}5} \right)$ on the $y$ axis

$= \sqrt {{3^2} + {5^2}}$

$= \sqrt {34}$ 

24. Distance of the point $\left( {3, 4, 5} \right)$ from the origin is

(a) \[\sqrt {50}\]

(b) 3

(c) 4

(d) 5

Ans: Option (a)

Given:The origin and the point $\left( {3,{\text{ }}4,{\text{ }}5} \right)$.

Use the formula of the distance between the two points $\left( {{x_1},{\text{ }}{y_1},{\text{ }}{z_1}} \right)$ and $\left( {{x_2},{\text{ }}{y_2},{\text{ }}{z_2}} \right)$ given as $\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}}$.

The origin is given by the coordinates $\left( {0,{\text{ }}0,{\text{ }}0} \right)$. Let us assume the distance between the points $\left( {0,{\text{ }}0,{\text{ }}0} \right)$ and $\left( {3,{\text{ }}4,{\text{ }}5} \right)$ is $d$.

The distance between the two points having coordinates $\left( {{x_1},{\text{ }}{y_1},{\text{ }}{z_1}} \right)$ and $\left( {{x_2},{\text{ }}{y_2},{\text{ }}{z_2}} \right)$ is given as $\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}}$.

$\Rightarrow d = \sqrt {{{\left( {3 - 0} \right)}^2} + {{\left( {4 - 0} \right)}^2} + {{\left( {5 - 0} \right)}^2}}$

$\Rightarrow d = \sqrt {9 + 16 + 25}$

$\Rightarrow d = \sqrt {50}$ 

25. If the distance between the points $\left( {a,{\text{ }}0,{\text{ }}1} \right)$ and $\left( {0,{\text{ }}1,{\text{ }}2} \right)$ is $\sqrt {27}$, then the value of $a$ is

(a) 5

(b) \[\pm 5\]

(c) - 5

(d) None of these

Ans: Option (b)

Given: The points $\left( {a,{\text{ }}0,{\text{ }}1} \right)$ and $\left( {0,{\text{ }}1,{\text{ }}2} \right)$.

Distance between the two points $= \sqrt {27}$

The distance between the two points having coordinates $\left( {{x_1},{\text{ }}{y_1},{\text{ }}{z_1}} \right)$ and $\left( {{x_2},{\text{ }}{y_2},{\text{ }}{z_2}} \right)$ is given as $\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}}$. Therefore, for the points $\left( {a,{\text{ }}0,{\text{ }}1} \right)$ and $\left( {0,{\text{ }}1,{\text{ }}2} \right)$,

$\Rightarrow d = \sqrt {27}$

$\Rightarrow \sqrt {{{\left( {0 - a} \right)}^2} + {{\left( {1 - 0} \right)}^2} + {{\left( {2 - 1} \right)}^2}}  = \sqrt {27}$

$\Rightarrow {a^2} + 2 = 27$

$\Rightarrow{a^2} = 25$ 

Taking square root both the sides,

$\Rightarrow a =  \pm 5$

26. $x -$ axis is the intersection of two planes
(a) xy and xz                                           
(b) yz and zx
(c) xy and yz                                           
(d) none of these

Ans: Option (a)

Given: $x -$ axis is the intersection of two planes.

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

On the $xy$ and $xz$ planes , the line of intersection is the $x -$ axis.

Hence, the two planes are $xy$ and $xz$.

27. Equation of $y$ - axis is considered as
(a) x = 0, y = 0                                          
(b) y = 0, z = 0
(c) z = 0, x = 0
(d) none of these

Ans: Option (c)

Given: $y -$ axis.

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

On the $y -$ axis: $z = 0$, $x = 0$

Hence $z = 0$, $x = 0$.

28.The point $( - 2, - 3, - 4)$ lies  in the

(a) First octant                                           
(b) Seventh octant  
(c) Second octant  
(d) Eighth octant  

Ans: Option (b)

Given: $( - 2, - 3, - 4)$

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

$( - 2, - 3, - 4)$ lies in the seventh octant.

Hence seventh octant is the correct answer.

29.A plane is parallel to $yz -$ plane so it is perpendicular to

(a) x - axis
(b) y - axis
(c) z - axis
(d) none of these 

Ans: Option (a)

Given: A plane is parallel to $yz -$ plane.

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

As the plane is parallel to $yz -$ plane, it is perpendicular to $x -$ axis.

Hence, the plane is perpendicular to $x -$ axis.

30. The locus of a point for which $y = 0$, $z = 0$ is

(a) equation of $x -$ axis
(b) equation of $y -$ axis
(c) equation of $z -$ axis
(d) none of these 

Ans: Option (a)

Given: $y = 0$, $z = 0$.

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

$y = 0$, $z = 0$ is the equation of $x -$ axis.

Hence, the locus is the equation of $x -$ axis.

31. The locus of a point for which $x = 0$ is

(a) xy - plane
(b) yz - plane
(c) zx - plane
(d) none of these

Ans: Option (b)

Given: $x = 0$.

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

$x = 0$ on the $yz -$ plane.
Hence, the locus is $yz -$ plane.

32.If a parallelepiped is formed by planes drawn through the points $(5,8,10)$ and $(3,6,8)$ parallel to the coordinate planes, then the length of diagonal of the parallelepiped is 

(a) \[2\sqrt 3\]
(b) \[3\sqrt 2\]
(c) \[\sqrt 2\]
(d) \[\sqrt 3\]

Ans: Option (a)

Given: $(5,8,10)$ and $(3,6,8)$.

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

The length of diagonal is:

$\Rightarrow AB = \sqrt {{{(5 - 3)}^2} + {{(8 - 6)}^2} + {{(10 - 8)}^2}}$

$\Rightarrow AB = \sqrt {4 + 4 + 4}$

$\Rightarrow AB = 2\sqrt 3$

Hence, the length of diagonal of the parallelepiped is $2\sqrt 3 .$

33. $L$ is the foot of the perpendicular drawn from a point $P(3,4,5)$ on the $xy -$ plane. The coordinates of point $L$ are

(a) (3,0,0)
(b) (0,4,5)
(c) (3,0,5)
(d) none of these

Ans: Option (d)

Given: $P(3,4,5)$.

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

On the $xy -$ plane, $z = 0$.

Hence, the coordinates of point $L$ are $(3,4,0)$.

34. $L$ is the foot of the perpendicular drawn from a point $(3,4,5)$ on $x -$ axis. The coordinates of $L$ are

(a) (3,0,0)
(b) (0,4,0)
(c) (0,0,5)
(d) none of these

Ans: Option (a)

Given: $(3,4,5)$.

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

On the $x -$ axis, $y = 0$ and $z = 0$.

Hence, the coordinates of $L$ are $(3,0,0)$.

35. The three axes $OX,$$OY,$$OZ$ determine.

Ans: Given: $OX,$$OY,$$OZ$

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

The three axes $OX,$$OY,$$OZ$ determine $3$ coordinate planes.

Hence, $OX,$$OY,$$OZ$ determine $3$ coordinate planes.

36. The three planes determine a rectangular parallelepiped which has $\_\_\_\_\_\_\_\_$of rectangular faces.

Ans: Given: The three planes determine a rectangular parallelepiped.

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

The rectangular parallelepiped determined by three planes has three pairs of rectangular faces.

Hence, the rectangular parallelepiped has three pairs of rectangular faces.

37. The coordinates of a point are the perpendicular distance from the $\_\_\_\_\_\_\_\_$ on the respective axes.

Ans: Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

The coordinates of a point are the perpendicular distance from the given points on the respective axes.

38. The three coordinate planes divide the space into$\_\_\_\_\_\_\_\_$parts.

Ans: Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

The three coordinate planes divide the space into $8$ parts.

Hence, the space is divided into $8$ parts.

39. If a point $P$ lies  on $yz -$ plane, then the coordinates of a point on $yz -$ plane is of the form __________.

Ans: Given: $P$ lies  on $yz -$ plane.

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

On the $yz -$ plane, $x = 0$. 

Hence, the coordinates are of the form $(0,y,z)$.

40. The equation of $yz -$ plane is __________.

Ans: Given: $yz -$ plane.

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

For any point on the $yz -$ plane, the $x -$ coordinate is $0$. 

Hence, the equation of$yz -$ plane is $x = 0$.

41. If the point $P$ lies  on $z -$ axis, then coordinates of $P$ are of the form _________.

Ans: Given: $P$ lies  on $z -$ axis.

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

On the $z -$ axis, $x = 0$ and $y = 0$.

Hence, the coordinates are of the form $(0,0,z)$.

42. The equations of $z -$ axis are __________.

Ans: Given: $z -$ axis 

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

On the $z -$ axis, the coordinates of any point are of the form $(0,0,z)$.

Hence, the equation of$z -$ axis is $x = 0$ and $y = 0$.

43. A line is parallel to $xy -$ plane if all the points on the line have equal _________.

Ans: Given: A line is parallel to $xy -$ plane. Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

A line is parallel to $xy -$ plane if every point on it is at the same distance from the $xy -$ plane.

The distance of any point from $xy -$ plane is $z$. Hence, all the points on the line have equal $z -$ coordinate. 

44. A line is parallel to $x -$ axis if all the points on the line have equal __________.

Ans: Given: A line is parallel to $x -$ axis.

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

A line is parallel to $x -$ axis if every point on it maintains a constant distance from$y -$ axis and $z -$ axis.

Hence, all the points on the line have equal $y$ and $z -$ coordinates.

45. $x = a$ represents a plane parallel to _________.

Ans: Given: $x = a$

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

The locus of a point $P(x,y,z)$ is $x = a$.

Every point $P$ has a constant $x -$ coordinate.

$x$ is the distance of $P$ from the $yz -$ plane. The plane $x = a$ is at constant distance $a$ from the $yz -$ plane.

Hence, $x = a$ represents a plane parallel to the$yz -$ plane.

46. The plane parallel to $yz -$ plane is perpendicular to __________.

Ans: Given: $yz -$ plane.

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

The plane parallel to $yz -$ plane is perpendicular to the $x -$ axis.

Hence, the plane which is parallel to $yz -$ plane is perpendicular to the $x -$ axis.

47. The length of the longest piece of a string that can be stretched straight in a rectangular room whose dimensions are $10,13$ and $8$ units are _________.

Ans: Given: Dimensions of rectangular rooms are $10,$$13$ and $8$ units.

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

Given dimensions are $a = 10,$$b = 13$ and $c = 8$.

The length of string required$= \sqrt {\left( {{a^2} + {b^2} + {c^2}} \right)}$

Required length $= \sqrt {\left( {{{10}^2} + {{13}^2} + {8^2}} \right)}$

Required length $= \sqrt {\left( {100 + 169 + 64} \right)}$

Required length $= \sqrt {333}$

Hence, the length of the longest piece of a string is $\sqrt {333}$.

48. If the distance between the points $(a,2,1)$ and $(1, - 1,1)$ is $5$, then $a$ ________.

Ans: Given: The distance between $(a,2,1)$ and $(1, - 1,1)$ is $5$.

Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

Given points are $(a,2,1)$ and $(1, - 1,1)$.

Given $\sqrt {{{\left( {a - 1} \right)}^2} + {{\left( {2 + 1} \right)}^2} + {{\left( {1 - 1} \right)}^2}}  = 5$

$\Rightarrow {\left( {a - 1} \right)^2} + 9 + 0 = 25$

$\Rightarrow {a^2} - 2a - 15 = 0$

$\Rightarrow \left( {a - 5} \right)\left( {a + 3} \right) = 0$

$\Rightarrow a = 5$ or $- 3$

Hence, $a = 5$ or $- 3$.

49. If the mid-points of the sides of a triangle $AB;$$BC;$$CA;$ are $D(1,2, - 3)$, $E(3,0,1)$ and $F( - 1,1, - 4)$, then the centroid of the triangle $ABC$ is ________.

Ans: Given: The mid-points of the sides of a triangle$AB;$$BC;$$CA;$ are$D(1,2, - 3)$, $E(3,0,1)$ and $F( - 1,1, - 4)$.

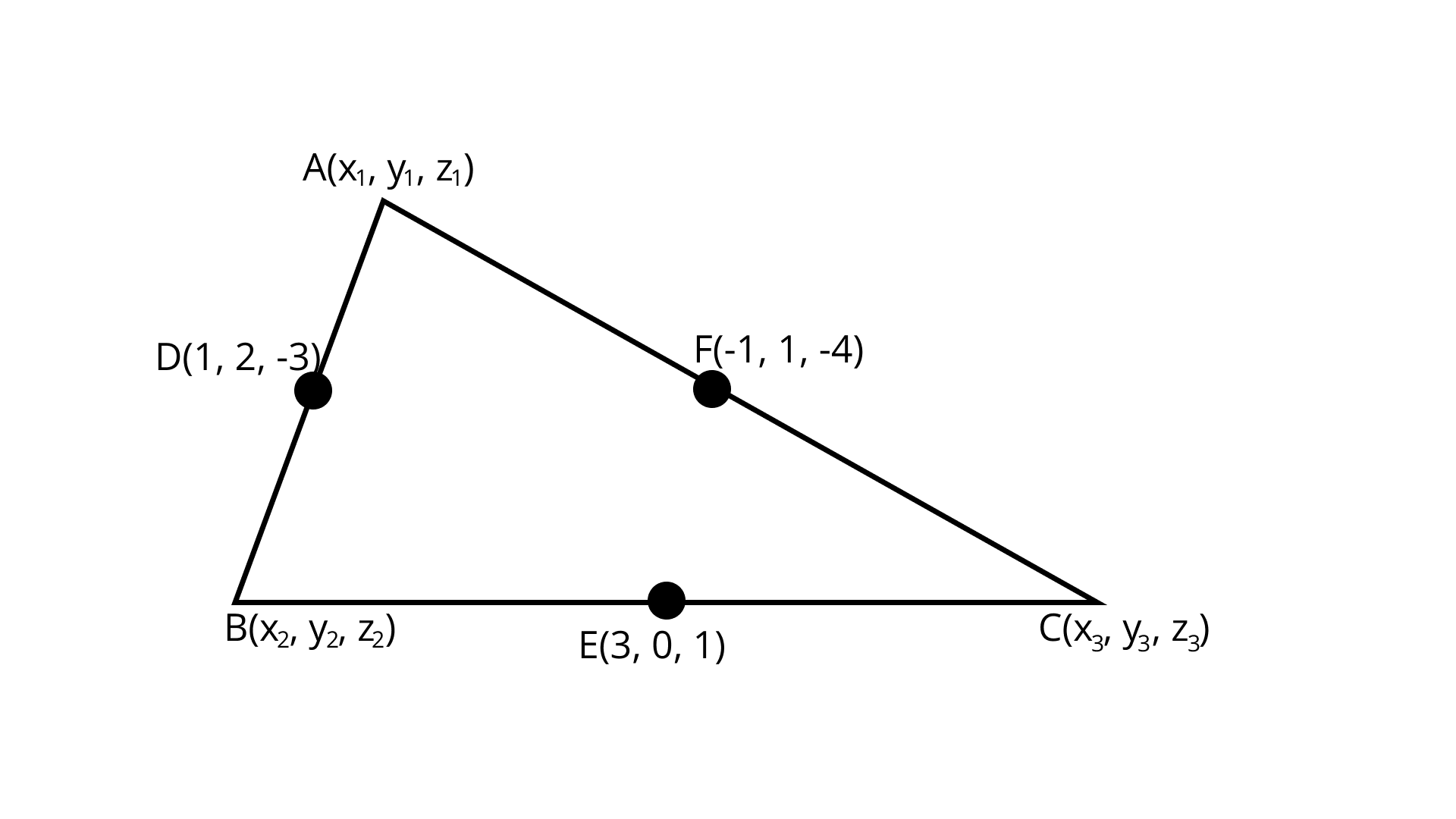
Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

Given that the mid-points of the sides of$\Delta ABC$ are $D(1,2, - 3)$, $E(3,0,1)$ and $F( - 1,1, - 4)$.

The centroid of the triangle formed by the midpoints of the sides of a triangle is the same as the centroid of the triangle.

So, the centroid of $\Delta DEF$ and the centroid of $\Delta ABC$ are the same.

Centroid of $\Delta ABC = G\left( {\dfrac{{1 + 3 - 1}}{3},\dfrac{{2 + 0 + 1}}{3},\dfrac{{ - 3 + 1 - 4}}{3}} \right)$

Centroid of $\Delta ABC = G\left( {1,1, - 2} \right)$

Hence, the centroid of the triangle is $\left( {1,1, - 2} \right)$.

50. Match each item given under the column ${C_1}$ to its correct answer given under column ${C_2}$.

Ans: Three dimensional geometry involves the mathematics of shapes in $3D$ space and the three coordinates in $XYZ$ plane.

(a) In $xy -$ plane, $z -$ coordinate is zero.

(b) The point $(2,3,4)$ lies in ${\text{I}}$st octant.

(c) Locus of the points having $x -$ coordinate zero is $yz -$ plane.

(d) A line is parallel to $x -$ axis if and only if all the points on the line have equal $y$ and $z -$ coordinates.

(e)$x = 0$, $y = 0$ represent $z -$ axis.

(f)$z = c$ represents the plane parallel to $xy -$ plane.

(g) The plane $x = a$ is parallel to $yz -$ plane.

The plane $y = b$ is parallel to $xz -$ plane.

The planes $x = a$ and $y = b$ is the line of intersection of these planes. 

The line of intersection of $yz -$ plane and $xz -$ plane is $z -$ axis.

Thus, the line of intersection of planes $x = a$ and $y = b$ is a line parallel to $z -$ axis.

(h) The coordinates of a point are the distances from the origin to the feet of perpendicular from the point on the respective axis.

(i) A ball is the solid region in the space enclosed by a sphere.

(j) The region in the plane enclosed by a circle is known as a disc. 

Hence,${\text{(a) - (iii), (b) - (i), (c) - (ii), (d) - (vi), (e) - (iv), (f) - (v), (g) - (viii), (h) - (vii), (i) - (x), (j) - (ix)}}$.

About NCERT

NCERT Exemplar for Class 11 chapter 12 deals with the Introduction to Three Dimensional Geometry. It involves the vector-algebra approach towards three-dimensional geometry with minimal use of complicated three-dimensional diagrams like triangles, etc. This chapter also explains the standard properties of lines and planes as well as three-dimensional space.

Three Dimensional Geometry includes three coordinates- x, y and z. They are mainly used to find the exact location of a point on a plane. The three coordinates are together known as the three-dimensional space. The three coordinate axes are then paired together- xy, yz, and zx which form three coordinate planes. We also discuss here the coordinates of a point in three-dimensional space as arbitrary point P is marked as (x0y0z0). These space coordinates are called Cartesian coordinates of P or rectangular coordinates of P. Next in line, we talk about the signs of coordinates of a point in which the sign depends on the octant in which the point lies. For example, in the first octant, all coordinates are positive and by the seventh octant, all the coordinates turn negative. In the fourth octant, x and z are positive while y is negative and in the sixth octant, it is the opposite, i.e., x and z are negative and y is positive. There are two formulas included in this chapter: 

• The Distance Formula between two points (A, B)= √(x2-x1)2+(y2-y1)2+(z2-z1)2 which is also the length of the diagonal.

• The Section Formula where the coordinates of point R that divides a line segment joining points P(x1, y1, z1) and Q(x2, y2, z2) in the ratio m:n is calculated as [(mx2+nx1)/(m+n)]+[(my2+ny1)/(m+n)]+[(mz2+nz1)/(m+n)], [(mx2-nx1)/(m-n)]+[(my2-ny1)/(m-n)]+[(mz2-nz1)/(m-n)]