Question

The longest chord of a circle is called its
A. Radius
B. Secant
C. Diameter
D. Tangent

Answer 1

Hint-In order to solve such a type of question, we will use the definition of radius of a circle that is defined as the distance from the center to the circumference of a circle.

“Complete step-by-step answer:”
Let AB be a diameter of the circle with center C and DE be chord away from C. Then, by the definition of the circle as the locus of points equidistant from the center,
CA=CB=CD=CE=R, the radius of the circle.

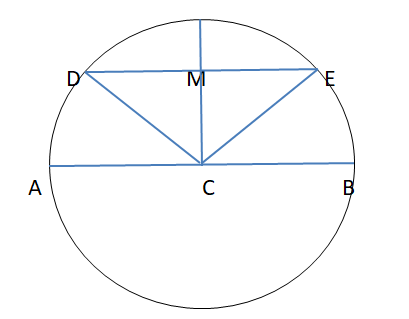
Which makes AB=2R. (The diameter is twice as long as the radius.)
On the other hand, in CDE, by the triangle inequality,
As we know, sum of two sides of triangle is greater than the third side
$ {\text{CD + CE > DE}} \\
  {\text{R + R > DE}} \\
  2{\text{R > DE}} \\
  {\text{AB >DE [}}\because {\text{AB = 2R]}} \\
 $
Hence, Diameter is the longest chord.
So, option C is the correct option.
Note- To solve these types of questions, you have to remember basic properties of triangles and circles. Such as Equal arc subtend equal angles and vice versa. Equal angles stand on equal chords and vice versa. Perpendicular bisector of a chord passes through the center of the circle. Sum of two sides of the triangle is greater than the third side.