Mechanical Properties of Fluids Class 11 Important Questions NEET Physics (PDF)

1. Choose which of the following is Pascal’s Law?

(A) There is an equal and opposite reaction to every action.

(B) The time rate of momentum change is defined as force.

(C) Pressure is directly proportional to temperature and constant volume and mass in an ideal gas.

(D) Any pressure change in the fluid is transferred throughout the fluid, causing the identical change to occur everywhere.

2. The operation of hydraulic machines is dependent on which of the following?

(A) Pascal’s Law

(B) Newton’s Law of Cooling

(C) Law of Gravitation

(D) Ideal Gas Law

3. What instrument is used to measure pressure?

(A) Odometer

(B) Barometer

(C) Dynamometer

(D) Hydrometer

4. What is the pressure indicated at the provided mercury barometer's points A, B, C, and D? Assume that you filled a tube that is longer than 76 cm fully with mercury before inverting it into a jar. Let P0 represent atmospheric pressure, g represent the gravitational acceleration, and represent the density of mercury.

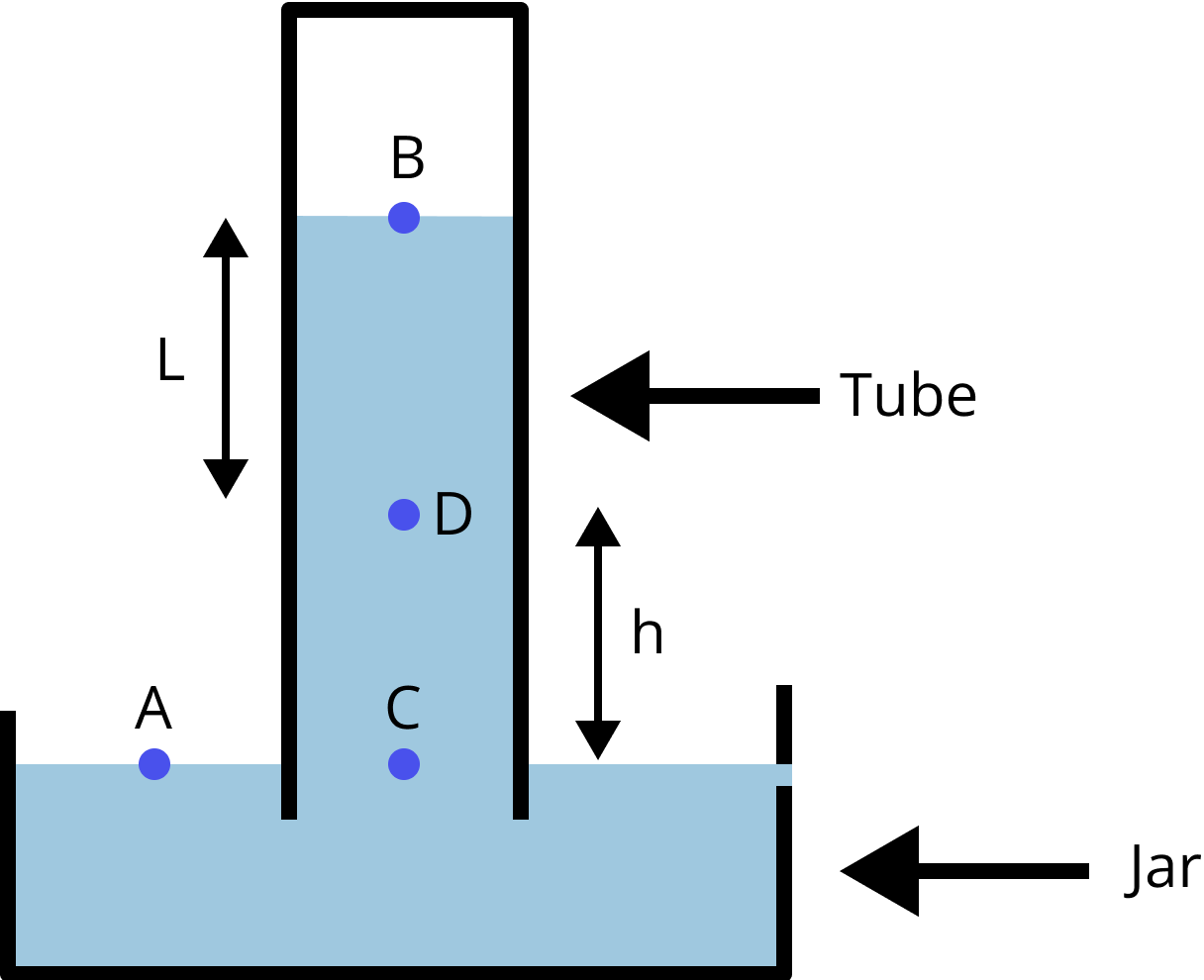
(A) $P_{A}=P_{0}, P_{B}=P_{0}, P_{C}=P_{A}, P_{D}=P_{0}+\rho g L$

(B) $P_{A}=0, P_{B}=P_{0}, P_{C}=\rho g(h+L), P_{D}=P_{0}-\rho g h$

(C) $\mathrm{P}_{\mathrm{A}}=0, \mathrm{P}_{\mathrm{B}}=0, \mathrm{P}_{\mathrm{C}}=\mathrm{P}_{0}, \mathrm{P}_{\mathrm{D}}=\mathrm{P}_{\mathrm{O}}+\rho g \mathrm{~L}$

(D) $P_{A}=P_{0}, P_{B}=0, P_{C}=P_{0}, P_{D}=\rho g L$

5. Select the appropriate streamlining option.
(A) At every point of a streamline, speed, not velocity, is the same.

(B) Laminar flow allows for the intersection of two streamlines.

(C) In the case of steady flow, streamlines have no friction.

(D) A point's velocity within a given streamline can change over time.

6. Which of the following situations allows the use of the continuity equation?
(A) Compressible flow

(B) Incompressible flow

(C) Turbulent flow

(D) Viscous flow

7. What effect does increasing temperature have on the viscosity of liquids and gases?

(A) Increases in liquids and gases

(B) Rises for liquids and falls for gases

(C) Increases in the case of gases and lowers in the case of liquids

(D) Decreases for both liquids and gases

8. Fluid (with some viscosity) flows laminarly in a closed pipe of radius R. Which point along a cross section has the fastest speed?

(A) Centre

(B) Near the wall of pipe

(C) R/2 from centre

(D) All points will have same speed

9. The contact angle controls whether a liquid rises or sinks along a solid surface. Choose the appropriate statement in this regard.

(A) If the contact angle is less than 90°, the liquid will rise along the solid surface.

(B) If the contact angle is larger than 90°, the liquid will have been depressed along the solid surface.

(C) Regardless of contact angle, liquid always rises along a solid surface.

(D) Regardless of contact angle, liquid is always depressed along a solid surface.

10. Consider a tank of height $20 \mathrm{~m}$ filled with liquid of density $100 \mathrm{~kg} / \mathrm{m}^{3}$. The area of tank is $10 \mathrm{~m}^{2}$. If the tank has a hole of area $2 \mathrm{~m}^{2}$ at the bottom, find the speed of the liquid flowing out through the hole when the height of liquid in the tank is $10 \mathrm{~m}$. Assume speed of liquid descending at top of tank is $5 \mathrm{~m} / \mathrm{s}$.

(A) $20 \mathrm{~m} / \mathrm{s}$

(B) $14.14 \mathrm{~m} / \mathrm{s}$

(C) $15 \mathrm{~m} / \mathrm{s}$

(D) $20.615 \mathrm{~m} / \mathrm{s}$

11. Work done in increasing the size of a soap bubble from a radius of $3 \mathrm{~cm}$ to $5 \mathrm{~cm}$ is nearly (Surface tension of soap solution $=0.03 \mathrm{Nm}^{-1}$,(NEET 2011)

(A) $0.2 \pi m J$

(B) $2 \pi m J$

(C) $0.4 \pi m J$

(D) $4 \pi m J$

12. A spherical solid ball of volume $V$ is made of a material of density $\rho_{1}$. It is falling through a liquid of density $\rho_{2}\left(\rho_{2}<\rho_{1}\right)$. Assume that the liquid applies a viscous force on the ball that is proportional to the square of its speed $v$, i.e., $F_{\text {viscous }}=-k v^{2}(k>0)$. The terminal speed of the ball is (NEET 2011)

(A) $\sqrt{\dfrac{V g\left(\rho_{1}-\rho_{2}\right)}{k}}$

(B) $\dfrac{V g \rho_{1}}{k}$

(C) $\sqrt{\dfrac{V g \rho_{1}}{k}}$

(D) $\dfrac{V g\left(\rho_{1}-\rho_{2}\right)}{k}$

13. If the terminal speed of a sphere of gold (density $=19.5 \mathrm{~kg} / \mathrm{m}^{3}$ ) is $0.2 \mathrm{~m} / \mathrm{s}$ in a viscous liquid (density $=1.5 \mathrm{~kg} / \mathrm{m}^{3}$, find the terminal speed of a sphere of silver (density $=10.5 \mathrm{~kg} / \mathrm{m}^{3}$ ) of the same size in the same liquid (NEET 2011)

(A) $0.4 \mathrm{~m} / \mathrm{s}$

(B) $0.133 \mathrm{~m} / \mathrm{s}$

(C) $0.1 \mathrm{~m} / \mathrm{s}$

(D) $0.2 \mathrm{~m} / \mathrm{s}$

14. If $S$ is stress and $Y$ is young's modulus of material of a wire, the energy stored in the wire per unit volume is (NEET 2011)

(A) $\dfrac{S^{2}}{2 Y}$

(B) $2 S^{2} Y$

(C) $\dfrac{S}{2 Y}$

(D) $\dfrac{2 Y}{S^{2}}$

15. A radiation of energy $E$ falls normally on a perfectly reflecting surface. The momentum transferred to the surface is (NEET 2011)

(A) $E c$

(B) $2 E / c$

(C) $E / c$

(D) $E / c^{2}$

16. Spherical balls of radius $R$ are falling in a viscous fluid of viscosity $\eta$ with a velocity $v$. The retarding viscous force acting on the spherical ball is (NEET 2011)

(A) inversely proportional to both radius $R$ and velocity $v$

(B) directly proportional to both radius $R$ and velocity $v$

(C) directly proportional to $R$ but inversely proportional to $v$

(D) inversely proportional to $R$, but directly proportional to velocity $v$

17. If two soap bubbles of different radii are connected by a tube (NEET 2011)

(A) air flows from the smaller bubble to the bigger

(B) air flows from bigger bubble to the smaller bubble till the sizes are interchanged

(C) air flows from the bigger bubble to the smaller bubble till the sizes become equal

(D) there is no flow of air.

18. A wire fixed at the upper end stretches by length $l$ by applying a force $F$. The work done in stretching is (NEET 2011)

(A) $2 \mathrm{Fl}$

(B) $\mathrm{Fl}$

(C) $\dfrac{F}{2 l}$

(D) $\dfrac{F l}{2}$

19. A cylinder of height $20 \mathrm{~m}$ is completely filled with water. The velocity of efflux of water (in $m s^{-1}$ ) through a small hole on the side wall of the cylinder near its bottom is(NEET 2010)

(A) 10

(B) 20

(C) $25.5$

(D) 5

20. A force is delivered to a 3m-side cube. A force double the amount of the previous force is delivered to a 1m cube. What is the pressure on the first cube (P) divided by the pressure on the second cube (P')?

(A) $1 / 9$

(B) 18

(C) $1 / 18$

(D) $1 / 2$

21. A tall cylinder is filled with viscous oil. A round pebble is dropped from the top with zero initial velocity. The plot shown in the figure indicates the one that represents the velocity (v) of the pebble as a function of time (t).

22. Which of the following diagrams does not represent a streamlined flow?

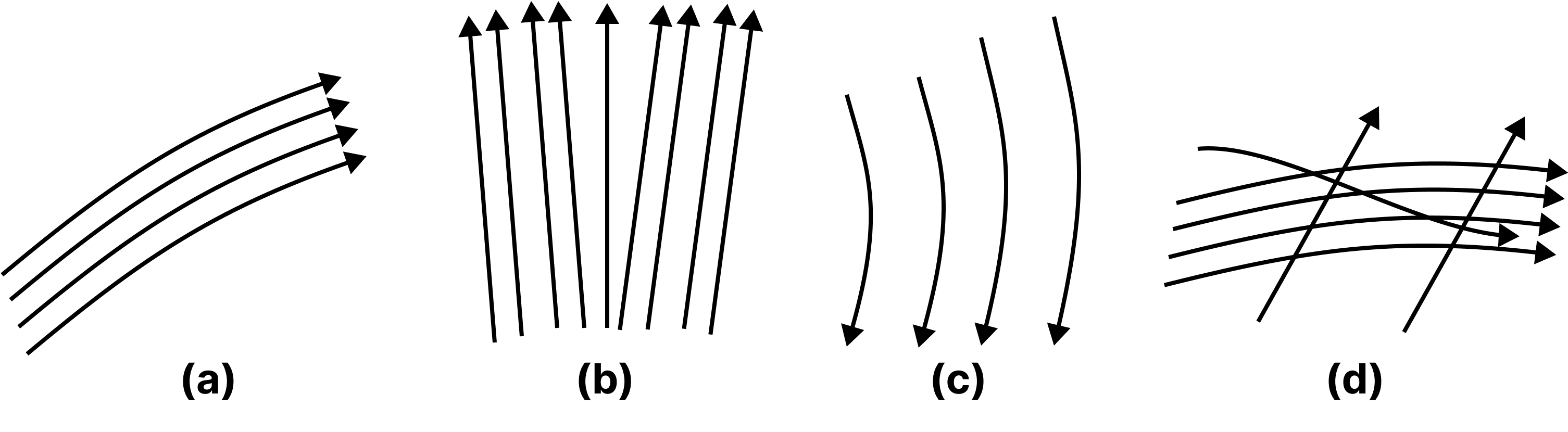
Options for Question

23. Along a streamline 

(A) the velocity of a fluid particle remains constant. 

(B) the velocity of all fluid particles crossing a given position is constant. 

(C) the velocity of all fluid particles at a given instant is constant. 

(D) the speed of a fluid particle remains constant.

24. An ideal fluid flows through a pipe of circular cross-section made of two sections with diameters $2.5 \mathrm{~cm}$ and $3.75 \mathrm{~cm}$. The ratio of the velocities in the two pipes is

(A) $9: 4$

(B) $3: 2$

(C) $\sqrt{3}: \sqrt{2}$

(D) $\sqrt{2}: \sqrt{3}$

25. The angle of contact at the interface of water-glass is $0^{\circ}$, Ethylalcohol-glass is $0^{\circ}$, Mercury-glass is $140^{\circ}$ and Methyliodideglass is $30^{\circ}$. A glass capillary is put in a trough containing one of these four liquids. It is observed that the meniscus is convex. The liquid in the trough is 

(A) Water

(B) Ethylalcohol

(C) Mercury

(D) methyliodide.

Solutions:

1. (D)
Newton's Third Law states that every action has an equal and opposite response.

Newton's Second Law states that force is the time rate of change of momentum.

Pressure is directly proportional to temperature and constant volume and mass for an ideal gas - Ideal Gas Law

Pascal's Law states that a pressure change at any point in a fluid is propagated throughout the fluid, causing the identical change to occur everywhere.

2. (A)

According to Pascal's Law, a pressure change at any point in a fluid is propagated throughout the fluid, causing the identical change to occur everywhere. This is used in hydraulic devices by altering cross-sectional areas at specific locations.

3. (B)

A barometer is an instrument for measuring air pressure. An odometer is a device that calculates the distance travelled by a wheeled vehicle (it is the speed indicator in your vehicle). A dynamometer is a device that measures the torque or revolutions per minute of an engine. A hydrometer is a device used to determine the specific gravity of liquids. Remember that the liquid used in a barometer is mercury.

4. (D)

The presumption made in the question is to guarantee that vacuum is formed when the tub is inverted into the jar and the pressure on the tube's top remains zero.

Point $A$ is present in the atmosphere, $P_{A}=P_{0}$.

Point $B$ is the top layer exposed to vacuum so $P_{B}=0$.

Point $C$ is on the same level as that of $A$, and the fluid is stationary, so $P_{C}=P_{A}=P_{0}$. Point $D$ is at a depth $L$ below point $B$ so $P_{D}=0+\rho g L$.

$\therefore$ the correct option is $P_{A}=P_{0}, P_{B}=0, P_{C}=P_{0}, P_{D}=\rho g L$.

Also note that we can write $P_{D}$ as $P_{0}-\rho g h$ and $P_{C}$ as $\rho g(L+h)$.

5.(D)

When a pipe's diameter varies, we can argue that different locations in the streamline are moving at varying speeds. Two streamlines cannot overlap because at the point of intersection, we will be unable to draw a single tangent, which indicates the direction of velocity at that location. If there are streamlines with differing velocities adjacent to each other in a pipe during constant flow, there will be friction between the streamlines, which is referred to as viscosity. The velocity of a point in a streamline can alter if the flow is erratic but not turbulent. For instance, if we gradually speed up a tap, the flow will be laminar and the speed of a point (on a streamline) will rise over time.

6. (B)

We assume that the flow is incompressible, laminar, and non-viscous to use the continuity equation. The choice implies that a fluid's density can alter when it says compressible flow. Thus, it is untrue. The answer that specifies turbulent flow is untrue since the continuity equation requires that flow be laminar. The answer that mentions viscous flow is likewise untrue as the equation of continuity requires frictionless flow.

7. (C)

When the temperature of a liquid rises, the viscosity falls because molecular bonds (electromagnetic forces) between particles weaken due to random motion caused by the rise in temperature. Gas molecules vibrate more erratically, causing more obstacle in the path of bodies attempting to move through it. And we interpret the increased blockage as higher gas viscosity.

8. (A)

We know that the shear strain rate equals v/l, where v is the velocity of the layer and l is the distance between that layer and the layer with zero speed. In this case, the layer in touch with the pipe wall will have zero speed. As a result, as one moves away from the wall, the velocity increases and reaches its maximum near the centre.

9. (A)

A liquid rises or depresses along a solid surface until its surface is perpendicular to the net force. Fluid particles are affected on by forces from solid and liquid particles, as well as gravity, near the solid and water boundary. If the resultant force vector on those fluid particles passes through a solid surface, the fluid surface must rise to ensure that the net force is perpendicular to its surface. When the liquid rises, the contact angle decreases to less than 90°.

10. (C)

Because the regions are comparable, we cannot assume the efflux speed to be $\sqrt{2 g h}$. So we apply Bernoulli's theorem between the tank's top and the hole. Because the top of the tank and the hole are exposed to the atmosphere, the pressure will be the same, equal to $P_{0}$.

$\mathrm{P}_{0}+\rho g \mathrm{H}+1 / 2 \rho v_{1}^{2}=\mathrm{P}_{0}+1 / 2 \rho v_{2}^{2}$ 

$\therefore v_{2}=\sqrt{2\left(g h+v_{1}^{2} / 2\right)}$

$=\sqrt{2(10 \times 10+25 / 2)}$ 

$=15 \mathrm{~m} / \mathrm{s}$

11. (C)

$W=T \times$ change in surface area

$W=2 T 4 \pi\left[(5)^{2}-(3)^{2}\right] \times 10^{-4}$ 

$=2 \times 0.03 \times 4 \pi[25-9] \times 10^{-4} J $

$=0.4 \pi \times 10^{-3} J $

$=0.4 \pi m J$

12. (A) 

The forces acting on the ball -

(1) $\mathrm{mg}=V \rho_{1} g$ downward direction

(2) Thrust upward direction ( By Archimedes principle )

(3) Force of friction ( Buoyant force) upward direction

The ball reaches to its terminal speed $\left(v_{t}\right)$ when acceleration $=0$.

So, weight $=$ Buoyant force $+$ Viscous force

$\therefore V \rho_{1} g=V \rho_{2} g+k v_{t}^{2}$

$\therefore v_{t}=\sqrt{\dfrac{V g\left(\rho_{1}-\rho_{2}\right)}{k}}$

13. (C)

Let Terminal velocity $=v_{t}$

Upward viscous force $=$ downward weight of sphere

$\Rightarrow 6 \pi \eta r v_{t}=\left(\dfrac{4}{3} \pi r^{3}\right)(\rho-\sigma) g$

$\Rightarrow v_{t}=\dfrac{2 r^{2}(\rho-\sigma) g}{9 \eta} \ldots \ldots . . Option (1)$

where, $\rho=$ density of substance of a body

$\sigma=$ density of liquid

Now let the terminal velocity of gold $=\mathrm{v}_{\mathrm{g}}$ and silver $=\mathrm{v}_{\mathrm{S}}$.

From equation (1), we can write

$\dfrac{v_{g}}{v_{s}}=\dfrac{\rho_{g}-\sigma}{\rho_{s}-\sigma}=\dfrac{19.5-1.5}{10.5-1.5}=\dfrac{18}{9}=\dfrac{2}{1}$

$\therefore v_{s}=\dfrac{v_{g}}{2}=\dfrac{0.2}{2}=0.1$

14. (A)

Energy stored per unit volume of wire,

$E=\dfrac{1}{2} \times \text { stress } \times \text { strain }$

$\therefore E=\dfrac{1}{2} \times \text { stress } \times \dfrac{\text { stress }}{Y}=\dfrac{1}{2} \dfrac{S^{2}}{Y}$

[ As Young's modulus $(Y)=\dfrac{\text { Stress }}{\text { Strain }}$

$\left.\therefore \text { Strain }=\dfrac{\text { Stress }}{Y}\right]$

15. (B) 

Momentum of photon $=\dfrac{E}{c}$

Change in momentum $=\dfrac{2 E}{c}$

$=$ momentum transferred to the surface

(the photon will reflect with same magnitude of momentum in opposite direction)

16. (B)

From Stoke's law,

viscous force acting on the ball falling into a viscous fluid

$F=6 \pi \eta R v$

$\therefore F \propto R$ and $F \propto v$

hence $F$ is directly proportional to radius & velocity.

17. (A)

Pressure inside the bubble, $\mathrm{P}=p_{0}+\dfrac{4 T}{R}$

So $P \propto \dfrac{1}{R}$ where $\mathrm{R}$ is the radius of the bubble. It means pressure inside a smaller bubble is greater than the inside of a bigger bubble.

So when two bubbles are connected by a tube, air will flow from the smaller bubble to the bigger bubble and the size of the bigger bubble will increase.

18. (D)

Work done by constant force in displacing the object by a distance $\ell$.

$=$ Potential energy stored

$=\dfrac{1}{2} \times \text { Stress } \times \text { Strain } \times \text { Volume }$ 

$=\dfrac{1}{2} \times \dfrac{F}{A} \times \dfrac{l}{L} \times A L $

$=\dfrac{1}{2} F l$

19. (B)

The velocity of efflux of water is given $v=\sqrt{2 g h}$

Here $h$ is the height of the free surface of water from the hole

$\therefore v=\sqrt{2 \times 10 \times 20}=20 \mathrm{~m} / \mathrm{s}$

20. (C)

$P=F / 3^{2}$

$\mathrm{P}=\mathrm{F} / 9$

$\mathrm{P}^{\prime}=2 \mathrm{~F} / 1^{2}$ 

$\mathrm{P}^{\prime}=2 \mathrm{~F} / 1 $

$\mathrm{P} / \mathrm{P}^{\prime}=(\mathrm{F} / 9) /(2 \mathrm{~F} / 1) $

$=1 / 18$

21. (C)

When the pebble is falling through the viscous oil, the viscous force (drag force) acting on pebble is,

$\mathrm{F}=6 \pi \mathrm{rnv}$

The direction of viscous force $\left(F_{v}\right)$ and buoyant force $\left(F_{b}\right)$ will be opposite to that of velocity.

However, weight of the body acting downwards, tends to accelerate the body. Initially $W>F_{v}+F_{b}$, hence the pebble will accelerate.

With increase in $v, F_{v}$ increases. This diminishes the acceleration of the pebble.

At some instant, $W=F_{v}+F_{b}$ and net force on pebble $F_{\text {net }}=0$

$\Rightarrow \mathrm{a}=\mathrm{O}$

The pebble will move at constant velocity $v=v_{T}$, called terminal velocity.

As the force is variable, hence acceleration is also variable, so $v$ - t graph will not be a straight line. Velocity increases first and then become constant. $\therefore$ (C) is correct.

22. (D)

A streamline can be straight or curved, with the tangent indicating the velocity direction. Because crossing two streamlines would suggest two velocities at the place of intersection, which is impossible, ( d ) does not reflect a streamlined flow.

23. (C)

Along a streamline, Av = constant. This means that at a particular cross-section, the velocity of all fluid particles is constant. Hence, we can say that the velocity of all fluid particles crossing a given position is constant.

24. (A)

According to equation of continuity $\mathrm{A}_{1} \mathrm{v}_{1}=\mathrm{A}_{2} \mathrm{v}_{2}$

$\dfrac{\mathrm{v}_{1}}{\mathrm{v}_{2}}=\dfrac{\mathrm{A}_{1}}{\mathrm{~A}_{2}}=\dfrac{\pi \mathrm{D}_{2}^{2} / 4}{\pi \mathrm{D}_{1}^{2} / 4}=\left(\dfrac{\mathrm{D}_{2}}{\mathrm{D}_{1}}\right)^{2}$

Here, $\mathrm{D}_{1}=2.5 \mathrm{~cm}, \mathrm{D}_{2}=3.75 \mathrm{~cm}$

$\therefore \dfrac{\mathrm{v}_{1}}{\mathrm{v}_{2}}=\left(\dfrac{3.75}{2.5}\right)^{2}=\left(\dfrac{3}{2}\right)^{2}=\dfrac{9}{4}$

25. (C)

Water glass has a contact angle of $0^{\circ}$, ethyl alcohol glass has a contact angle of $0^{\circ}$, mercury glass has a contact angle of $140^{\circ}$, and methyl iodide glass has a contact angle of $30^{\circ}$. A glass capillary is placed in a trough containing one of these four liquids. The meniscus is found to be convex. Mercury is the liquid in the trough. A convex meniscus is only possible when the angle of contact is obtuse. Among the liquids available, only the mercury-glass pair fits this criterion.

Importance of Mechanical Properties of Fluids

This is an important chapter of the Class 11 Physics NEET syllabus. It teaches the various mechanical properties exhibited by the fluids only. It will introduce the students to pressure in fluids, Pascal’s Law to calculate pressure, and Archimedes Principle to find out why objects float or submerge in a fluid.

This chapter will explain why all the fluids are different in terms of their mechanical properties. Students will learn the scientific reasons behind the floatation of objects in fluids. They will learn what factors decide the degree of floatation of an object in a particular fluid.

On proceeding further, students will be taught about the equation of continuity to explain the flow of a fluid in a pipe. This chapter is important as it introduces the basic level of fluid dynamics to the NEET aspirants.

Students will also learn how to calculate the energy level of a fluid. They will find out that fluids have three kinds of energy. Solids do not have pressure energy but fluids do. These types of energies will be explained and defined using mathematical expressions. If you refer to the Mechanical Properties of Fluids notes, you will be able to understand these scientific terms related to fluids easily.

Benefits of Vedantu’s Mechanical Properties of Fluids NEET Revision Notes

• These revision notes of Mechanical Properties of Fluids will help you to get a concise version of this entire chapter on fluid mechanics. The basic and advanced scientific principles will be explained in simpler terms so that you can imbibe the main concepts easily.

• The concise version of the Mechanical Properties of Fluids NEET notes will also help you to revise this chapter faster by comprehending the meaning and implications of fundamental terms of fluid mechanics. It will also become easier to apply the formulas and answer questions accurately.

• Use the Mechanical Properties of Fluids NEET questions to check your preparation level. Find out the areas of this chapter you need to focus on more. These revision notes offer a unique tool to evaluate your preparation level. Check how the experts have answered these fundamental questions and escalate your answering skills.

• Make yourself more efficient in recalling the concepts during an exam by memorising the concise format of the description of this chapter in these notes.

Download Free Mechanical Properties of Fluids Revision Notes PDF

Students can download the free PDF version of this chapter now and complete their study material. Discover the best way to revise and recall all the concepts of mechanical properties of the fluid in no time. Understand how a fluid flows and what properties it exhibits. Get the simplest explanation of all the theorems and laws in this chapter to develop a strong conceptual foundation.