Crystal Field Theory in Square Planar Complexes - NEET Important Topic

The crystal field theory is a model that explains the observed physical and chemical properties of transition metal complexes. The theory is based on the idea that when transition metals form complexes, the ligands (atoms or molecules that are bonded to the metal) interact with the metal's d orbitals. These interactions split the d orbitals into two energy levels: an "e" level and an "t" level. The e level is lower in energy than the t level, so electrons tend to occupy the e orbitals. This splitting of energy levels results in certain characteristic properties of transition metal complexes, such as colour, magnetism, and reactivity.

Note: 👉Get a Head Start on Your Medical Career with the NEET Rank and College Predictor 2024.

Understanding the Crystal Field Theory

To clearly understand the crystal field interactions in transition metal complexes, knowledge of the geometrical or spatial disposition of d orbitals is required. In a free gaseous metal ion, the d-orbitals are five fold degenerate. If a spherically symmetric field of negative ligand field charge is imposed on a central metal ion, the d-orbitals remain degenerate but the energy of the free ion changes.

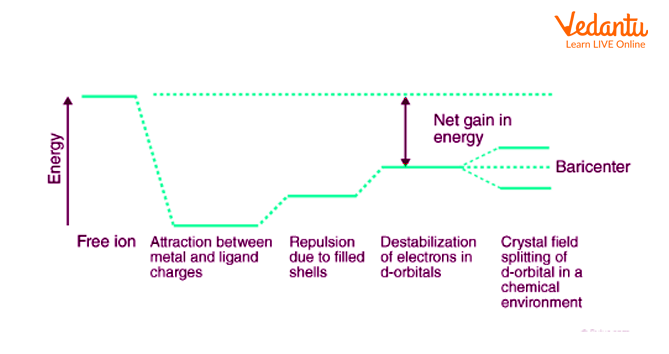
Crystal Field Theory

The metal-ligand bond was described as an ionic bond arising solely from electrostatic interactions between metal ions and ligands by crystal field theory. Anions are treated as point charges in crystal field theory, while neutral molecules are treated as dipoles.

When transition metals aren't bonded to anything, their d orbitals degenerate, which means that they have the same energy. When they begin bonding with other ligands, the d orbitals split apart and become non-degenerate due to different symmetries of the d orbitals and the inductive effect of the ligands on the electrons.

What is High Spin and Low Spin?

The complexion with the most unpaired electrons is known as the high spin complex, while the complexion with the fewest unpaired electrons is known as the low spin complex. With weak field ligands, high spin complexes are expected because the crystal field splitting energy is low. The opposite is true for low spin complexes, where strong field ligands cause maximum electron pairing in the set of three ${{t}_{2}}$ atomic orbitals due to large ${{\Delta }_{0}}$.

High spin implies the greatest number of unpaired electrons.

Low spin implies a small number of unpaired electrons.

Taking the example: \[{{\left[ Co{{\left( CN \right)}_{6}} \right]}^{3-}}\text{  }\!\!\And\!\!\text{  }{{\left[ Co{{F}_{6}} \right]}^{3-}}\]

\[{{\left[ Co{{\left( CN \right)}_{6}} \right]}^{3-}}:\] Low spin complex

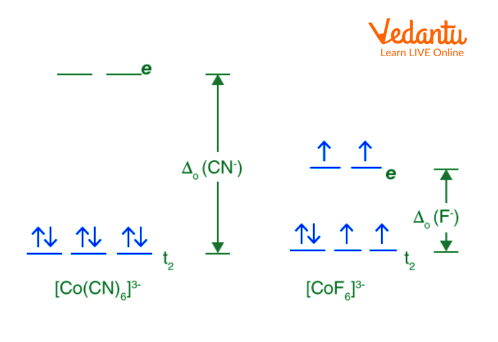
High Spin and Low Spin of Above Example

The terms "high spin" and "low spin" can be used to describe both atoms and molecules. However, they are most commonly used to describe transition metal complexes. Transition metal complexes are molecules that contain a central metal ion bonded to one or more ligands (atoms or groups of atoms). The ligands can be either organic or inorganic molecules.

The type of bonding between the metal ion and ligand(s) determines whether the complex will have a high spin or low spin configuration. If the bond is covalent, 

(i) then the complex will have a low spin configuration. However, if the bond is ionic,

(ii) then the complex will have a high spin configuration.

The number of unpaired electrons also determines whether a complex will have a high-spin or low-spin configuration. If there are more than four unpaired electrons, then the complex will have a high-spin configuration; if there are four unpaired electrons or fewer, then the complex will have low spin configuration. Complexes with more than four unpaired electrons are rare because it is difficult to stabilise such highly energetic molecules.

Crystal Field Splitting in Square Planar Complex

The crystal field splitting in a square planar complex is the result of the different arrangements of the ligands around the central metal ion. In a square planar complex, there are four ligands arranged in a square planar shape around the metal ion. The two ligands in the x-axis have a different arrangement than the two ligands in the y-axis. This results in a different crystal field splitting for these two sets of ligands. The x-axis ligands experience a higher crystal field splitting than the y-axis ligands. This results in a higher energy for the x-axis orbitals and a lower energy for the y-axis orbitals.

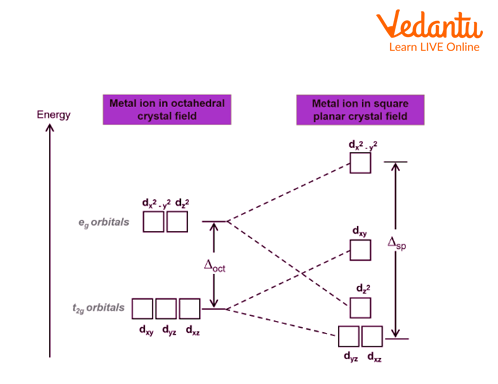
Representing Crystal Field Splitting in Square Planar Complex

A square planar complex is a type of coordination complex in which the central metal ion is surrounded by four ligands arranged in a square. This arrangement is possible when the central metal ion has \[{{d}^{0}},\text{ }{{d}^{8}},\text{ }or\text{ }{{d}^{10}}\]electron configuration, as these configurations have no unpaired electrons and thus can accommodate more ligands. Square planar complexes are often used in catalysis and as sensors.

Let’s go through an example to understand the square planar complex. In \[{{\left[ Ni{{\left( CN \right)}_{4}} \right]}^{2-}}\]ion complex, the valence shell electronic configuration of Ni (o.s. +2) is $3{{d}^{8}}$. Since CN^– is a strong ligand, therefore, pairing of two unpaired electrons of 3d orbitals takes place resulting in a vacant d orbital. This vacant 3d orbital gets hybridised with the vacant 4s and two of 4p orbitals to give four \[ds{{p}^{2}}\]hybrid orbitals. This leads to the formation of square planar geometry and the magnetic moment is zero. Hence, the complex is diamagnetic.

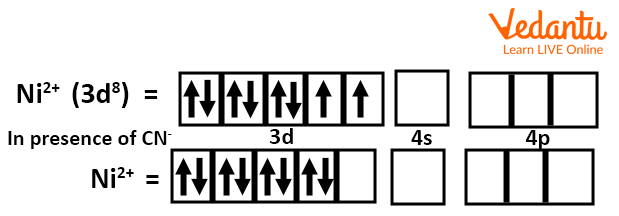
Electronic Configuration of Ni

Electronic Configuration of (Ni(Cn))₄^2- ion

Summary

The crystal field theory is a model that explains the observed physical and chemical properties of transition metal complexes. It is based on the idea that when transition metals form complexes, the ligands (atoms or molecules) that are bonded to the metal interact with the metal's d orbitals. In crystal field theory, "high spin" refers to an electronic configuration in which all of the electrons are paired up and there are no unpaired electrons. In a low spin configuration, there is at least one unpaired electron. Transition metal complexes are molecules that contain a central metal ion bonded to one or more ligands (atoms or groups of atoms).

The type of bonding between the metal ion and ligand(s) determines whether the complex will have a high spin or low spin configuration. In a square planar complex, there are four ligands arranged in the form of a square planar structure around the main metal ion. This results in a different crystal field splitting for these two sets of ligands.