Understanding Hundredth Maths

What is a Hundredth?

Let us assume that you have 100 friends in your colony and one day, you receive a cash prize of Rs. 100 after clearing Maths olympiad. The next day, all of your friends appear in your room and ask for their share. So, now a dilemma is how to solve this issue and divide equal share among all of your friends. Now, what you do is take 1/100 of the share and give it to each of your friends. So, here 100 Rs is what you have and then dividing it by 100, i.e., 100/100 = 1. Now, Rs. 1 is that you gave to your first friend, and subsequently, you gave this 100 times, which means each of your 100 friends gets Re. 1.

A question arises: what does 1/100 mean here? Well, 1/100 is the hundredth, and in this article, we will study how to divide any number into 100 equal parts. Now, let us proceed with solved examples on the concept of the hundredth.

Example of Hundredth in Maths

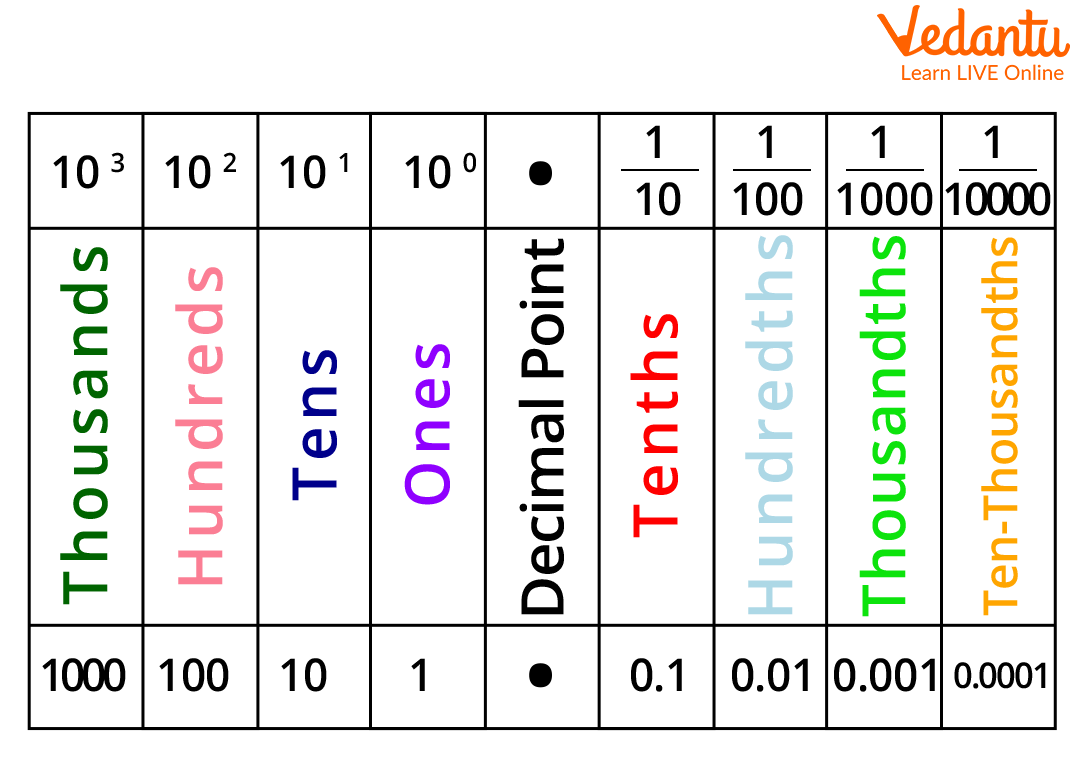
Let us consider a big number 3456.872 and find the place value of each digit to determine where the position of the hundredth falls.

Here, we have the following place values:

• 6 has a place value of ones, so 6 x 1 = 6.

• 4 has a place value of tens, so 4 x 100 = 400.

• 5 has a place value of hundreds, so 5 x 100 = 500.

• Similarly, 3 has a place value of thousands, so 3 x 1000 = 3000.

• Now, going to the digits right after the decimal, we have the following place values:

• 8 has a place value of the tenth of 8, so 8/10th or 0.8.

• 7 has a place value of hundredth of 7, so 7/100th or 0.07.

• 2 has a place value of thousandth of 2, i.e., 2/1000th or 0.002.

So, here you can notice the place value of 7 corresponding to the hundredth is 7/100th or 0.07.

Now, let us take another example to understand this concept a bit more. So, we have a number 2465.235. Now, let us solve this:

• 5 has a place value of ones, so 5 x 1 = 5.

• 6 has a place value of tens, so  6 x 10 = 60.

• 4 has a place value of hundreds, so 4 x 100 = 400.

• Similarly, 2 has a place value of thousands, so 2 x 1000 = 2000.

Now, going to the digits right after the decimal, we have the following place values:

• 2 has a place value of the tenth of 2, so 2/10th or 0.2.

• 3 has a place value of hundredth of 3, so 3/100th, i.e., 0.03.

• 5 has a place value of thousandth of 5, i.e., 5/1000th or 0.005.

So, here you can notice the place value of 3 corresponding to the hundredth is 3/100th or 0.03.

This is how we understand the position of the hundredth in a given number with the help of the place value concept.