




How to Create and Interpret Frequency Tables in Maths
What is a Frequency?
The number of times a particular data value occurs in a given data set is referred to as its frequency. Let us understand the concept of the frequency with a simple example of grades obtained by the students of your group in the Maths project. Let’s say there are 10 students in your project group, and three of you obtained grade A in the project. Four of the students in your group get a B+, two students score a C, and one student scores D. Now, let us note down the grades obtained by each of you in a series.
A, A, A, B, B, B, B, C, C, D
Count the number of times each grade occurs in the above series. Yes, ‘A’ occurs thrice, ‘B+’ occurs four times, ‘C’ occurs twice, and ‘D’ occurs once. Now, according to the definition of frequency, we can note the frequency of each grade as follows:
Frequency of A = 3
Frequency of B = 4
Frequency of C = 2
Frequency of D = 1
Let us now learn about the frequency table.
What is a Frequency Table?
A frequency table consists of the lists of items in a given data set and the number of times each item occurs in the data set.
Let us list the grades obtained by the students in the above example, in a frequency table.
To be more precise, here, in the above table, we have arranged the data (or grades) alongside their corresponding frequencies. The data values are listed in ascending order in frequency tables.
What are Tally Marks?
Let us now understand tally marks in a frequency table. Tally marks make an easy way to note and record the frequencies of the values in a given data set. The frequencies 1 to 4 are represented by short straight lines, quite like the Roman 1, in tally. The below-given picture shows the tally marks for frequencies from 1 to 10.
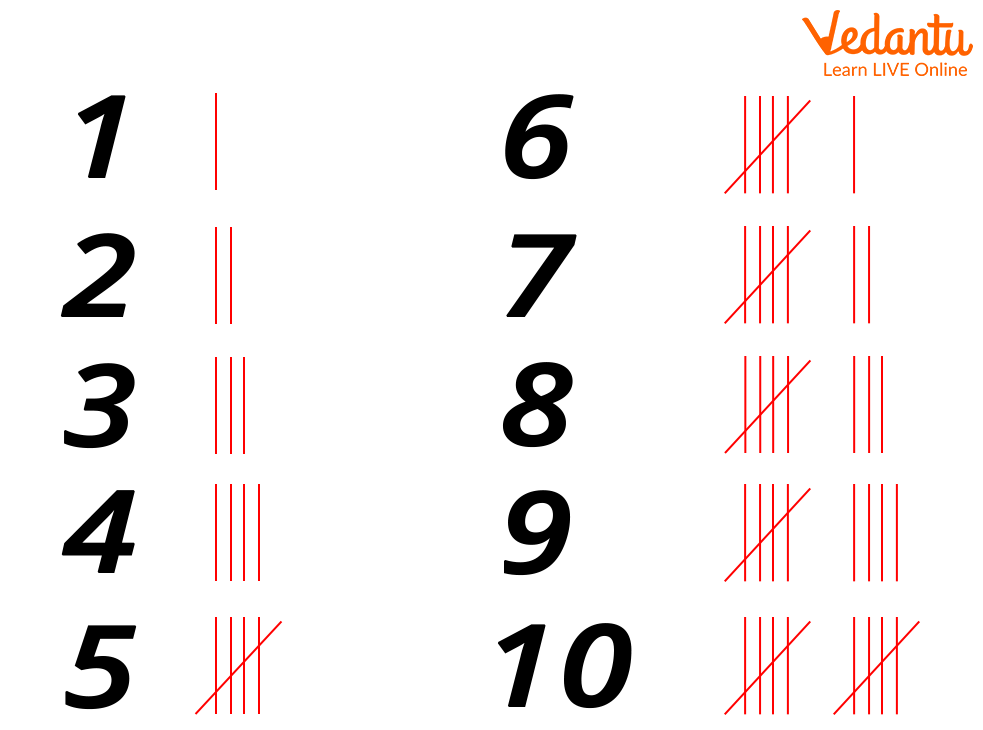
Tally marks
For frequency 1, the tally marks will be ‘I’; for frequencies 2, 3, and 4, the tally marks will be represented by repeating ‘I’ as many times as the frequency. However, the tally marks for frequency 5 is represented by oblique strike-through on the tally marks for 4.
Again, we represent frequency 6 as ‘I’ after the tally for 5. The same process is repeated to represent the rest of the frequencies in tally marks.
How to Create a Frequency Table?
Step 1: Make a table with three columns.
Step 2: List the data in ascending order in the first column.
Step 3: The second column is for tally marks. Count the number of times each data value occurs in the given data set and write the tally marks accordingly.
Step 4: The third column is for frequencies. Count the tally marks in the second column for each data value and write the corresponding frequency in the third column.
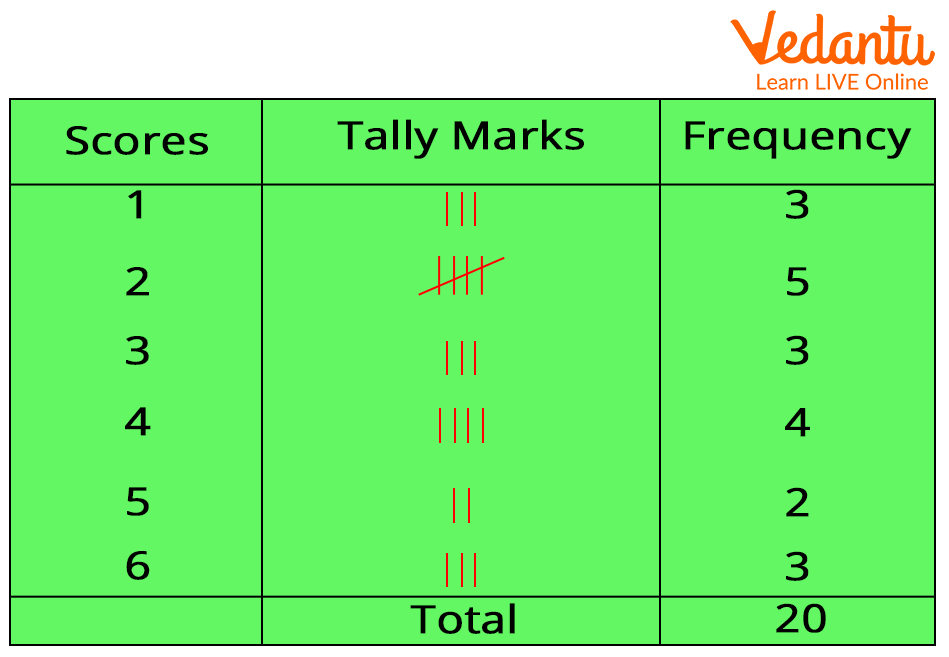
Frequency Table Example
Solved Examples
Let us now go through a few solved examples on frequency tables.
Example 1:
The marks obtained in an English test by a class of 20 students are given below.
(Full marks: 30)
25, 23, 28, 21, 24, 23, 23, 25, 22, 21, 28, 21, 23, 25, 28, 21, 25, 24, 22, 22
Represent the above-given marks in a frequency table with tally marks.
Solution:
Example 2:
Mary and Alice had a basketball challenge. The basket was high enough for them and each of them was given 3 chances to score. Mary’s scores were 0, 0, and 0. Alice’s scores were 1,1, and 0. Make a frequency table for the scores of Mary and Alice in the match.
What is Class Interval?
When the data set is spread out over a long range of values, the frequency table becomes clumsy if we make a separate row for each data. So, the data is classified into equal groups or class intervals for convenience. At most, a neat frequency table can have 5 to 10 rows, and each class interval should begin with a multiple of the group size.
For example, if the chosen group size is 10, the groups should ideally begin with 10, 20, 30, 40, 50, etc. Each group is referred to as a class interval in the frequency table.
The frequency of a class interval or group is determined by the number of data values occurring in the data set from the class interval.
Solved Example
Make a frequency distribution table for the following data:
11, 22, 4, 9, 0, 23, 14, 17, 7, 3, 28, 13, 21, 29, 7, 21, 4, 30, 17, 26, 9
Solution:
Let us first understand the range of the given data set, 0 to 30.
To have 5 to 10 rows in the frequency table, we can choose a class interval of 5.
Frequency tables have applications in various fields. To strengthen the understanding of frequency and frequency tables, kids may try to count and group their toys or stationery, like pens or colour pencils, and note the numbers in a frequency table. They may also note down the scores obtained by their friends in a particular test and arrange them in a frequency distribution table. The more they apply the concept of frequency tables in their day-to-day life, the more their analytical skills will develop. Therefore, practising frequency table worksheets will help kids organise and analyse any kind of data in the long run.
FAQs on Frequency Tables Explained: Meaning, Uses & Simple Examples
1. What is a frequency table in simple terms?
A frequency table is a chart that organises data by showing the number of times each value or category appears in a dataset. It provides a clear summary, making it easier to see patterns and the most common results at a glance. For example, it can show how many students scored in different mark ranges in a test.
2. What are the key steps to create a frequency table from raw data?
To create a basic frequency table from a list of raw data, you generally follow these steps:
- First, identify all the unique data values or decide on appropriate groups (class intervals) and list them in the first column.
- Next, go through the raw data and make a tally mark in a second column next to the corresponding value or interval each time it appears.
- Finally, count the tally marks for each category and write the total numerical count, known as the frequency, in a third column.
3. What are the essential columns or components of a frequency table?
A standard frequency table has three essential components, typically organised into columns:
- Categories or Class Intervals: This column lists the specific values (e.g., shoe size 5, 6, 7) or groups (e.g., marks from 0-10, 11-20) the data is divided into.
- Tally Marks: A temporary working column used for systematically counting the occurrences of each category from the raw data.
- Frequency: This final column shows the total count for each category, representing how many times it appeared.
For more advanced analysis, a fourth column for cumulative frequency might also be included.
4. What is the importance of using tally marks when creating a frequency table?
Tally marks are important because they provide a systematic and less error-prone method for counting data points, especially with large datasets. They act as a running record, preventing you from accidentally skipping data points or double-counting them. The practice of grouping tallies in sets of five (four vertical lines and one diagonal cross) makes the final counting of the frequency quick, organised, and accurate.
5. When should you use a grouped frequency table instead of an ungrouped one?
You should use a grouped frequency table when dealing with a wide range of data or continuous data (like heights, weights, or time). An ungrouped table, which lists every single unique value, becomes too long and impractical in these cases. By grouping the data into class intervals (e.g., 50-60 kg, 60-70 kg), you can summarise the information effectively and reveal patterns that would otherwise be difficult to see in a long list of individual values.
6. What is the difference between 'frequency' and 'cumulative frequency' in a distribution table?
The key difference is what they measure. Frequency tells you the number of times a specific value or a value within a single class interval occurs. In contrast, cumulative frequency is a running total. It shows the total number of data points that fall at or below the upper limit of a particular class interval, helping you understand the total count up to that point.
7. How do frequency tables help in understanding real-world data patterns?
Frequency tables turn a confusing list of raw numbers into an organised summary that reveals important real-world patterns. They help to:
- Identify the most popular item: A shopkeeper can quickly see the best-selling product.
- Understand distribution: A teacher can see if most students scored high, low, or in the middle on a test.
- Detect anomalies: It becomes easy to spot values that are unusually high or low (outliers).
- Prepare for visualisation: The organised data is the perfect starting point for creating graphs like histograms and bar charts to present the findings visually.
8. What is a class interval, and how does its size affect the interpretation of the data?
A class interval is a range used to group data in a grouped frequency table (e.g., 10-20, 20-30). The size of this interval is crucial for interpretation:
- If the size is too small, it results in too many groups, which can be as confusing as the original raw data and may not show a clear pattern.
- If the size is too large, too much data is grouped together, which can hide important details and distort the true distribution.
Choosing a balanced class size is key to creating a table that provides a meaningful and accurate summary of the data.























