Area of Shaded Region

The area of the shaded region is basically the difference between the area of the complete figure and the area of the unshaded region. For finding the area of the figures, we generally use the basic formulas of the area of that particular figure. There is no specific formula to find the area of the shaded region of a figure as the amount of the shaded part may vary from question to question for the same geometric figure.

What is Area ?

Area is basically the amount of space occupied by a figure. The unit of area is generally square units; it may be square meters or square centimeters and so on.

Formula for Area of Geometric Figures :

• Area of a square \[ = \] side \[ \times \] side

• Area of a rectangle \[ = \] length \[ \times \] breadth

• Area of a triangle \[ = \dfrac{1}{2} \times \] base \[ \times \] height

• Area of a circle \[ = \] \[\pi {{\rm{r}}^2}\]

• Area of a parallelogram \[ = \] base \[ \times \] height

• Area of a trapezium \[ = \dfrac{1}{2}\] \[ \times \]sum of the length of the parallel sides \[ \times \] height

• Area of rhombus \[ = \dfrac{1}{2}\] \[ \times \] product of the diagonals

What is the Area of the Shaded Region ?

In a given geometric figure if some part of the figure is coloured or shaded, then the area of that part of figure is said to be the area of the shaded region.

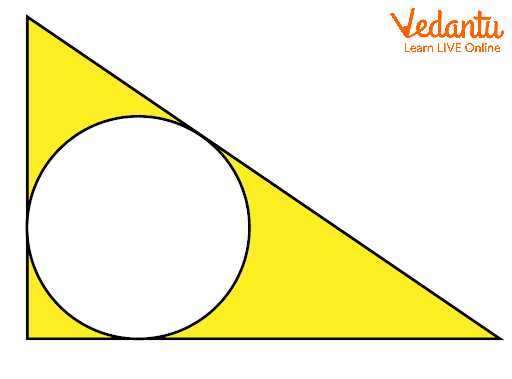
Example on how to Find Area of the Shaded Region

How to Find the Area of the Shaded Region?

So, the area of the shaded or coloured region in a figure is equal to the difference between the area of the entire figure and the area of the part that is not coloured or not shaded.

Area of the shaded region \[ = \] Area of the complete figure \[ - \] Area of the unshaded part

In the above image, if we are asked to find the area of the shaded region; we will calculate the area of the outer right angled triangle and then subtract the area of the circle from it. The remaining value which we get will be the area of the shaded region.

Solved Examples :

1. Find the area of the shaded region from the given figure :

Area of the Shaded Region

Solution :

Here, the length of the given rectangle is 48 cm and the breadth is 22 cm.

We can observe that the outer rectangle has a semicircle inside it. From the figure we can observe that the diameter of the semicircle and breadth of the rectangle are common.

So from this figure we can understand that the area of the shaded region for this figure will be equal to the difference between the area of the outer rectangle and the area of the inner semicircle.

We know that, Area of rectangle = length \[ \times \] breadth

∴ Area of the given rectangle = 48 cm \[ \times \] 22 cm \[ = 1056\] sq.cm

Also, Area of a semicircle = \[\dfrac{1}{2}\pi {r^2}\]

Here, diameter \[ = 22\] cm

So, Radius \[ = \dfrac{1}{2} \times \] Diameter \[ = \dfrac{1}{2} \times 22 = 11\]cm

Area of the given semicircle \[ = \dfrac{1}{2} \times \dfrac{{22}}{7} \times 11 \times 11 = \dfrac{{2662}}{{14}} = 190.14\]sq.cm

Therefore, Area of the shaded region = Area of rectangle - Area of semicircle

So, Area of the shaded region in the given figure = 1056 - 190.14 = 865.86 sq.cm

Area of the shaded region in the given figure is 865.86 sq.cm.

2. Find the area of the shaded region from the given figure :

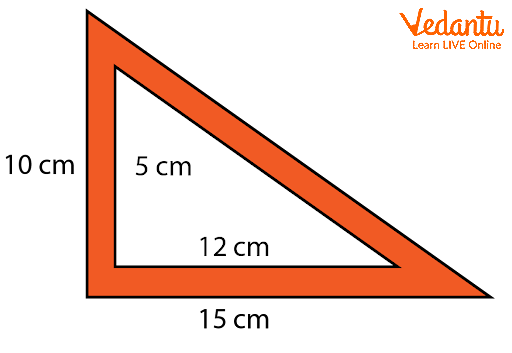
Area of the Shaded Region

Solution :

Here, the base of the outer right angled triangle is 15 cm and its height is 10 cm.

Similarly , the base of the inner right angled triangle is given to be 12 cm and its height is 5 cm.

We can observe that the outer right angled triangle has one more right angled triangle inside.

So from this figure we can understand that the area of the shaded region for this figure will be equal to the difference between the area of the outer triangle and the area of the inner triangle.

We know that, Area of a triangle \[ = \] \[\dfrac{1}{2}\] \[ \times \] base \[ \times \] height

∴ Area of the outer right

angled triangle \[ = \dfrac{1}{2} \times 15 \times 10 = \dfrac{1}{2} \times 150 = 75\] sq.cm.

Similarly, area of the inner

right angled triangle \[\dfrac{1}{2} \times 12 \times 5 = \dfrac{1}{2} \times 60 = 30\]sq.cm.

Therefore, Area of the shaded

region = Area of the outer triangle - Area of the inner triangle

We know that, Area of a triangle \[ = \dfrac{1}{2} \times {\rm{base}}\times{\rm{height}}\]

∴ Area of the outer right angled triangle \[ = \dfrac{1}{2} \times 15 \times 10 =\dfrac{1}{2}\times 150 = 75\] sq.cm.

Similarly,

area of the inner right angled triangle \[\dfrac{1}{2} \times 12 \times 5 = \dfrac{1}{2} \times 60 = 30\] sq.cm.

Therefore, Area of the shaded region \[ = \] Area of the outer triangle \[ - \] Area of the triangle. So, Area of the shaded region in the given figure \[ = 75 - 30 = 45\] sq.cm

Area of the shaded region in the given figure is 45 sq.cm.

3. Find the area of the shaded region from the given figure :

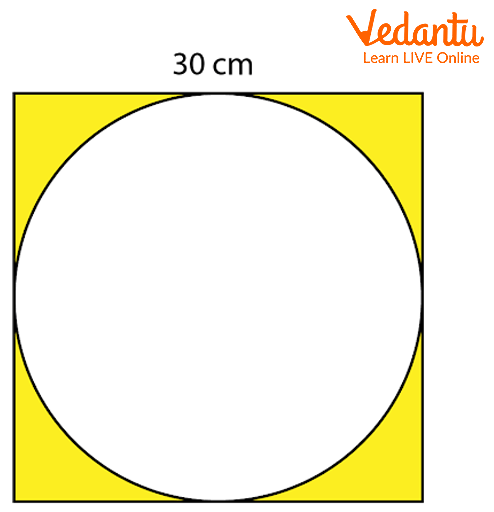
Area of the Shaded Region

Solution :

Here, the length of the side of the given square is 30 cm.

We can observe that the outer square has a circle inside it. From the figure we can see that the value of the side of the square is equal to the diameter of the given circle.

So from this figure we can understand that the area of the shaded region for this figure will be equal to the difference between the area of the outer square and the area of the inner circle. We know that, Area of square = side x side

∴ Area of the given square \[ = \] 30 cm \[ \times \] 30 cm \[ = \] 900 sq.cm

Also, Area of a circle \[ = \pi {r^2}\]

Here, diameter \[ = 30\] cm

So, Radius \[ = \dfrac{1}{2} \times \] Diameter \[ = \dfrac{1}{2} \times 30 = 15\]cm

Area of the given circle\[ = \dfrac{{22}}{7} \times 15 \times 15 = 49507 = 707.14\] sq.cm

\[ = \dfrac{{22}}{7} \times 15 \times 15 = \dfrac{{4950}}{7} = 707.14\] sq.cm

Therefore, Area of the shaded region = Area of square - Area of circle

So, Area of the shaded region in the given figure \[ = 900 - 707.14 = 192.86\] sq.cm

Area of the shaded region in the given figure is 192.86 sq.cm.

Conclusion

The area of the shaded region is in simple words the area of the coloured portion in the given figure. So, the ways to find and the calculations required to find the area of the shaded region depend upon the shaded region in the given figure.