How to Solve Subtraction Problems in Year 3 with Regrouping and Word Examples
In Standard 2, you have learned how to subtract 3-digit numbers with and without borrowing. Now, we will learn subtraction using 4 and 5-digit numbers.
Before that let us briefly revise subtraction - Subtraction has three parts, subtrahend, minuend, and the difference. Subtrahend and minuend remain at the left side of the equals to sign while the difference remains at the right of the equal to sign.
Now, we learn the concept of subtraction without and with borrowing using 4-digit or 5-digit numbers along with some solved examples. Also, we will understand how borrowing takes place while subtracting numbers.
Subtraction without Borrowing for Class 3 Students
The same 3-digit numbers subtraction method is applicable to 4-digits, 5-digits, and 6-digits numbers.
Now, let us learn 4-digits or 5-digits subtraction without borrowing. A few examples are shown below:
Example 1. Subtract 6027 from 7649 and determine the result.
Solution: First, place the digits of the numbers according to place value in column format as shown in the image.
Step 1 - Subtract the digits under ones place as shown below:
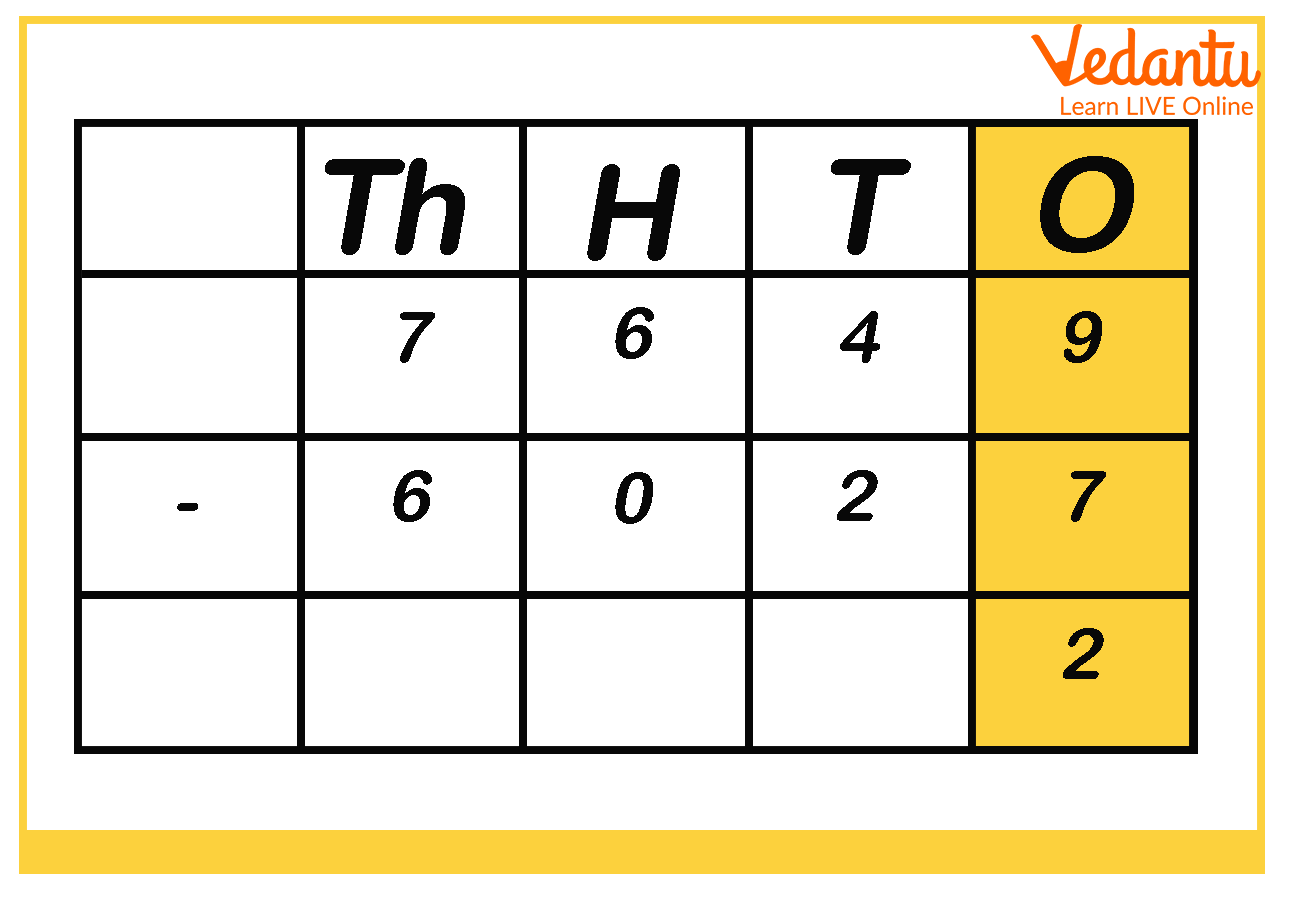
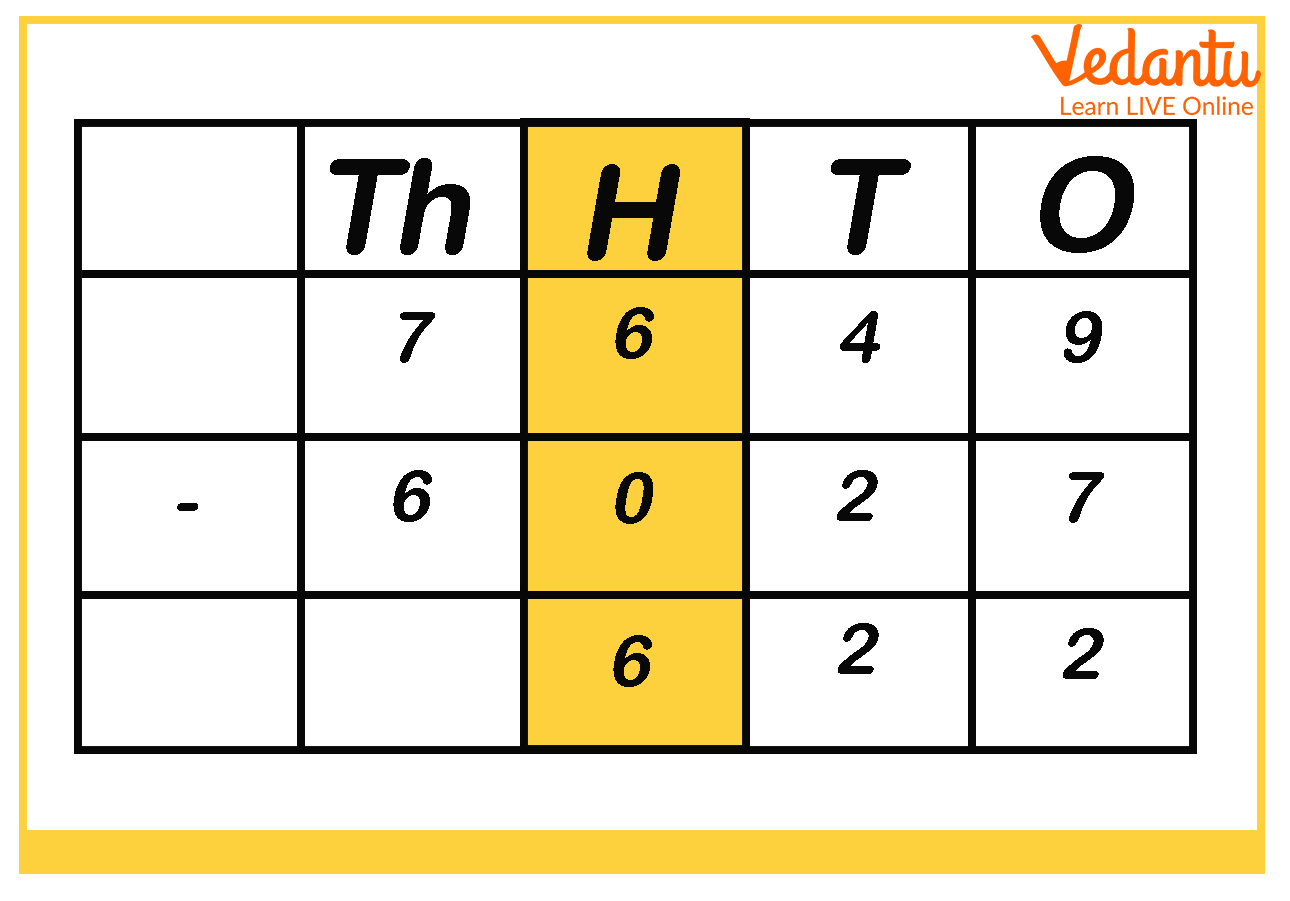
Step 2: Then, subtract the digits under tens place as you can see in the picture below.
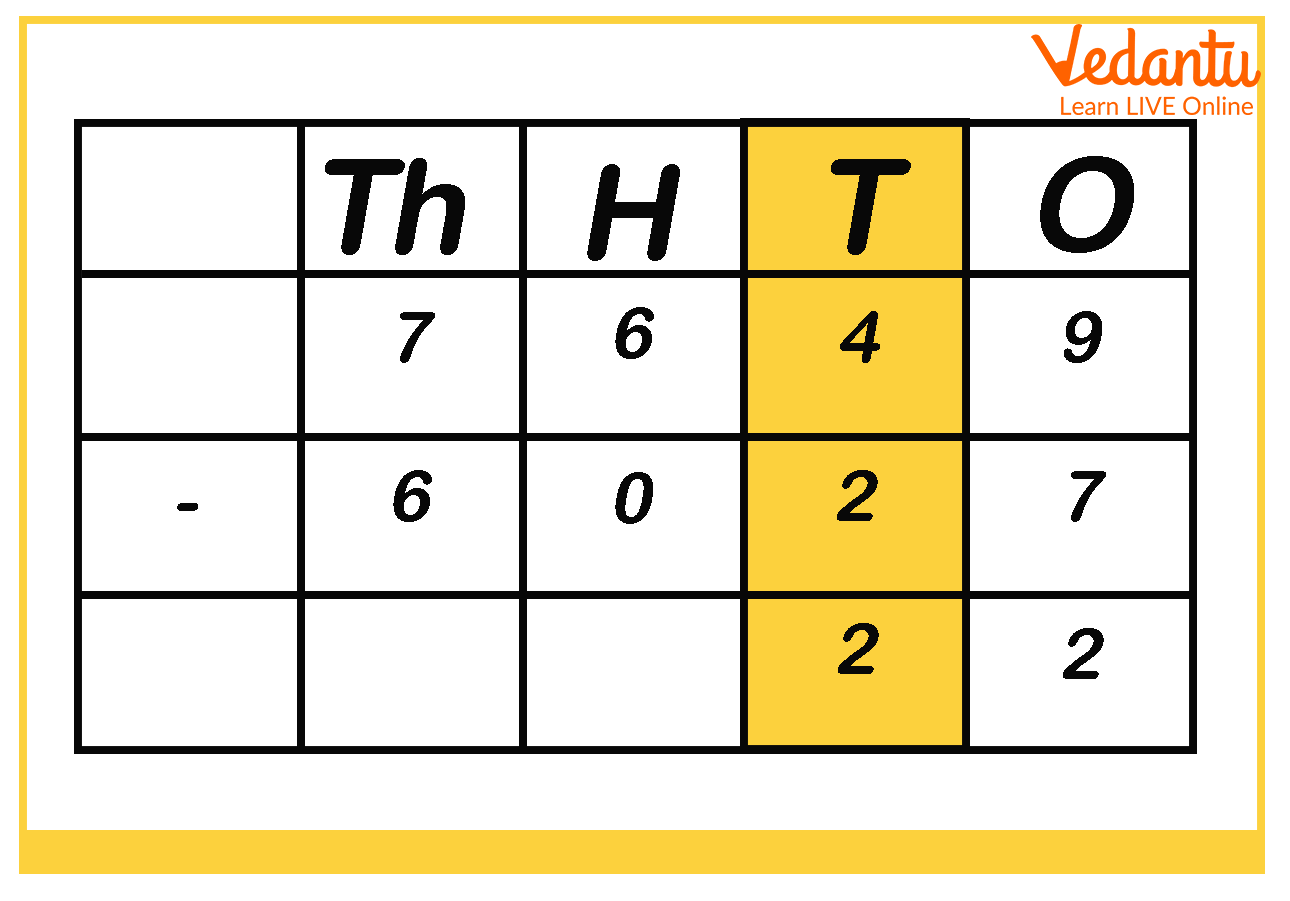
Step 3: Now, subtract the digits under hundreds place.
Step 4: Finally, subtract the digits under thousands place.
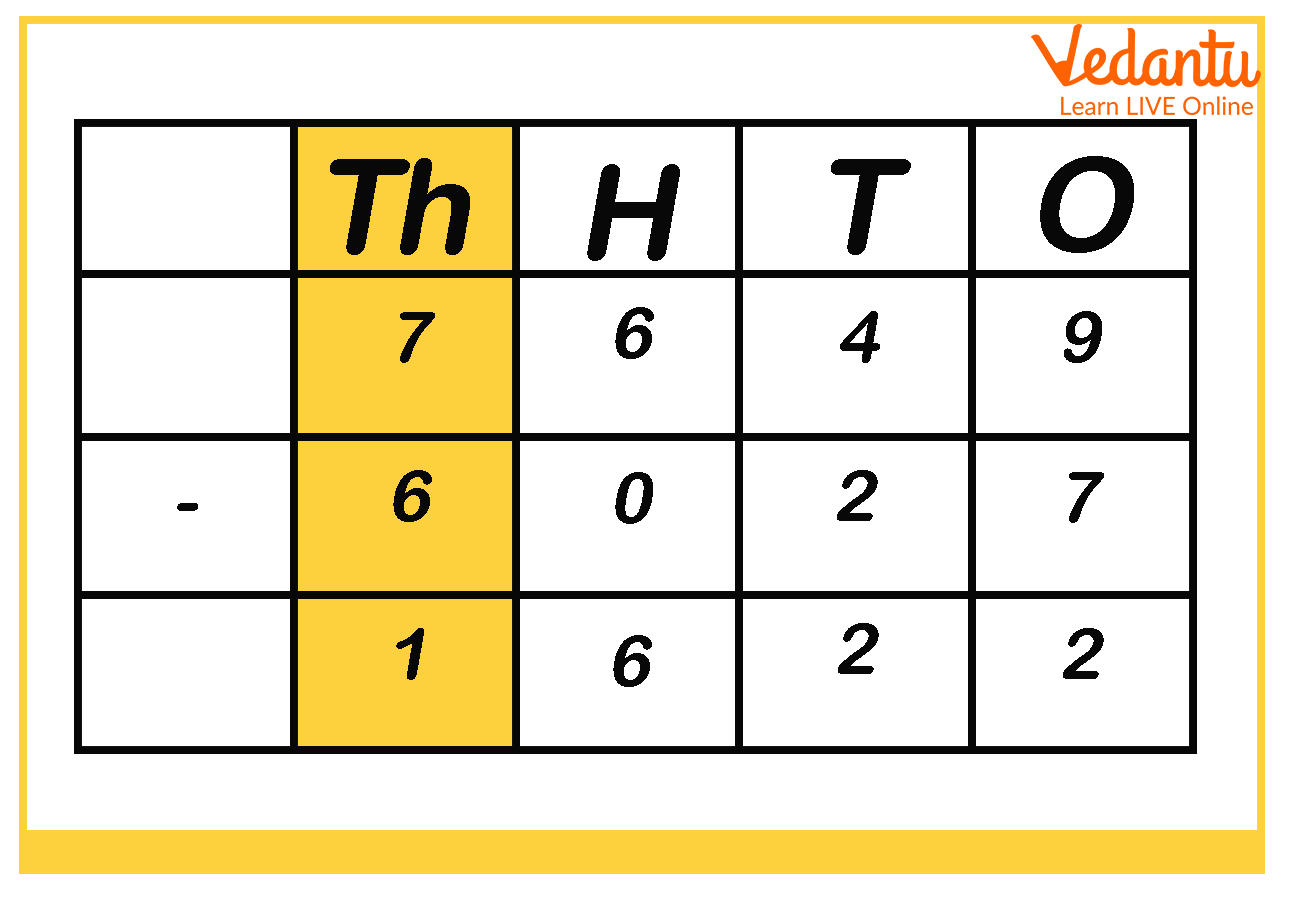
So, from the last image, we get 1622 as the result, which means subtracting 6027 from 7649 we get 1622 as the answer.
Now, let us have a look at an example of subtraction with borrowing.
Subtraction with Borrowing for Class 3 Students
We are already well-versed with borrowing on 2 and 3-digit numbers. Now, we will use the same method for subtraction of 4 and 5-digit numbers. A few examples are given below.
Example 1. Subtract 29627 from 76322.
Solution: Place the digits of the numbers according to the place value in column format as shown in the image below.
Step 1 - Subtract the digits under ones place as shown below:
Here, we can see that 2 < 7, so 1 tens is borrowed, and 1 ten + 2 ones makes it 12.
Hence, 12 - 7 = 5 ones.
Step 2 - Now, subtract the digits under tens place as shown below:
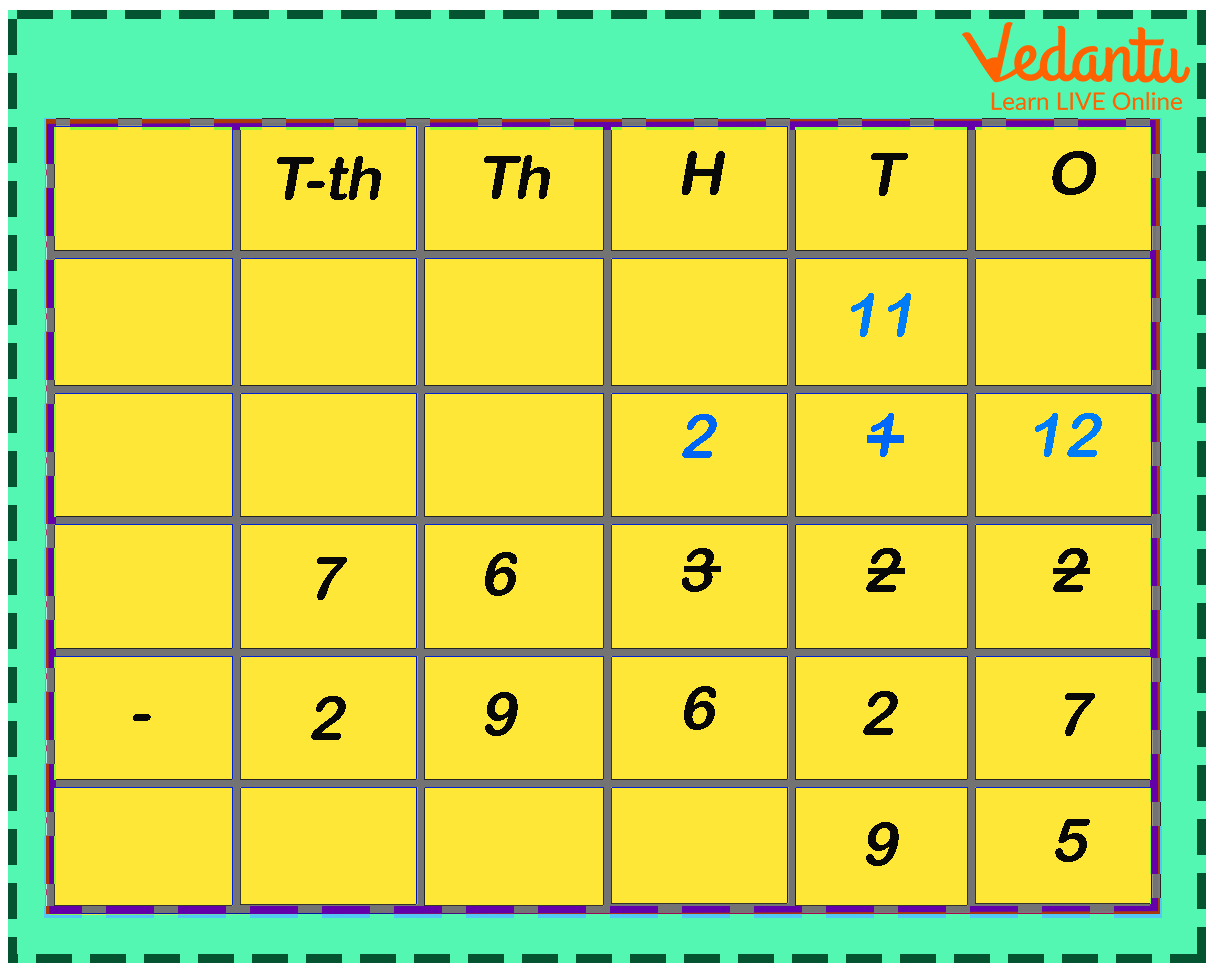
Now, 1 ten < 2 tens, so 1 hundred is borrowed and 1 hundred + 1 ten makes it 11 tens.
Hence, 11 tens - 2 tens = 9 tens.
Step 3: Subtract the digits under hundreds place.
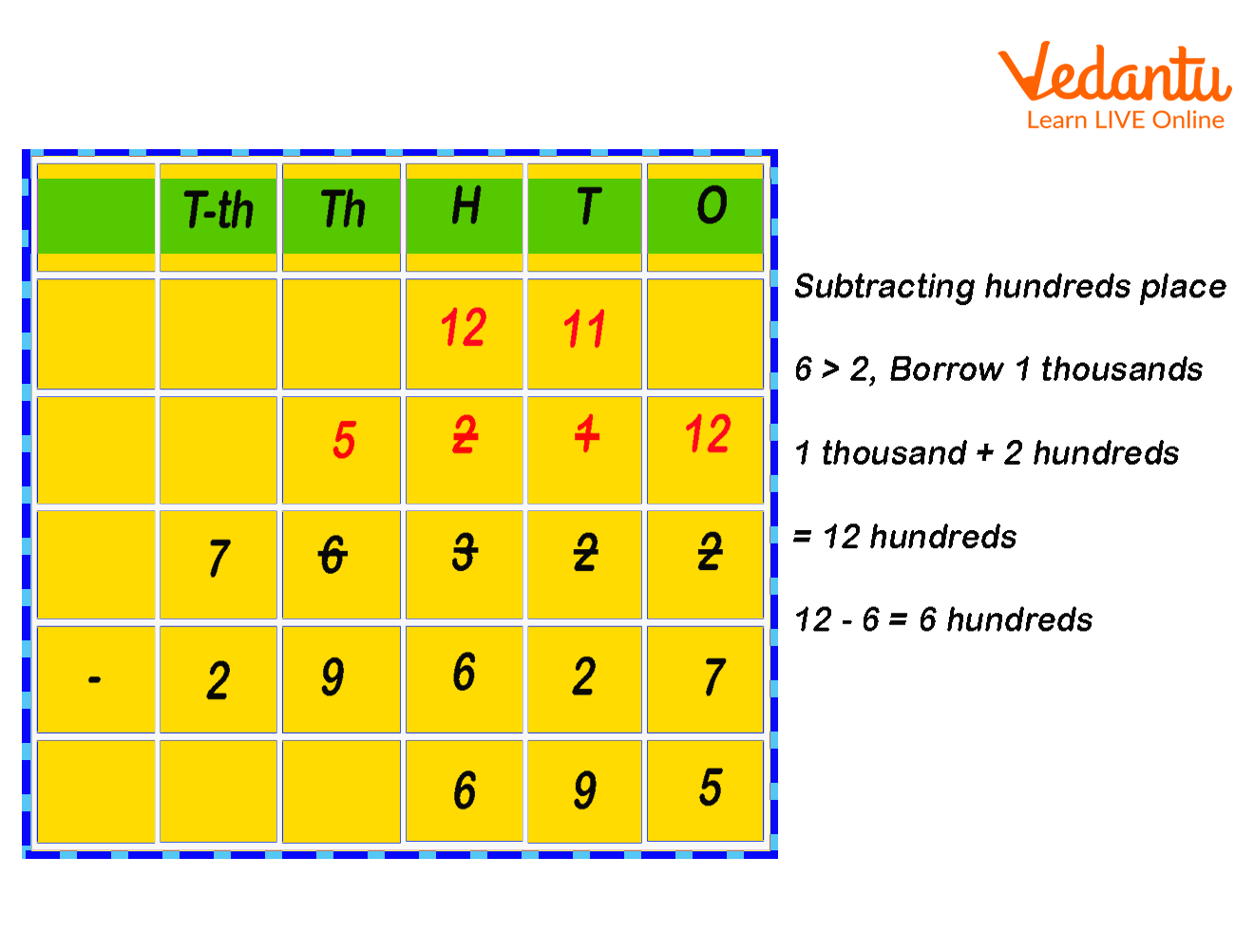
Here, 2 hundreds < 6 hundreds, so 1 thousand is borrowed and 1 thousand + 2 hundreds makes it 12 hundred.
Hence, 12 - 6 = 6 hundreds.
Step 4: Subtracting the digits under thousands place.
Here, 5 thousands < 9 thousands, so 1 ten-thousand is borrowed and 1 ten-thousand + 5 thousands makes it 15 thousands.
Hence, 15 - 9 = 6 thousands.
Now, we are left with the digit at ten-thousands place, which is 6 in place of 7, so 6 - 2 = 4.
Hence, our result by subtracting 29627 from 76322, comes out as 76322 − 29627 = 46695.
So, this is how we subtract two three-digit or four-digit numbers by using the concept of subtraction without or with borrowing along with the concept of place value.
Conclusion
Learning Maths might be troublesome for the students as well as teaching the kids Maths for the tutors or parents, in that case, gradual and baby steps introduction to the child is suggested.
In this article, we have covered the subtraction method of 3 and 4-digit numbers both by carrying and without carrying. Make your child practise the sums with different numbers and give them ample fun workbooks to complete the calculations. And in no time, you will find your child excelling in these Mathematical calculations.
FAQs on Subtraction Methods and Practice for Year 3 Students
1. What is subtraction for Year 3 kids?
Subtraction for Year 3 kids is the process of taking one number away from another to find the difference. In Year 3 Maths, children learn to subtract 2-digit and 3-digit numbers using written methods and mental strategies.
- The answer in a subtraction is called the difference.
- Example: 45 − 12 = 33.
- It helps children understand number value and place value.
2. How do you do column subtraction in Year 3?
Column subtraction is done by lining up numbers by their place value and subtracting each column starting from the ones. Follow these steps:
- Write the larger number on top.
- Line up ones under ones and tens under tens.
- Subtract from right to left.
- Regroup (borrow) if needed.
54
− 23
= 31
3. What is regrouping in subtraction?
Regrouping in subtraction means borrowing from the next place value when the top digit is smaller than the bottom digit. This is also called exchanging.
- Example: 42 − 18
- You cannot do 2 − 8, so borrow 1 ten.
- 42 becomes 3 tens and 12 ones.
- 12 − 8 = 4 and 3 − 1 = 2.
- Answer: 24.
4. What is the difference between subtraction and addition?
The difference between subtraction and addition is that addition combines numbers while subtraction takes away one number from another. For example:
- Addition: 7 + 5 = 12
- Subtraction: 12 − 5 = 7
5. How do you subtract 3-digit numbers in Year 3?
To subtract 3-digit numbers in Year 3, use column subtraction with place value (hundreds, tens, ones). Follow these steps:
- Line up hundreds, tens, and ones.
- Subtract from the ones column first.
- Regroup if needed.
356
− 124
= 232
6. What are some easy mental subtraction strategies for Year 3?
Easy mental subtraction strategies for Year 3 include counting back, partitioning, and using known facts. Common methods:
- Counting back: 15 − 3 → 14, 13, 12.
- Partitioning: 34 − 12 → (34 − 10) − 2 = 24 − 2 = 22.
- Using number bonds: 20 − 8 = 12.
7. What is the meaning of the word difference in subtraction?
In subtraction, the word difference means the answer you get when you subtract one number from another. It shows how much one number is bigger or smaller than another.
- Example: 9 − 4 = 5.
- The number 5 is the difference between 9 and 4.
8. Can you give an example of subtraction with borrowing?
An example of subtraction with borrowing is 63 − 27 = 36. Here is how it works:
- You cannot subtract 7 from 3.
- Borrow 1 ten from 6 tens (making it 5 tens).
- 13 − 7 = 6.
- 5 − 2 = 3.
- Final answer: 36.
9. Why is place value important in subtraction?
Place value is important in subtraction because it ensures digits are subtracted from the correct column (ones, tens, hundreds). Without correct place value alignment, the answer will be wrong.
- Example: In 78 − 35, subtract ones (8 − 5) and tens (7 − 3).
- Correct answer: 43.
10. What are common mistakes in Year 3 subtraction?
Common mistakes in Year 3 subtraction include not lining up place values and forgetting to regroup. Watch out for:
- Subtracting the smaller number from the larger digit without borrowing.
- Mixing up tens and ones.
- Forgetting to subtract after regrouping.
