Questions on Division

The division is a basic operation of simple Arithmetical problems. Division is a new mathematical concept. An obelus symbol (÷ or /) is used to represent the mathematical operation of division. It is another mathematical operation we use in Arithmetic problems.

In the image given below, one example is explained. In this example, 359 is divided by 6. When we divide this we get 5 remainders, 59 quotients, 6, and 359 are known as divisor and dividend respectively.

Division of 359 by 6

• Dividend: It defines the number by which we divide the given number In the problem, the dividend is 359.

• Divisor: It defines the number by which we divide the given number, where the divisor is 6.

• Quotient: This is the result that we get from the above question. In this case, it is 59.

• Remainder: This is the remaining number that is left over after the division problem, here the remainder is 5 in the given problem.

What is a Simple Division?

In Mathematics, the simple division is another method used for dividing small numbers. Simple division problems help us in dividing easy and simple division questions into divisible terms. One such example of simple division questions is given in the image  below let's have a look

Simple Division

In this example, we can see the dividend number is 42 and the divisor is 2 and the quotient is 21 and the remainder is 0. Because the dividend is totally divided by 2 so the remainder is 0.

What is the Long Division?

In the long division, we can see that there will be more and the division will look long and the remainder may be zero or may not. In calculation, long division is a system for dividing large figures into ways or corridors, breaking the division problem into a sequence of easier ways. It's the most common system used to break problems grounded on division.

Long Division Steps

To perform division requires the construction of a tableau. The divisor is separated from the tip by a right gap 〈) 〉 or perpendicular bar 〈| 〉 and the tip is separated from the quotient by a vinculum( an overbar). Now, let us follow the way of the long division given below to understand the process.

• Step 1 - Take the first number of the tip from the left-wing. Check if this number is lesser than or equal to the divisor.

• Step 2 - Also divide it by the divisor and write the answer on top as the quotient.

• Step 3 - Abate the result from the number and write the difference below.

• Step 4 - Bring down the coming number of the tip( if present).

• Step 5 - Repeat the same process.

Example:

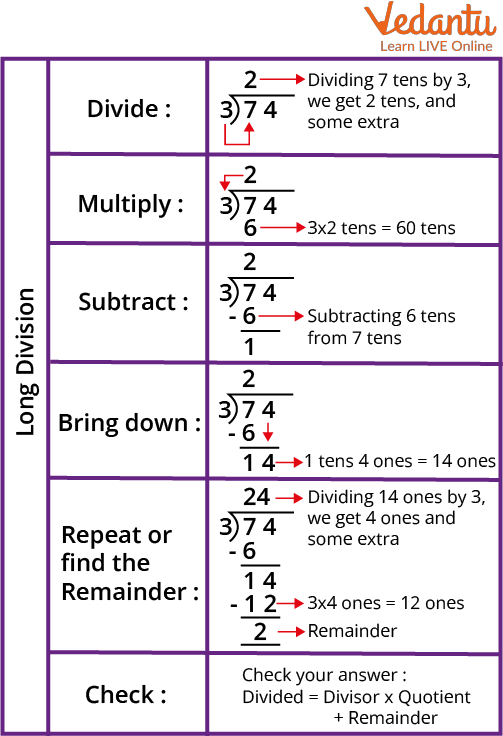
Steps Involved in Long Division

Solved Examples

1. Find the value of quotient and remainder when 23 is divided by 2? Verify using the Long division method.

Ans. Here we divided 23 by 2 so the dividend is 23 and the divisor is 2.

Long division

In this example, we can see 23 as a dividend and 2 as a divisor. It is not divisible by 2 directly; it took more steps to become divisible and get 1 as a remainder.

2. Find the value of quotient and remainder when 75 is divided by 3? Verify using the Long division method.

Ans. Here we divided 75 by 3 so the dividend is 75 divisor is 3

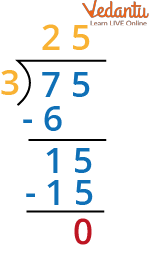
Division of 75 by 3

Hence, we get the quotient is 25 and the remainder as 0

To check division we will put the value.

Dividend = (Divisor × Quotient) + Remainder. 

Therefore, 75 = 3 × 25 + 0 = 75

Division Practice Questions:

1. 228 seats must be occupied in an auditorium. If there are seven rows overall, how numerous chairpersons are needed in each row? How many redundant chairpersons are there?

Ans. If there are seven rows overall 32, 4

2. Divide 882 by 9. 

Ans. 98

Summary

Following are the points that need to be remembered while studying this topic:

• In the case of whole figures, the tip is always lesser than or equal to the divisor and the quotient.

• The remainder is always lower than the divisor.

• For division, the divisor can not be 0.

• The division is repeated deduction, so we can check our quotient by repeated deductions as well.

• We can corroborate the quotient and the remainder of the division using the division formula tip = ( Divisor × Quotient) Remainder.

• Still, also we can check our quotient by multiplying it with the divisor, If the remainder is 0. still, also the quotient is correct, If the product is equal to the tip.