




Key Quadrilateral Concepts, Properties, and Solved Examples
Introduction to Quadrilateral
When we see a tabletop or a handkerchief, the basic quadrilateral shapes—a rectangle or a square—come to mind. There are many numerous varieties of quadrilaterals, and the shapes of the quadrilaterals themselves can recognize the types of quadrilaterals. The word is made up of two Latin words, Quadri, which is a variation of four, and latus, which signifies sides, as suggested by the name. A quadrilateral is a two-dimensional polygon with four sides. Quadrilaterals include the following 2D shapes: square, rectangle, rhombus, trapezium, parallelogram, and kite.

Quadrilaterals
Definition of Quadrilaterals
A quadrilateral is a form of a polygon that consists of four sides, four vertices, four angles, and two diagonals.
Properties of Quadrilaterals
The properties of a quadrilateral set it apart from a normal polygon in various ways. We have listed some common properties of quadrilaterals below:
They must have four sides.
They must have four vertices.
They must have two diagonals.
360° is the total sum of interior angles.
Quadrilateral shapes explain a lot about their properties.
Types of Quadrilaterals
There are various types of quadrilaterals, depending on different characteristics, and unique shapes. Just by looking at the quadrilateral shapes, one can tell the differences and qualities between them. Let's briefly discuss some of the types of quadrilaterals in this section.
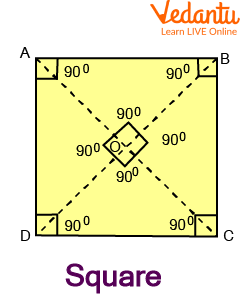
Square: A quadrilateral with four equal sides and angles is called a square. The fact is that its sides and angles are equal, making it a regular quadrilateral. A square has four 90° angles. It can alternatively be viewed as a rectangle with equal lengths on its two neighbouring edges.
Square
Sides: $A B=C D$ and $B C=A D$
Diagonals: $\mathrm{AO}=\mathrm{OC}$ and $\mathrm{DO}=\mathrm{OB}$
Angles: $\angle A=\angle C$ and $\angle B=\angle D=90^{\circ}$
If a square's side is "a," then
The square's area is equal to $a\times a =a^{2}$
The Square's perimeter is equal to 4a.
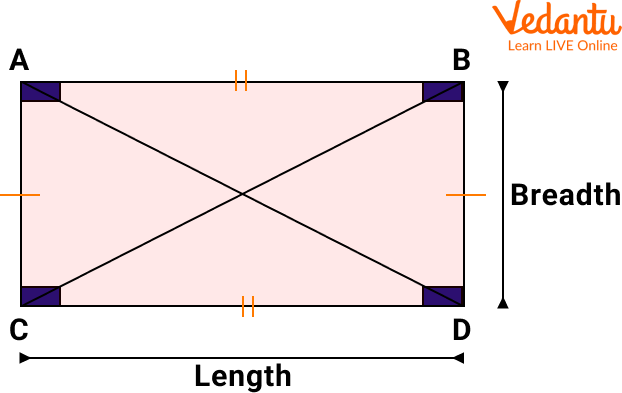
Rectangle: A rectangle contains four corners and four sides where opposite sides are of the same length and parallel to each other. The angles of a rectangle are equal in measure and are right-angled i.e. they measure $90^{\circ}$.
Rectangle
Some of the properties of the rectangle are given below:
Two pairs of parallel sides.
All four angles are right angles, that is, they measure 90 degrees.
Opposite sides are of equal lengths.
Two equal diagonals
In a rectangle, the two diagonals bisect each other in equal halves In the rectangle $P Q R S, P Q\|R S, P Q=R S, P S\| Q R$, and $P S=Q R$. All the angles are $90^{\circ}$ angles.
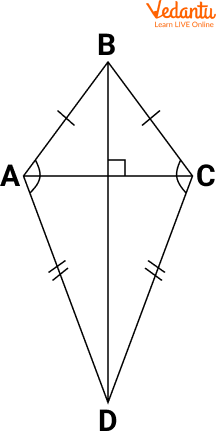
Kite: A kite has various names such as a dart or an arrowhead because of the shape. A kite has two pairs of equal-length sides and these sides are adjacent to each other.
Some of the properties of the kite are given below:
Contains four edges and four vertices.
Contains one line of symmetry.
Contains two pairs of congruent and consecutive sides.
Diagonals are perpendicular to each other.
In the kite $P Q R S, P Q=Q R$, and $P S=S R$.
Kite
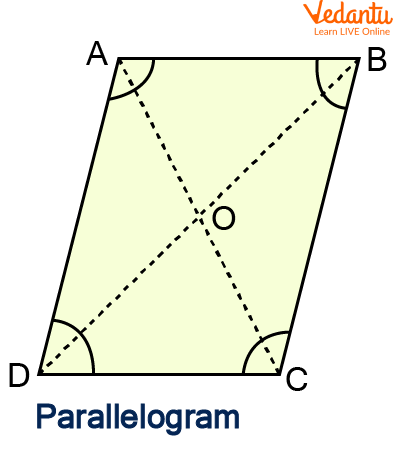
Parallelogram: As the name implies, a parallelogram is a simple quadrilateral with opposite sides as parallel. It, therefore, has two sets of parallel sides. A parallelogram also has its opposite angles as equal. In addition, the diagonals of a parallelogram cut each other. The sum of any two adjacent angles equals 180°.
Parallelogram
Sides: $A B=C D$ and $B C=A D$
Diagonals: $\mathrm{AO}=\mathrm{OC}$ and $\mathrm{DO}=\mathrm{OB}$
Angles: $\angle A=\angle C$ and $\angle B=\angle D$
If a parallelogram's length is I, breadth is $b$, and height is $h$, then
Parallelogram's perimeter equals $2 \times(\mathrm{l}+\mathrm{b})$.
Parallelogram's area equals $\mathrm{l} \times \mathrm{h}$
Rhombus: A quadrilateral called rhombus has four equal sides that are non-parallel to one another. The angles are not exactly 90 degrees. Right angles transform a rhombus into a square. In recognition of its similarities to the diamond card of playing cards, the rhombus is sometimes known as the "diamond."
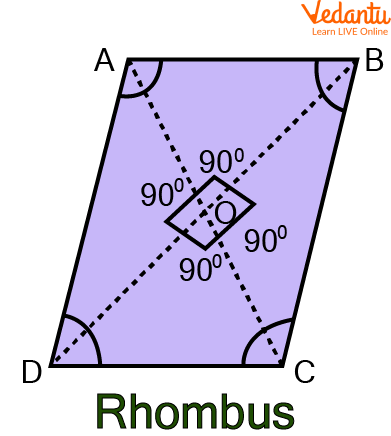
Rhombus
Sides: $A B=C D$ and $B C=A D$
Diagonals: $\mathrm{AO}=\mathrm{OC}$ and $\mathrm{DO}=\mathrm{OB}$
Angles: $\angle A=\angle C$ and $\angle B=\angle D$
A rhombus's perimeter is equal to 4a if its side is a.
If two of the rhombus' diagonals are $d_{1}$ and $d_{2}$, then the area of a rhombus is equal to $\dfrac{1}{2} \times d_{1} \times d_{2}$
Trapezium: One pair of parallel sides make up a quadrilateral known as a trapezium. The two other sides are referred to as "legs" or "lateral sides," whereas the parallel sides are known as "bases."
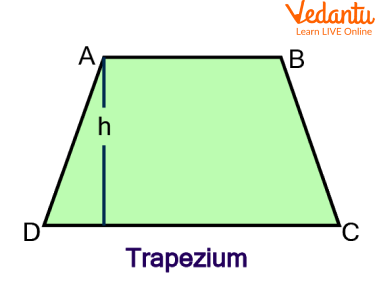
Trapezium
As demonstrated in the diagram above, if a trapezium's height is "h," then
Trapezium perimeter = total lengths of all sides, which are AB + BC + CD + DA.
The area of the trapezium equals $\dfrac{1}{2} \times (AB + CD) \times h$
Quadrilateral Solved Problems
Q1. Find the base of a parallelogram, if its area is 144 square units and the height is 6 units.
Ans: Given, a parallelogram with;
Area = 144 square units
Height = 6 units
Therefore the area of the parallelogram = Base × Height
144 = Base $\times$ 6
Base = $\dfrac{114}{6}$ = 24 units
Q2. Calculate the quadrilateral's perimeter, which has sides of 2, 4, 9, and 15 cm.
Ans: We have the sides of a quadrilateral: 2 cm, 4 cm, 9 cm and 15 cm.
Therefore, the perimeter of a quadrilateral is given by the sum of all its sides, i.e.
P = 2 cm + 4 cm + 9 cm + 15 cm
P = 30 cm
Q 3. Find the missing angle x.
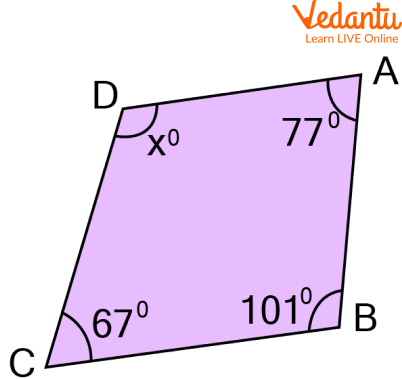
Quadrilateral
Ans: We are aware that in a quadrilateral, the sum of all the angles is equal to $360^{\circ}$.
Therefore, we can express it as follows:
$x+77^{\circ}+101^{\circ}+67=360^{\circ}$
$x+245^{\circ}=360^{\circ}$
$x=360^{\circ}-245^{\circ}$
Hence, $x=115^{\circ}$.
Quadrilateral Practice Problems
Q1. The quadrilateral has three sides that measure 9 cm, 13 cm, and 17 cm in length, and its perimeter is 50 cm. Find the quadrilateral's missing side.
Ans: 11 cm.
Q 2. Find $\angle B C D$, if the figure at left, $\mathrm{ABCD}$ is a cyclic quadrilateral in which $\mathrm{AB} \| \mathrm{DC}$. If $\angle \mathrm{BAD}= 100^{\circ}$
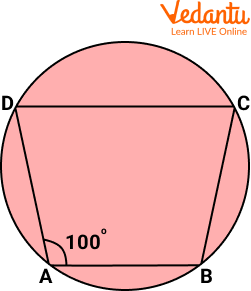
ABCD is a cyclic quadrilateral
Ans: $80^{\circ}$
Summary
Let us summarise what we have learned throughout this article. A quadrilateral is a polygon with four sides and four angles, such as a square, parallelogram, rectangle, trapezium, kite or rhombus. There are various types of quadrilaterals, depending on different characteristics, and shapes. The properties of quadrilaterals, namely square, parallelogram, rhombus, and trapezium are discussed, along with their solved examples, in brief in the above article. Try out the given practice questions to get a better understanding of the topic, quadrilateral.
FAQs on Quadrilateral Practice Problems for Exam Success
1. What are the most frequently asked types of questions from the Quadrilaterals chapter in CBSE exams?
For the CBSE 2025-26 exams, students should focus on a few key types of questions from Quadrilaterals. These typically include:
- Proof-based questions involving properties of parallelograms, rhombuses, rectangles, and squares.
- Problems based on the Mid-point Theorem and its converse.
- Calculation questions where angles of a quadrilateral are given in a ratio.
- Higher Order Thinking Skills (HOTS) questions that require proving a figure is a specific type of quadrilateral given certain conditions.
2. How do you solve a problem where the angles of a quadrilateral are in a given ratio, for example, 3:5:9:13?
This is a classic exam problem. To solve it, follow these steps:
1. Let the angles be 3x, 5x, 9x, and 13x.
2. Use the Angle Sum Property of a Quadrilateral, which states that the sum of all interior angles is 360°.
3. Set up the equation: 3x + 5x + 9x + 13x = 360°.
4. Solve for x: 30x = 360°, which gives x = 12°.
5. Calculate each angle by substituting the value of x. The angles would be 3(12) = 36°, 5(12) = 60°, 9(12) = 108°, and 13(12) = 156°.
3. What is the Mid-point Theorem and what kind of exam questions are based on it?
The Mid-point Theorem states that the line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is half of its length. Exam questions often require you to apply this theorem to prove properties of quadrilaterals. For instance, a common important question is to prove that the quadrilateral formed by joining the mid-points of the sides of another quadrilateral is a parallelogram.
4. What are the minimum conditions you need to prove in an exam to show that a quadrilateral is a parallelogram?
To prove a quadrilateral is a parallelogram, you do not need to prove all its properties. Proving any one of the following conditions is sufficient for full marks:
- Show that both pairs of opposite sides are parallel.
- Show that both pairs of opposite sides are equal in length.
- Show that one pair of opposite sides is both equal and parallel.
- Show that the diagonals bisect each other.
- Show that both pairs of opposite angles are equal.
5. How do the properties of diagonals help distinguish between a square, rhombus, and rectangle in a proof-based question?
The properties of diagonals are crucial for distinguishing these figures, which is a common point of confusion. Here's how to use them in a proof:
- If the diagonals of a parallelogram are equal, it is a rectangle.
- If the diagonals of a parallelogram bisect each other at right angles (90°), it is a rhombus.
- If the diagonals are both equal and bisect each other at right angles, it is a square.
6. What is a common mistake students make when trying to prove a quadrilateral is a rhombus?
A very common mistake is proving that the diagonals are perpendicular bisectors but forgetting to first prove that the figure is a parallelogram. The property that perpendicular diagonals make a rhombus is only true if the quadrilateral is already known to be a parallelogram. To avoid losing marks, your proof must first establish that the shape is a parallelogram, and then show the diagonal property.
7. Why is it necessary to understand the properties of different quadrilaterals for solving complex geometry problems?
Understanding the specific properties of each quadrilateral (like parallelograms, trapeziums, kites) is essential because complex problems often involve composite figures. A larger shape might be composed of a triangle and a trapezium, or you might need to prove a property by constructing a specific type of quadrilateral within a figure. Knowing that a rhombus has equal sides or that a rectangle's diagonals are equal allows you to unlock steps in a proof that would otherwise be impossible.
8. In a typical 5-mark question, how would you prove that the bisectors of the angles of a parallelogram form a rectangle?
This is a high-value exam question. The key steps are:
1. Draw a parallelogram ABCD and the bisectors of angles A, B, C, and D, which intersect to form a new quadrilateral PQRS.
2. Use the property that consecutive angles of a parallelogram are supplementary (sum to 180°). For example, ∠A + ∠B = 180°.
3. Consider the triangle formed by two vertices and the intersection of their angle bisectors (e.g., ΔAPB). Show that the sum of the base angles (1/2 ∠A + 1/2 ∠B) is 90°.
4. This proves that the third angle in the triangle (∠APB) is 90°.
5. Since ∠SPQ is vertically opposite to ∠APB, ∠SPQ = 90°. By repeating this for all vertices, you can prove that all angles of PQRS are 90°, making it a rectangle.

















