Progressive Pattern

A pattern is something that repeats itself. It can be a man-made object or something occurring naturally in nature, like the petals of sunflowers. You can see patterns in the way things are arranged in your kitchen; you can see patterns in how streetlights are placed. Therefore, patterns are everywhere. Some patterns repeat while others grow or develop. There are various types of patterns in math as well. However, today we will learn about the progressive pattern. The pattern created by either increasing or decreasing is known as a progressive pattern.

What is a Progressive Pattern?

Progressive patterns are those that either increase or decrease in two or more different ways. They are a combination of more than one change. If you have ever been to the doctor who checks your eyes, you must have seen some patterns on the screen. Have a look at the image below. The chart you see is the one the doctors use to check your eyes. These are called log MAR charts.

You can see how it continuously decreases in size. This decreasing pattern is the best example of a progressive pattern. Examples of progressive patterns in math include geometric progressions, arithmetic progressions, etc., which you will learn in higher classes.

Log MAR charts used by Ophthalmologists

How to Identify the Pattern Type?

You now understand what a progressive pattern is. You can do this by marking the difference between the first two numbers/pictures and between the second and third numbers/pictures. It will form a progressive pattern when comparing whether the difference increases or decreases. Notice how the difference keeps increasing by 1.

Progressive pattern

Questions Related to the Number Pattern

1. Fill in the blanks with the correct numbers

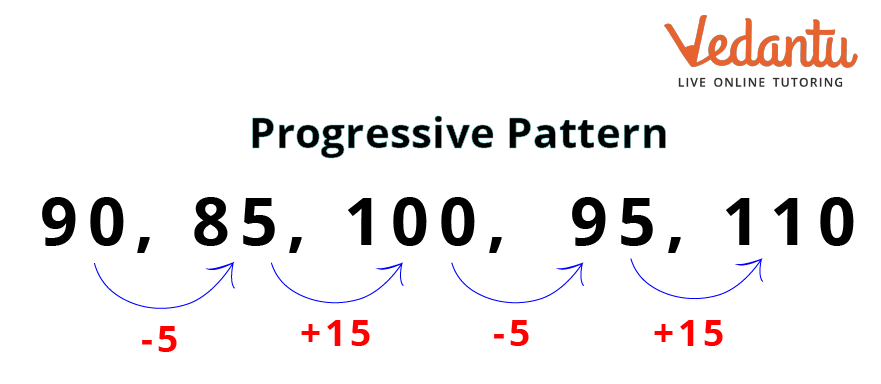
i. 90, 85, 100, 95, 110, _, _

In this question, observe the difference between the first two numbers.

$90-85=5$

The difference is 15.

Take the second and third numbers now.

$85 + 15 = 100$

The difference between 85 and 100 is 15.

Let us take 100 and 95 now.

$100 - 95 = 5$

The difference is 5. 

The difference was at first 5, then increased to 15, then again decreased to 5.

Let’s take 95 and 110 now.

$95 + 15 = 110$

The pattern the numbers follow is -5, +15, -5 and +15. 

So, if the pattern is followed, the next number will be $110-5=105$.

The next number will again follow the pattern, which is +15.

Hence, $105 + 15 = 120$.

The answers are 105 and 120.

ii. 160, 110, 70, ___, ___

Observe the difference between 160 and 110. 

$160 - 110 = 50$

The difference is 50.

Let's observe the second and third numbers now. 

$110 - 70 = 40$

You can see that the difference keeps decreasing by 10. 

So, this way, the following number will be $70 - 30 = 40$ .

The number next to 40 will be $40 - 20 = 20$.

Hence, the numbers are 40 and 20.

2. Identify the pattern type.

Progressive pattern question

Answer: Progressive pattern

You can see that the circles keep getting larger as you move down the pattern. This is purely a progressive pattern, as the difference between each row keeps growing by 1.

Conclusion

Today, you have learnt about patterns, specifically progressive patterns, along with some real-life examples. Apart from that, you have also learnt to identify progressive patterns by observing the difference between two consecutive numbers or images. You have also practised a few questions related to the progressive pattern.