Plane Figures and Solid Shapes

A plane figure is a geometric shape. A plane figure is known as a 2-dimensional shape because it has only length and breadth. The thickness of the plane figure is zero. Any shape that is drawn on paper is known as a plane figure. In the real world, there is no object that represents a plane figure.

Define Plane

A plane is a two-dimensional surface measured by two linearly independent points; a plane doesn't have an obvious direction and can extend indefinitely. In algebra, the points are plotted in the coordinate plane which has a number line extending left to right and upwards and downwards endlessly and infinitely. Two planes can be parallel to each other, can be identical and can intersect each other. A plane has nothing but a surface with no thickness or width. It is always two dimensional. Imagine a wall and extend it infinitely, it becomes a plane.

Plane Figures and Shapes

Plane figures include squares, rectangles, triangles, circles, pentagons, octogen, hexagons, ovals etc. A grouping of shapes is called polygons, like squares and rectangles, but circles and ovals are not polygons.

In contrast to solid shapes, a closed two-dimensional or flat surface figure is known as a plane shape. Instead of edges and faces, they possess several light lines that make a corner or a vertex where the two straight lines meet. Some basic plane shapes are triangles, squares, rectangles, circles and ovals. If we closely observe a sheet of paper, our observation would be on its length and width but no depth, so they are closed shapes as they are made by joining either two straight lines or curved lines. They are also known as plane geometric figures or polygons.

Examples of Plane Shapes

Plane shapes include squares, rectangles, triangles, circles, pentagons, octagons, hexagons, ovals etc.

Triangle: A polygon with three sides and three angles is known as a triangle.

Triangle

Quadrilateral: A closed polygon bounded by four sides is known as a quadrilateral.

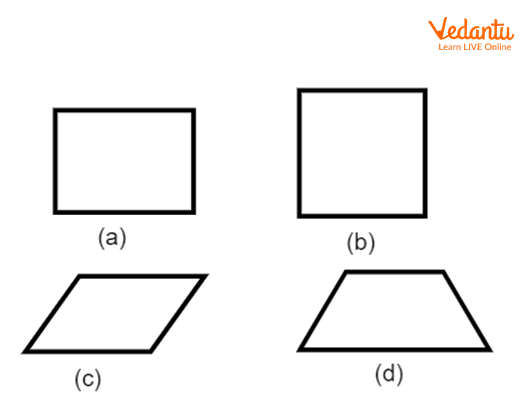
Types of Quadrilateral

Circle: If all points in the figure are equidistant from a fixed point, then it is known as a circle. The fixed point is known as the centre of the circle.

Circle

Pentagon: If a shape is bounded by 5 sides, then it is known as a pentagon.

Pentagon

Hexagon: If a shape is bounded by 6 sides, then it is known as a hexagon.

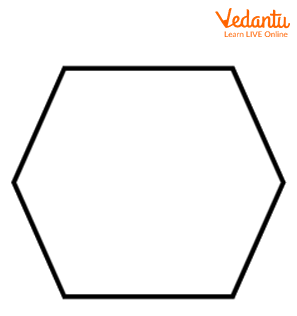
Hexagon

What are Solid Shapes?

Shapes that can be seen and measured from three dimensions are called solids. Length, width and height which can also be thickness or depth are what define solid shapes. A two-dimensional shape can be folded to form a 3D shape, when it is laid out flat showing each face, the pattern is called a net. So, a net is an unfolded form of a 3D figure. Three major properties of solid shapes are faces, vertices and edges.

Solid Shapes Examples

Examples of solid shapes include cubes, cuboids, pyramids, prisms, cylinders, spheres, cones, torus, trapezoid, rhombus, parallelograms and quadrilaterals. It can be a combination of two or more actual figures: a pen is a combination of two cylinders, and a dome is made up of a hemisphere on a cylinder or a cone.

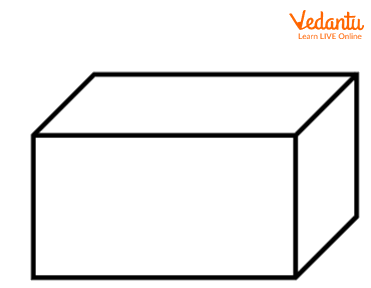
Cuboid

The real-life examples of cuboids are brick, tiffin boxes, books, matchboxes etc.

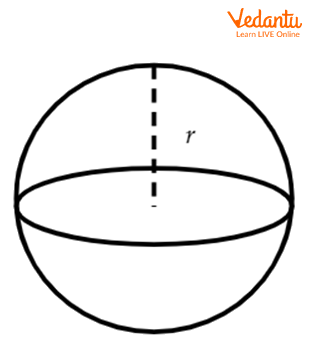
Sphere

The real-life examples of spheres are globes, marble, orange, bubbles etc.

Cone

The real-life examples of cones are ice cream cones, traffic cones, birthday caps etc.

Difference Between Solid and Plane Figure

Interesting Facts

• A tessellation is created when a particular shape is repeatedly made without any overlapping or gaps and it covers a plane. Only rectangular hexagons, equilateral triangles and squares can make regular tessellations.

• The hexagonal cells in a honeycomb or diamond shape pattern on a snakeskin are natural examples of tessellation.

Solved Examples

1. What is the surface area of a cube whose length of a side is 6 cm?

Ans: The surface area of a cube is $$6a^2$$.

The area of the surface area is $$6\times 6^2=216{\text{ cm}}^2$$.

2. If the radius of a circle is 7 cm, then what is the area of the circle?

Ans: The area of a circle is$$\pi r^2$$.

The area of a circle is $$\pi 7^2={\displaystyle \frac{22}{7}}\times 7^2=154{\text{ cm}}^2$$.

Key Features

• A plane is a two-dimensional surface measured by two linearly independent points.

• Plane figures include squares, rectangles, triangles, circles, pentagons, octogen, hexagons, ovals etc.

• A closed two-dimensional or flat surface figure is known as a plane shape.

Practice Question

Question. If the area of a square is equal to the area of a circle, what is the ratio of the square of the length of the square to the square of the radius of the circle?

Answer: $$\pi$$.