Hexagon - Angles, Diagonals, Properties, Area, and Perimeter
What is a Hexagon?
A hexagon is a 2D geometric figure enclosed by six straight edges. In the below-given picture, you can see that the six edges of a hexagon make six vertices and six angles. Are you wondering why this shape is termed hexagon? Well, a six-sided polygon is termed a hexagon as “hex” stands for six and “gonia” stands for corners. Hexagons can be broadly classified as regular hexagons and irregular hexagons on the basis of the length of their sides. Also, hexagons can be classified into convex and concave on the basis of the measure of their angles.
Now, let us learn about the angles, diagonals, formulas, and properties of hexagons in detail.
A Hexagon
Can we Find the Hexagon Pattern Around Us?
The hexagon shape can be found in various objects around us, for example, a honeycomb. Have you ever noticed a honeycomb? Well, let us take a closer look at the below-given picture. Each little unit in a honeycomb has six sides, making it a hexagon.
Each little unit of a honeycomb resembles a hexagon shape
We can find the shape of a hexagon in a floor tile, on a clock, on hexagonal specs, on the cross-section of a pencil, etc.
Hexagonal pencil surface
What is a Regular Hexagon?
When the lengths of all hexagonal sides are equal, it is known as a regular hexagon. Also, the angles of a regular hexagon are equal. Interestingly, a regular hexagon can be divided into six equilateral triangles.
A regular hexagon divided into six equilateral triangles
What is an Irregular Hexagon?
When the sides of a hexagon are unequal in length, it is known as an irregular hexagon. The angles of an irregular hexagon are not equal. An irregular hexagon cannot be divided into six equilateral triangles.
An irregular hexagon
Convex and Concave Hexagons
Each vertex of a convex hexagon is pointed outwards, and all interior angles are less than 1800. The sides of a convex hexagon can be equal or unequal.
In a concave hexagon, one or more interior angles measure greater than 1800. Also, one or more vertex points inwards in a concave hexagon.
Convex and Concave hexagons
Sides and Angles of a Hexagon
As stated above, a hexagon, regular or irregular, has six sides. The hexagon sides are straight, forming closed 2-D shapes. Adding up the lengths of all sides of a hexagon gives its perimeter. If the perimeter of a regular hexagon is given, the length of its every side can be determined by dividing the perimeter by 6.
Length of each side of a regular hexagon = Perimeter/6
However, the same is not applicable for an irregular hexagon. Since two or more sides of an irregular hexagon are unequal, the length of its sides cannot be determined from its perimeter.
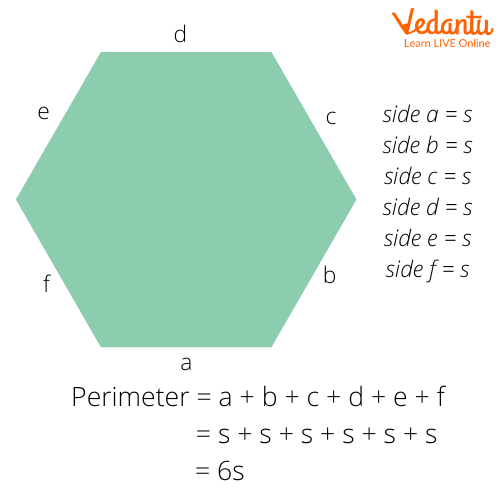
Perimeter of a regular hexagon
A hexagon has 6 interior angles and 6 exterior angles. The sum of the interior angles of a hexagon is 7200. As the interior angles of a regular hexagon are equal, the measure of each can be determined as 7200/6. Therefore, each interior angle of a regular hexagon measures 1200.
The sum of the exterior angles of a hexagon is 3600. Each exterior angle of a regular hexagon can be determined as 3600/6. Therefore, each exterior angle of a regular hexagon measures 600.
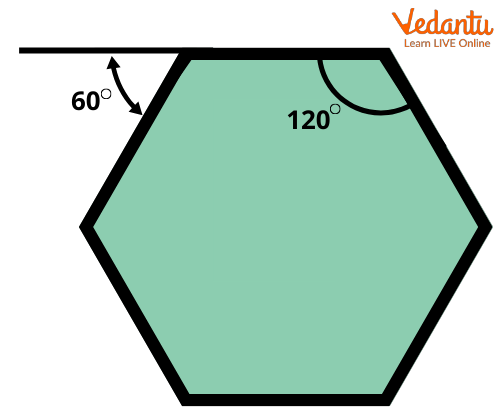
Interior and exterior angles of a regular hexagon
Diagonals of Hexagons
A line segment connecting any two non-adjacent vertices of a hexagon is referred to as the diagonal of the hexagon.
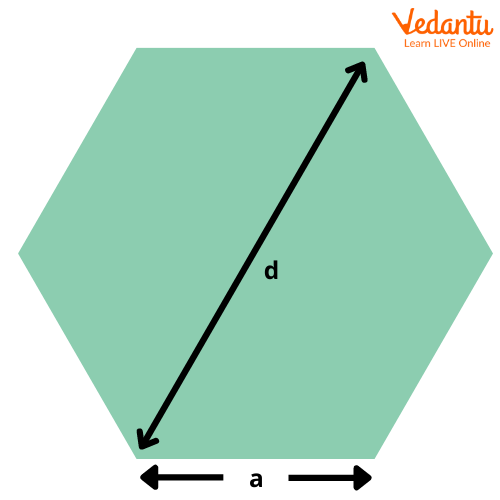
A diagonal of a regular hexagon
A hexagon has 9 diagonals connecting its non-adjacent vertices. Of these, 3 diagonals pass through the centre of the hexagon. The diagonals of a hexagon can be classified as long diagonals and short diagonals. The 3 diagonals of a hexagon that pass through its centre happen to be greater in length than the rest of the diagonals. Hence, these are referred to as the long diagonals.
Length of a long diagonal of a regular hexagon = 2 x length of each side of the hexagon.
The 6 diagonals of a hexagon that do not pass through its centre are referred to as the short diagonals.
Length of a short diagonal of a regular hexagon = 3 x length of each side of the hexagon.
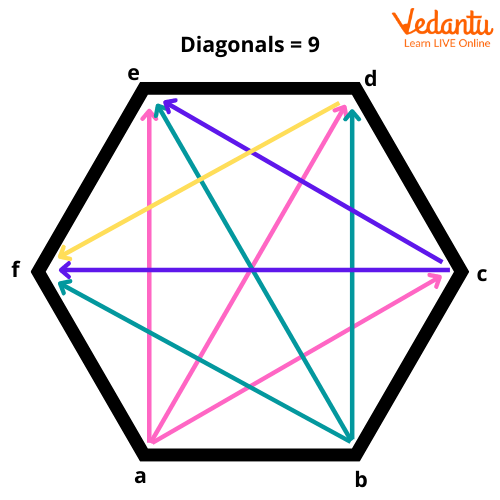
Regular Hexagon Diagonals
Properties of Hexagons
There are different types of hexagons, each with a definite set of properties. Some hexagons may have equal sides, whereas some may have their vertices pointing inwards. So, let us sum up the basic properties of hexagons in general.
A hexagon (“hex”: six and “gonia”: corners) has 6 sides, 6 angles, and 6 vertices.
A regular hexagon is symmetrical.
The opposite sides of a regular hexagon run parallel to each other.
The sides of regular hexagons have the same lengths.
The sum of the interior angles of all hexagons is 7200.
The sum of the exterior angles of all hexagons is 3600.
There are 9 diagonals, 3 long and 6 short, in a regular hexagon.
All regular hexagons are convex.
Some irregular hexagons are concave.
Area and Perimeter of Regular Hexagons
As a regular hexagon can be divided into 6 equilateral triangles, the area of a regular hexagon is calculated by the following formula:
Area: 3 \[ \frac{\sqrt{3}}{2} \] a2
(where \[ \frac{\sqrt{3}}{2} \] a2 is the area of an equilateral triangle and a is the length of each side of the hexagon)
The perimeter of a hexagon can be calculated by adding the lengths of all sides of the hexagon. As the sides of a regular hexagon are equal in length, its perimeter can be calculated by the following formula:
Perimeter = 6a
(where a is the length of each side of the hexagon)
Solved Examples
The below-given examples will help you to understand the application of the above-given formulas of area and perimeter of hexagons.
Each side of a regular hexagon is equal to 5 cm. Find its perimeter and area correct up to two decimal places.
Solution:
Length of each side of the regular hexagon = 5 cm
{ Since perimeter of hexagon= 6a }
Therefore, the perimeter of the hexagon = (6 x 5) cm
= 30 cm
{ Since Area of a hexagon= \[ \frac{\sqrt{3}}{2} \] a2}
The area of the hexagon = \[ \frac{\sqrt{3}}{2} \] 52 cm2
= 64.95 cm2
The perimeter of a hexagonal field is 96 metres. Find its area correct up to two decimal places.
Solution:
The perimeter of the field = 96 m
{Since perimeter of hexagon= 6a }
Therefore, the length of each side of the hexagonal field = 96/6 m
=16 m
Therefore, the area of the field = \[ \frac{\sqrt{3}}{2} \] 162 m2
= 665.11 m2
Hexagons form one of the most fundamental concepts of geometry. With practice, kids develop a thorough understanding of the properties of hexagons. Most kids enjoy the hexagon drawing or construction, with given hexagon angles and sides, as they get a better insight of this polygon during the activity. So, encourage your kids to solve various interactive worksheets and activities on hexagons for a seamless learning experience.
FAQs on Hexagon
1. What is a convex hexagon?
If all the vertices of a given hexagon point in the outward direction, it is referred to as a convex hexagon. The regular hexagons have all the vertices pointing outward, hence they are convex hexagons. Also, some irregular hexagons that do not have equal sides can be convex.
2. How many diagonals are there in a regular hexagon?
There are a total of 9 diagonals in a regular hexagon. The lengths of the diagonals are not equal and three diagonals are longer than the rest. These are called the long diagonals of a regular hexagon and run through its centre. The other six diagonals of the regular hexagon are called its short diagonals.
