Understanding Operation on Fractions

A fraction is a part of either complete or whole. We can say that a fraction is the number of equal parts taken from a whole. A circle is the combination of 4 quadrants. Therefore, we can say quadrants are known as parts whereas a circle is known as a whole.

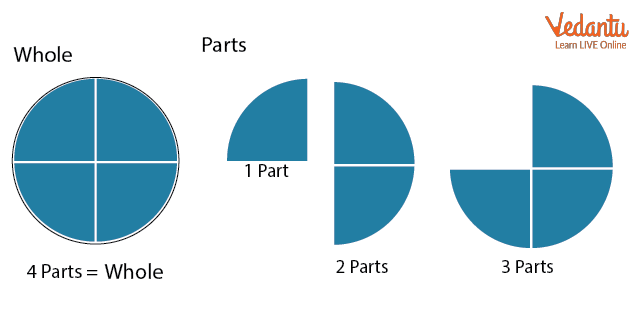
Let’s understand with the help of a few examples:

1. Your dad ordered a pizza (4 slices) from a shop. If I ask you what the whole part is then you can say that the full-size pizza (4 slices) is whole.

Now, your dad distributed slices between you and your 3 cousins. You got one slice of pizza.

Now, if I ask you how many slices of pizza you get from a complete pizza then your answer should be 1 slice out of 4 slices. So, this 1 out of 4 will be known as a fraction of the whole pizza

2. You might have seen the National flag of India, but if I ask you how many strips are saffron coloured then what will come to your mind?

You will think of the whole flag as having 3 strips: saffron, white and green. So, one strip out of 3 strips is coloured as saffron. So now you can say that the whole flag consists of  3 strips and a part of the whole is one strip. 

Representation of Fractions

In mathematical terms, the part of the whole is known as the numerator of the fraction, and the whole is known as the denominator of the fraction. 

In the above-mentioned example, if you got 3 slices of pizza then that is the numerator and the total number of slices in pizza (4) will be the denominator of the fraction. So fraction will be written as: 

Fraction = $\dfrac{Numerator}{Denominator}=\dfrac{3}{4}$

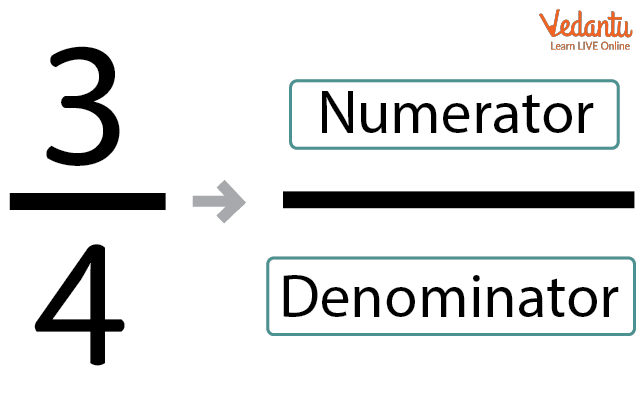
The below image explains more about fraction representation.

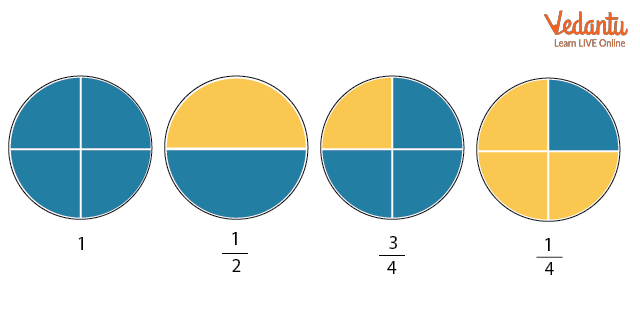
Addition of Fractions

If I ask you to add $\dfrac{1}{4}+\dfrac{2}{4}$ then how will you do it?

Let’s imagine a pizza with a total of 4 slices. Here $\dfrac{1}{4}$ represents 1 slice out of 4 slices and $\dfrac{2}{4}$ represents 2 slices out of 4 slices. So now if you add both, you will have 3 slices out of 4 slices which can be represented as $\dfrac{3}{4}$.

$\dfrac{1}{4}+\dfrac{2}{4}=\dfrac{(1+2)}{4}=\dfrac{3}{4}$

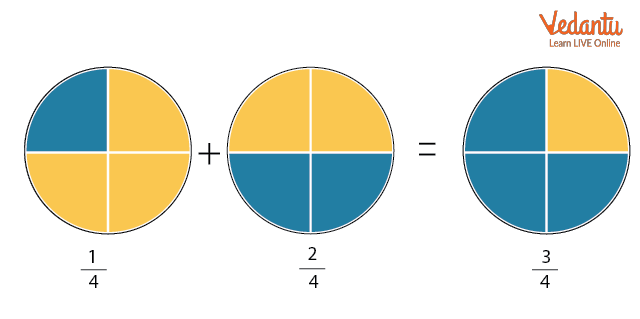
So from above, we can conclude that if the denominator is the same for both fractions then we can simply add the numerators.

If the denominators are different then we have to take the LCM of the denominators to make the denominator same for all fractions.

Let’s say, we want to add $\dfrac{1}{4}$ and $\dfrac{1}{2}$. Here denominators are different; so we will take LCM of 2 and 4 which will be 4.

$\dfrac{1}{4}+\dfrac{1}{2}=\dfrac{1}{4}+\dfrac{1 \times 2}{2 \times 2}$

$\dfrac{1}{4}+\dfrac{1}{2}=\dfrac{1}{4}+\dfrac{2}{4}$

$\dfrac{1}{4}+\dfrac{1}{2}=\dfrac{3}{4}$

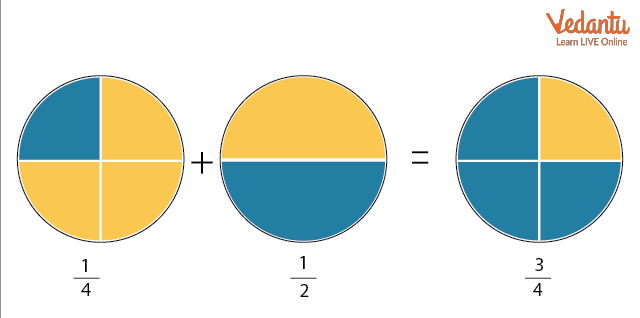
Subtraction of Fractions

Let’s understand the subtraction of fractions with the help of an example.

If your sister got 2 slices and you got 1 slice of a pizza out of 4 slices then find how many more slices your sister got out of 4. So you can see that your sister got one more slice than you out of 4.

We can represent it as:

$\dfrac{2}{4}-\dfrac{1}{4}=\dfrac{(2-1)}{4}$

$\dfrac{2}{4}-\dfrac{1}{4}=\dfrac{1}{4}$

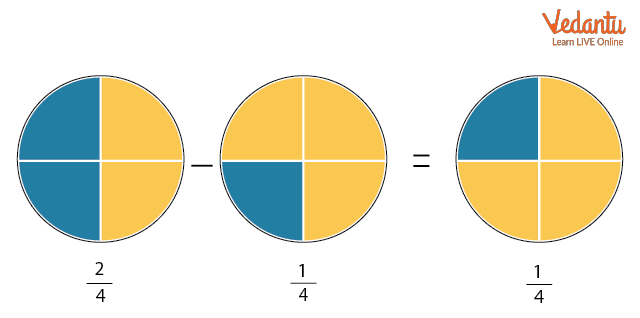
If the denominators are different then we have to take the LCM of denominators to make the same denominator for all fractions.

Let us subtract $\dfrac{1}{4}$ from $\dfrac{1}{2}$. Here the denominators are different so we will take the LCM of 2 and 4 using the division method.

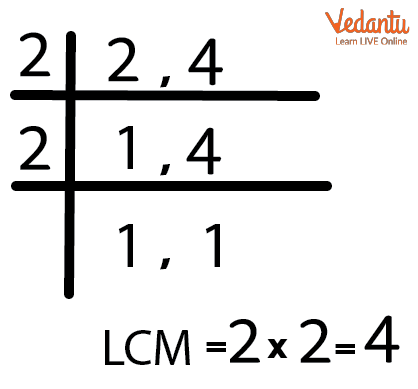
So, LCM is 4.

The denominator of one fraction is already 4 and the denominator of another fraction is 2. So, we will multiply numerator and denominator by 2 to equate both the denominators.

$\dfrac{1}{2}-\dfrac{1}{4}=\dfrac{1 \times 2}{2 \times 2}-\dfrac{1}{4}$

$\dfrac{1}{2}-\dfrac{1}{4}=\dfrac{2}{4}-\dfrac{1}{4}$

$\dfrac{1}{2}-\dfrac{1}{4}=\dfrac{1}{4}$

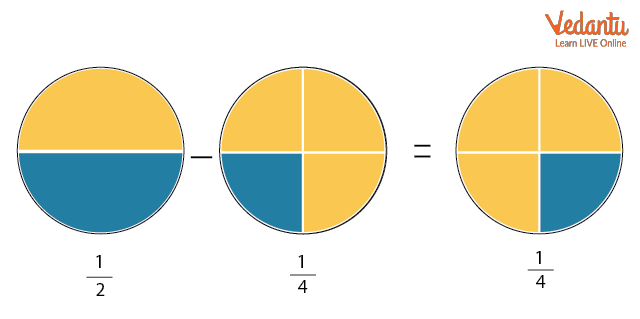
Multiplication of Fractions

Multiplication of fractions is one of the easiest operations of fractions. If we are multiplying two fractions, then we can simply multiply the numerator with the numerator and the denominator with the denominator. For example,

$\dfrac{1}{2} \times \dfrac{4}{5} = \dfrac{1 \times 4}{2 \times 5}$

$\dfrac{1}{2} \times \dfrac{4}{5} = \dfrac{4}{10}$

We can simplify the fraction to the simplest form if needed.

$\dfrac{1}{2} \times \dfrac{4}{5} = \dfrac{2}{5}$

To write in the simplest form, we have to divide both numerator and denominator by the same number. For example, $\dfrac{4}{10}$, if we divide 4 and 10 by 2 then we get the fraction as $\dfrac{2}{5}$. It is not possible to simplify further so this is the simplest form of a fraction.

We can understand this with the pizza example only. Let's suppose  that five friends went for a picnic. All of them had 1 pizza each.

At lunchtime, 4 out of 5 friends ate half of their pizza. How many parts of the total 5 pizzas have they eaten?

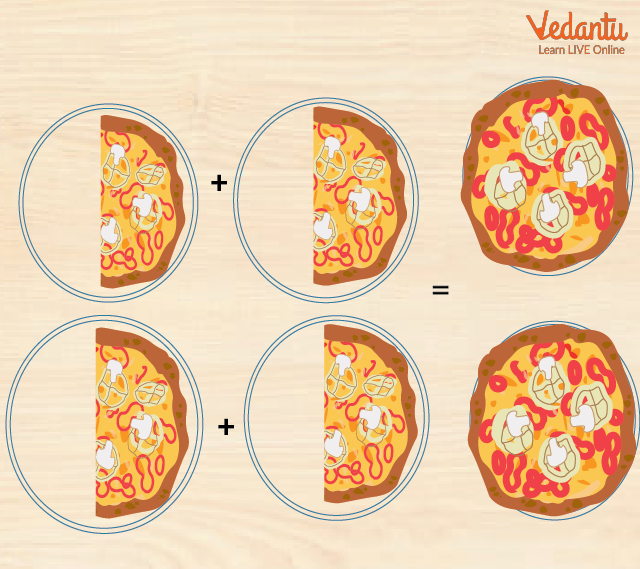
So, since 4 friends ate half of their pizza, in total, they have eaten 2 complete pizzas. Thus, you can say that out of 5 ,they have eaten 2 pizzas.

Division of Fractions

Division of fractions is almost similar to the multiplication of fractions but in division, we have to convert division into multiplication first. To convert division into multiplication, we have to interchange the numerator and denominator of the second fraction (Divisor). For example,

$\dfrac{1}{2} \div \dfrac{5}{4} = \dfrac{1}{2} \times \dfrac{4}{5}$

$\dfrac{1}{2} \div \dfrac{5}{4} = \dfrac{1 \times 4}{2 \times 5}$

$\dfrac{1}{2} \div \dfrac{5}{4} = \dfrac{4}{10}$

Fun Facts

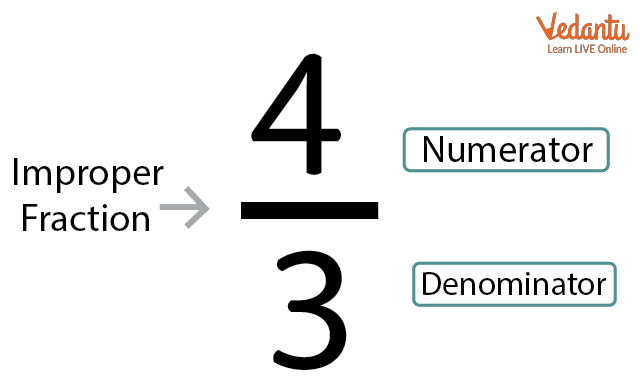
• In a fraction, the numerator can be greater than the denominator. In this case, the fraction is known as an improper fraction.

Solved Examples

1. There is a watermelon that is sliced into 10 equal parts. Sachin gets 4 slices and Pramod gets 3 slices. Find the fractions of their combined slices to total slices.

Ans: We have a watermelon which is sliced into 10 parts, so here the denominator in the fraction will be 10.

Now for Sachin, the number of slices is 4 and for Pramod, the number of slices is 3.

To find out the fraction of their combined slices to the whole slices, we must add both the fractions.

As the denominator for both the fractions is the same, we simply add the numerator to find out the new numerator.

4+3=7

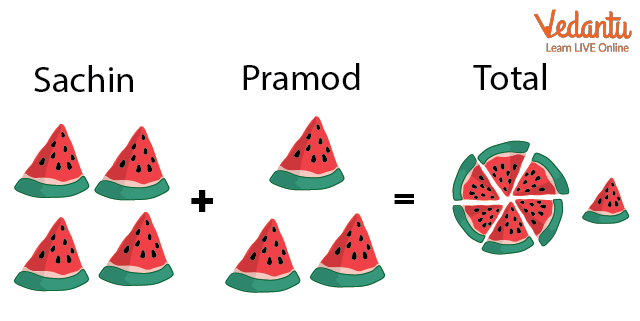
So, the fraction of slices they were given out of total slices is $\dfrac{7}{10}$.

2. There is a watermelon that is sliced into 12 equal parts. Robins gets 5 slices and Vijay gets 3 slices. Find the fractions of slices that will be given to Arun if the watermelon is completely distributed among them.

Ans: We have a watermelon which is sliced into 12 parts, so here the denominator in the fraction will be 12.

Now for Robins, the number of slices he gets is 5 and for Vijay, the number of slices is 

3.

Now to find out the number of slices that were given to Arun, we will subtract slices of both Robins and Vijay from 12.

Arun = 12 - (Vijay + Robin )

Arun = 12 - (3 + 5)

Arun = 12 - 8

Arun = 4

As the denominator for all the fractions is the same, we will simply add the numerator to find out the new numerator.

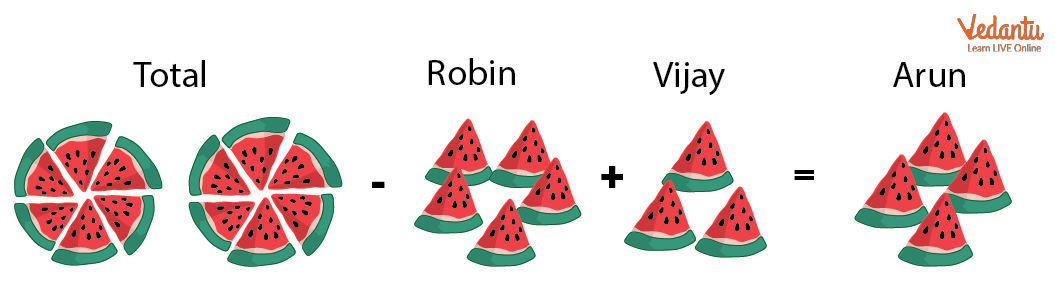
So, the total fraction of slices given to Arun is $\dfrac{4}{12}$.

3. Find the product of two fractions $\dfrac{3}{5}$ and $\dfrac{1}{2}$.

Ans: We have to multiply both the fractions then multiply the numerator with the numerator and the denominator with the denominator.

$\dfrac{3}{5} \times \dfrac{1}{2}=\dfrac{3 \times 1}{5 \times 2}$

$\dfrac{3}{5} \times \dfrac{1}{2}=\dfrac{3}{10}$

Summary

In this article, we have discussed the operations of fractions. First, we have discussed fraction definition, its representation, and operations of fractions. Then we listed down a fun fact and finally solved the problems.

Learning By Doing

Turn your name into the below fractions:

1. The fraction of the capital case letters.

2. The fraction of the small case letters.

3. The fraction of the vowel letters.

4. The fraction of the consonant letters.