Measuring Area and Describing Paths on a Grid

A math grid is another name for the coordinate plane consisting of a space of small squares, sometimes with an x-axis and y-axis. Each little square is used as a measurement. Every square could measure one unit area or more depending on what is needed and what you decide. Each column or row of squares could also have a unique verbal title, like in the case of bar graphs (where each column has a different name). In this article, we will learn how to measure the area, describe it by using paths on a grid, and count them over a grid.

How to Measure Area?

Measuring area and describing paths on a grid is done using a square-sized box row. These boxes are equal in length and breadth. These can be used for drawing models of things, working out geometry and trigonometry problems, and for making calculations.

Now let us see through an example:

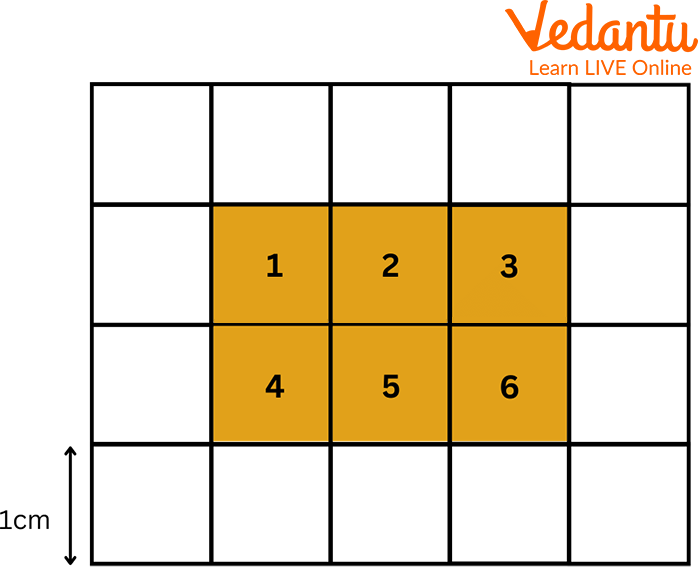
Here in the below image, we can see that the boxes are like graph paper having each of the boxes with equal sides. Let us suppose each box is of 1 unit.

Therefore, there are 35 boxes.

Here, by combining the length, it can be seen that it is 7 units.

And the width is 5 units.

So, we can say that the area of the whole box becomes:

= 7 x 5

= 35 unit²

We can also find the area of the shaded portion. As each box is of 1 unit².

Since there are 9 shaded boxes.

Hence, the area becomes 9 unit²

The Area of the Rectangle is the Number of Shaded Unit Squares

Area of Rectangle

Consider a yellow rectangle in the grid with an area of 6 units.

Example

In the above figure, the length of the rectangle is 3 units, and the width is 2 units. The area of a rectangle can be obtained by multiplying its length and width, which is the same as counting the unit squares.

Area of Rectangle = length × width

Therefore, the required area is = 2 x 3

= 6 square units

Area of Square

The coloured square shown below in the grid occupies 25 squares

Therefore, the area of the square will be multiplied by its sides.

Area of Rectangle

Area Of Square = side × side.

So, the required area is = 5 x 5 = 25 square units

Paths on a Grid

Given Below is an 8 by 8 grid. Let Point A be at the top left corner of the square and point B be in the bottom right corner.

If you are supposed to have only one more down and right and make a unique path in a grid, how many different paths will exist from A to B?

Paths on Grid

Every successful path for an 8x8 grid will involve exactly 7 moves down and 7 moves to the right. The number of decisions to select the right or the down path will determine the total number of paths. This way, we can count all possible paths from top left to bottom right.

Counting Paths

How does one realise the many pathways on a square when three lines go across every way, from point A to point B (from top to bottom)?

The problem, as declared, could be very little unclear as to wherever A and B are and what the rules are.

Making an Orderly List

Let's number the points to make it easier to discuss:

Starting at A=1, you have two choices, 2 or 4, so the possible paths so far are:

1-2

1-4

From 2, there are two choices, 3 or 5; from 4, there are two choices, 5 or 7:

1-2-3

1-2-5

1-4-5

1-4-7

From 3 or 7, there are no more choices; you're forced to go one way. From 5, you have two choices. So here are all the possible paths:

1 - 2 - 3 - 6 - 9

1 - 2 - 5 - 6 - 9

1 - 2 - 5 - 8 - 9

1 - 4 - 5 - 6 - 9

1 - 4 - 5 - 8 - 9

1 - 4 - 7 - 8 - 9

So we have a total of 6 paths (in red, from green A to red B):

Counting Paths

Solved Examples

Example 1: Find the area of a square with a side of 5 cm.

Solution: Area of a square = side × side.

Here, side = 5 cm

Substituting the values, 5 × 5= 25

Therefore, the area of the square = 25 sq cm.

Example 2: The dimensions of a rectangle are 15 cm and 8 cm. Find its area.

Solution: The area of a rectangle is the product of its length and width, which can be

Given, length = 15cm

Width = 8

Represented by the formula: Area = l × w.

Substituting the given values,

We get area of the rectangle = 15 × 8 = 120 square cm

Practice Questions

Q.1 Maggie's ping pong table is 9 feet long and 5 feet wide. What is the area of the rectangular playing surface of the ping pong table?

1. 28 square feet

2. 36 square feet

3. 45 square feet

4. 54 square feet

Ans. c. 45 square feet

Q 2 The area of a rectangle with a base of 4 inches and a width of 5 inches is

1. 20 square inches.

2. 9 square inches.

3. 18 square inches.

4. 10 square inches.

Ans. a.20 square inches

Summary

In this article, we have learnt about the area and how to find the area of various shapes and figures like squares and rectangles. Then we find their unique path in a grid, easily counting all possible paths from top left to bottom right. We have also solved some problems with them. This article also has a practice module that makes you practice the questions and helps you command the topic easily.