




How to Apply the Intercept Theorem in Maths Problems
The Intercept Theorem is a fundamental tool of Euclidean Geometry. The concept of parallel lines and transversal is of great importance in our day-to-day life. And, the Intercept theorem extends our understanding of parallel lines and transversal and we can apply these concepts in our day-to-day life.

A Transversal
In the above figure, we can see that there are 3 parallel lines ${L}_{1}$,${L}_{2}$, ${L}_{3}$ and then there is a transversal $PR$ which is intersecting all the 3 parallel lines at an equal distance. The intercept theorem, also known as Thale’s theorem, Basic Proportionality Theorem, or side splitter theorem, is an important theorem in elementary geometry about the ratios of various line segments that are created if two intersecting lines are intercepted by a pair of parallels.
History of the Mathematician

Euclid
Year of Birth: 325 BC
Year of Death: 270 BC
Contribution: He contributed significantly in the field of Mathematics and Physics by discovering the intercept theorem.
Statement of the Theorem
If there are three or more parallel lines and the intercepts made by them on one transversal are equal, the corresponding intercepts of any transversal are also equal.
Proof of the Theorem

Two Parallel Lines
Given:
$l$, $m$, $n$ are three parallel lines.
$P$ is a transversal intersecting the parallel lines such that $AB=BC$.
The transversal $Q$ has the intercepts $DE$ and $HE$ by the parallel lines $l$, $m$, $n$.
To prove:
$DE=EF$
Proof:
Draw a line $E$ parallel to the line $P$ which intersects the line $n$ at $H$ and line $l$ at $G$.
$AG||BE$ (Given)
$GE||AB$ (By construction)
From the information above, we can say that $AGBE$ is a parallelogram.
According to the properties of a parallelogram:
$AB=GE$ - (1)
Similarly, we can say that $BEHC$ is a parallelogram.
$BC=HE$ - (2)
From the given information, we know that $AB=BC$.
So, from equations (1) and (2), we can say that $GE=HE$.
In $\Delta GED$ and $\Delta HEF$,
$GE=HE$(Proved)
$\angle GED=\angle FEH$(Vertically Opposite Angles)
$\angle DGE=\angle FHE$(Alternate Interior Angles)
Hence, $\Delta GED\cong \Delta HEF$
As$\Delta GED\cong \Delta HEF$, the sides$DE=EF$.
Hence proved.
Applications of the Theorem
The intercept theorem can be used to prove that a certain construction yields parallel line segments:
If the midpoints of two triangle sides are connected, then the resulting line segment is parallel to the third triangle side (Mid point theorem of triangles).
If the midpoints of the two non-parallel sides of a trapezoid are connected, then the resulting line segment is parallel to the other two sides of the trapezoid.
Limitations of the Theorem
The intercept theorem is not able to help us in finding the midpoint of the sides of the triangle.
The basic proportionality theorem is an advanced version of the intercept theorem and it gives us a lot of information on the sides of the triangles.
Solved Examples
1. In a \[\Delta ABC\], sides \[AB\] and \[AC\] are intersected by a line at \[D\] and \[E\], respectively, which is parallel to side \[BC\]. Prove that \[\dfrac{AD}{AB}=\dfrac{AE}{AC}\].
Ans:

Scalene Triangle
\[DE||BC\] (Given)
So, \[\dfrac{AD}{DB}=\dfrac{AE}{EC}\]
Interchanging the ratios,
\[\dfrac{DB}{AD}=\dfrac{EC}{AE}\]
Adding 1 to both sides,
\[\dfrac{DB}{AD}+1=\dfrac{EC}{AE}+1\]
\[\dfrac{AD+DB}{AD}=\dfrac{EC+AE}{AE}\]
\[\dfrac{AB}{AD}=\dfrac{AC}{AE}\]
Interchanging the ratios again,
\[\dfrac{AD}{AB}=\dfrac{AE}{AC}\]
Hence proved.
2. Find DE
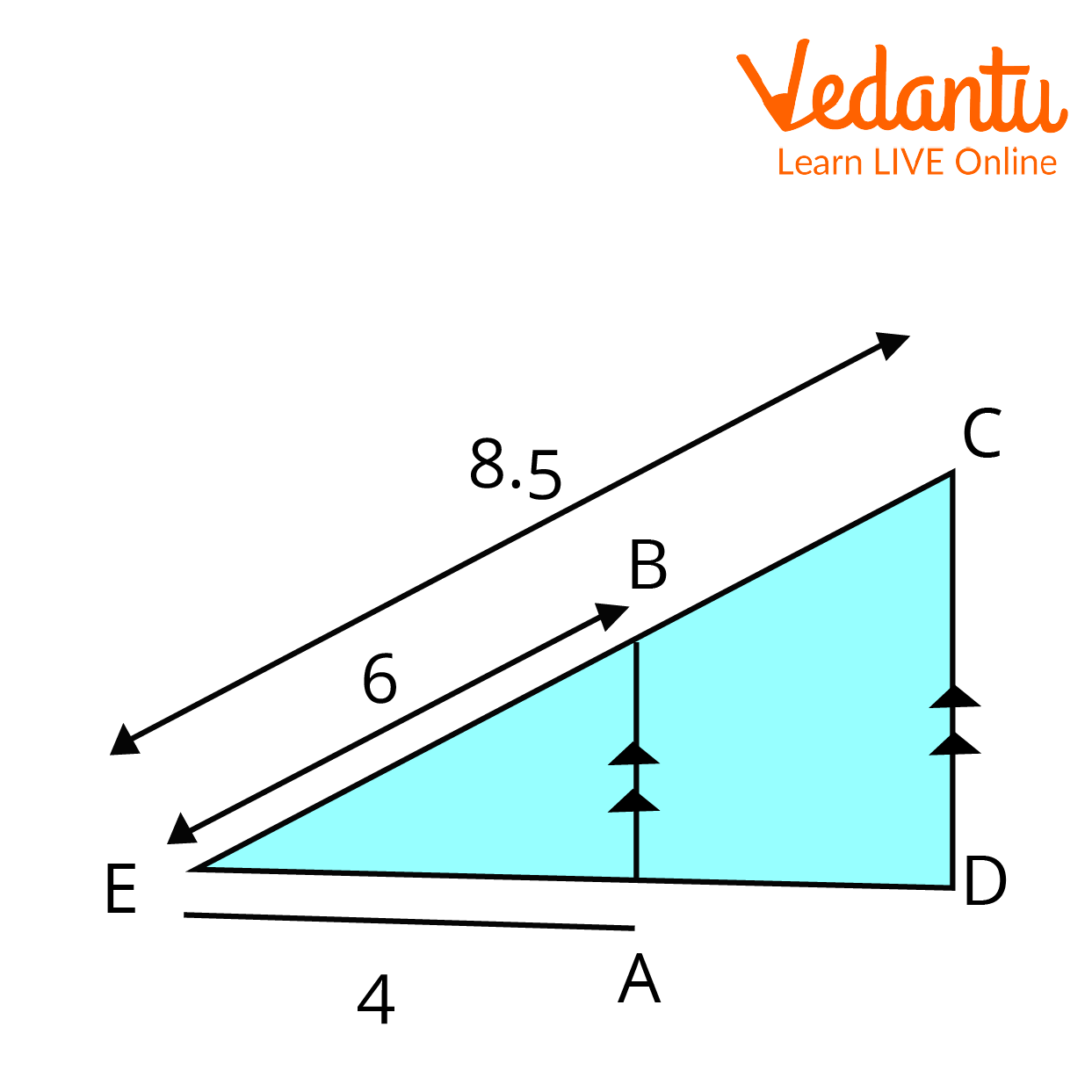
Basic Proportionality Theorem
Ans: According to the basic proportionality theorem,
\[\dfrac{AE}{DE}=\dfrac{BE}{CE}\]
\[\dfrac{4}{DE}=\dfrac{6}{8.5}\]
\[\dfrac{4*8.5}{6}=DE\]
\[DE=5.66\]
So, \[DE=5.66\]
3. In \[\Delta ABC\], \[D\] and \[E\] are points on the sides \[AB\] and \[AC\], respectively, such that \[DE||BC\]. If \[\dfrac{AD}{DB}=\dfrac{3}{4}\] and \[AC=15cm\], find \[AE\].

Intercept Theorem
Ans:\[\dfrac{AD}{DB}=\dfrac{AE}{EC}\] (According to the intercept theorem)
Let \[AE=x\] and \[EC=15-x\]
\[\dfrac{AD}{DB}=\dfrac{3}{4}\] (Given)
So, \[\dfrac{3}{4}=\dfrac{x}{15-x}\]
\[3(15-x)=4x\]
\[45=7x\]
\[x=\dfrac{45}{7}\]
\[x=6.4cm\]
So, \[x=6.4cm\]
Important Points
The intercept theorem can only be applied when the lies are parallel, if the transversal is cutting lines that are not parallel, then the intercept theorem is not valid.
The basic proportionality theorem and mid-point theorem are all applications of the intercept theorem but they are not the same theorems.
Conclusion
In the above article, we have discussed the Equal intercept Theorem and its proof. We have also discussed the applications of the theorem. So, we can conclude that Intercept Theorem is a fundamental tool of Geometry and is based on applications of parallel lines and transversal and reduces our computational work based on its application as we have seen in the examples based on the theorem.
FAQs on Intercept Theorem Explained for Students
1. What is the intercept theorem in mathematics?
The intercept theorem states that when two or more parallel lines intersect two transversals, the respective segments on one transversal are proportional to the corresponding segments on the other. It is also known as Thales' theorem in geometry.
2. How is the intercept theorem used in geometry?
In geometry, the intercept theorem is used to solve problems involving parallel lines and proportional segments. It helps to determine unknown segment lengths by setting up a proportion based on the parallel lines crossing two transversals.
3. What is the formula for the intercept theorem?
The intercept theorem formula is written as $\frac{AB}{BC} = \frac{DE}{EF}$, where AB and BC are segments on one transversal and DE, EF are the intercepted segments on another transversal, when intersected by several parallel lines.
4. Can you provide an example of the intercept theorem?
Suppose three parallel lines cross two transversals, creating segments of 4 cm and 8 cm on the first, and 6 cm and x cm on the second. By the intercept theorem: $\frac{4}{8}=\frac{6}{x}$. Solving gives $x=12$ cm.
5. Why is the intercept theorem important in mathematics?
The intercept theorem is important because it provides a quick method for finding lengths in geometric figures involving parallel lines. It teaches
- proportional reasoning
- spatial understanding
- simplifies complex diagrams
6. What is the difference between the intercept theorem and Thales' theorem?
Thales' theorem typically refers to the result that any angle inscribed in a semicircle is a right angle. However, in many regions, the term also describes the intercept theorem, which relates to segment proportionality. Check the context or textbook being used.
7. What are some real-life applications of the intercept theorem?
The intercept theorem is used in fields like
- architecture
- engineering
- map making
8. How do you prove the intercept theorem?
To prove the intercept theorem, draw two transversals intersected by parallel lines. Use similar triangles formed by connecting intersection points. Since corresponding sides are proportional in similar triangles, segment ratios created by parallel lines must also be equal.
9. What are the conditions for using the intercept theorem?
The intercept theorem requires:
- at least two parallel lines
- two transversals that intersect the parallels
- corresponding segments on each transversal
10. Can the intercept theorem be applied in triangles?
Yes, if a line is drawn parallel to one side of a triangle intersecting the other two sides, the intercept theorem states that the segments formed are proportional. This is useful for dividing triangles in geometric constructions and proofs.
11. What is a practical tip for solving intercept theorem problems?
When using the intercept theorem, always label all intersection points clearly and write down the ratios before substituting values. Setting up the correct proportion equation makes it easier to solve for unknown segment lengths accurately.





































