




How to Convert Improper Fractions to Mixed Numbers Efficiently
Improper fractions are fractions having a numerator greater than the denominator. Here, fractions are representing something in parts. For example, you have 5 pieces of cake and after eating three pieces, you are left with two pieces. Now, how do you represent the remaining part? Well, it is simple, you write it as ⅖. Here, ⅖ is the fraction of the cake left with you.
In another case, you add 1 more piece of cake, then at present, you have\[ \frac{2}{5} \] + 1 = \[ \frac{7}{5} \] pieces of cake. So, here you notice that the numerator ‘7’ is greater than the denominator ‘5’, which means that this fraction is improper. We can also write \[ 1\tfrac{2}{5} \] piece of cake. This is how we understand what an improper fraction is.
In real life, mixed fractions can be easily understood when compared to improper fractions. However, we can easily convert any improper fraction to a mixed number or vice-versa by following some basic steps that you will study in later sections on this page with solved examples.
Concept of Improper Fractions
From the above text, we understand that improper fractions have numerators greater than or equal to its denominator. For example, \[ \frac{11}{5} \], \[ \frac{13}{4} \] are improper fractions.
Numerically, we find that these fractions are always equal to or greater than 1. We can write a mixed fraction from improper fractions. So, such a type of fraction carries a combination of a natural number and a proper fraction. The simplified form of an improper fraction becomes a mixed fraction, for example,\[ 25\frac{4}{3} \] and \[ 25\tfrac{4}{3} \] are mixed fractions. Numerically, we notice that a mixed fraction is always greater than 1. Also, we can rewrite a mixed fraction in the form of an improper fraction.
Steps to Convert Improper Fractions to Mixed Numbers
Please note that the denominator of the mixed fraction form is always the same as that of the original fraction, i.e., of an improper fraction. Mixed numbers are the simplified form of improper fractions, that’s why it becomes important to learn this conversion. For converting an improper fraction to a mixed number, we need to follow the below-listed steps:
Step 1- Divide the numerator with the denominator, for example, if the fraction is \[ \frac{21}{4} \], then divide \[ \frac{21}{4} \]
Step 2- Now, when you divide the numerator, you get a quotient and a remainder. Here, you get the quotient as 5 and the remainder as 1.
Step 3- Now, we arrange the values of the quotient, remainder, and divisor, i.e., 5, 1, and 4 in the following manner to express a fraction as a mixed fraction:
Quotient = \[ \frac{Remainder}{Divisor} \]
Here, for the above values, you get \[ 5\tfrac{1}{4} \] as a mixed fraction corresponding to the improper fraction of \[ \frac{21}{4} \]
Like you can see under the division method for an improper fraction \[ \frac{13}{4} \]:

Converting Improper Fraction to a Mixed Fraction
How To Solve Improper Fractions?
Solving an improper fraction is like solving any proper fraction, the only difference that comes here is, we have to simplify the answer and form mixed numbers.
Let's solve the improper fraction: 9/5 + 8/5.
Step 1: We notice that we have the same denominator for both the fractions. Therefore, we will directly add the numerators 9 and 8. We get 17. Thus, on adding improper fractions, we get \[ \frac{17}{5} \]
Step 2: Simplifying the improper fraction (i.e., dividing 17 by 5), we will get 3 as a whole (which is a quotient), 2 as a numerator (remainder), and 5 as the denominator (divisor).
Using the formula Quotient = \[ \frac{Remainder}{Divisor} \]
we get: \[ 3\frac{2}{5} \], which is a mixed fraction corresponding to \[ \frac{17}{5} \]
Convert Improper Fraction to Decimal
Example 1: Convert 10/4 improper fraction to a decimal.
The first step we need to do is, divide 10 by 4. We know that 10 ÷ 4 = 2.5. Now, let us follow the long-division method here:
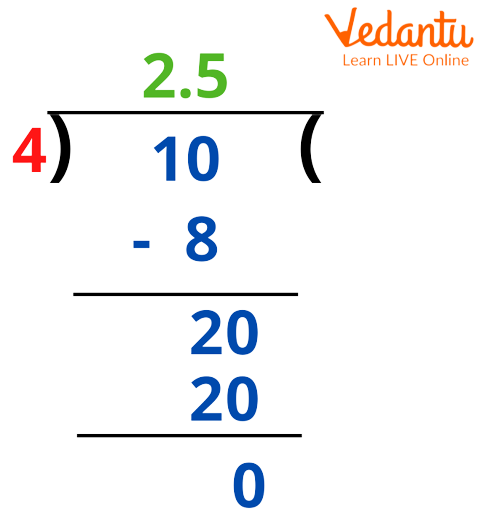
Converting Improper Fraction to Decimal
Here, 10/4 is an improper fraction and 2.5 is a decimal. We can write 2.5 as 5/2, which is an improper fraction. Also, \[ 2\tfrac{1}{2} \] makes it a mixed fraction because 2 is a whole number and \[ \frac{1}{2} \] is a proper fraction.
From the above text, we understand that solving improper fractions is similar to performing arithmetic operations on numbers simplifying the value of the answer so obtained. There are four arithmetric operators which are addition, subtraction, multiplication, and division.
FAQs on Improper Fractions Made Easy: Definitions, Steps & Examples
1. What is an improper fraction, and can you provide some examples?
An improper fraction is a type of fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). This means the fraction represents a value of 1 or more than 1. For example, if you have 5 slices of a pizza that was cut into 4 equal parts, you have 5/4 of a pizza.
Examples of improper fractions include:
- 5/4 (numerator 5 > denominator 4)
- 11/6 (numerator 11 > denominator 6)
- 7/7 (numerator 7 = denominator 7, which equals 1 whole)
- 12/5 (numerator 12 > denominator 5)
2. What is the main difference between a proper fraction, an improper fraction, and a mixed fraction?
The main difference lies in the relationship between the numerator and the denominator, which determines the fraction's value.
- A proper fraction has a numerator that is smaller than its denominator, like 3/4 or 2/5. Its value is always less than 1.
- An improper fraction has a numerator that is greater than or equal to its denominator, like 7/4 or 5/5. Its value is always 1 or greater than 1.
- A mixed fraction combines a whole number and a proper fraction, like 1 ¾. It is just another way to write an improper fraction. For example, 1 ¾ is the same as 7/4.
3. How can you convert a mixed fraction into an improper fraction?
To convert a mixed fraction, such as 3 ⅖, into an improper fraction, you can follow these simple steps:
- Step 1: Multiply the whole number by the denominator of the fraction. (In this case, 3 × 5 = 15).
- Step 2: Add the result to the numerator of the fraction. (15 + 2 = 17).
- Step 3: This new number becomes the numerator of the improper fraction. The denominator stays the same.
So, the mixed fraction 3 ⅖ is equal to the improper fraction 17/5.
4. Why is the value of an improper fraction always greater than or equal to one?
The value of an improper fraction is always 1 or more because of what a fraction represents. The denominator tells you how many equal parts one whole object is divided into. The numerator tells you how many of those parts you have. In an improper fraction like 8/5, the whole is divided into 5 parts, but you have 8 parts. Since you have more parts than what makes up a single whole, the total value must be more than one whole. If the numerator and denominator are equal, like 5/5, you have all the parts that make up one whole, so its value is exactly 1.
5. How do you add or subtract improper fractions?
To add or subtract improper fractions, they must first have a common denominator. If they already do, you simply add or subtract the numerators and keep the denominator the same. For example, 7/5 + 4/5 = 11/5.
If the denominators are different, like in 5/3 + 7/4, follow these steps:
- Find the Least Common Multiple (LCM) of the denominators. The LCM of 3 and 4 is 12.
- Convert each fraction to an equivalent fraction with the new denominator (12). For 5/3, multiply the numerator and denominator by 4 to get 20/12. For 7/4, multiply by 3 to get 21/12.
- Now, add or subtract the new numerators: 20/12 + 21/12 = 41/12.
6. How can you visualise an improper fraction like 7/3?
Visualising an improper fraction helps in understanding its value. To visualise 7/3, you can think of objects divided into thirds, like circles or rectangles.
- First, understand that the denominator '3' means each whole object is split into 3 equal parts.
- The numerator '7' means you need to shade 7 of these parts.
- You would take one whole circle, divide it into 3 parts, and shade all 3. You have now used 3 parts.
- You take a second whole circle, divide it into 3 parts, and shade all 3. You have now used a total of 6 parts (3+3).
- You still need one more part, so you take a third whole circle, divide it into 3 parts, and shade just one.
You end up with two completely shaded circles and one-third of a third circle. This visually shows that 7/3 is the same as 2 ⅓.
7. In what situations are improper fractions more useful than mixed numbers?
While mixed numbers are often easier to understand in everyday contexts (e.g., "2 ½ cups of flour"), improper fractions are generally more useful and less prone to errors in mathematical calculations, especially for multiplication and division. When you multiply or divide fractions, using an improper fraction like 5/2 is much more direct than using its mixed form 2 ½. Converting mixed numbers to improper fractions first simplifies the calculation process and avoids common mistakes, making them essential for more complex algebraic operations.























