Importance of Angles
An angle measure can be defined as the measurement of an angle formed by the two rays or arms at a common vertex. We take the importance of angles for granted. Whenever two lines meet at a point, it forms an angle. The point where these lines meet is called a node or a vertex. The term "Angle" originated from the Latin "Angulus". If you look around, everything touching another surface is at some angle or the other.
Let's discuss the different types of angles, what they are called and how they are used in mathematics.
Types of Angles
Angles are named according to their measurements. Some of the angles which are important to understand include:
Acute angle
Acute Angle: An angle which is less than 90 degrees is acute.
Right Angle: An angle of exactly 90 degrees is a right angle.
Obtuse Angle: An angle greater than 90 degrees and less than 180 degrees is an obtuse angle.
Straight Angle: An angle which has a 180-degree angle is straight.
Different Types of Angles
Measurement of an Angle
To measure angle is typically thought to be the process of determining a specific angle, converting it into an equivalent angular measure and calculating its lower or upper tangent. The first question that comes to mind is, what is the definition of an angle?
The simple definition of an angle is the figure formed when two rays share a common endpoint.
The standard unit for measuring an angle is called a degree. The angles can be measured using a protractor.
We measure the angles with either a protractor or it can also be constructed using a compass.
An angle is measured in degrees, and so it is called degree measure—the measure of an angle formed by the two rays or arms at a common vertex.
Angle measurement is the amount of rotation from the initial to an endpoint of a ray.
The angle is said to be positive if the rotation is clockwise and negative if the rotation is anticlockwise.
Various units can measure Angles. The standard unit of measuring an angle is Degree and Radian.
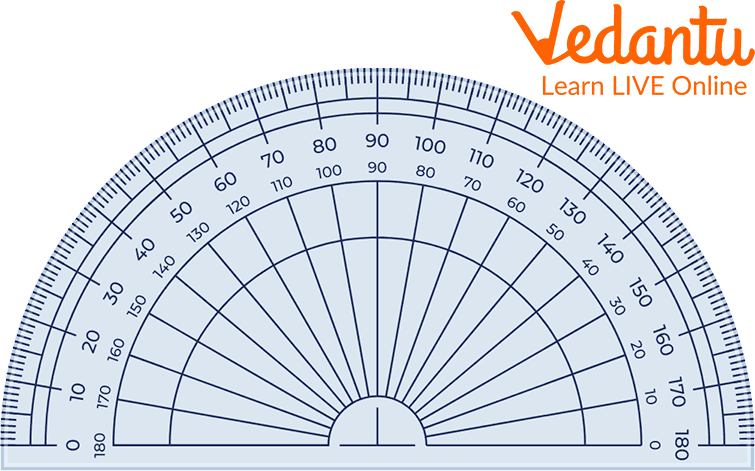
Protractor
Use of Angles in Everyday Life
Here are a bunch of ways you can use angles to get the most out of your life!
Visualise: Angles can help you understand complex problems. For instance, with a problem that needs more than one angle to solve, you can draw the shapes and think about the angles easily.
Use Angles in Life: You can also use them in life. For example, driving is one of those activities where there are a lot of traffic signs. So drawing down an angle helps you remember what sign to look for in conversation.
Carpenters use them to measure precisely to build doors, chairs, tables, etc.
Athletes use them to gauge the distances of a throw and enhance their sports performance.
Engineers construct buildings, bridges, houses, monuments, etc., using angle measurement.
Solved Examples
Q 1. What is the measure of the angle in degrees between:
(i) North and West?
(ii) North and South?
(iii) North and South-East?
Direction
Ans: The measure of the angle between:
(i) North and west is $90^{\circ}$.
(ii) North and South is $180^{\circ}$.
(iii) North and South-East is $135^{\circ}$.
Q 2. How many angles are formed in the figures? Name them.
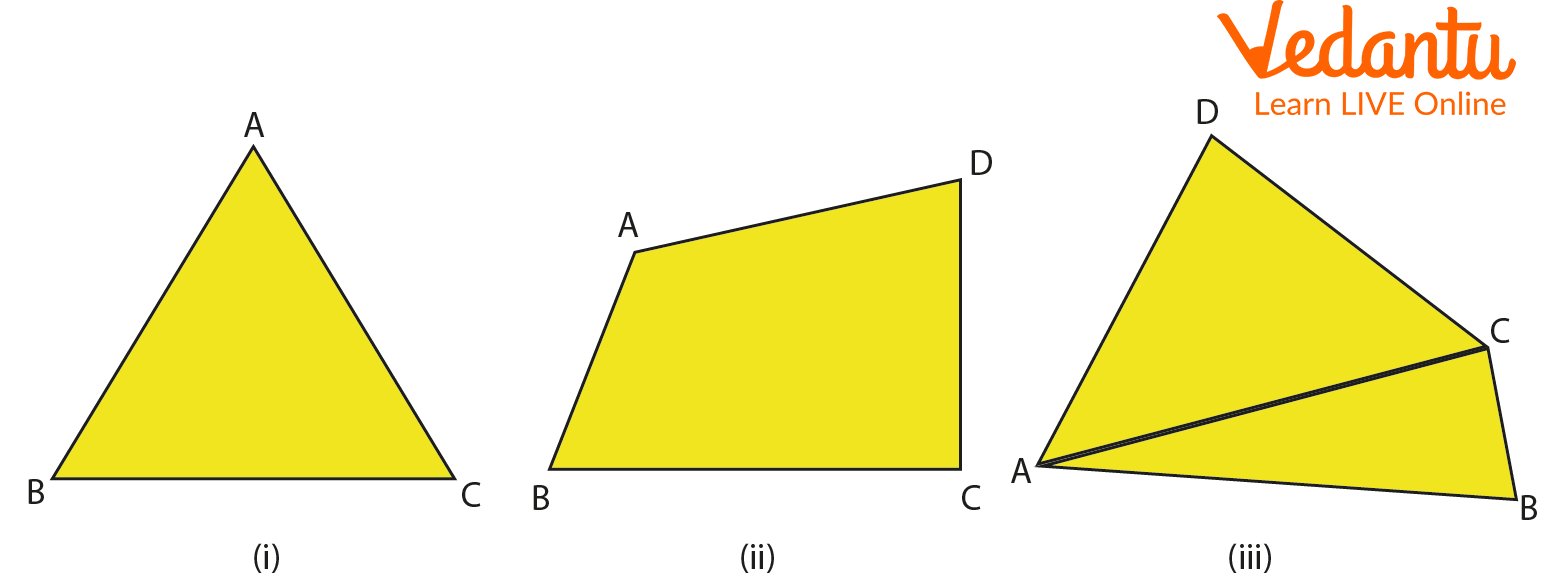
Angles
Ans: The angles formed in figure 1: $\angle{ABC}$,$\angle{ACB}$ and $\angle{BAC}$
The angles formed in figure 2: $\angle{ABC}$, $\angle{BCD}$, $\angle{CDA}$, $\angle{DAB}$.
The angles formed in figure 3: $\angle{ABC}$, $\angle{BCD}$, $\angle{CDA}$, $\angle{DAB}$, $\angle{CAB}$, $\angle{CAD}$.
Q 3. Write two examples of obtuse angles and reflex angles.
Ans: As we know, obtuse angles are the angles that measure less than $180^{\circ}$ and greater than $90^{\circ}$
Examples: $112^{\circ}, 177^{\circ}$
Reflex angles measure less than $360^{\circ}$ and greater than $180^{\circ}$.
Examples: $210^{\circ}, 300^{\circ}$
Practice Questions
Q 1. Classify the following angles into acute, obtuse, right and reflex angles:
(i) 35°
(ii) 185°
(iii) 92°
(iv) 260°
Ans: (i) 35°: Acute angle
(ii) 185°: Obtuse angle
(iii) 92°: Obtuse angle
(iv) 260°: Reflex angle
Q 2. Classify the given angle in the image.
Angle
Ans: The given angle is making an angle of 90 degrees. So it is a right angle.
Q 3. How many 45-degree angles are there in a straight angle?
Ans: A straight angle divided into two halves will be 90° each, and 90° divided into two halves will be 45° each. So, there are four 45° angles in the straight line drawn. Therefore, four 45° angles make a straight line.
Summary
This includes all about types of angles, classification of angles, and measurement of angles. We have studied it with very simple definitions. Two rays intersecting at the same point is an angle. In all geometry shapes, angles are present. Angles are expressed in degrees. An angle can be measured by using a Protractor. An angle is an arc that joins two points on a straight line.
