




How to Apply the Hypotenuse Leg Theorem in Geometry
The longest side of a right-angled triangle, known as the hypotenuse, is always opposite to the right angle. According to the hypotenuse leg theorem, two right triangles are congruent if the hypotenuse and one leg of one right triangle coincide with the hypotenuse and leg side of the second right triangle. We employ the HL (Hypotenuse Leg) Theorem or the RHS (Right angle-Hypotenuse-Side) congruence rule to demonstrate the congruence of any two right triangles. In this article, we'll study more about the hypotenuse leg theorem.
Table of Contents
Introduction to Hypotenuse Leg Theorem
What is the Hypotenuse Leg Theorem?
Hypotenuse Leg Theorem Proof
Hypotenuse Leg Theorem Formula
Hypotenuse Leg Theorem Examples
What is the Hypotenuse Leg Theorem?
The hypotenuse leg theorem states that if one right triangle's hypotenuse and one of its legs are congruent with the other right triangle's hypotenuse and one of its legs, the two triangles are congruent. In other words, a collection of right triangles is said to be congruent if the hypotenuse and one leg of each triangle have the same length.
Hypotenuse Leg Theorem Formula
Consider following two right-angled triangles,
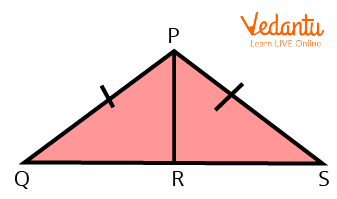
Right-Angled Triangles
By Hypotenuse Leg theorem,
If, \[\;PQ\; = \;PS\] (Hypotenuse)
\[PR\; = \;PR\] (Common side)
Therefore,
$\triangle PQR \cong \triangle PSR$
Hypotenuse Leg Theorem Proof
The hypotenuse leg theorem's proof demonstrates how a set of right triangles are congruent if the lengths of one of their associated hypotenuses and legs are the same. Look at the isosceles triangle ABC below, where the side \[AB\; = \; AC\] and AD is perpendicular to BC.
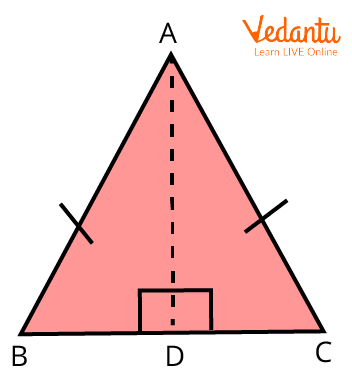
Hypotenuse Leg Theorem Proof
As an altitude, AD is perpendicular to BC and creates the right-angled triangles ADB and ADC. These triangles' respective hypotenuses, AB and AC, are equal.
Therefore, \[AB\; = \;AC\]
Due to their shared presence in both triangles, \[AD\; = \; AD\]
AD is common in both triangles.
Therefore, a hypotenuse and a pair of legs in two right triangles satisfy the hypotenuse leg theorem's definition.
Angles B and C are equal, as we know (Isosceles Triangle Property).
We are also aware of the equality of BAD and CAD angles. (BC is divided in half by AD, making BD equal to CD.)
Consequently,
Therefore, $\triangle ADB \cong \triangle ADC$.
Hence proved.
Applications of Hypotenuse Leg Theorem
The Hypotenuse leg theorem is a theorem that can be applied to demonstrate how two right triangles can be congruent.
The theorem can also be applied to prove the equality of any two right triangles' two sides.
Hypotenuse Leg Theorem Examples
1. Prove that $\triangle ABD \cong \triangle DBC.$ If $\angle A = \angle C = 90^{\circ},$ and \[AD\; = \;BC\].
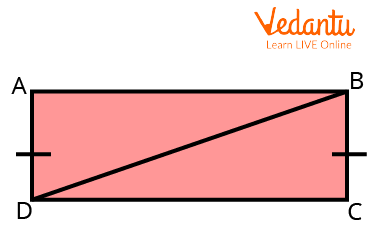
A Rectangle
Ans. We have,
\[AD\; = \;BC\] (equal leg)
\[\angle A = \angle C\] (right angle)
\[BD\; = \;DB\] (common side, hypotenuse)
By the Hypotenuse-Leg theorem,
$\triangle ABD\cong \triangle DBC$
Hence proved.
2. Let's assume that \[\angle W\; = \;\angle Z\; = \;90\;^\circ \], and M is the intersection of WZ and XY. Demonstrate the congruence of the two triangles, WMX and YMZ.

Combination of Triangles
Ans. Given that both $\triangle WMX$ and $\triangle YMZ$ have an angle of \[90^\circ \], they are right triangles (right angles)
\[WM\; = \;MZ\] (leg)
\[XM\; = \;MY\;\](Hypotenuse)
Consequently, according to the Hypotenuse-Leg theorem, $\triangle WMX$ and $\triangle YMZ$ are congruent.
3. Find the value of \[x\] and \[y\] for the given triangles, assuming that $\triangle ABC$ and $\triangle PQR$ are congruent to each other?
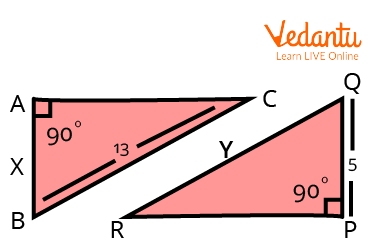
Two Triangles
Ans. By the Hypotenuse-Leg theorem,
In $\triangle ABC$ and $\triangle PQR$,
\[BC\; = \;QR\] (congruent hypotenuse)
Consequently, \[y\; = \;13\;,\;AB\; = \;PQ\] (congruent legs)
Thus, \[x\; = \;5\].
Thus, \[x\; = \;5\] and \[y\; = \;13\].
Conclusion
This article covered the Hypotenuse-Leg theorem and its proof in considerable detail. As a result of the discussion above regarding the Hypotenuse-Leg theorem, it is clear that if the sides and hypotenuse of any two triangles are equal, then the triangles must be congruent. The congruence of triangles and missing sides can be determined using this theorem.
The hypotenuse and one leg are the components that are used to test the congruence of triangles following the Hypotenuse-Leg Congruence rule.
The SAS (Side-Angle-Side) postulate and the Hypotenuse-Leg Congruence rule are related. The main distinction is that the Hypotenuse-Leg theorem uses the right angle, which is not the included angle between the hypotenuse and the leg, as the known angle. In contrast, SAS needs two sides and an added angle.
Related Links:
FAQs on Hypotenuse Leg Theorem Explained
1. What is the Hypotenuse-Leg (HL) Theorem in geometry?
The Hypotenuse-Leg (HL) Theorem is a criterion used to prove that two right-angled triangles are congruent. The theorem states that if the hypotenuse and one corresponding leg of two right-angled triangles are equal in length, then the two triangles are congruent.
2. What are the three essential conditions for applying the Hypotenuse-Leg (HL) Theorem?
To apply the HL Theorem, three specific conditions must be met:
- Two Right-Angled Triangles: The theorem is exclusively for triangles that each contain a 90° angle.
- Congruent Hypotenuses: The hypotenuses (the sides opposite the right angles) of both triangles must be equal in length.
- One Pair of Congruent Legs: At least one pair of corresponding legs (the sides adjacent to the right angle) must be equal in length.
3. Why does the Hypotenuse-Leg Theorem only work for right-angled triangles?
The HL Theorem's validity is fundamentally tied to right-angled triangles because the concept of a 'hypotenuse' only exists in a right-angled triangle. It is specifically the side opposite the 90° angle. Furthermore, the proof of the HL theorem relies on the Pythagorean theorem (a² + b² = c²), which itself only applies to right-angled triangles to establish the equality of the third side.
4. How is the Hypotenuse-Leg (HL) Theorem different from the SAS (Side-Angle-Side) congruence rule?
The key difference lies in the position of the angle. For the SAS (Side-Angle-Side) rule, the known angle must be the 'included' angle, meaning it is located between the two known sides. In the HL Theorem, the known angle is the 90° right angle, which is not between the hypotenuse and the leg. Therefore, HL is a special case of congruence that applies only to the unique geometry of right-angled triangles.
5. What are the main congruence criteria for triangles as per the CBSE syllabus?
According to the CBSE curriculum for Maths, there are five primary criteria for proving triangle congruence:
- SSS (Side-Side-Side): All three corresponding sides are equal.
- SAS (Side-Angle-Side): Two corresponding sides and the included angle are equal.
- ASA (Angle-Side-Angle): Two corresponding angles and the included side are equal.
- AAS (Angle-Angle-Side): Two corresponding angles and a non-included side are equal.
- RHS (Right-angle-Hypotenuse-Side): In two right-angled triangles, the hypotenuse and one corresponding side are equal. This is also known as the HL Theorem.
6. Can you provide a simple example of the Hypotenuse-Leg Theorem?
Certainly. Imagine two right-angled triangles, ΔABC (right-angled at B) and ΔPQR (right-angled at Q). If you are given that the hypotenuse of ΔABC (side AC) is equal to the hypotenuse of ΔPQR (side PR), and one leg of ΔABC (e.g., side AB) is equal to the corresponding leg of ΔPQR (side PQ), then you can conclude that ΔABC is congruent to ΔPQR by the HL Theorem.
7. How is the Hypotenuse-Leg (HL) Theorem proven?
The HL Theorem can be proven using the Pythagorean theorem and the SSS congruence criterion. If we have two right triangles, ΔABC and ΔDEF, with hypotenuses AC = DF and legs AB = DE. By the Pythagorean theorem, we know BC² = AC² - AB² and EF² = DF² - DE². Since AC = DF and AB = DE, it follows that BC² = EF², meaning BC = EF. Now, since all three corresponding sides are equal (AB=DE, BC=EF, AC=DF), the triangles are proven to be congruent by SSS (Side-Side-Side).
8. How do the HA (Hypotenuse-Angle) and LA (Leg-Angle) theorems relate to the HL theorem?
HA and LA are other congruence criteria specific to right-angled triangles, but they differ from HL:
- HL (Hypotenuse-Leg): Requires a congruent hypotenuse and a congruent leg.
- HA (Hypotenuse-Angle): Requires a congruent hypotenuse and a pair of congruent acute angles. This is essentially a case of the AAS criterion.
- LA (Leg-Angle): Requires a congruent leg and a pair of congruent acute angles. This can be a case of either ASA or AAS, depending on whether the leg is between the angles or not.
HL is unique because it's a Side-Side-Angle (SSA) case that works only for right triangles, whereas HA and LA are direct applications of the standard AAS/ASA rules.























