




Multiplying Fractions Made Easy: Rules, Tricks, and Common Mistakes
A fraction is a number that is a component of a whole. By breaking a whole into a number of parts, it is evaluated. If a fraction is expressed as a/b, then a and b are its components, with a serving as the fraction's numerator and b serving as its denominator. For example, if 1/2 is a fractional value then 1 is the numerator and 2 is the denominator and this value represents half of a whole number.

Introduction on how to Multiply Fraction
The product of a fraction by another fraction or an integer or a set of variables is referred to as the multiplication of a fraction.
Multiplication is actually a process of repetition of addition. Look at the image below to understand this. After reading this article one will be able to answer and solve questions like finding the product of fractions, how to multiply unlike fractions, etc.
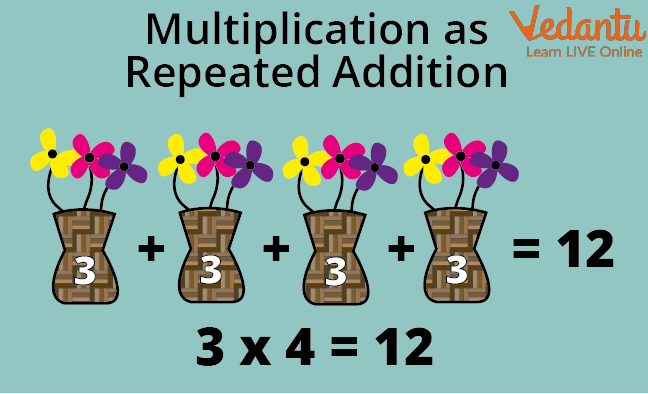
Multiplication as Repeated Addition
How to Multiply Fraction
The steps for multiplication of fractions are as follows:
Multiply the numerator with the numerator
Multiply the denominator with the denominator
Simplify the fractions(reduce the resultant fraction to its lowest term), if required.
Fractional Multiplication
Now, we'll talk about fractional multiplication by whole numbers, fractional numbers, and mixed fractional numbers.
Multiplication of Fraction by a Whole Number
To multiply a fraction with a whole number, first multiply the numerator of the fraction by the whole number and then reduce the fraction to the lowest terms, if required.
Let us multiply 2/3 by 4 to understand the multiplication of fractions by whole numbers. We use the rule of repeated addition to solve it.

Multiplication of Fraction by a Whole Number
That means, we can say that 2/3 of 4 is 8/3.
Multiplication of Fraction by another Fractional Number
When multiplying two or more fractions, the denominators are multiplied to obtain the product's denominator and the numerators are multiplied to obtain the new numerator of the product.
Let us multiply 1/4 by 1/2 to understand the multiplication of fractions by other fractional numbers.
To do so, first multiply the numerators, 1 by 1, and then multiply the denominators, 4 by 2.
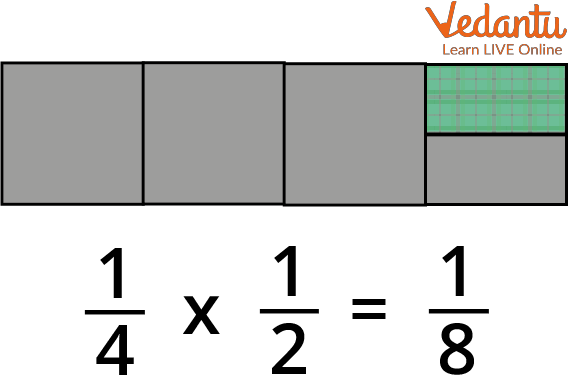
Multiplication of Fraction by another Fractional Number
That means, we can say that 1/4 of 1/2 is 1/8.
Multiplication of Fraction by a Mixed Number
To multiply a fractional number by a mixed number first convert the mixed number into an improper fractional number and then simply apply the rule we discussed above to multiply a fraction with another fractional number. Look at the example given below to understand this concept.
Let’s multiply 6 by 3$\frac{1}{4}$,
To find the product of the fraction and the mixed number, we will first simplify the mixed number 3 ¼ as;
(4 × 3 + 1)/4 = 13/4
Then,
6 × 13/4 = 78/4.
Multiplication of Fractions Examples
Let’s understand the concept better with some more multiplication of fractions examples.
Example 1: Multiply 4 by 2/8.
Ans: Multiply the numerator by 4.
4 × 2 = 8
That means, 4 × 2/8 = 8/8
Now reduce the resultant fraction to its lowest term,
8/8 = 1
Therefore, 4 by 2/8 = 1.
Example 2: Multiply 2/3 by 5/9.
Ans:
Step1. Multiply the numerators,
2 × 5 = 10
Step 2. Multiply the denominators,
3× 9 = 27
Therefore, 2/3 by 5/9 = 10/27.
Example 3: Multiply 2 1/3 by 5 2/5.
Ans:
Step1. Convert the mixed numbers to improper fractions,
(2 × 3+1)/3 × (5 ×5+2)/5 = 7/3 × 27/5
Multiply and simplify;
7/3 × 27/5 = 189/15.
Therefore, 2 1/3 by 5 2/5 = 189/15.
Practice on your own
Q1. Multiply 2/7 by 3.
(Ans. 6/7)
Q2. Multiply 1 1/2 by 4 4/7.
(Ans. 96/14)
Q3. Multiply 5 by 8/10.
(Ans. 4)
Summary
Multiplication of fractions refers to the operation of multiplying one fraction by another fraction, an integer, or a collection of variables. We can easily find the product of fractions by following a simple three-step procedure, first, multiply the numerators then the denominators and finally reduce the product to its lowest term if required.
FAQs on How to Multiply Fractions: Simple Steps and Examples
1. How to multiply unlike fractions and explain it with the help of an example?
Just as we multiply two fractions i.e a fractional number with another fractional number, we can also multiply unlike fractions (the fractional numbers with different numerators or denominators or both). This can be better understood by the following example.
Consider if we have to multiply 2/5 by 1/2,
To do so, first, we will multiply the numerators i.e. multiply 2 by 1, and then the denominators i.e. multiply 5 by 2.
Hence, the product of the 2/5 by 1/2 is 1/5.
2. What is the difference between proper fractions and improper fractions?
A portion of a whole is described by a fraction. The denominator, which is represented by the number at the bottom of the fraction, indicates the number of equally-sized pieces into which the whole is divided. The numerator, which is the number at the top of the fraction, indicates how many parts we are taking. The fraction 5/4, for instance, means "5 of 4 equal portions." The numerator is 5, and the denominator is 4.
A fraction with a smaller numerator than the denominator is said to be a correct fraction. A fraction whose numerator is the same as or bigger than its denominator is said to be inappropriate. Proper fractions include 1/4, 3/7, and 9/17, while improper fractions include 15/2, 28/15, and 25/11.























