




How to Solve HCF Problems: Step-by-Step Guide for Students
Highest Common Factor (HCF) as the name itself says, it's the method of finding the highest common factors of two or more than two numbers. It's the highest common number which can divide the given two or more than two positive numbers equally.
To find the HCF, we first need to find out the factors of each given number. Then we check for the common factors where the factors that we found out are the same and lastly we mark the highest factor of them all.
For example:
Let's take two positive numbers
1. Find out the HCF of 6,12.
Ans:
Step 1- Finding out the factors
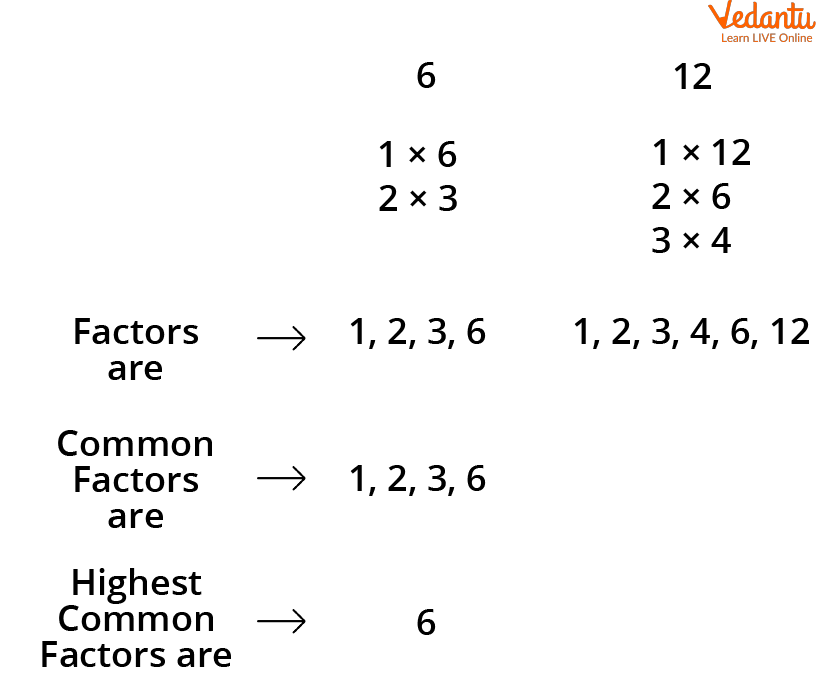
Factors of 6,12
Step 2: finding out the common factors
The factors of 6 and 12 are 1, 2, 3, 6
The Highest Common Factor of (6,12) = 6
Understanding How to Find HCF Using Short Division Method
1. Find out the HCF of 36 and 45.
Ans: The easiest method of finding out the HCF of large numbers is using the short division method.
For this method, we need to find out the LCM (least Common Multiple) of 36 and 45. Firstly draw a table and arrange the given numbers horizontally. We need to find out the common factors which can divide the given number equally and put it on the left hand side.

LCM Method to Find Out Common Factors
We keep on dividing until we get co-prime numbers at the end. Prime number is a number that cannot be exactly divided by any other whole number other than itself and 1.
In this case. we got 4 and 5 which don't have common factors. Lastly, we multiply all the common factors that we have.
3X3 = 9
Therefore, the HCF of (36, 45) = 9.
HCF Word Problem
1. A milk seller has 120 liters of almond milk and 180 liters of soya milk. He wants to sell the milk by filling both the kinds of milk in tins of equal amount. Find the greatest volume of which the tin can take.
Ans: To find out the equal quantity of both the milks that the tin can take, we need to find out the factors of 120 and 180;
Well the target of the question is to find out the greatest volume of milks filled in the tins. So, we have to find the largest number which exactly divides 120 and 180 equally which means we will have to find out the HCF of 120 and 180.
Using LCM to find out the common factors

LCM of 120, 180
HCF of (120, 180)=> 2X2X15 = 60
Therefore, the greatest volume that the tins can take is 60 liters of each.
Which means 120 ÷ 60 = 2 tins of almond milk
180 ÷ 60 = 3 tins of soya milk.
Practice Questions
1. Sneha has 40 strawberries and Eisha has 95 blueberries. They want to distribute the fruits in such a way that each box has an equal number of fruits and also each box should have the exact set of strawberries or blueberries. What is the greatest number of fruits that can be arranged in each box?
Ans: HCF of (40,95)= 5
Therefore, the fruits in the boxes can be arranged equally in the set of 5.
2. Two wooden boards are 77 m and 44 m long respectively. The wooden boards are to be cut into pieces of equal length. Find the maximum length of each board.
Ans: HCF (77,43)= 11
Therefore, the wooden boards can be cut into 11 equal lengths.
Summary
In this article we learnt that HCF (highest common factor) also known as GCD (greatest common divisor) basically is the number which can divide the given two or more numbers equally and one of the easiest ways of finding out the HCF of large numbers is using the Short division method. The article tries to explain the short division method step-by-step properly.
FAQs on HCF Questions and Practice Problems
1. What is the Highest Common Factor (HCF) and why is it important in Maths?
The Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), is the largest positive integer that divides two or more numbers without leaving a remainder. For instance, the HCF of 12 and 18 is 6. It's a fundamental concept in number theory, important for simplifying fractions to their lowest terms and for solving various problems related to division and distribution.
2. What are the common methods used to find the HCF of numbers as per the CBSE syllabus?
According to the CBSE curriculum for the 2025-26 session, there are two primary methods for finding the HCF:
- Prime Factorisation Method: This involves breaking down each number into its prime factors. The HCF is the product of the lowest powers of all common prime factors.
- Long Division Method: In this method, the larger number is divided by the smaller number. The divisor is then divided by the remainder, and this process continues until the remainder is zero. The last divisor is the HCF.
3. How can we find the HCF of 24 and 36 using the prime factorisation method?
To find the HCF of 24 and 36, we first list their prime factors:
- Prime factors of 24 = 2 × 2 × 2 × 3 = 2³ × 3¹
- Prime factors of 36 = 2 × 2 × 3 × 3 = 2² × 3²
The HCF is the product of these values: HCF (24, 36) = 2² × 3¹ = 4 × 3 = 12.
4. How is HCF applied to solve real-world problems?
HCF is used in practical scenarios that require splitting different quantities into identical, smaller groups without any leftovers. For example, it can be used to:
- Find the largest possible size for square tiles that can pave a rectangular floor without any cutting.
- Determine the maximum number of students per row if students from different classes are to be arranged in rows with an equal number in each.
- Distribute different items (e.g., pens, pencils, erasers) into the maximum number of identical kits.
5. What is the key difference between HCF and LCM?
The key difference lies in their purpose. The HCF (Highest Common Factor) is the largest number that can divide a set of numbers, used for splitting or grouping. In contrast, the LCM (Lowest Common Multiple) is the smallest number that is a multiple of all numbers in a set, often used to find when recurring events will happen simultaneously.
6. Can the HCF of a set of numbers be 1? What are such numbers called?
Yes, the HCF of two or more numbers can be 1. This occurs when the numbers have no common factors other than 1. Numbers with an HCF of 1 are known as co-prime numbers or relatively prime numbers. For instance, the numbers 9 and 10 are co-prime because their HCF is 1.
7. What is a common mistake students make when finding the HCF of three numbers?
A common mistake is finding a factor that is common to only two of the three numbers and including it in the HCF calculation. For the HCF, a prime factor must be present in the prime factorisation of all the numbers involved. For example, when finding the HCF of 12, 18, and 30, the common prime factors are 2 and 3. The HCF is 2 × 3 = 6.
8. Why is the HCF of any two distinct prime numbers always 1?
By definition, a prime number has only two factors: 1 and itself. When you take two different prime numbers (e.g., 5 and 11), their factors are {1, 5} and {1, 11}. The only factor they share is 1. Therefore, their Highest Common Factor must be 1, making them co-prime by default.

















