




How to Find the Highest Common Factor of 30: Explained
What if you need to find the maximum common dimension for any two clothes having different sizes?. Here we use HCF as the most common and most efficient way.
The HCF of two numbers is the biggest number that can divide both evenly.
HCF can be evaluated for two or more numbers.
The greatest common factor of any two numbers will divide it completely or equally the given numbers.
For example – the HCF of 9 and 15 is 3. Because 3 is the largest number it can divide 9 and 15 exactly.
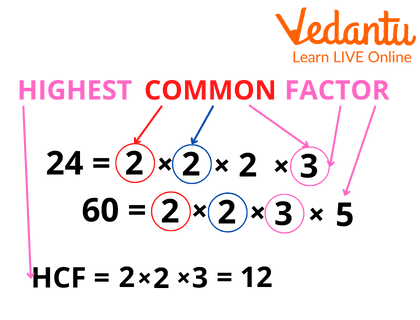
HCF
Methods To HCF
There are two methods of finding HCF.
Division method
Prime Factorization Method
Prime factorization is the simple process of finding the prime numbers when multiplied together to get the original number.
To understand it better let’s solve one example , Are you Ready!
Let’s start
Find the common factors of 30 and 45.
Find HCF of 30 and 45,
First, we will get each number as a product of prime factors.
So, for 30 = 2 x 3 x 5
And for 45 = 3 x 3 x 5
The product of all common prime factors is the HCF
2 x 3 x 5
3 x 3 x 5
The blue colour is common in both.
So the HCF = 5 X 3 = 15.
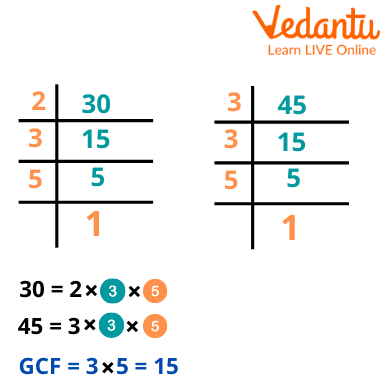
HCF of 30 and 45
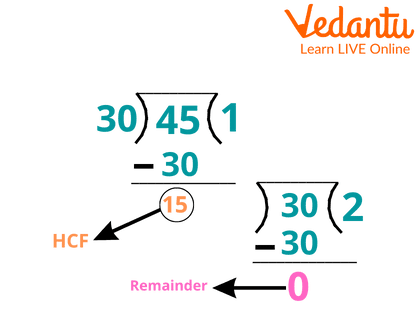
Division Method
In the division method, we will divide the largest number by the smallest number until we get the remainder as 0.
To understand it better, let's solve an example.
We will use same question, we have used for prime factorization method
Let’s Start
Find HCF of 30 and 45,
HCF of 30 and 45
As we can see in the image, the greatest number 45 is divided by the smallest number 30. After diving, we get a remainder of 15. Now we have 15 and 30, we will repeat the method. We will divide the largest number by the smallest here. The largest number is 30 and the smallest number is 15. We will divide 30 by 15 and we get the remainder as 0. Hence, the HCF of 30 and 45 is 15.
HCF Solved Examples
Question 1: find HCF of 30 and 50
Solution: 30 = 2 x 3 x 5
50= 2 x 5 x 5
HCF = 2 x 5 =10.
Question 2: Find the HCF of 30 and 60 by both methods.
Solution:
HCF of 30 and 60 by factorization method
30 = 2 x 3 x 5
60 = 2 x 2 x 3 x 5
So here 2,3 and 5 are the common factors in it.
HCF = 2 x 3 x 5 = 30
HCF = 30
HCF of 30 and 60 by division method
Ans:

HCF of 30 and 60
As after dividing the largest number by smallest we are getting 0 as remainder.
So the HCF will be 30
HCF = 30.
HCF Properties
Let’s see some interesting properties of HCF –
The HCF of two numbers cannot be greater than any of them.
If one number is the factor of another number, the smaller number will be the HCF in this case.
Eg:- HCF of 10 and 5 will be 5 only.
The HCF of two numbers is the product of common prime factors.
The HCF of co-prime numbers will always be equal to 1. (same goes for prime numbers also.
HCF Math Question
Question 1: What is the greatest number which can divide 44, 70, and 82?
Solution: By prime factorization method;
44 = 2 x 2 x 11
70 = 2 x 5 x 7
82 = 2 x 41
So here 2 is the only common factor for 44, 70 and 82
HCF = 2.
Question 2: Find the HCF of 20 , 50
Solution: In the fraction, we have to do the HCF of all the numerators and LCM of all the denominators.
So we have to find HCF of 20,50
And LCM of 20 , 50
Let’s find HCF first,
20= 2 x 2 x 5
50 = 2 x 5 x 5
2 and 5 the only common factor here,
So HCF = 2 x 5 = 10
Summary
In this article, we got to know about HCF. It can be found for 2 or more numbers. We also learnt that there are 2 methods to find HCF. We can find HCF either by prime factorization or by division method. We got to know about its properties and real-life use of it. And now we can use this knowledge to solve various types of HCF-related problems.
FAQs on HCF of 30: Easy Steps, Examples & Practice
1. What does the HCF of a number like 30 actually represent?
The HCF (Highest Common Factor) of a set of numbers is the largest positive integer that divides each of the numbers without leaving a remainder. When we talk about the HCF involving 30, we are looking for the biggest number that can divide both 30 and any other given numbers in the set perfectly. For example, the HCF of 30 and 45 is 15, because 15 is the largest number that divides both 30 and 45.
2. How can we find the HCF of 30 using the prime factorisation method?
The prime factorisation method is an effective way to find the HCF. To find the HCF of 30 and another number (e.g., 42), you follow these steps:
- First, find the prime factors of each number. For 30, the prime factorisation is 2 × 3 × 5.
- Next, find the prime factors for the other number. For 42, it is 2 × 3 × 7.
- Identify the common prime factors in both lists. Here, the common factors are 2 and 3.
- Finally, multiply these common prime factors together to get the HCF. So, HCF = 2 × 3 = 6.
3. What are the common factors of 30 and 45, and which one is the HCF?
To find the HCF by listing common factors, you first list all factors for each number.
- The factors of 30 are: 1, 2, 3, 5, 6, 10, 15, and 30.
- The factors of 45 are: 1, 3, 5, 9, 15, and 45.
4. Are HCF (Highest Common Factor) and GCF (Greatest Common Factor) different concepts?
No, HCF and GCF are not different concepts. They both refer to the exact same mathematical idea: the largest number that divides a given set of integers. The term HCF is more commonly used in the Indian curriculum (like CBSE/NCERT), while GCF is more prevalent in other international curriculums, such as in the United States. They are completely interchangeable.
5. What is the real-world importance of finding the HCF?
The HCF is a very useful concept with several real-world applications. For instance, it helps to:
- Simplify fractions: To simplify a fraction to its lowest terms, you divide both the numerator and the denominator by their HCF.
- Organise items into groups: If you want to split different quantities of items into the largest possible equal groups with nothing left over, you would find the HCF. For example, arranging 30 chocolates and 45 biscuits into identical gift baskets.
- Solve design and measurement problems: HCF can be used to determine the largest size of square tiles that can pave a rectangular floor without any cutting.
6. Why is the HCF of 30 and a co-prime number like 17 always 1?
By definition, two numbers are co-prime if their only common factor is 1. The factors of 30 are {1, 2, 3, 5, 6, 10, 15, 30}, and the factors of 17 (which is a prime number) are just {1, 17}. When you compare these two sets of factors, the only number they have in common is 1. Therefore, the Highest Common Factor (HCF) must be 1. This is true for any pair of co-prime numbers.
7. Is it possible for the HCF of 30 and another number to be larger than 30?
No, it is not possible. The HCF of a set of numbers must be a factor of every number in that set. This means it must be able to divide each number without a remainder. A number larger than 30 (e.g., 31) cannot divide 30. Therefore, the HCF of a group of numbers can never be greater than the smallest number in the group. The HCF of 30 and 45, for instance, is 15, which is smaller than 30.
8. What is the quickest way to find the HCF of 30 and 90?
The quickest method, in this case, is by observation. If one number in the set is a factor of the other number, then the smaller number is the HCF. Here, 30 divides 90 exactly (90 ÷ 30 = 3). Therefore, 30 itself is the largest number that can divide both 30 and 90. So, the HCF of 30 and 90 is 30. This shortcut is much faster than using prime factorisation for such cases.

















