Fraction of Collection

Remember how it is served to you when you buy a pizza to eat? Though the pizza is circular, it is cut into several parts, for ex: 4, 6, 8, etc., before serving. These parts are nothing but fractional parts of the whole pizza.

A fraction is a part of a whole number. Therefore, the fraction tells you about the parts made of a whole object, number, etc. In India, fractions were first written with one number above another (numerator and denominator) but without a line. It was the Arabs only who added the line, which is used to separate the numerator and the denominator. We will understand more about this as we move along with the article.

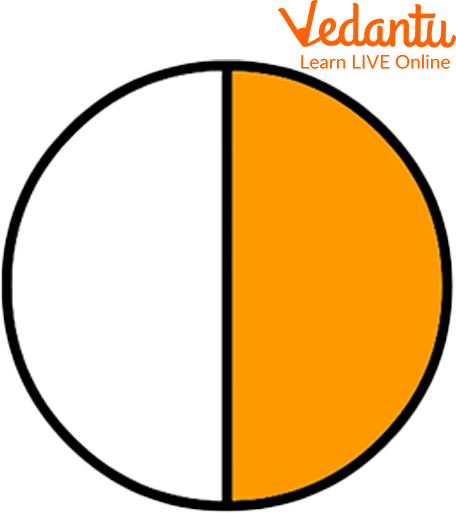
Fraction Images

Way to Represent Fractions

To write a fraction, you must write the number in the numerator and then use the division symbol. Then you have to write the number in the denominator. For example, if you want to write a fraction with numerator 37 and denominator 53, this is how you represent the fraction. i.e. $\dfrac{37}{53}$

Fractions of Collection of Numbers or Objects

Now you know about fractions of whole numbers or objects. Let us understand what fractions of the collection of numbers are.

A fraction can be a portion or section of any quantity out of a whole, where the whole can be any number, a specific value, or a thing. Let us understand this concept using an example. The following figure shows a pizza that is divided into 8 equal parts. Now, if we want to express one selected part of the pizza, we can express it as $\dfrac{1}{8}$, which shows that out of 8 equal parts, we are referring to 1 part.

It means one in eight equal parts. It can also be read as:

One-eighth, or 1 by 8

1 by 8 Pizza

Learning with Examples

Examples are always fun as they help you learn about a topic in a very practical way. You will better understand fractions of collections once you try out some examples and fraction images.

Example 1

There are 15 apples in the basket. You have to divide them into three groups. To divide 15 apples into 3 portions, each group would receive $\dfrac{1}{3}$rd of the total number of apples. Thus, we would have to divide 15 by 3 to get the one-third value. The one-third portion of 15 apples is 5 apples, and the fraction would be $\dfrac{3}{15}$. This is equal to $\dfrac{1}{5}$, in reduced form. Therefore, each group receives 5 apples.

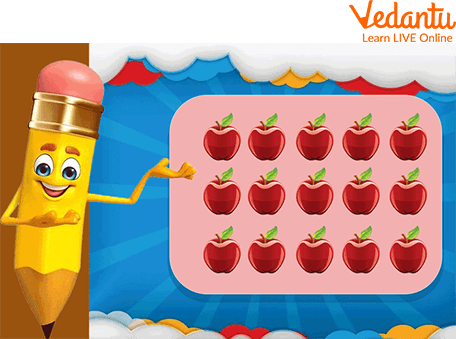
15 Apples Into 3 Shares

Example 2

There is a collection of 8 mugs, and you have to separate them into two halves. To calculate the half of 8, we have to divide 8 by 2. As half of 8 is 4, one-half of 8 mugs would be 4 mugs. Therefore, the fraction would be $\dfrac{4}{8}$, which is equal to $\dfrac{1}{2}$. The numerators in these fractions are 4 and 1, whereas the denominators are 8 and 2.

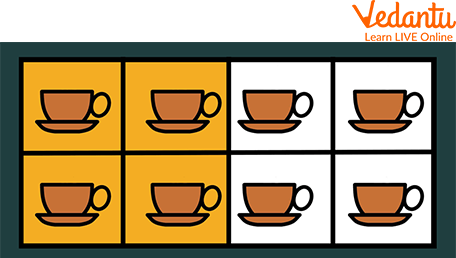
Two Shares of 8 Mugs

Practice Questions

Here is a fraction of the collection worksheet for you to practise. Solving these practice questions will help you better understand the concept.

1. Express the shaded regions in the figure as a fraction.

Fractions

Ans: $\dfrac{1}{4}$

2. If a cake is cut into 6 pieces, how would you write ‘four pieces out of six’ as a fraction?

Ans: $\dfrac{4}{6}$

3. In a cricket team of 11 players, if 6 players are batsmen, and the rest of the players are bowlers, how do you represent the number of bowlers in fractional form?

Ans: $\dfrac{5}{11}$

Summary

This article taught us about fractions, their representation, and the calculation of fractions in a collection of numbers. First, we learned about fractions with an example of pizza. Then we understood how to calculate fractions of the collection of numbers. We tried a few examples where we learned how fractions are made with multiple objects Then, at the end of the article, we added practice questions to get hands-on with the fraction.