Definition Properties Rules and Solved Examples of Division
One of the four fundamental arithmetic operations, or how numbers are combined to create new numbers, is division. The other operations are multiplication, addition, and subtraction. At a fundamental level, counting the instances in which one number is included within another is one interpretation of the division of two natural numbers.
Division facts are number phrases that relate to knowing the times tables.
What is Division Fact?
1. If the dividend is "zero," any number used as a divisor will result in a "zero" quotient.
2. Any dividend will have a quotient equal to itself if the divisor is "1".
3. The dividend is always equal to the product of the divisor and the quotient added to the remainder.
Dividend = (Divisor Quotient) + Remainder.
Division Facts for Multiplication
A fact involving multiplication is the result of two distinct integers. Additionally, the product is unaffected by the arrangement of the numbers. For instance, \[3 \times 2 = 6{\rm { \;and\; }} 2 \times 3 = 6\] .
These days, division facts are frequently taught with multiplication facts as fact families. For instance, a student learning the numbers 2, 3, and 6 would be aware that\[3 \times 2 = 6{\rm{ and }}2 \times 3 = 6\], and that \[\frac{6}{2} = 3{\rm { and }} \frac{6}{3} = 2\] . No matter how multiplication facts are taught, they can only be learnt via practice. Fortunately, there are a lot of tools available to assist your child master multiplication.
Division Facts for Zero
Any number used as a divisor will result in a "zero" quotient if the dividend is "zero." A fraction with zero as the denominator is created when a positive or negative number is divided by zero. To express zero divided by a negative or positive value, a fraction with zero as the numerator and the finite amount as the denominator is employed. Divided by it, zero equals zero.
Division Fact
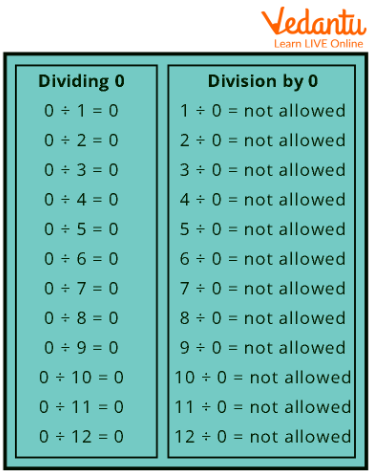
Division Facts for Zero (Tabular Form)
Division Facts Examples Image:
Division Facts
Solved Examples(Division Facts with Answers):
Example 1: What is \[32 \div 8?\]
Ans: We know that \[8 \times 4 = 32\]
Thus, \[32 \div 8 = 4\]
Answer is 4.
Example 2: What is \[40 \div 10\] ?
Ans: As we know \[10 \times 4 = 40\] ;
Therefore \[40 \div 10 = 4\]
Answer will be 4.
Example 3: If Shrilly had 49 chocolates and she wants to distribute them in her friends group. There are a total 7 members in the Shrilly group. Help her out in distributing the chocolate so that every member gets an equal number of chocolates.
Ans: Total Number of chocolates Shrilly had = 49
Number of friends = 7
For distributing them \[49 \div 7\] chocolates will be the precise way.
As we know, \[7 \times 7 = 49\].
Thus, \[49 \div 7 = 7\]
Therefore, each member will get 7 chocolates.
Conclusion
One of the four fundamental arithmetic operations is division, which is the process of combining two numbers to create a new number. The remaining operations are multiplication, addition, and subtraction.
FAQs on Understanding Division Facts and Key Concepts
1. What is division in Maths?
Division is the mathematical operation of splitting a number into equal parts or groups. It is the inverse of multiplication and is represented by the symbol ÷ or /.
- In division, the number being divided is called the dividend.
- The number you divide by is the divisor.
- The result is called the quotient.
2. What are the basic terms used in division?
The four main terms in division are dividend, divisor, quotient, and remainder. These terms describe each part of a division problem.
- Dividend: The number being divided (e.g., 15 in 15 ÷ 4).
- Divisor: The number you divide by (e.g., 4).
- Quotient: The answer (e.g., 3).
- Remainder: The amount left over (e.g., 3 in 15 ÷ 4 = 3 R3).
3. What is the formula for division?
The standard division formula is Dividend = Divisor × Quotient + Remainder. This is known as the division algorithm.
- Example: 17 ÷ 5 = 3 R2
- Check: 5 × 3 + 2 = 15 + 2 = 17
4. How do you solve a long division step by step?
Long division is solved by dividing, multiplying, subtracting, and bringing down digits in order. Follow these steps:
- Divide the first digit(s) of the dividend by the divisor.
- Multiply the divisor by the quotient digit.
- Subtract the result from the current number.
- Bring down the next digit and repeat.
5. What is the difference between division and multiplication?
Division splits a number into equal parts, while multiplication combines equal groups into a total. They are inverse operations.
- Multiplication example: 4 × 3 = 12
- Division example: 12 ÷ 3 = 4
6. What happens when you divide a number by zero?
Dividing any number by zero is undefined. There is no real number that can multiply by 0 to give a non-zero number.
- Example: 5 ÷ 0 has no value.
- However, 0 ÷ 5 = 0, because zero divided by any non-zero number equals zero.
7. What are the properties of division?
Division has specific properties, but it is not commutative or associative. Key properties include:
- Not commutative: 8 ÷ 4 ≠ 4 ÷ 8
- Not associative: (16 ÷ 4) ÷ 2 ≠ 16 ÷ (4 ÷ 2)
- Identity property: a ÷ 1 = a
- Zero property: 0 ÷ a = 0 (a ≠ 0)
8. How do you divide fractions?
To divide fractions, multiply the first fraction by the reciprocal of the second fraction. The rule is a/b ÷ c/d = a/b × d/c.
- Example: 3/4 ÷ 2/5
- Step 1: Flip 2/5 to 5/2
- Step 2: Multiply → (3/4) × (5/2) = 15/8
9. How do you divide decimals?
To divide decimals, make the divisor a whole number by moving the decimal point in both numbers equally. Then divide as usual.
- Example: 4.8 ÷ 0.6
- Move decimal one place right → 48 ÷ 6
- 48 ÷ 6 = 8
10. Can you give a real-life example of division?
Division is used in real life to share or distribute items equally. For example, if 20 candies are shared among 5 children, each child gets 4 candies.
- Total candies (dividend) = 20
- Number of children (divisor) = 5
- Candies per child (quotient) = 4
