




Practical Examples: Drawing Perfect Parallel Lines for Math Success
A set square or triangle is an object used in engineering and technical drawing, with the aim of providing a straightedge at a right angle or another particular planar angle to a baseline.
The simplest form of a set square is a triangular piece of transparent plastic (or formerly of polished wood) with the center removed. More commonly the set square bears the markings of a ruler and a half-circle protractor.
Using a fixed square to draw parallel lines is an accurate method. A rectangular drawing tool called a "set square" is used to draw vertical lines, parallel lines, and some common angles. Lines that never cross each other are said to be parallel.
Parallel Lines
Two lines in the same plane that are equally spaced apart and never cross each other are said to be parallel lines in geometry. Both horizontal and vertical shapes are possible. Examples of parallel lines can be found everywhere, including zebra crossings, rows of notebooks, and the nearby railroad tracks.

Parallel Lines
What is Set Square
A set square is used in technical drawings and math practice to represent predefined angles. Setting rectangles are typically made of thin plastic, wood, or, in rare cases, thin steel and have a triangular shape. Every plane represents three different angles, always containing one right angle. There are two common combinations of given set square angles: the \[{30^{^o}} - {60^o} - {90^o}\] option and the \[{45^o} - {45^o} - {90^o}\] option.

Set Square
Correct Use of Set Square
To use set squares correctly:
One side of the desired angle set must be set on a solid, level bottom line, such as the cross-arm of a T-square that is typically perpendicular to the paper and is oriented at a known angle.
The other edge of the established angle is then often marked off using a pencil or pen.
Use of Set Square
Following is the list of the uses of set square:
Draw a vertical line
Draw vertical corners
Draw a standard measurement angle [the two given rectangles are named after their angles; one is 90, 30, and 60 degrees, and the other is 90 and 45 degrees.
Parallel lines can be drawn with the help of set square
Drawing Parallel Lines Using the Set Square
1. Draw a line l and mark a point outside the line.
2. Place any side of the set square forming the right angle along line l.

Drawing a Line
3. Place a ruler along the other side of the set square to form a right angle as shown.
The line must be fixed.

Place a Ruler Alongside
4. Slide the set square along the ruler upwards such that point O lines along the arm of the set square.
5. Remove the ruler and draw a line along the given line. Name this line m.
m is the desired line parallel to l. m|| l.

Drawing Parallel Lines
Solved Examples
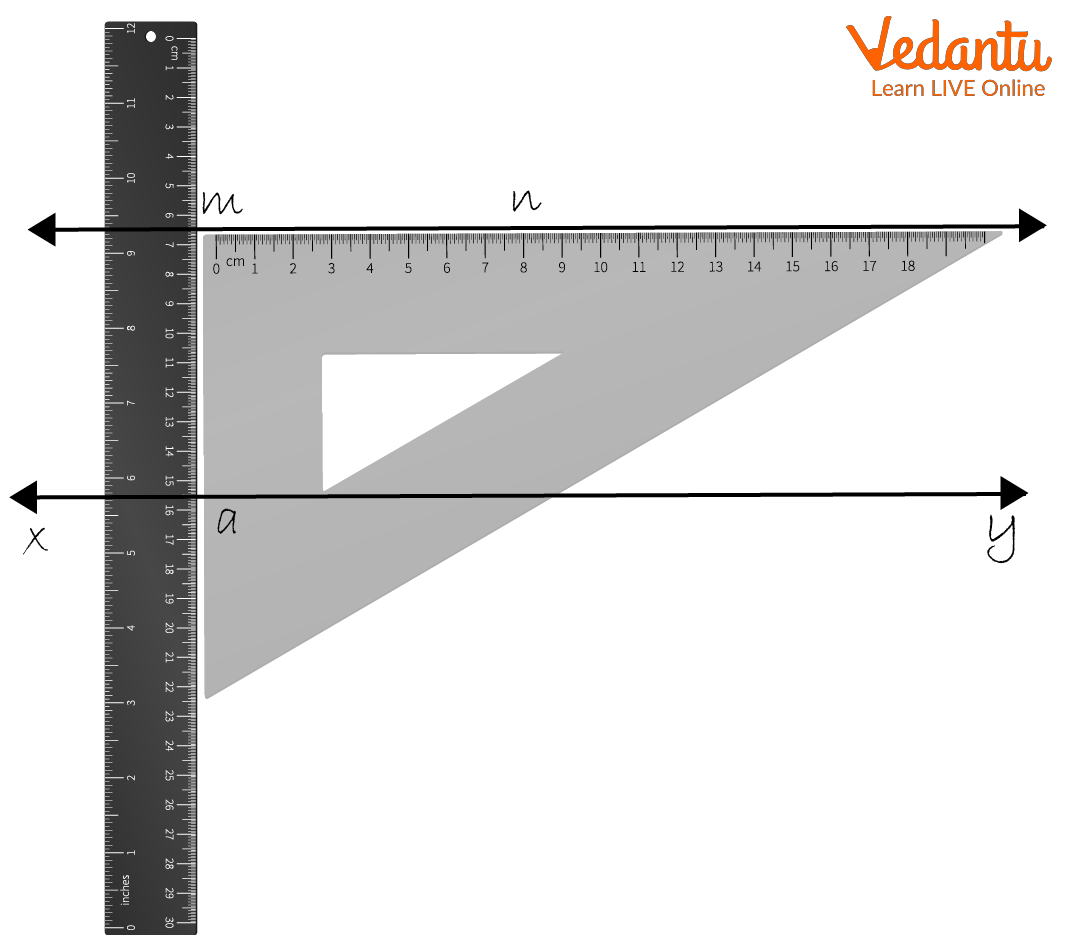
Using a square and ruler, draw a line parallel to this line way through the 5cm point above.
(i) Use a ruler to draw an \[{\rm{XY}}\] line and mark point A on it.
(ii) Draw \[{\rm{AM}} = 5\]cm using a square.
(iii) Place the given square on the \[{\rm{XY}}\] segment.
(iv) While holding the straightedge firmly along \[{\rm{AM}}\] move the rectangle along the straightedge until the edge of the rectangle touches point M
(v) Draw a line \[{\rm{MN}}\] along the edge through M.
(vi) \[{\rm{MN}}\] is the desired line from M parallel to \[{\rm{XY}}\].
Drawing Parallel Lines
Conclusion
The cross-arm of a T-square, which is typically perpendicular to the paper and is oriented at a specified angle, or another solid, level bottom line, must be placed on one side of the desired angle. Then, it's common practice to mark off with a pencil or pen the other edge of the agreed angle.
FAQs on How to Draw Parallel Lines with a Set Square
1. What is a set square and why is it used in geometry?
A set square is a triangular drawing instrument used in geometry and technical drawing. They typically come in two forms: a 45-90-45 degree triangle and a 30-60-90 degree triangle. Their primary purpose is to help draw lines with precision, especially for constructing parallel and perpendicular lines using their straight edges as a guide against a ruler or another set square.
2. What are the step-by-step instructions for drawing a line parallel to a given line using a ruler and a set square?
To draw a parallel line using a ruler and a set square, follow these exact steps:
Place the ruler on the paper to serve as a fixed track.
Align one of the edges of the set square perfectly with the original line.
Press the ruler firmly against another edge of the set square, creating a base.
Holding the ruler steady, carefully slide the set square along the ruler's edge to the position where you want the new line.
Draw the new line along the same edge of the set square. This new line will be perfectly parallel to the original.
3. How can you draw parallel lines using two set squares instead of a ruler?
Yes, using two set squares is a common technique. One set square acts as the base while the other slides. The method is as follows:
Place one set square on the paper to act as a fixed base.
Align an edge of the second set square with the original line you want to copy.
Bring the first set square (the base) up to meet an edge of the second set square.
Hold the base set square firmly and slide the second set square along its edge to the new position.
Draw your new line along the guiding edge of the sliding set square.
4. What are the key properties of parallel lines that are important for their construction?
The most crucial property is that parallel lines maintain a constant perpendicular distance from each other and never intersect. For construction, we use the concept of a transversal line. By sliding a set square along a straight edge (the transversal), we ensure that the corresponding angles formed are always equal. According to geometry rules, if the corresponding angles are equal, the lines must be parallel.
5. Can a set square be used to draw a parallel line at a specific, predetermined distance?
Yes, a parallel line can be drawn at a specific distance using a set square and a marked ruler. First, use the 90-degree corner of the set square to draw a perpendicular line intersecting your original line. Use the ruler to measure the desired distance along this perpendicular line and make a mark. Finally, place the set square on this new mark and use the standard sliding method to draw a line parallel to the original, ensuring it passes through the marked point.
6. What is the main principle that allows a set square to create perfectly parallel lines when slid along a ruler?
The principle is based on maintaining a constant angle. The ruler acts as a fixed reference line or a transversal. When you slide the set square along the ruler without rotating it, you are essentially moving the triangle while keeping its orientation fixed. The edge you draw along, therefore, always makes the same angle with the ruler. In geometry, when two lines are crossed by a transversal and the corresponding angles are equal, the lines are defined as being parallel.
7. How does drawing parallel lines with a set square differ from drawing them with a compass and ruler?
The main difference is the tool and the underlying geometric proof being applied:
Set Square Method: This is a mechanical method that relies on sliding a tool to physically transfer an angle. It is based on the corresponding angles postulate and is generally faster for quick drafting.
Compass and Ruler Method: This is a classical construction method. It relies on creating arcs to construct congruent alternate interior angles or a rhombus, proving the lines are parallel based on fundamental geometric axioms. It is considered a more formal and foundational construction in Euclidean geometry.
8. What common mistakes should students avoid to ensure lines drawn with a set square are truly parallel?
To ensure accuracy, avoid these common errors:
Slipping Base: The most frequent mistake is letting the ruler or base set square move. It must be held down securely.
Worn-out Tools: Using a set square with nicks or worn edges will result in a non-straight line.
Pencil Thickness and Angle: An inconsistent pencil angle or a very thick pencil tip can introduce inaccuracies in the line's position.
Initial Misalignment: Failing to align the set square perfectly with the original line at the start will cause the final line to be skewed.

















