




How to Calculate the Area of a Quarter Circle with Examples
What Is a Quarter Circle?
The portion of the area formed by two radii of the circle that are perpendicular to each other is called a quarter of a circle. Hence, the one-fourth area/portion of the circumference of a circle is a quarter circle. It is also known as a quadrant or a quadrant of a circle. So, in clear words, we can say that if we divide a circle into four equal parts, each part is a quarter circle or a quadrant. The image of a quarter of a circle is given below.
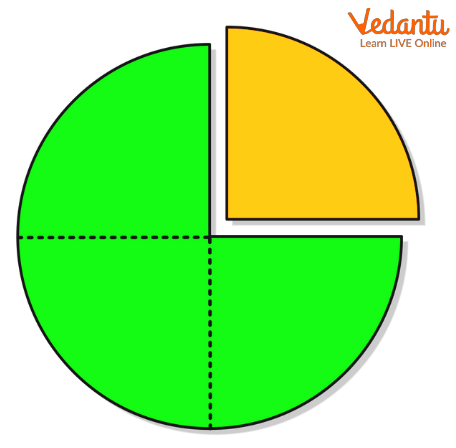
A Quarter of a Circle
Formulae for Calculating the Area of a Quarter Circle
Now we will derive a formula to calculate the area of a quarter of a circle. Let’s take a circle whose radius is 'r' and diameter 'd'. So we know that d = 2r. Now we can derive the formulae for the area of a quarter circle in terms of radius and diameter.
1. Calculation of the area of a Quarter Circle using Radius
We have studied that the area of a circle is calculated by πr2. Now, we already know that a quarter circle is one-fourth portion of a full circle. Thus, the area of the quarter circle is one-fourth of the area of the circle.
Hence, the area of a quarter circle in terms of radius = πr2 / 4
2. Calculation of the area of a Quarter Circle using Diameter
We know that d = 2r, then r = d/2. Now, we will substitute this in the above formula of calculation of the area of a quarter circle in terms of radius and we will get the area of a quarter circle in terms of diameter.
Hence, the area of a quarter circle in terms of diameter= π(d/2)2/ 4
The area of ¼ of a circle in terms of diameter = πd2 / 16
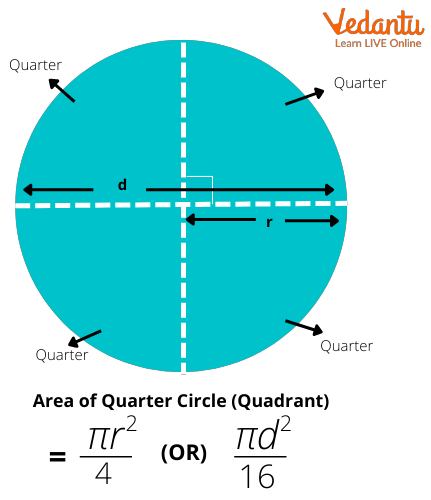
Area of a Quarter Circle in terms of radius and diameter
Solved Examples
Example 1: The radius of a circular park is 60 metres. A quarter circular portion of this part is used for doing exercise for old people. Find the area of the portion that is used by the old people for exercise. Use π = 3.142.
Solution: The radius of the circular park is given, r = 60 metres.
The area of the portion used by the old people for exercise can be calculated with the help of the formula of the area of a quarter circle.
The portion of the park used by the old people for exercise= πr2 / 4 = (3.142)(60)2 / 4 = 2827.8 square metres.
Answer: The required area used by the old people for exercise is 2827.8 square metres.
Example 2: Rohan ordered a pizza for himself and his three friends. They want to share it equally. The pizza is circular shaped and its diameter is 32 centimetres. Find the amount of pizza that each of them will get. Use π = 3.14.
Solution: The diameter of the pizza is given, d = 32 centimetres.
Since it is mentioned in the problem statement that the pizza is divided into four equal parts, each part is a quarter circle and hence its area can be calculated with the help of the formula of the area of a quarter circle formula.
The radius of the pizza is r = d/2 = 32/2 = 16 centimetres
Area of each portion = πr2 / 4 = (3.14)(16)2 / 4 = 200.96 square centimetres.
Hence the amount of pizza that each of them will get will be 200.96 square centimeters.
Conclusion
In this article, a quarter of a circle is discussed in simple language. The formulae for the calculation of a quarter of a circle are also given. The formulae are provided in terms of radius as well as diameter.
FAQs on Area of a Quarter Circle: Step-by-Step Guide for Students
1. What is a quarter circle?
A quarter circle is a sector of a circle that covers exactly one-fourth of the circle's total area. It is formed by two radii positioned at a 90-degree angle to each other at the circle's centre. This shape is also commonly referred to as a quadrant.
2. What is the formula to calculate the area of a quarter circle?
The formula for the area of a quarter circle is Area = (1/4)πr². In this formula, 'r' represents the radius of the circle, and π (pi) is a mathematical constant, approximately equal to 3.14 or 22/7. This formula essentially calculates the area of the full circle (πr²) and then divides it by four.
3. How do you find the area of a quarter circle in simple steps?
To find the area of a quarter circle, follow these steps:
- Step 1: Identify the length of the radius (r) of the circle.
- Step 2: Square the radius by multiplying it by itself (r x r = r²).
- Step 3: Multiply the result by the value of pi (π), which is typically 3.14.
- Step 4: Divide the final result by 4 to get the area of the quarter circle. The answer will be in square units (e.g., cm², m²).
4. Why is the area of a quarter circle calculated by dividing the full circle's area by four?
A full circle encompasses a 360-degree angle. A quarter circle, or quadrant, is a sector with a central angle of 90 degrees. Since 90 degrees is exactly one-fourth of 360 degrees (90°/360° = 1/4), the space it occupies (its area) is also precisely one-fourth of the total area of the circle. This proportional relationship is why we simply divide the full circle's area formula (πr²) by 4.
5. What is the difference between the area and the perimeter of a quarter circle?
The key difference lies in what they measure:
- Area refers to the amount of two-dimensional space inside the quarter circle's boundaries. It is measured in square units (like cm²).
- Perimeter refers to the total length of the boundary of the shape. For a quarter circle, this includes the curved arc and the two straight sides (radii). It is calculated as (πr/2) + 2r and is measured in linear units (like cm).
6. Can you provide a real-world example of calculating the area of a quarter circle?
Imagine you are designing a garden in a square corner of your backyard. If you plan a flower bed in the shape of a quarter circle with a radius of 7 feet, you would need to calculate its area to know how much soil and how many seeds to buy. Using the formula Area = (1/4)πr², the area would be (1/4) * (22/7) * (7)² = 38.5 square feet.
7. How does doubling the radius affect the area of a quarter circle?
Doubling the radius of a quarter circle does not double its area; it quadruples it. This is because the area formula depends on the square of the radius (r²). For example, if a quarter circle has a radius of 5 cm, its area is (1/4)π(5²) = 6.25π cm². If you double the radius to 10 cm, the new area becomes (1/4)π(10²) = 25π cm², which is four times the original area.

















