




How to Solve Division Without Regrouping: Examples & Tips
Overview of Division
Have you ever heard about solving a division problem without regrouping? If not, then do not get tense because you have reached the right place. In this writing, we are going to discuss division without regrouping, division steps, and division without remainders. Division is a mathematical operation that is used to divide a number into several equal parts to obtain its solution. Generally, it is represented using the symbol '÷' or '/' in between the two numbers. Now, let us start with our topic.
What is Division without Regrouping?
Division without regrouping is defined as a process of dividing a number by another number without rearranging or regrouping it. The quantity being divided is called the dividend and the number which is dividing the dividend is called the divisor.
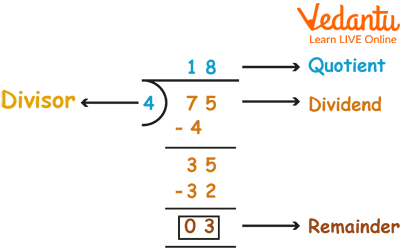
Division
Long Division Method without Regrouping and without Remainder
The long division method without regrouping and without remainder is very similar to that of the ordinary long division method. The only difference is that in the ordinary long division method, the remainder, r lies between 0 and one less than the divisor. The remainder will always be 0.
Division Steps
In order to perform division, we need to understand a few steps. The divisor is separated from the dividend by a right parenthesis 〈)〉 or vertical bar 〈|〉 and the dividend is separated from the quotient by a vinculum (an overbar). Now, let us follow the steps of the long division given below to understand the process.
Step 1: Take the first digit of the dividend from the left. Check if this digit is greater than or equal to the divisor.
Step 2: Then divide it by the divisor and write the answer on top as the quotient.
Step 3: Subtract the result from the digit and write the difference below.
Step 4: Bring down the next digit of the dividend (if present).
Step 5: Repeat the same process.
Solved Examples Based on Division Without Remainders
Q1. 900 ÷ 5
Ans: Let us divide this using the following steps.
Step 1: We will consider the first digit of the dividend and it by 5 . Here it will be $9 \div 5$.
Step 2: Now, 9 is not divisible by 5 but $5 \times 1=5$, so write 1 as the first digit in the quotient.
Step 3: Write 5 below 9 and subtract $9-5=4$.
Step 4: Since $4<5$, we will bring down 0 from the dividend to make it 40.
Step 5: 40 is divisible by 5 and we know that $5 \times 8=40$, so, write 8 in the quotient.
Step 6: Write 40 below 40 and subtract $40-40=0$.
Step 7: Bring down the next $O$ from the dividend. Since $5 \times 0=0$, we write $\mathrm{O}$ as the remaining quotient.
Step 8: Therefore, the quotient $=180$ and no remainder is left after the division, that is, remainder $=0$.
Hence, the long division technique without regrouping and without remainder yields 180 as a quotient.

Division without regrouping
Q2. 848 ÷ 4
Ans: Division steps to calculate the result of the given division problem are:
Step I: Begin with the hundreds digit i.e. 8 hundreds $\div 4=2$ hundreds.
Step II: Now bring down tens digit, i.e. 4 tens $\div 4=1$ ten
Step III: Then bring down ones digit, i.e. 8 ones $\div 4=2$ ones
Therefore, $848 \div 4=212$
Hence, the quotient and remainder obtained on the division of 848 and 4 are 212 and 0 respectively.

Division without remainders
Practice Problems
Q 1. Divide without regrouping 848 and 4.
Ans: 212
Q 2. Divide 459 by 9.
Ans: 51
Q 3. Solve 480 ÷ 24
Ans: 20
Q 4. Evaluate the division problem: 312 ÷ 3
Ans: 104
Q 5. Find 674 by 2
Ans: 337
Summary
To wrap up here with the topic of division without regrouping. It is defined as the division of a number without regrouping. The main objective of this article is to impart knowledge of division to students, by covering every topic including, the long division method without regrouping and without remainder and division steps. This writing covers numerous solved examples along with the use of images to make learning interesting and creative. Some unsolved practice problems are also given for practice. I Hope you enjoyed reading and learning about it.
FAQs on Division Without Regrouping Made Easy
1. How many types of divisions are there?
There are four types of division, namely:
Division using Repeated Subtraction
Division on a Number Line
Short division method
Long Division Method
2. Can one perform repeated subtraction at the place of division?
Yes, one can perform repeated subtraction at the place of division because the meaning of both terms is the same. For example: when we divide the number 12 by 4, we get 3 as the quotient and 0 as the remainder i.e. 12 ÷ 4 = 3. In the same way, if we subtract 4 from 12, three times, we will get the result 0.
3. How do you find the value of the divisor if the value of dividend, quotient and remainder is given?
It is quite easy to find the divisor with the help of dividend, quotient, and remainder using the given formula:
Dividend = (Divisor × Quotient) + Remainder
Divisor = (Dividend - Remainder) / Quotient
Put the given values in the above formulas, you will get the value of the divisor.























