Rules of Division of Integers

Mathematicians use addition, subtraction, division, and multiplication to perform arithmetic operations on all various areas of real numbers, including natural numbers, integers, and rational numbers. A division of integers is a process of dividing integers. When an integer is divided, it is usually evenly divided into groups or divided into a specified number of groups. Here, in this article, students will learn about the definition of dividing integers, and about what is the rule for dividing integers. Some examples are also discussed by applying the learning.

Division of Integers

Integer division works by dividing an integer value into equal parts. The division consists of three parts. The value that has been divided into equal groups is called the dividend. The value that divides into equal groups is known as the divisor. Additionally, the answer obtained is called the quotient, which clarifies how many components are divided into equal groups.

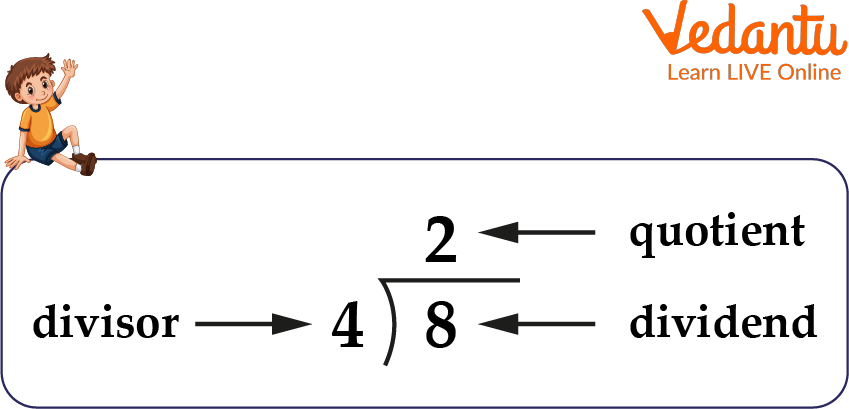
Division of Integers

What are the Rules for Dividing Integers?

Here we have listed some rules that are to follow while dividing integers:

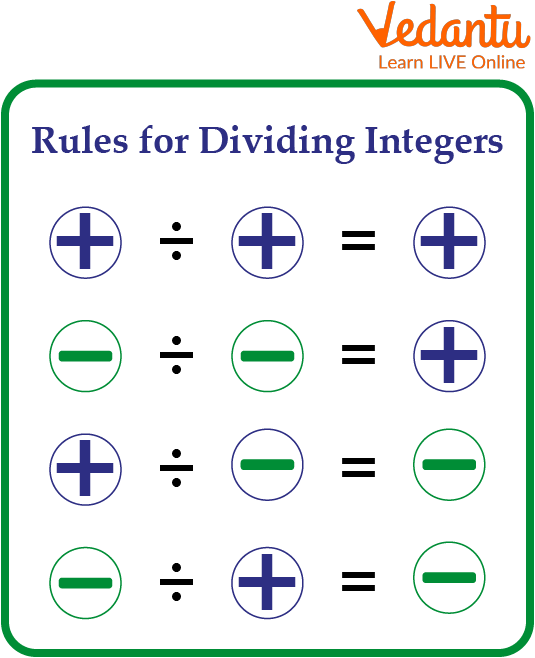
Rules of Division of Integers

Rule 1: To divide two numbers with similar signs, we divide their values and add a plus sign to the quotient.

Here, we divide two positive integers that have a positive quotient.

$\dfrac{(+9)}{(+3)}=+3$

Here, we divide two negative integers that have a positive quotient.

$\dfrac{(-9)}{(-3)}=+3$

Rule 2: To divide integers with opposite signs, we, therefore, divide their values and add a minus sign to the quotient.

$\dfrac{(+16)}{(-4)}=-4$

Properties of Division of Integers

By learning the definition of dividing integers, we got to know about the following characteristics of integer division:

• If $x$ and $y$ are integers, then $x \div y$ is not always an integer. For instance, the numerals $17 \div 3$ and $-19 \div 6$ are not.

• If $\mathrm{x}$ is an integer other than $0, \mathrm{x} \div \mathrm{x}$ equals 1 .

• We have $x \div 1=x$ for every integer $x$.

• If $\mathrm{x}$ is an integer greater than zero, then $0 \div x=0$.

• If $x$ is an integer, $x \div 0$ has no significance.

• Unless $z=1$, if $x, y$, and $z$ are non-zero integers, then $(x \div y) \div z \neq x \div(y \div z)$.

Solved Examples of Dividing Integers

Example 1: Solve $-91 \div 7$

Solution: We have, $-91 \div 7$

Using the divisibility rule of 7 i.e. if a number is divisible by 7, then “the difference between twice the unit digit of the given number and the remaining part of the given number should be a multiple of 7 or it should be equal to 0”. So 91 is divisible by 7.

We know that 91 is divisible by 7, as both the numbers have opposite signs, so negative sign will come with the quotient, i.e.

= $\dfrac{-91}{7}$

= -13

Thus, the result of the division of -91 and 7 is -13.

Example 2: Solve $117 \div 3$

Solution: We have $117 \div 3$

Using the divisibility rule of 3, we know that 117 is divisible by 3.

As both the numbers have the same signs, so positive sign will come with the quotient, i.e.

= $\dfrac{117}{3}$

= 39

Thus, the result of the division of 117 and 3 is 39.

Practice Problems

1. Solve the following

1. $\dfrac{(+8)}{(+4)}=$

2. $\dfrac{(-9)}{(-3)}=$

3. $\dfrac{(+84)}{(+4)}=$

4. $\dfrac{(-49)}{(-7)}=$

Ans:

a. +2

b. +3

c. +21

d.+7

2. Fill in the blanks

1. 296 ÷ ……………. = -148

2. -88 ÷ ……………. = 11

3. 84 ÷ ……………. = 12

4. ……………. ÷ -5 = 25

Ans:

a. -2

b. -8

c. 7

d. -125

Summary

In this article, we reviewed the definition of dividing integers and then used examples to clarify how to divide integers. It's going to be easier to quickly solve the questions with the help of the learned rules and properties. The above writing explains deeply what is the rule for dividing integers. There are two rules for dividing integers. The result will be positive if both of the integers are negative or positive and the result will be negative if one integer is positive and the other is negative. Solved Examples of Dividing Integers and practice questions that have been provided in this article will help you in understanding how to divide integers.