




How to Read and Use a Coordinate Grid in Maths
What is a Coordinate Plane?
A coordinate plane is a two-dimensional surface made up of two number lines. It is formed when a horizontal line known as the X-axis and a vertical line known as the Y-axis intersect at the origin. Points are located using the numbers on a coordinate grid. A coordinate plane is useful for graphing points, lines, and other objects. It functions as a map, providing precise directions from one point to another.
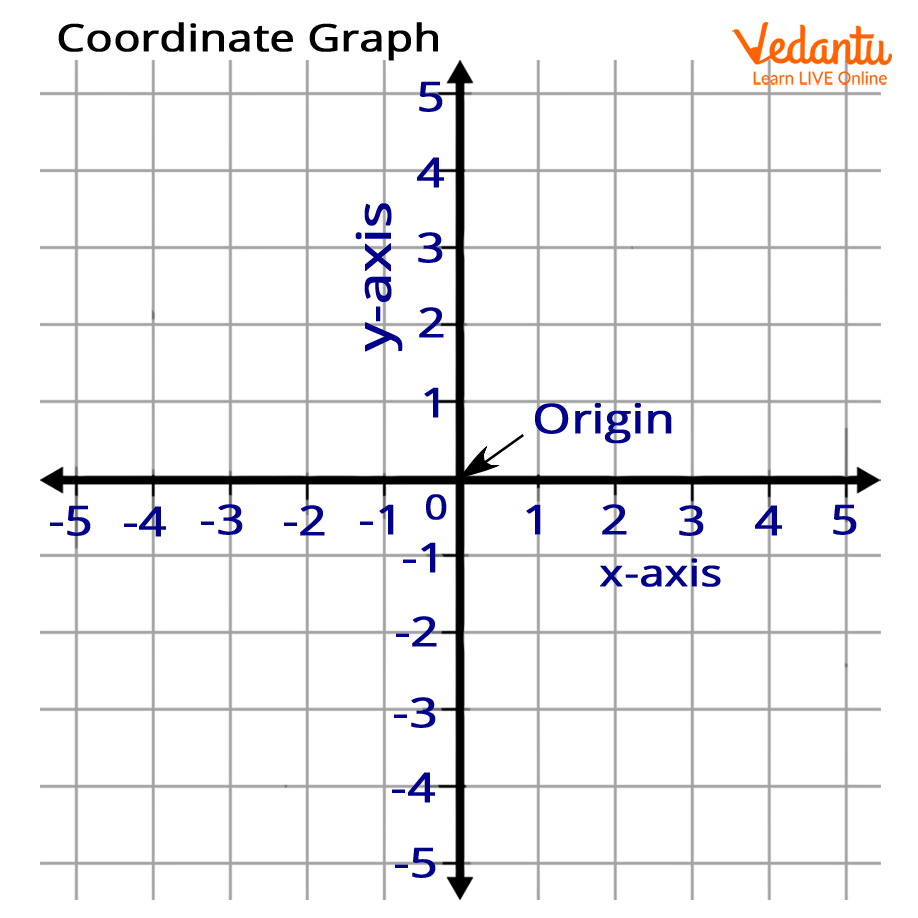
Description of a Coordinate Plane
In this section, we will learn about the components of a coordinate plane.
Axis - There are two axes in a coordinate plane. The horizontal line is called the x-axis and the vertical line is called the y-axis.
Quadrant - The four equal divisions by origin are known as the quadrants. They are known as Quadrant I, Quadrant II, Quadrant III, and Quadrant IV.
Quadrant I - This quadrant comes in the positive - positive part, i.e., the x-axis is positive and the y-axis is also positive.
Quadrant II - This quadrant comes in the negative - positive part, i.e., the x-axis is negative and the y-axis is positive.
Quadrant III - The third quadrant comes in the negative - negative part, i.e., both the x-axis and y-axis are negative.
Quadrant IV - The fourth quadrant comes in the positive - negative quadrant, i.e., the x-axis is positive and the y-axis is negative.
Positive x-axis - The horizontal line towards the right from the origin is the positive x-axis.
Negative x-axis - The horizontal line towards the left from the origin is the negative x-axis.
Positive x-axis - The vertical line above the origin is the positive y-axis.
Negative x-axis - The vertical line below the origin is the negative y-axis.
Coordinates - The points that are located on the x and y axes or the coordinate graph are called the coordinates. It is always written in a particular format, which is (x,y).
Here is an image to understand the coordinate graph in a better way:
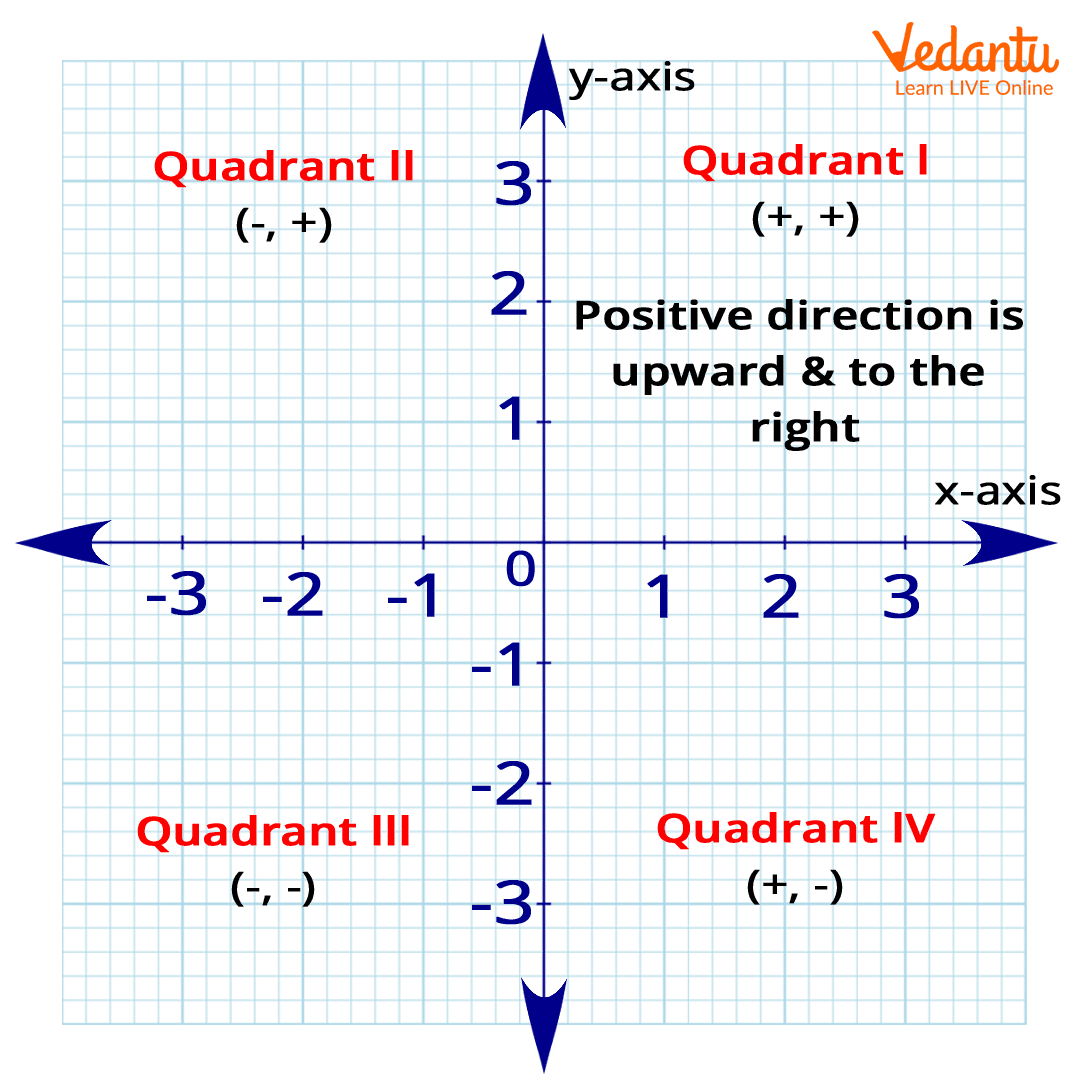
How to Locate a Point on the Coordinate Plane?
Here is the step by step explanation of locating a point on the coordinate plane:
Read the point carefully.
Find the quadrant by checking the sign of the coordinates. For example - (2,3) will be on the quadrant I, (-4,5) will be on quadrant II, (-3,-2) will be on the quadrant III, and (6,-3) will be on the quadrant IV.
Once you have found the coordinate, locate the point on the x-axis on the right quadrant. For example - Point A on the first quadrant has coordinate 3 on the x-axis.
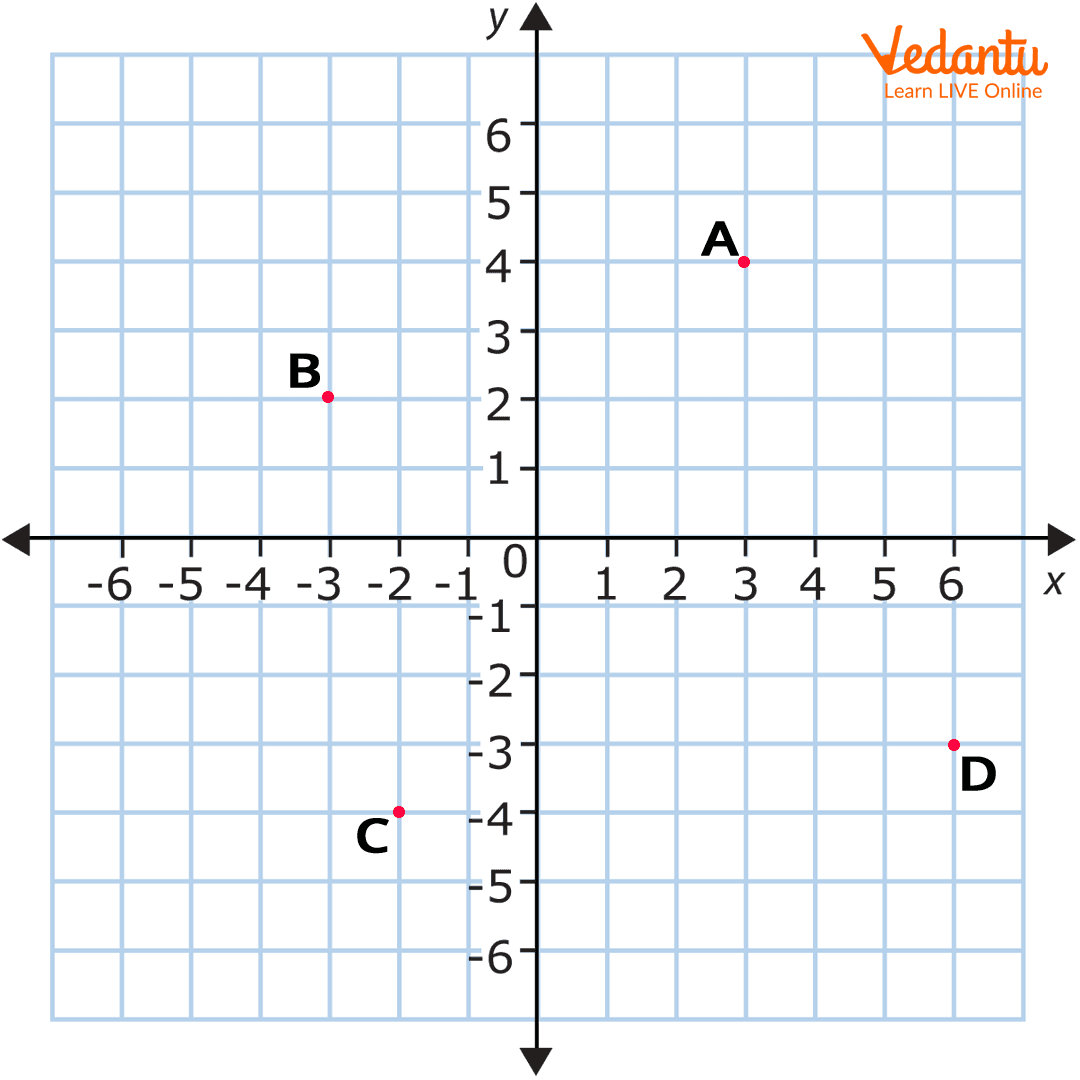
Similarly, locate the point on the y-axis on the right quadrant. For example - On the above image, point A on the first quadrant has coordinate 4 on the y-axis.
The point is located. For the above image, point A has the coordinate of (3,4).
How to Draw the Coordinate Graph?
Here is the step by step explanation of how to draw the graph:
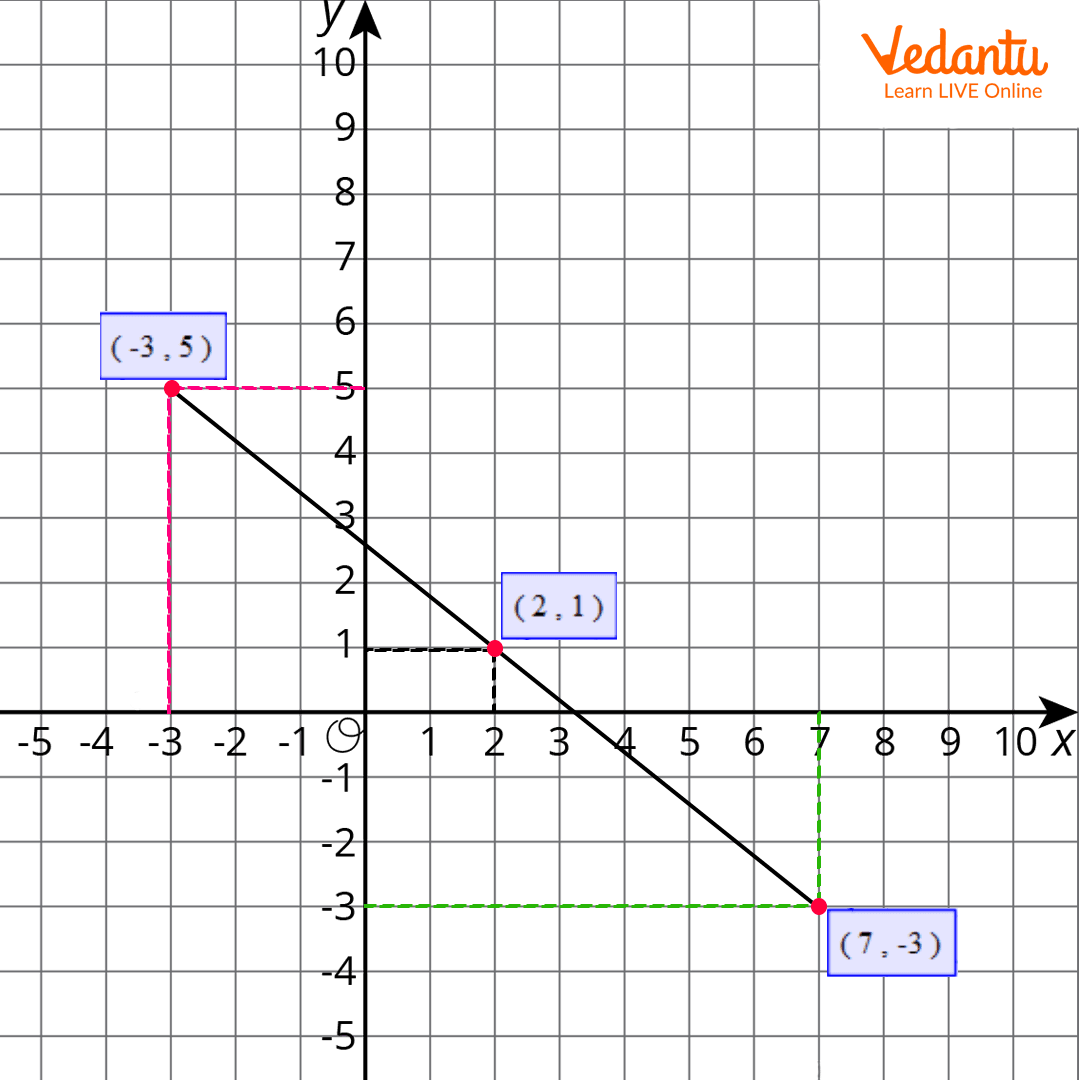
Let us consider the following points: (-3,5), (2,1), and (7,-3)
Identify the quadrants of the coordinates. For the first coordinates (-3,5), the quadrant will be quadrant II, for the second coordinates (2,1), the quadrant will be quadrant I, and for the third coordinates (7,-3), the quadrant will be quadrant IV.
Find the points on the right quadrant on the x-axis and y-axis.
Join the points to form a straight line.
Consider the following image for your reference:
Quick Fact
The coordinate plane was introduced by French mathematician René Descartes. It is after his name that coordinate plane is also called Cartesian coordinate system. |
Conclusion
So far you have learned about the coordinate graph, about its components, how to locate a point on the coordinate graph, and how to draw the graph. If you want to know more details about the coordinate graphs and solve exercises, you can explore more on our website. Apart from the coordinate graphs, we have covered all other mathematical topics. So you can explore them anytime on our website and enjoy learning!
FAQs on Coordinate Grid Explained for Students
1. What is a coordinate grid and what is it used for in mathematics?
A coordinate grid, also known as a Cartesian plane or coordinate plane, is a two-dimensional plane formed by the intersection of two perpendicular number lines. These lines, called axes, are used to precisely locate points. The primary use of a coordinate grid is to provide a visual link between geometry and algebra, allowing us to graph equations and geometric shapes.
2. What are the essential components of a coordinate grid?
A coordinate grid is made up of several key components that work together to define locations:
The x-axis: The horizontal number line that runs from left to right.
The y-axis: The vertical number line that runs from top to bottom.
The Origin: The point where the x-axis and y-axis intersect. Its coordinates are (0, 0).
Quadrants: The four regions that the axes divide the plane into.
3. How do you correctly write the coordinates for a point on a grid?
Coordinates are always written as an ordered pair in the format (x, y). The first number, the x-coordinate (or abscissa), tells you the horizontal distance from the origin. The second number, the y-coordinate (or ordinate), tells you the vertical distance from the origin. For example, the point (4, 5) is located 4 units to the right of the origin and 5 units up.
4. Can you provide an example of how to plot a point on a coordinate grid?
Certainly. To plot the point (3, 2), you would follow these steps:
Start at the origin (0, 0).
Look at the x-coordinate, which is 3. Move 3 units along the horizontal x-axis to the right (since it's positive).
From that position, look at the y-coordinate, which is 2. Move 2 units up parallel to the vertical y-axis (since it's positive).
Mark this final location with a dot. This is the point (3, 2).
5. Why is the x-coordinate always written before the y-coordinate in an ordered pair?
The x-coordinate is always written first as a matter of mathematical convention. This standardisation ensures that anyone reading the coordinates will interpret them the same way, avoiding confusion. Because the order matters, the pair (x, y) is called an 'ordered pair'. For example, the point (2, 3) is in a completely different location from the point (3, 2). This consistent order is fundamental for correctly graphing and interpreting data.
6. What are the four quadrants of a coordinate grid and their sign conventions?
The x and y axes divide the coordinate plane into four regions called quadrants. They are numbered counter-clockwise starting from the top right:
Quadrant I: Top right. Here, both x and y are positive (+, +).
Quadrant II: Top left. Here, x is negative and y is positive (–, +).
Quadrant III: Bottom left. Here, both x and y are negative (–, –).
Quadrant IV: Bottom right. Here, x is positive and y is negative (+, –).
7. What is the importance of the origin in a coordinate grid?
The origin, located at (0, 0), is critically important because it serves as the universal reference point for all locations on the grid. Every coordinate is a measurement of distance and direction from the origin. Without the origin, there would be no fixed starting point to measure from, making it impossible to uniquely identify any point on the plane.
8. What happens if a point lies directly on an axis instead of in a quadrant?
If a point lies directly on an axis, it does not belong to any quadrant. Its coordinates will have a zero value.
If a point lies on the x-axis, its vertical distance from the origin is zero, so its y-coordinate is 0. The format is (x, 0).
If a point lies on the y-axis, its horizontal distance from the origin is zero, so its x-coordinate is 0. The format is (0, y).
9. How is the concept of a coordinate grid applied in the real world?
The coordinate grid is a fundamental concept with many real-world applications. For instance, it's the basis for GPS and mapping systems, where latitude and longitude act as coordinates to pinpoint locations on Earth. It is also used in computer graphics and video games to position characters and objects on a screen, and in data science to create graphs that show relationships between two variables.























