Ascending Order in Fraction

We can say that fraction is a number expressed as a quotient in which there are two numbers: a numerator and a denominator which are dividends. We can also say that fractions represent a part of a whole. A fraction has two parts, namely numerator, and denominator. The numerator is the number that is on the top and the denominator is the number that is at the bottom. Let's take a fraction $\dfrac{1}{8}$. In this 1 is on top so it is the numerator and 8 is at the bottom so it is the denominator. Let us understand fractions with some other examples.

Fraction Showing 1 Part of Pizza Out of 8 Parts

Now let us understand how to arrange these fractions in ascending order.

Arranging Fractions in Ascending Order

To arrange ascending order in fractions we have to convert the given fractions into like fractions if the fractions are not already in like a fraction.

Like fractions of those fractions that have the same denominator.

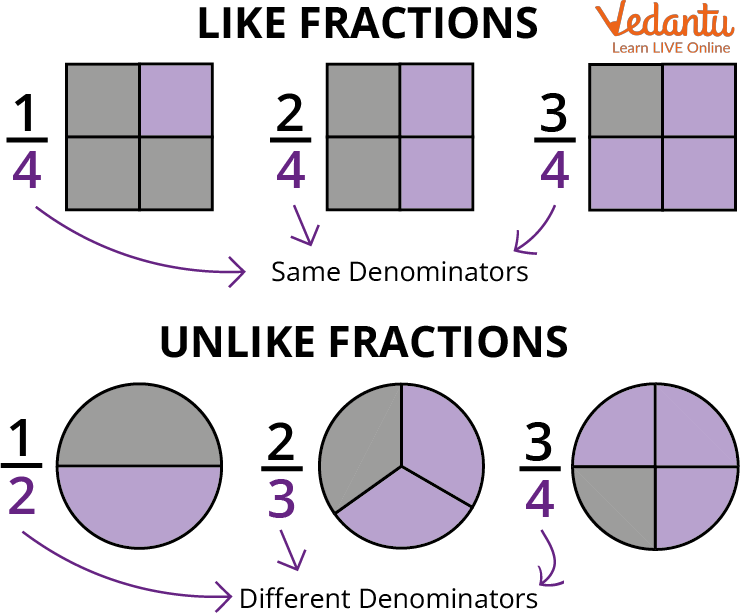
Like Fractions and Unlike Fractions.

Example: Arrange $\dfrac{14}{40}$, $\dfrac{27}{40}$, $\dfrac{3}{40}$, and $\dfrac{33}{40}$ in ascending order.

Ans: In this situation, we can say that every fraction has the same denominator which is 40 which means they are like fractions.

Now, all we have to do is focus on the numerator. Now, all we have to do is arrange these numerators in ascending order. In this case, we have four numerators - 14, 27, 3, 33

Since 3< 14< 27< 33

Therefore $\dfrac{3}{40}$ < $\dfrac{14}{40}$ < $\dfrac{27}{40}$ < $\dfrac{33}{40}$.

Let's take another example,

Example: Convent $\dfrac{1}{3}$, $\dfrac{3}{5}$, and $\dfrac{1}{2}$ in Ascending order.

Ans: These fractions are clearly unlike fractions because they have different denominators. To convert these fractions into like fractions we have to convert their denomination for this we have to take the LCM of the denominator.

In this case, we have to take LCM of 3, 5, and 2.

LCM of 3,5,2= 30

Now since the LCM of 3, 5, and 2 is 30 we have to convert the denominator of all the numbers to 30.

Now to make the fraction like fractions we have to divide the L.C.M. by the denominator of fractions, then multiply both the numerator and denominator of the fraction with the resulting number that we get after dividing L.C.M

The first number is $\dfrac{1}{3}$. To convert 3 into 30 we have to multiply 3 by 10. If we multiply 3 by 10 then we also have to multiply the numerator that is 1 with 10

$\dfrac{1}{3} \times \dfrac{10}{10} = \dfrac{10}{30}$

Continue the same step with the other numbers.

$\dfrac{3}{5} \times \dfrac{6}{6} = \dfrac{18}{30}$

$\dfrac{1}{2} \times \dfrac{15}{15} = \dfrac{15}{30}$

Once we get all the numbers into like fractions it is pretty easy to arrange these fractions in ascending order

In this case $\dfrac{10}{30}$ < $\dfrac{15}{30}$ < $\dfrac{18}{30}$

Therefore, $\dfrac{1}{3}$< $\dfrac{1}{2}$< $\dfrac{3}{5}$

Solved Examples

Now let us solve some questions.

Q1. Arrange the given fractions in ascending order $\dfrac{2}{9}$, $\dfrac{5}{9}$, $\dfrac{1}{9}$, $\dfrac{8}{9}$.

Ans. Since the given fractions are already in ascending order we just have to compare the numerators.

Now we can see that 1< 2< 5< 8

Therefore, $\dfrac{1}{9}$< $\dfrac{2}{9}$< $\dfrac{5}{9}$< $\dfrac{8}{9}$.

Q2. Arrange the given fractions in ascending order $\dfrac{3}{4}$, $\dfrac{5}{7}$, $\dfrac{9}{3}$, $\dfrac{2}{5}$

Ans. As we can see that the above fractions are unlike fractions. To convert them into like fractions we will have to take out the LCM of the denominators.

LCM of 4, 7, 3, and 5 is 420.

To convert the denominators of these fractions into 420

Now to make the fraction like fractions divide the L.C.M. by the denominator of fractions, then multiply both the numerator and denominator of the fraction with the resulting number after dividing L.C.M.

$\dfrac{420}{4}$= 105

Therefore, $\dfrac{3}{4} \times \dfrac{105}{105}$ = $\dfrac{315}{420}$

On repeating the steps:

$\dfrac{420}{7}$ = 60

$\dfrac{5}{7}$$\times$$\dfrac{60}{60}$ = $\dfrac{300}{420}$

Again $\dfrac{420}{3}$ = 140

$\dfrac{9}{3} \times \dfrac{140}{140}$ = $\dfrac{1260}{420}$

$\dfrac{420}{5}$ = 84

$\dfrac{2}{5} \times \dfrac{84}{84}$ = $\dfrac{168}{420}$

Converting the fractions into like fractions we have to compare the numerator of the like fraction

We can see that 168< 300< 315< 1260

Therefore,

$\dfrac{168}{420}$< $\dfrac{300}{420}$< $\dfrac{315}{420}$< $\dfrac{1260}{420}$ which makes $\dfrac{2}{5}$ < $\dfrac{5}{7}$ < $\dfrac{3}{4}$ < $\dfrac{9}{3}$.

Practice Questions

Q1. Arrange the following in ascending order $\dfrac{2}{5}$, $\dfrac{6}{5}$, $\dfrac{3}{4}$, $\dfrac{2}{3}$

Ans: $\dfrac{2}{5}$< $\dfrac{2}{3}$< $\dfrac{3}{4}$< $\dfrac{6}{5}$

Q2. Arrange the following in ascending order $\dfrac{7}{3}$, $\dfrac{6}{5}$, $\dfrac{6}{9}$, $\dfrac{5}{4}$

Ans: $\dfrac{6}{9}$< $\dfrac{6}{5}$< $\dfrac{5}{4}$< $\dfrac{7}{3}$

Summary

To arrange ascending order means to arrange numbers from a low value to a higher value. To arrange fractions in ascending order we should always convert the fractions into like fractions. Like fractions are those fractions you have the same denominator. A part of the whole thing is known as a fraction. Here you will understand what fraction is. You will be able to arrange a fraction in ascending order. Like fractions and unlike fractions are also explained with examples.