How to Perform 2s Complement Subtraction with Step by Step Examples
Would you like to know more about 2 's complement subtraction for kids? Well, then, you've come to the right place! This article will cover a 2's complement and how it works in subtraction with complements. Two binary numbers can be subtracted using the approach of the second complement. By the end of this article, you should be more confident with your ability to perform 2 's complement subtraction, including binary subtraction using 2's complement. Let's get started!
What is a 2 's Complement?
To implement this method for subtracting two binary numbers, the first step is to find the 2’s complement of the number to be subtracted from another number. To get the 2’s complement, first of all, 1’s complement is found, and then 1 is added. The addition is the required 2’s complement.
Suppose we need to find the 2’s complement of the binary number 10010. First, find 1’s complement. To find this, replace all 1 to 0 and all 0 to 1. Therefore, 1’s complement of 10010 will be 01101. Add 1 to this, and we will get the 2’s complement, i.e. 01110.
Binary Subtraction Using 2's Complement
To learn how to subtract binary numbers using 2's complement, which is the subtraction of a smaller number from a larger number using 2’s complement subtraction, the following steps are to be followed:
Step 1: Determine the 2’s complement of the smaller number
Step 2: Add this to the larger number.
Step 3: Omit the carry. Note that there is always a carry in this case.
The following example illustrates the above-mentioned steps:
Exampe: Subtract $(1010)_2$ from $(1111)_2$ using 2's complement method.
Ans:
Step 1: 2's complement of $(1010)_2$ is $(0110)_2$.
Step 2: Add $(0110)_2$ to $(1111)_2$.
This is shown below:
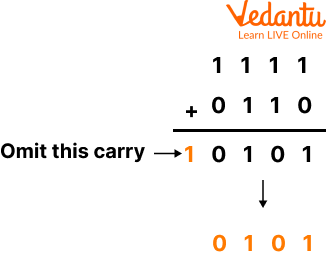
Subtract Using 2's Complement Method
To subtract a larger number from a smaller number using 2’s complement subtraction, the following steps are to be followed:
Step 1: Determine the 2’s complement of the smaller number.
Step 2: Add this to the larger number.
Step 3: There is no carry in this case. The result is in 2’s complement form and is negative.
Step 4: To get an answer in true form, take 2’s complement and change its sign.
Example: Subtract $(1010)_2$ from $(1000)_2$ using 2's complement.
Ans:
Step 1: Find the 2's complement of $(1010)_2$. It is $(0110)_2$.
Step 2: Add $(0110)_2$ to $(1000)_2$.
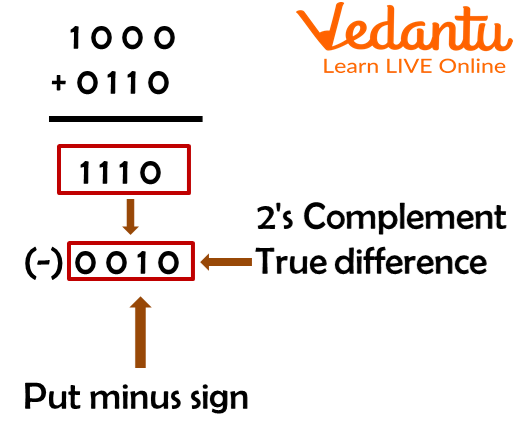
2’s complement
Step 3 and Step 4 have been explained in the above difference calculation.
Subtraction Using r's Complement:
Let's say you want to subtract the number 01010100 from 11100011. We can do this using 2 's complement by simply doing the subtraction using r's complement.
Steps to Find r's Complement:
To find r's complement, add 1 to the calculated ($r-1$) 's complement.
Here is an example:
Q. Find the 7's and 8's complement of the number $(5 63)_8$
Step 1: Identify the base (or) radix. Here $r=8$.
Step 2: Since 7 is the largest digit in the number system, subtract each digit of the given number from 7, i.e. if it's a three-digit number, subtract the number from 777.
$\therefore(214)_8$ is the 7's complement of a given number
Step 3: To find r's complement, i.e. 8's complement, then add ' 1 ' to the result of 7 's complement number.
$\therefore(215)_8$ is the 8 's complement of the given number.
Solved Examples
Q 1. 10110 - 11010
Ans: 11010 has a 2s complement of (00101+1) or 00110.
Add the 2's complement to the minuend (10110+00110) or 11100.
Now taking its complement;
The solution is (00011+1)= - (00100)
Q 2. 10110-01111
Ans: 01111's 2s complement is 10001.
The minuend plus the complement of two (10110-10001) equals 100111.
The response is 00111.
Q 3. 0100-11101
Ans: 11101's 2s complement is 00011
The minuend plus the complement of two (10100- 00011) equals 10111.
Since there is no carry here, the response is 01001.
Q 4. 110101 - 101001
Ans: 101001's complement in 2 is 010111
(110101-010111) Add the minuend and the 2's complement to get 1001100.
Carry, the result's leftmost bit is a 1 and is ignored.
The response is 001100.
Practice Questions
Q 1. 1001 - 0100
Ans: 0101
Q 2. 0100 - 1011
Ans: 1011
Q 3. 0110 - 0100
Ans: 0010
Q 4. 10110- 11101
Ans: 00111
Q 5. 110-101
Ans: 001
Summary
In conclusion, in this article, we went over two's complement subtraction. We've done an example problem to show you how it works and how it is performed on paper. The examples provided in this article are used for demonstration purposes only and thus do not necessarily model the types of problems you would encounter on a standardised test.
Instead of simply memorising the steps in this article, you should practice the problems. You can choose to use paper and pencil or use a calculator, 2 's complement subtraction calculator, or your fingers on your smartphone. Therefore, if you want to perform division (and thus subtraction) without using r's complement, you will need to learn how to use 2 's complement while performing division.
FAQs on 2s Complement Subtraction in Binary Arithmetic
1. What is 2's complement subtraction?
2's complement subtraction is a method of subtracting binary numbers by adding the 2's complement of the subtrahend to the minuend. Instead of performing direct subtraction, you convert the number to be subtracted into its 2’s complement and then perform binary addition.
- Step 1: Find the 2’s complement of the subtrahend.
- Step 2: Add it to the minuend.
- Step 3: Discard the final carry (if present).
2. How do you find the 2's complement of a binary number?
The 2's complement of a binary number is found by taking the 1's complement and adding 1 to the least significant bit (LSB).
- Step 1: Invert all bits (0 → 1, 1 → 0).
- Step 2: Add 1 to the inverted number.
1's complement → 1010
Add 1 → 1011 (2's complement).
3. Why is 2's complement used for subtraction in computers?
2's complement is used because it allows subtraction to be performed using simple binary addition circuits. Computers avoid separate subtraction hardware by converting subtraction into addition.
- Simplifies circuit design
- Handles positive and negative numbers efficiently
- Eliminates end-around carry problems
4. What are the steps to perform 2's complement subtraction?
The steps for 2's complement subtraction are convert, add, and discard carry.
- Step 1: Write both numbers with equal bit length.
- Step 2: Find the 2’s complement of the subtrahend.
- Step 3: Add it to the minuend.
- Step 4: Ignore the final carry (if present).
5. Can you give an example of 2's complement subtraction?
Yes, for example, subtract 5 − 3 using 4-bit binary.
- 5 → 0101
- 3 → 0011
- 2's complement of 0011 → 1101
- Add: 0101 + 1101 = 1 0010
6. What happens if there is no carry in 2's complement subtraction?
If there is no final carry, the result is negative and is already in 2's complement form. To find its magnitude:
- Take the 2’s complement again.
- Convert to decimal.
7. What is the difference between 1's complement and 2's complement subtraction?
The key difference is that 2's complement adds 1 to the 1's complement and does not require end-around carry adjustment.
- 1's complement: Invert bits only and add end-around carry.
- 2's complement: Invert bits and add 1, discard final carry.
8. How do you subtract a larger number from a smaller number using 2's complement?
To subtract a larger number from a smaller one, follow normal 2's complement steps and interpret the result as negative if no carry appears.
- Example: 3 − 5 (4-bit)
- 3 → 0011
- 5 → 0101
- 2's complement of 0101 → 1011
- Add: 0011 + 1011 = 1110
9. What is overflow in 2's complement subtraction?
Overflow in 2's complement subtraction occurs when the result exceeds the representable range of the given number of bits. It typically happens when adding two numbers of opposite signs gives an incorrect sign result.
- Occurs in fixed-bit systems (e.g., 4-bit, 8-bit).
- Indicated when sign bit is incorrect after operation.
10. What is the formula for 2's complement subtraction?
The formula for 2's complement subtraction is A − B = A + (2's complement of B). Instead of direct subtraction, the subtrahend is converted into its 2’s complement and added to the minuend.
- 2’s complement of B = 1’s complement of B + 1
- Discard final carry (if present)
