CBSE Physics Experiment Simple Pendulum L-T and [L-T^2] Graphs and Effective Length of Second’s Pendulum

Introduction

Almost all of us have had a pendulum clock in our homes at some point of time. It consists of a weight oscillating to and fro at regular time intervals. Some of these clocks involve the weight hanging from the clamp with a slightly shorter string, while others with a slightly longer string. What is the significance of this length, and how does it affect the period of oscillations? Let us perform a simple experiment to find out.

A Simple Pendulum is Performing a Simple Harmonic Motion

Table of Contents

• Aim

• Theory

• Observations

• Results

Aim

To plot the L-T and \[L - {T^2}\] graphs of a simple pendulum and to determine its effective length.

Apparatus Required

1. A clamp stands

2. Split cork

3. Small metallic bob with a hook

4. Cotton thread (about 100 cms)

5. Stopwatch

6. Ruler

7. Pencil

8. Graph paper

9. Sand paper

Theory

The time period T of a simple pendulum is given by the formula

\[T = 2\pi \sqrt {\dfrac{L}{g}} \]

where L = Length of the pendulum

g = Acceleration due to gravity

With g being effectively a constant (having a value \[9.81\;m{s^{ - 2}}\], we see that the time period T depends on the square root of the pendulum length L. In this experiment, we will note the time periods T of the simple pendulum as a function of different values of L and plot the graphs T and \[{T^2}\] for each value of L and study the variation. 

From the graphs, we will also try to determine the effective length L of the pendulum for a given time period T.

Procedure

1. Clean the bob carefully by using sandpaper. Tie one end of the thread to its hook and the other end to a split cork.

2. Put the clamp stand on a flat table and clamp the cork. Ensure that the length of the thread joining the cork is about 10 cm, less than half the height of the clamp stand. Measure the length of the hanging string.

3. Now with the bob hanging vertically downwards from the stand, give the bob a small pull to one side. The bob will start oscillating with small amplitude. Ensure that the bob oscillates in one plane.

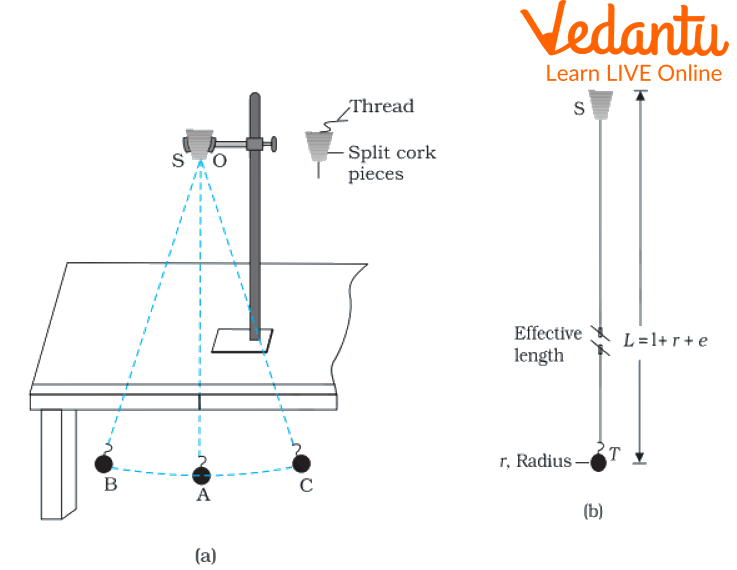
Schematic Arrangement for the Measurement of Time Period of a Simple Pendulum

4. Allow the oscillations to get steady. Count the motion of the bob from its mean position (lowest height) to the instant when it again reaches this position as one complete oscillation. Similarly, the time taken by the bob between two consecutive mean positions (or consecutive extreme positions) is known as the time period of the pendulum and is given by the above formula.

5. After about five oscillations, the motion becomes steady and we can begin noting the time periods. As the bob passes one of the mean positions, start the stopwatch and note the time taken by about 60 oscillations. Tabulate the readings.

6. Change the pendulum length from 10 cm to 20 cm. Again note the time period for 60 oscillations using a stopwatch after reaching the steady state.

7. Repeat the steps for lengths 30 cm, 40 cm and 50 cm. Measure the string lengths using a ruler. Note down the observations.

8. Plot the graphs of T and ${T^2}$ as a function of L along the X-axis in each case. Calculate the slope in both graphs.

9. From the L-${T^2}$ graph, determine the value of L for which the value of T corresponds to 2 seconds, which is the time period of a second’s pendulum. 

Observations

We’ll be noting the average time period taken by the bob for a particular length to execute 60 oscillations out of the three trials and then evaluating the time period of the pendulum in each case to complete one complete oscillation.

Observation Table

Least count of stopwatch = 

Results

Time period T for each length = \[\dfrac{\text{Time for 60 oscillations}}{{60}}\]

The time periods involve the effective length of the pendulum (length of the string + distance of the center of gravity of the bob including hook).

L-T Graph

\[T = 2\pi \sqrt {\dfrac{L}{g}}  \propto \sqrt L \]

L-\[{T^2}\] Graph

\[{T^2} = 4{\pi ^2}\dfrac{L}{g} \propto L\]

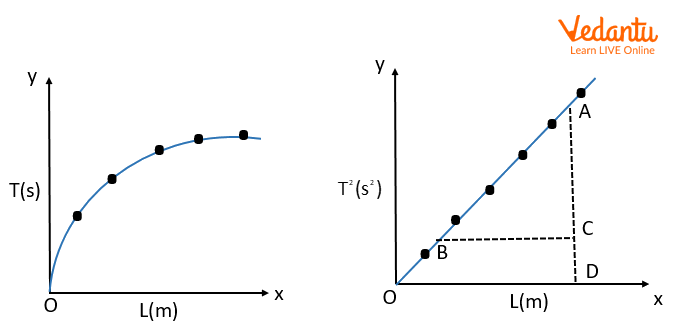
Graphs Showing the Variation of L Versus T

\[T = 2\pi \sqrt {\dfrac{L}{g}}  \to T \propto \sqrt L \]

• The graph of L versus T is parabolic in nature.

• The graph of L versus the square of T is a straight line.

• Effective length of the second’s pendulum from the $L$ versus $T^2$ graph is …………. cm.

Precautions

1. Always measure the length of the pendulum from the center of mass of the bob.

2. Always keep the amplitude of oscillations small.

3. Keep the length of the pendulum sufficiently large.

Lab Manual Questions

1. Interpret the L-T and L-${T^2}$ graphs.

Ans: The time period of a simple pendulum is given by:

$T = 2\pi \sqrt {\dfrac{L}{g}} \\$

or ${T^2} = 4{\pi ^2}\dfrac{L}{g} = \dfrac{{4{\pi ^2}}}{g}L\\$

Hence $T \propto \sqrt L \;and\;{T^2} \propto L$

So, with the graphs drawn with the x-axis as L and y-axis as T and ${T^2}$ respectively, the first graph is parabolic while the second is a straight line in shape. From the slope of the L-${T^2}$ graph, the value of acceleration due to gravity ‘g’ can be determined.

2. How does the time period change if the length becomes:

• 4 times

• 6 times

• 9 times

Ans: 

Since, \[T = 2\pi \sqrt {\dfrac{L}{g}}  \propto \sqrt L \]

Therefore for

L’ = 4L implies that T’ =\[\sqrt 4 T = 2T\]

L’ = 6L implies that T’ =\[\sqrt 6 T = 2.4T\]

L’ = 9L implies that T’ =\[\sqrt 9 T = 3T\]

3. How will you determine the value of g from the L-\[{T^2}\] graph?

Ans: Since, \[T = 2\pi \sqrt {\dfrac{L}{g}}  \to {T^2} = 4{\pi ^2}\dfrac{L}{g}\]

Hence with L taken along the x-axis and \[{T^2}\] along the y-axis, by determining the slope of the graph we can determine the value of g.

4. What is a vibratory system?

Ans: A system that undergoes continuous to-and-fro motion about a given mean position involving the mutual interconversion of kinetic and potential energies is known as a vibratory system. For e.g. a simple pendulum, a spring-mass system etc.

Viva Questions

1. What is the length of a second’s pendulum?

Ans: The length of a second’s pendulum is 99.4 cm.

2. A simple pendulum has a time period \[{t_1}\] on earth and \[{t_2}\] on the moon. Which will be finite and why?

Ans: The time period on earth \[{t_1}\] will be finite due to air resistance.

3. Explain simple pendulum theory.

Ans: A simple pendulum consists of a mass hanging from a rigid support by a strong and inextensible string. When given a little pull/ push to either side, the mass starts to execute to-and-fro motion about the mean position in one plane.

4. Explain simple pendulum graphs.

Ans: The time period of a simple pendulum is given by:

The time period of a simple pendulum is given by:

\[T = 2\pi \sqrt {\dfrac{L}{g}} \]

\[{T^2} = 4{\pi ^2}\dfrac{L}{g}\]

Hence, \[T \propto \sqrt L \;and\;{T^2} \propto L\]

So, with the graphs drawn with the x as L-axis and y as T and \[{T^2}\] axes respectively, the first graph is parabolic while the second is straight.

5. What is the acceleration due to gravity at the center of gravity of the earth?

Ans: At the center of gravity of the earth, the acceleration due to gravity g is zero.

6. Why do we keep the amplitude small?

Ans: Amplitude is kept small so that the pendulum’s motion is simple harmonic in nature and we can derive the formula of time period.

7. What is a simple harmonic motion?

Ans: The motion in which the restoring force is directly proportional to the displacement of the body from its mean position and is directed towards the mean position is known as the simple harmonic motion.

8. How are frequency and time period related?

Ans: Time period T and frequency f are related by the formula 

\[T = \dfrac{1}{f}\]

9. How much is the net force on the bob in the equilibrium position?

Ans: At the mean position, the net force on the bob is given by the difference of tension in the string and the weight of the bob.

10. Can we use a large ball as a bob of a simple pendulum?

Ans: Yes, we can use a large ball as the bob of a simple pendulum, but its weight should be less than the tensile strength of the string used for hanging, so as to prevent string breakdown. This is because the time period of a simple pendulum is independent of the mass and size of the bob.

Practical Based Questions

1. In an accelerated frame of reference, the time period T of a simple pendulum:

1. Increases

2. Decreases

3. Depends on direction of acceleration

4. Does not change

Ans: (C) In an accelerated frame of reference, the time period depends on the direction of acceleration. 

2. The period of oscillation of a simple pendulum is (pick the incorrect statement):

1. Proportional to the length of pendulum

2. Inversely proportional to g

3. Depends on mass, size and material of bob

4. Does not depend on amplitude

Ans: (C) The time period of a simple pendulum is independent of mass, size and material of the bob.

3. For m and E denoting the mass and total energy of a simple pendulum respectively, the maximum linear momentum is:

1. \[\sqrt {\dfrac{{2E}}{m}} \]

2. \[\sqrt {2mE} \]

3. \[{(2mE)^{\dfrac{3}{2}}}\]

4. \[\dfrac{1}{2}m{E^2}\]

Ans: (B) \[E = \dfrac{{{p^2}}}{{2m}}\; \to p = \sqrt {2mE} \]

4. What is the time period of a simple pendulum that takes 60 seconds to complete 30 oscillations?

1. 2 seconds

2. 0.2 seconds

3. 5 seconds

4. 0.5 seconds

Ans: (A) \[\dfrac{{60}}{{30}} = 2\,\text{seconds}\]

5) What is the approximate time period of a 1 m long pendulum?

1. 1 second

2. 2 seconds

3. 4 seconds

4. 6 seconds

Ans: (B) From the formula of time period, it will come out to be approximately 2 seconds.

6. What is the time period of a satellite orbiting the earth?

1. 24 hours

2. 48 hours

3. 30 days

4. Infinite

Ans: (A) The time period is 24 hours.

7. If the acceleration due to gravity on the surface of the earth is 6 times that on the surface of the moon, the ratio of time periods of a simple pendulum on the moon to that of on the earth is:

1. \[\dfrac{1}{{6}}\]

2. 6

3. \[\sqrt 6 \]

4. \[\dfrac{1}{{\sqrt 6 }}\]

Ans: (C) Since\[T = 2\pi \sqrt {\dfrac{L}{g}}  \propto \dfrac{1}{{\sqrt g }}\]

Given, \[\dfrac{{{g_{Earth}}}}{{{g_{Moon}}}} = 6\]

Hence, \[\dfrac{{{T_{Moon}}}}{{{T_{Earth}}}}\propto \sqrt {\dfrac{{{g_{Earth}}}}{{{g_{Moon}}}}}  = \sqrt 6 \]

8. If the mass of the bob of a simple pendulum having a time period T is doubled, then the new time period will be:

1. 2T

2. \[\sqrt 2 T\]

3. \[\dfrac{T}{{\sqrt 2 }}\]

4. T

Ans: (D) Time period is independent of the mass of the bob.

9. Out of spring and pendulum clocks, which one has the same time periods on both earth and the moon?

1. Spring clock

2. Pendulum clock

3. Both

4. Neither

Ans: (A) Spring clock has the same time period on both earth and moon.

10. The time period of a pendulum in a freely falling lift is:

1. 120 minutes

2. Zero

3. Infinite

4. 1 second

Ans: (C) The time period of a pendulum in a freely falling lift is infinite because the effective acceleration due to gravity will vanish.

Conclusion

From this experiment, we can conclude that the time period of a simple pendulum is directly proportional to its length. We also discussed various parameters affecting the same and saw how to make a simple experiment for the demonstration. 

We hope that the reader got some valuable insight regarding the concept of the simple pendulum via this article and he gets the motivation to further explore the essential applications in this topic in time to come.