NCERT Exemplar for Class 7 Maths Solutions Chapter 7 Comparing Quantities

Solved Examples

Example 1: The ratio of the heights \[1.50m\] and $75cm$ of two persons can be written as.

(a) $1:50$

(b) $1:5$

(c) $2:1$

(d) $1:2$

Ans: Correct answer is (c).

Heights ratio $=\dfrac{{{h}_{1}}}{{{h}_{2}}}$

${{h}_{1}}=1.50m$

${{h}_{2}}=75cm$……(1)

${{h}_{2}}$ in metre divide by $100$

${{h}_{2}}=\dfrac{75}{100}=0.75m$

Ratio$=\dfrac{{{h}_{1}}}{{{h}_{2}}}=\dfrac{1.50}{0.75}$

$\dfrac{{{h}_{1}}}{{{h}_{2}}}=\dfrac{150}{75}$

$\dfrac{{{h}_{1}}}{{{h}_{2}}}=\dfrac{2}{1}$

Height ratio $=2:1$

Example 2: Out of $50$ children in a class $20$ are boys, then percentage of girls.

(a) $60$

(b) $30$

(c) $50$

(d) $66\dfrac{2}{3}$

Ans: Correct answer is (a).

The total children in class $=50$

No. of boys$=20$

No. of girls $=50-20=30$

Percentage of girls $=\dfrac{\text{No. of girls}}{\text{Total students}}\times 100$

$=\dfrac{3}{5}\times 10$

$=60\%$

Example 3: The interest on $5000$ at the rate of $15\%$ per annum for one month is

(a) Rs.$750$

(b) Rs.$75$

(c) Rs.$625$

(d) Rs.$62.50$

Ans: Correct answer is (d).

Interest on Rs.$5000$ at the rate of $15\%$ per annum

Interest $=5000\times \dfrac{15}{100}$

$=750$

For annum interest $=750$

For months interest $=\dfrac{750}{12}$

= Rs.$62.50$

Example 4: If two ratios are equivalent, then the four quantities are said to be in _______.

Ans: If two ratios are equivalent, then the four quantities are said to be in proportion.

Proportion is an equation that defines that the two given ratios are equivalent to each other.

Example 5: $40\%$ of $250km$ is ________.

Ans: $40\%$ of $250km$ is $100km$.

$40\%$ of $250km=\dfrac{250 \times 40}{100}=100$

In Examples 6 and 7, state whether the statements are True or False.

Example 6: If $25\%$ of the journey is $800km$, the total distance of the journey is $3000km$.

Ans: Statement is false.

Let total distance $=x$

$25\%$ of $x$ is $800km$

$x\times \dfrac{25}{100}=800$
$x= 800 \times 4=3200km$

Example 7: $0.05$ is equivalent to $5\%$.

Ans: Statement is true.

$= 0.05 \times 100\%=5\%$

Example 8: Suhana sells a sofa set for Rs. $9600$ making a profit of $20\%$. What is the CP of the sofa?

Ans: Let CP of the sofa is Rs. $x$

Profit$=20\%$ of x = $\dfrac{20}{100}x = \dfrac{x}{5}$

Therefore, 

SP=$x+ \dfrac{x}{5}= \dfrac{6x}{5}$

$SP=\dfrac{6x}{5}=9600$

$x=8000$

CP of the sofa set is Rs.$8000$.

Example 9: John borrowed Rs.$75000$ from his friend and after one year returned $80000$ to his friend, find the interest?

Ans: Borrowed amount $=75000$

Returned amount $=80000$

Interest for one year =$80000-75000=5000$

Example 10: If Meenakshee pays an interest of Rs.$1500$ for $4$ years on a sum of $2500$. Find the rate of interest per annum (P.A)?

Ans: $P=Rs.2500,T=4yr,I=Rs.1500,R=?$

Now, $I=\dfrac{P\times R\times T}{100}$

Therefore, $1500=\dfrac{2500\times R\times 4}{100}$

$R=\dfrac{1500}{100}=15$

So, the rate of interest is $15\%$.

Example 11: Refer to the graphic. If a Cheetah and tortoise travel at their top speeds for $1\min$; how much farther does the cheetah travel?

Ans: Speed $=\dfrac{\text{distance}}{\text{time}}$

First, determine the distance travelled by each animal in $1\min $.

So here, $1,\min =60\sec $

Find the difference travelled by two animals.

Distance cheetah travels in $1\min $= $31.3\times 60=1878m$

distance tortoise travels in $1\min $=$0.08\times 60=4.8m$

So the difference $=1878m-4.8m$

$=1873.2m$

Exercise

In questions 1 to 23, there are four options, out of which one is correct. Write the correct one.

1. 20% of 700 m is

(a) 560 m

(b) 70 m

(c) 210 m

(d) 140 m

Ans: Option d is correct.

20% of $700 \mathrm{~m}$

The above condition can be written as $=$

$=\left(\dfrac{20}{100}\right) \times 700$

$=\dfrac{14000}{100}$

$=140 \mathrm{~m}$

2. Gayatri’s income is ₹1,60,000 per year. She pays 15% of this as house rent and 10% of the remainder on her child’s education. The money left with her is

(a) ₹136000

(b) ₹120000

(c) ₹122400

(d) ₹14000

Ans: Option c is correct.

Gayatri Income $=1,60,000$

find house rent-

$=\dfrac{15}{100} \times 160000=24,000$

$\text { Now Amount } =160000-24000$

$=Rs1,36,000$

Now Gaytri spend money for child -

$=10 \% \text { of } 1,36,000$ 

$=\dfrac{10}{100} \times 136000$

$=Rs. 13600$

$=136000-13600$

$=122,400$Rs

3. The ratio of Fatima’s income to her savings is 4:1. The percentage of money saved by her is:

(a) 20%

(b) 25%

(c) 40%

(d) 80%

Ans: Option b is correct.

Let assume the ratio if Fatima’s income to her saving be $4 y: y$ 

Then the percentage of money saved by her is

$=\left(\dfrac{\text { Her saving }}{\text { Income }}\right) \times 100$

$=\dfrac{y}{4 y} \times 100$

$=\dfrac{100}{4}$

$=25 \%$

4. 0.07 is equal to

(a) 70%

(b) 7%

(c) 0.7%

(d) 0.07%

Ans: Option b is correct.

Given $0.07$

We need to find out in percentage

$\therefore 0.07=\dfrac{7}{100}$

$\Rightarrow$ The percentage form of $\dfrac{7}{100} =\dfrac{7}{100} \times 100 \%$

$=7 \%$

5. In a scout camp, 40% of the scouts were from Gujarat State and 20% of these were from Ahmedabad. The percentage of scouts in the camp from Ahmedabad is:

(a) 25

(b) 32.5

(c) 8

(d) 50

Ans: (c) is correct option.

From the question it is given that.

In a scout camp 40% of the scouts were from Gujarat.

So, let us assume the number of scouts in the camp is 100.

Then scouts from Gujarat $=40 \%$ of 100

$=\dfrac{40}{100} \times 100$

=40

Now $20 \%$ of scout were from Ahmedabad

$=20 \% \text { of } 40$

$=\dfrac{20}{100} \times 40$

=8

Therefore the percentage of scout in the camp from Ahmedabad is $8 .$

6. What percent of ₹ 4500 is ₹9000?

(a) 200

(b) $\dfrac{1}{2}$

(c) 2

(d) 50

Ans: (a) is correct option. 

Let the percentage be $X \%$

\[\Rightarrow X\% \text{ of }4500=9000\]

\[\Rightarrow \dfrac{X}{100}\times 4500=9000\]

\[\Rightarrow 45X=9000\]

\[\Rightarrow X\%=\dfrac{9000}{45}\]

\[\Rightarrow X\%=200\]

7. $5.2$ is equal to

(a) $52 \%$

(b) $5.2 \%$

(c) $520 \%$

(d) $0.52 \%$

Ans: (c) is correct option. 

We can write 5.2 $=\dfrac{52}{10}$

$=\dfrac{52}{10}\times 100\%$

$=520\%$

8. The ratio $3: 8$ is equal to

(a) $3.75 \%$

(b) $37.5 \%$

(c) $0.375 \%$

(d) $267 \%$

Ans: (b) is correct option. 

Given,

$\text { Ratio }=3: 8$ 

We need to find out in percentage

$\therefore 3: 8=\dfrac{3}{8}$

The percentage form of $\dfrac{3}{8}$ can be written as $\dfrac{3}{8} \times 100\%$

$=37.5 \%$

9. $225 \%$ is equal to

(a) $9: 4$

(b) $4: 9$

(c) $3: 2$

(d) $2: 3$

Ans: (a) is the correct option. 

Given $225 \%$

Need to write it in ratio form

$\%$ can be removed by dividing the given number by 100

It can be write as $225 \times \dfrac{1}{100}$ 

$=\dfrac{225}{100}$

$=\dfrac{9}{4}$

$\therefore$ ratio $=9: 4$

10. A bicycle is purchased for ₹ 1800 and is sold at a profit of $12 \%$. Its selling price is

(a) ₹ 1584

(b) ₹ 2016

(c) ₹ 1788

(d) ₹ 1812

Ans: (b) is the correct option. 

Given,

Purchase price of bicycle $=1800$

And profit $=12\%$

As we know

$\text { Profit % }=\dfrac{\text { Profit }}{C P} \times 100$

$12=\dfrac{\text { Profit }}{1800} \times 100$

$\text { Profit }=12 \times 18=216$

$\therefore S P=C P+\text { Profit }$

$\therefore S P=1800+216$

$SP=2016$

11. A cricket bat was purchased for ₹ 800 and was sold for ₹ 1600 . Then profit earned is

(a) $100 \%$

(b) $64 \%$

(c) $50 \%$

(d) $60 \%$

Ans: (a) is correct option. 

Given,

Cost price of Bot $=800 Rs$

Selling price of Bot $=1600 \mathrm{Rs}$

Profit $=1600-800=800$

Now,

$\text { Profit % }=\dfrac{\text { Profit }}{\text { Cost price }} \times 100$

$\text { Profit % }=\dfrac{800}{800} \times 100$

$\text { Profit % }=100 \%$

12. A farmer bought a buffalo for ₹ 44000 and a cow for ₹ 18000 . He sold the buffalo at a loss of $5 \%$ but made a profit of $10 \%$ on the cow. The net result of the transaction is

(a) loss of ₹ 200

(b) profit of $₹ 400$

(c) loss of ₹ 400

(d) profit of ₹ 200

Ans: (c) is correct option. 

For Buffalo $\mathrm{CP}=44000 \mathrm{Rs}$

$\text { Loss% }=5 \%$

$\therefore \text { Loss% }=\dfrac{\text { Loss }}{\text { CP }} \times 100 \%$

$\Rightarrow 5=\dfrac{\text { Loss }}{44000} \times 100$

$\Rightarrow \text { Loss }=5 \times 440=2200$

So,

$\mathrm{SP}=\mathrm{CP}-\text { Loss }$

$\mathrm{SP}=44000-2200$

$\mathrm{SP}=41800 \mathrm{Rs}$

$\rightarrow \text { For cow } \mathrm{CP}=18000$

$\text { Profit % }=10 \%$

$\therefore \text { Profit % }=\dfrac{\text { Profit }}{\text { CP }} \times 100 \%$

$\Rightarrow 10=\dfrac{\text { Profit }}{18000} \times 100$

$\Rightarrow \text { Profit }=1800 \text { Rs }$

So

$\mathrm{SP}=\mathrm{CP}+\text { profit }$

$\mathrm{SP}=18000+1800$

$\mathrm{SP}=19800 \mathrm{Rs}$

Total CP of Buffalo and cow

$=44000+18000$

$=62000$

Total SP of Buffalo and cow

$=41800+19800$ $=61600$ 

Net loss $=$ CP $-$ SP 

Net loss $=62000-61600$

Net loss $=400 R s$

13. If Mohan's income is $25\%$ more than Raman's income, then Raman's income is less than Mohan's income by

(a) $25 \%$

(b) $80 \%$

(c) $20 \%$

(d) $75 \%$

Ans: (c) is correct option. 

Let the raman income be $x$ it is given that Mohan's income is $25 \%$ more than Raman's income.

Then, Mohan income = $x+25 \%$ of x

$=x+\dfrac{25x}{100}$

$=x\left(1+\dfrac{25}{100}\right)$

$=x\left(\dfrac{100+25}{100}\right)$

$=\dfrac{125}{100} x$ 

$\therefore$ Raman's income as compared to Mohan's income $=\dfrac{\text { Mohan's income- Raman's income }}{\text { Mohan's income }} \times 100 \%$ 

$=\dfrac{\dfrac{125 x}{100}-x}{\dfrac{125 x}{100}} \times 100 \%$ 

$=\dfrac{25 x}{125 x} \times 100 \%$ 

$=20 \%$ 

14. The interest on ₹ 30000 for 3 years at the rate of $15 \%$ per annum is

(a) ₹ 4500

(b) ₹ 9000

(c) ₹ 18000

(d) ₹ 13500

Ans: (d) is correct option. 

Given,

$\text { Principal }=30000$

$\text { Time }=3 \text { year }$

$\text { Rate }=15 \% \text { P. }a$ 

Now for formula of Interest

$\text { Interest} =\dfrac{\text{ Principal } \times \text{ Rate } \times \text {Time }}{100}$

$\text { Interest} =\dfrac{30000 \times 15 \times 3}{100}$

$\text { Interest}=13,500$

15. Amount received on ₹ 3000 for 2 years at the rate of $11 \%$ per annum is

(a) ₹ 2340

(b) ₹ 3660

(c) ₹ 4320

(d) ₹3330

Ans: (b) is correct option. 

Given,

$\text { Principle }=3000$

$\text { Time }=2 \text { year }$

$\text { Rate }=11 \%$

Now first of all Calculate Interest

$\text { Interest }=\dfrac{\text { Principle } \times \text { Rate } \times \text { Time }}{100}$

$\text { Interest }=\dfrac{3000 \times 11 \times 2}{100}$

$\text { Interest }=\mathrm{Rs}660 $

$\text { Amount }=\mathrm{P}+\mathrm{I}$

$\text { Amount }=3000+660$

$\text { Amount }=\mathrm{Rs}3660 $

16. Interest on ₹ 12000 for 1 month at the rate of $10 \%$ per annum is

(a) ₹ 1200

(b) ₹ 600

(c) ₹ 100

(d) ₹ 12100

Ans: (c) is correct option. 

$\text { Principal }=12000 \mathrm{Rs}$

$\text { Time }=1 \text { month }=\dfrac{1}{12} \text { year }$

 $\text { Rate }=10 \%$

$\text { Simple Interest }=\dfrac{\text { Principal } \times \text { Time } \times \text { Rate }}{100}$

$\text { Simple Interest }=\dfrac{12000 \times 1 \times 10}{12 \times 100}$

$\text { Simple Interest }=100 \mathrm{Rs}$

17. Rajni and Mohini deposited ₹3000 and ₹ 4000 in a company at the rate of $10 \%$ per annum for 3 years and $2 \dfrac{1}{2}$ years respectively. The difference of the amounts received by them will be

(a) ₹ 100

(b) ₹ 1000

(c) ₹ 900

(d) ₹ 1100

Ans: (d) is correct option. 

For Rajni,

Principal $=3000$ Time $=3$ years Rate $=10 \% P . a .$ 

Simple Interest $=\dfrac{\text { Principal } \times \text { Time } \times \text { Rate }}{100}$

Simple Interest $=\dfrac{3000 \times 3 \times 10}{100}$

Simple Interest $=900 R s$

Now,

Amount = Principal + Simple Interest

Amount $=3000+900$

Amount $=3900 R s$

Now, for Mohini

Principal $=4000 R s$

Time $=2 \dfrac{1}{2}$ years $=\dfrac{5}{2}$ years Rate $=10 \%P$.$a.$ 

Simple Interest $=\dfrac{\text { Principal } \times \text { Time } \times \text { Rate }}{100}$

Simple Interest $=\dfrac{4000 \times 5 \times 10}{2 \times 100}$

Simple Interest $=1000 Rs$

Amount = Principal $+$ Simple Interest

Amount $=4000+1000$

Amount $=5000 Rs$

Now, Difference in the amounts of Rajini and Mohini $=5000-3900=1100 Rs$

18. If $90 \%$ of $x$ is $315 \mathrm{~km}$, then the value of $x$ is

(a) $325 \mathrm{~km}$

(b) $350 \mathrm{~km}$

(c) $405 \mathrm{~km}$

(d) $340 \mathrm{~km}$

Ans: (b) is correct option. 

Given,

$90 \% \text { of } x=315 \mathrm{~km}$

$\Rightarrow \dfrac{90}{100} \times x=315$

$\Rightarrow 90 x=315 \times 100$

$\Rightarrow x=\dfrac{315 \times 100}{90}$

$\Rightarrow x=350 \mathrm{~km}$

19. On selling an article for ₹329, a dealer lost 6%. The cost price of the article is

(a) ₹310.37

(b) ₹348.74

(c) ₹335

(d) ₹350

Ans: (d) is correct option. 

Given,

Selling Price $=329 R s$

$\operatorname{Loss}=6 \%$

Cost Price $=$ ?

Cost Price $=\dfrac{\text { Selling Price } \times 100}{(100-\text { Loss } \%)}$

Cost Price $=\dfrac{329 \times 100}{100-6}$

Cost Price $=350 Rs$

20. $\dfrac{\text{(25% of 50% of 100%)}}{25 \times 50}$ is equal to

(a) $1.1 \%$

(b) $0.1 \%$

(c) $0.01 \%$

(d) $1 \%$

Ans: (c) is correct option. 

$=\dfrac{25 \% \text { of } 50 \% \text { of } 100 \%}{25 \times 50}$

$=\dfrac{\dfrac{25}{100} \times \dfrac{50}{100} \times \dfrac{100}{100}}{25 \times 50}$

$=\dfrac{1}{10,000}$

$=\dfrac{0.01}{100}$

$=0.01 \%$

21. The sum which will earn a simple interest of ₹ 126 in 2 years at $14 \%$ per annum is

(a) ₹394

(b) ₹ 395

(c) ₹450

(d) ₹540

Ans: (c) is correct option. 

Given,

Simple Interest $=126 R s$

$\text { Time }=2 \text { years }$

$\text { Rate }=14 \% \text { p.a. }$

Now,

$\text { Simple Interest }=\dfrac{\text { Principal } \times \text { Rate } \times \text { Time

}}{100}$

$\Rightarrow 126=\dfrac{\text { Principal } \times 14 \times 2}{100}$

$\Rightarrow \text { Principal }=\dfrac{126 \times 100}{14 \times 2}$

$\Rightarrow \text { Principal }=450 \mathrm{Rs}$

22. The percent that represents the unshaded region in the figure.

(a) $75 \%$ 

(b) $50 \%$ 

(c) $40 \%$ 

(d) $60 \%$

Ans: (c) is correct option. 

As shown in figure, we have

Shaded parts $=60$

Unshaded parts $=40$

Total parts $=100$

Therefore Unshaded region $=\dfrac{40}{100}$

$=40 \%$

23. The percent that represents the shaded region in the figure is

(a) $36 \%$ 

(b) $64 \%$ 

(c) $27 \%$ 

(d) $48 \%$

Ans: (a) is correct option. 

As shown in figure, we have

Unshaded parts $=64$

Shaded parts $=36$

Total parts $=100$

$\therefore$ Therefore Shaded region $=\dfrac{36}{100}$

$=36 \%$

Direction: In each of the questions 24 to 59 , fill in the blanks to make the statements true.

24. 2:3 =_________%

Ans: $2: 3 = 66\%$

$2: 3=\dfrac{2}{3}$

We divide 2 by 3 , We get

$=0.66$

$=\dfrac{66}{100}$

$=66 \%$

25. $18\dfrac{3}{4}\%=$___________$:$__________.

Ans: $18\dfrac{3}{4} \%=3: 16$

We have $18\dfrac{3}{4} \%$

We can write it as $\dfrac{75}{4} \%$

$=\dfrac{75}{4} \times \dfrac{1}{100}$

$=\dfrac{3}{16}$

$=3: 16$

26. $30 \%$ of $₹ 360=$___________

Ans: $30 \% \text { of } ₹ 360 =₹ 108$

$30 \% \text { of } ₹ 360$

$\Rightarrow =\dfrac{30}{100} \times 360$

$\Rightarrow =3 \times 36$

$\Rightarrow =₹ 108$

27. $120 \%$ of $50 \mathrm{~km}=$___________

Ans: $120 \%$ of $50 \mathrm{~km}=60 \mathrm{~km}$

$120 \%$ of $50 \mathrm{~km}$

$\Rightarrow =\dfrac{120}{100} \times 50$

$\Rightarrow =12 \times 5$

$\Rightarrow =60 \mathrm{~km}$

28. $2.5=$ ________%

Ans: 2.5=250%

We can write $2.5$ as

$=\dfrac{25}{10} \times \dfrac{10}{10}$

$=\dfrac{250}{100}$

$=250 \%$

29. $\dfrac{8}{5}=$____________%

Ans: $\dfrac{8}{5}= 160 \%$

$\Rightarrow \dfrac{8}{5}=1.6$

We can write $1.6$ as

$=\dfrac{16}{10} \times \dfrac{10}{10}$

$=\dfrac{160}{100}$

$=160 \%$

30. A__________ with its denominator 100 is called a percent.

Ans: Fraction.

A fraction with its denominator 100 is known as a percent.

31. 15 Kg is __________% of 50 kg.

Ans: $15 \mathrm{~kg}$ is $30 \%$ of $50 \mathrm{~kg}$

Suppose, $y\%$ of $50 \mathrm{~kg}$ is $15 \mathrm{~kg}$

$y \% \times 50=15$

$\Rightarrow \dfrac{y}{100} \times 50=15$

$\Rightarrow y=\dfrac{15 \times 100}{50}$

$\Rightarrow y=15 \times 2$

$\Rightarrow y=30 $

32. Weight of Nikhil increased from $60 \mathrm{~kg}$ to $66 \mathrm{~kg}$. Then, the increase in weight is ____$\%$

Ans: Weight of Nikhil increased from $60 \mathrm{~kg}$ to $66 \mathrm{~kg}$. Then, the increase in weight is $10 \%$

Explanation:

Given,

Previous weight of Nikhil $=60 \mathrm{~kg}$

Present weight $=66 \mathrm{~kg}$

Nikhil weight increased by $=66-60=6 \mathrm{~kg}$

So, Increase $\%$ of weight is ratio of the increased weight by previous weight

$\therefore \text { increase } \%=\dfrac{6}{60}\times 100 \%$

$\Rightarrow \dfrac{6}{60} \times 100=10 \%$

33. In a class of 50 students, $8 \%$ were absent on one day. The number of students present on that day was_________

Ans: In a class of 50 students, $8 \%$ were absent on one day. The number of students present on that day was 46.

Explanation:

Given,

Number of students in the class $=50$

Percentage of students absent $=8 \%$

Let, find out number of students absent on that day $=8 \%$ of 50

$\Rightarrow \dfrac{8}{100} \times 50=4$

So, number of students absent is 4

Hence, total number of students present on that day $=50-4=46$

34. Savitri obtained 440 marks out of 500 in an examination. She secured ________ $\%$ marks in the examination.

Ans: Savitri obtained 440 marks out of 500 in an examination. She secured $88 \%$ marks in the examination.

Explanation:

Given,

Total marks in examination $=500$

Savitri obtained marks out of total $=440$

Therefore, let's find out percentage of marks she scored

$\dfrac{440}{500} \times 100=88 \%$

Hence, she obtained $88 \%$ of marks in the examination.

35. Out of a total deposit of ₹ 1500 in her bank account, Abida withdrew $40 \%$ of the deposit. Now the balance in her account is___________

Ans: Out of a total deposit of $₹ 1500$ in her bank account, Abida withdrew $40 \%$ of the deposit. Now the balance in her account is ₹ $900$.

Explanation:

Given,

Total deposit of amount in the bank $=₹ 1500$

Percentage of amount withdrawn by Abida $=40 \%$

Let's find out the amount of money withdrawn

$\Rightarrow \dfrac{40}{100} \times 1500= ₹ 600$

Hence, her balance amount will be $1500-600=₹ 900$

36. _______ is $50 \%$ more than 60.

Ans: 90 is $50 \%$ more than 60.

Explanation:

Let's suppose y be the $50 \%$ more than 60 .

$\therefore y=\dfrac{50}{100} \times 60+60$

$\Rightarrow y=30+60$

$\Rightarrow y=90$

Hence, 90 is $50 \%$ more than 60.

37. John sells a bat for $₹ 75$ and suffers a loss of $₹ 8$. The cost price of the bat is__________

Ans: Given,

The selling price for Bat = ₹75

Loss he suffers $=₹ 8$

Let's find the cost price for the Bat

Cost price $=$ selling price $+$ loss

$\Rightarrow 75+8=83$

Hence, the cost price for the Bat is ₹83

38. If the price of sugar is decreased by $20 \%$, then the new price of $3 \mathrm{~kg}$ sugar originally costing ₹120 will be__________

Ans: Given,

Original price for the $3 \mathrm{~kg}$ sugar $=₹ 120$

Let find the price of $1 \mathrm{~kg}$ sugar

$\Rightarrow \dfrac{120}{3}=R s 40$

Given, Price of sugar decreased by the $20 \%$

Then, The decreased amount $=\dfrac{20}{100} \times 40=R s 8$

Hence, the new price for the $1 \mathrm{~kg}$ sugar is $40-8=₹ 32$

The price of $3 \mathrm{~kg}$ sugar $=32 \times 3=Rs 96$

39. Mohini bought a cow for ₹ 9000 and sold it at a loss of ₹ 900 . The selling price of the cow is_________

Ans: Mohini bought a cow for $₹ 9000$ and sold it at a loss of ₹900. The selling price of the cow is $₹ 8100$

Explanation

Given,

Cost price of the cow brought by Mohini = ₹9000

The loss = ₹900

Let's find out the selling price of the cow

Selling price $=$ Cost price - Loss

$\Rightarrow 9000-900=8100$

Hence, the selling price for the cow is ₹8100

40. Devangi buys a chair for ₹ 700 and sells it for ₹750. She earns a profit of ________$\%$ in the transaction.

Ans: Devangi buys a chair for ₹700 and sells it for ₹750 in the transaction. 

Explanation: 

Given, Cost price of the chair brought by Devangj = ₹700

Selling price of the chair $=₹ 750$

Let's find out the profit she earns

Profit = selling price - cost price

$\Rightarrow 750-700=50$

Therefore, profit percentage

$=\dfrac{50}{700} \times 100\%$

$=\dfrac{50}{7}\%$

$=7 \dfrac{1}{7}\%$

41. Sonal bought a bed sheet for ₹ 400 and sold it for ₹ 440 . Her _______$\%$ is______

Ans: Sonal bought a bed sheet for $₹ 400$ and sold it for $₹ 440$. Her $10 \%$ is profit.

Explanation:

Given,

Cost price for the Bedsheet bought by Sonal $=₹ 400$

Selling price for the Bedsheet sold it $=₹ 440$

By the given values selling price is more the cost price

S.P $>$ C.P

So, it's clearly a Profit

Therefore,

profit = selling price $-$ cost price

$\Rightarrow 440-400=Rs 40$

$\therefore$ Profit $\%$ will be

$=\dfrac{40}{400} \times 100$

$=10 \%$

Hence, she having profit of $10 \%$

42. Nasim bought a pen for $₹ 60$ and sold it for ₹54. His ________$\%$ is___________

Ans: Nasim bought a pen for $₹ 60$ and sold it for ₹54. His $10 \%$ is loss.

Explanation:

Given,

Cost price of the pen $=₹ 60$

Selling price of the pen $=₹ 54$

By the given value cost price is more than selling price

C.P $>S . P$

Hence, it's a loss on selling the pen.

Therefore,

Loss = Cost price - Selling price

$\Rightarrow 60-54=Rs 6$

Therefore, calculation of loss %

$\therefore$ loss $\% = \dfrac{6}{60} \times 100$

$=10 \%$

Hence, He having loss of $10 \%$

43. Aahuti purchased a house for $₹ 50,59,700$ and spent $₹ 40300$ on its repairs. To make a profit of $5 \%$, she should sell the house for ₹__________

Ans: Aahuti purchased a house for ₹50, 59,700 and spent ₹40300 on its repairs. To make a profit of $5 \%$, she should sell the house for $₹ 5355000$.

Explanation:

Given,

Cost price of purchasing amount of house $=₹ 50,59,700$

Amount spent on repairing the house $=₹ 40,300$

Hence, total cost price of the house $=5059700+40300=5100000$

Given,

The profit percentage is $5 \%$

Let's find out the what will be selling price

$S . P=\left(\dfrac{100+\operatorname{Pr} o f i t \%}{100}\right) \times C . P$

$\therefore S . P=\left(\dfrac{100+5}{100}\right) \times 5100000$

$\Rightarrow S . P=105 \times 51000$

$\Rightarrow S . P=R s 5355000$

Hence, Selling price will be ₹5355000 if Aahuti wants $5 \%$ profit from the house.

44. If 20 lemons are bought for $₹ 10$ and sold at 5 for three rupees, then_______ in the transaction is___________$\%$

Ans: If 20 lemons are bought for $₹ 10$ and sold at 5 for three rupees, then profit in the transaction is $20 \%$.

Explanation:

Given,

Cost price of the 20 lemons is brought $=₹ 10$

So, the price of 1 lemon $\Rightarrow \dfrac{10}{20}=Rs \dfrac{1}{2}$

Given, the selling price of 5 lemons $=₹ 3$

Selling price of 1 lemon $=\dfrac{3}{5}$

It's clearly selling price is more than cost price

Here, S.P > C.P

$=\dfrac{3}{5}-\dfrac{1}{2}$

$=\dfrac{6-5}{10}$

$=\dfrac{1}{10}$

Now, Profit percentage will be

$\text { profit % } =\dfrac{\dfrac{1}{10}}{\dfrac{1}{2}} \times 100$

$=\dfrac{1}{10} \times \dfrac{2}{1} \times 100$

$=20 \%$

Hence, he earns $20 \%$ profit.

45. Narain bought 120 oranges at $₹ 4$ each. He sold $60 \%$ of the oranges at ₹5 each and the remaining at ₹ $3.50$ each. His ________is________$\%$

Ans: Narain bought 120 oranges at ₹ 4 each. He sold $60 \%$ of the oranges at ₹5 each and the remaining at $₹ 3.50$ each. His profit is $10 \%$.

Explanation:

Given, total number of oranges bought by the Narain $=120$

$60 \%$ of total orange will be

$=\dfrac{60}{100} \times 120$ $=72$ 

Number of oranges remaining $\Rightarrow 120-72=48$ 

Now, The buying price of 120 oranges $=120 \times 4=R s 480$ 

The selling price of 72 oranges $=72 \times 5=R s 360$ 

The selling price of 48 oranges $=48 \times 3.50=R s 168$ 

The selling price of 120 oranges $=360+168=R s 528$ 

Here, the selling price is more than the cost price S.P.> C.P 

Therefore, profit earn by Narain $\Rightarrow 528-480=R s 48$ 

profit % $=\dfrac{48}{480} \times 100$ $=10 \%$ 

Hence, He get profit by $10 \%$

46. A fruit seller purchased $20 \mathrm{~kg}$ of apples at $₹ 50$ per $\mathrm{kg}$. Out of these, $5 \%$ of the apples were found to be rotten. If he sells the remaining apples at ₹ 60 per kg, then his _______is ______$\%$.

Ans: A fruit seller purchased $20 \mathrm{~kg}$ of apples at $50 \mathrm{Rs}$ per $\mathrm{kg}$. out of these, $5 \%$ of the apple were found to be rotten. If he sells the remaining apples at 62 per $\mathrm{kg}$ then his profit is $14 \%$.

Given,

Total purchased apple $=20 \mathrm{~kg}$

Total apples were found rotten $=5 \%$ purchased

$=\dfrac{5}{100} \times 20=1 \mathrm{~kg}$ apple

remaining apple $=20-1=19 \mathrm{~kg}$

Cost price of $20 \mathrm{~kg}$ apples $=20 \times 50=1000 \mathrm{Rs}$

Selling price of $19 \mathrm{~kg}$ apples $=19 \times 60=1140 \mathrm{Rs}$

Now,

$\Rightarrow$ Selling price $-$ Cost price $\Rightarrow 1140-1000=140 R s$ 

Profit % $=\dfrac{\text { Profit }}{\text { Cost price }} \times 100$ 

Profit % $=\dfrac{140}{1000} \times 100$

Profit % $=14 \%$

47. Interest on ₹ 3000 at $10 \%$ per annum for a period of 3 years is_____

Ans:

Interest on $3000 R s$ at $10 \%$ per annum for a period of 3 years is $R s 900$

Given,

Principal = 3000 Rs

Time = 3years

Rate $=10 \%$

$\text { Interest }=\dfrac{\text { Principal } \times \text { Time } \times \text { Rate }}{100}$ 

$\text { Interest }=\dfrac{3000 \times 3 \times 10}{100}$ 

$\text { Interest } = \mathrm{Rs} 900$

Interest on $R s 3000$ at $10 \%$ for 3 years is 900

48. Amount obtained by depositing $₹ 20,000$ at $8 \%$ per annum for six months is___________.

Ans: Given,

Principal $=20,000$

Time $=6$ months $=\dfrac{1}{2}$ years

Rate $=8 \%$ per annum

Interest $=\dfrac{\text { Principal } \times \text { Time } \times \text { Rate }}{100}$ 

Interest $=\dfrac{20000 \times 8 \times 1}{100 \times 2}$ 

Interest $=Rs 800 $ 

Total Obtained amount $=$Principal $+$Interest $=20000+800$

$=Rs.20800$

49. Interest on ₹ 12500 at $18 \%$ per annum for a period of 2 years and 4 months is______

Ans: Interest on $R s 12500$ at $18 \%$ per annum for a period of $2$ years and 4 month is 5250 .

Given,

$\text { Principal }=R s 12500$

$\text { Rate }=18 \% p . a$

Time $=2$ years and 4 month

Total Time $=\dfrac{28}{12}=\dfrac{7}{3}$ years

$\text { Interest }=\dfrac{\text { Principal } \times \text { Rate } \times \text { Time }}{100}$

$\text { Interest }=\dfrac{12500 \times 18 \times 7}{100 \times 3}$

$\text { Interest }=Rs 5250$

Interest on Rs1 2500 at $18 \%$ for $2 $ years and 4 month is Rs5250.

50.  25 $\mathrm{ml}$ is _________percent of 5 litres.

Ans: $25 ml$ is $0.5$ percent of 5 litres.

Given,

Total liter count $=5$ litres.

Let $25 ml$ be the $x \%$ of the 5 litres

$\therefore \dfrac{x}{100} \times 5=\dfrac{25}{1000} \text { litres }$

$x=\dfrac{25}{1000} \times \dfrac{100}{5}$

$x=\dfrac{5}{10}$

$x=0.5 \%$

Now $0.5 \%$ is the total percentage for $25 \mathrm{ml}$ ot 5 litres.

51. If $A$ is increased by $20 \%$, it equals $B .$ If $B$ is decreased by $50 \%$, it equals $C .$ Then __________$\%$ of $\mathrm{A}$ is equal to $\mathrm{C}$.

Ans: If $A$ is increased by $20 \%$, It equals $B$. If $B$ is decreased by $50 \%$. It equals $C$, Then $60 \%$ of $A$ is equal to $C$.

Given,

$A$ increased by $20 \%=A+\dfrac{20}{100} \times A$

$B$ increased by $50 \%=B-\dfrac{50}{100} \times B$

$A+\dfrac{20}{100} \times A=B \ldots \ldots \ldots \ldots . .(1)$

$B-\dfrac{50}{100} \times B=C \ldots \ldots \ldots \ldots . .(2)$

$\Rightarrow A\left(1+\dfrac{1}{5}\right)=B$ and $B\left(1-\dfrac{1}{2}\right)=C$

$(\because$ To put $A$ and $B$ common from eq $(1)$ and eq $(2))$

$\dfrac{6}{5} A=B$ and $\dfrac{1}{2} B=C$

$\dfrac{6}{5} A=B$ and $B=2 C$ (By solving)

Now,

$B=2 C$

$\dfrac{6}{5} A=B$

$\therefore \dfrac{6}{5} A=2 C$

$\Rightarrow C=\dfrac{6}{10} A$

$\Rightarrow C=\dfrac{6}{10} \times \dfrac{10}{10} \times A$

$\Rightarrow C=60 \%$ of $A$

Now, $60 \%$ of $A$ is equal to $C$

52. Interest $=\dfrac{P \times R \times T}{100}$, where $\mathrm{T}$ is_________ $\mathrm{R} \%$ is________ and $\mathrm{P}$ is________

Ans: Interest $=\dfrac{P \times R \times T}{100}$, where

T is time period

$R$ is Rate of Interest

$P$ is Principal

We can find Interest by multiplying the Principal,Rate of Interest and Time period and divide all of them by 100.

53. The difference of interest for 2 years and 3 years on a sum of $₹ 2100$ at $8 \%$ per annum is______

Ans: The difference of interest for 2 years and 3 years on a sum of Rs 2100 at $8 \%$ per annum is Rs 168 .

Given,

Principal = Rs 2100

Rate $=8 \%$ p.a.

To find out:-

difference of interest for 2 years and 3 years at $8 \%$ p.a.

Explanation:

Interest for 2 years $=\dfrac{2100 \times 8 \times 2}{100} \quad\left(\because I=\dfrac{P \times R \times T}{100}\right)$

Interest for 2 years $=$ Rs 336

Interest for 3 years $=\dfrac{2100 \times 8 \times 3}{100}$

Interest for 3 years $=$ Rs 504

difference $=504-336$

difference $=$ Rs 168

54. To convert a fraction into a percent, we _________it by 100 .

Ans: To convert a fraction into percent, we Multiply it by 100

Let $x$ be the fraction

Now, find out the fraction $(x)$ into a percent:-

$x \%=x \times 100$

(where $x$ is fraction)

55. To convert a decimal into a percent, we shift the decimal point two places to the_____

Ans: To convert a decimal into a percent, We shift the decimal point two places to the Right.

To find out the percent of any number it multiplies by 100 and when we multiply a number by 100 , the decimal point always shifts two places to the Right.

56. The __________of interest on a sum of $₹ 2000$ at the rate of $6 \%$ per annum for $1\dfrac{1}{2}$ years and 2 years is $₹ 420$.

Ans: The Sum of Interest on a sum of Rs 2000 at the Rate of $6 \%$ per annum for $1 \dfrac{1}{2}$ yeras and 2 years is Rs 420 .

Given,

Principal = Rs 2000

Rate $=6 \%$ p.a.

To find out:-

Total Interest for given time

Interest for $1 \dfrac{1}{2}$ years $=\dfrac{2000 \times 6 \times 3}{100}$

Interest $=$ Rs 180

Interest for 2 years $=\dfrac{2000 \times 6 \times 2}{100}$

Total Interest $=180+240$

The total Interest for given time is Rs 420 .

57. When converted into percentage, the value of $6.5$ is _________than $100 \%$

Ans: When converted into percentage the value of $6.5$ is more than $100 \%$

Given,

The Number $=6.5$

To find out:-

Which Number value is large

Explanation:

The percent of $6.5$ is

$=6.5 \times 100\%$

(To find percent multiply by 100 )

Now $650\% >100 \%$

The Number value $6.5$ percent is more than 100 percent.

In questions 58 and 59, copy each number line. Fill in the blanks so that each mark on the number line is labelled with a percent, a fraction and a decimal. Write all fractions in lowest terms.

58.

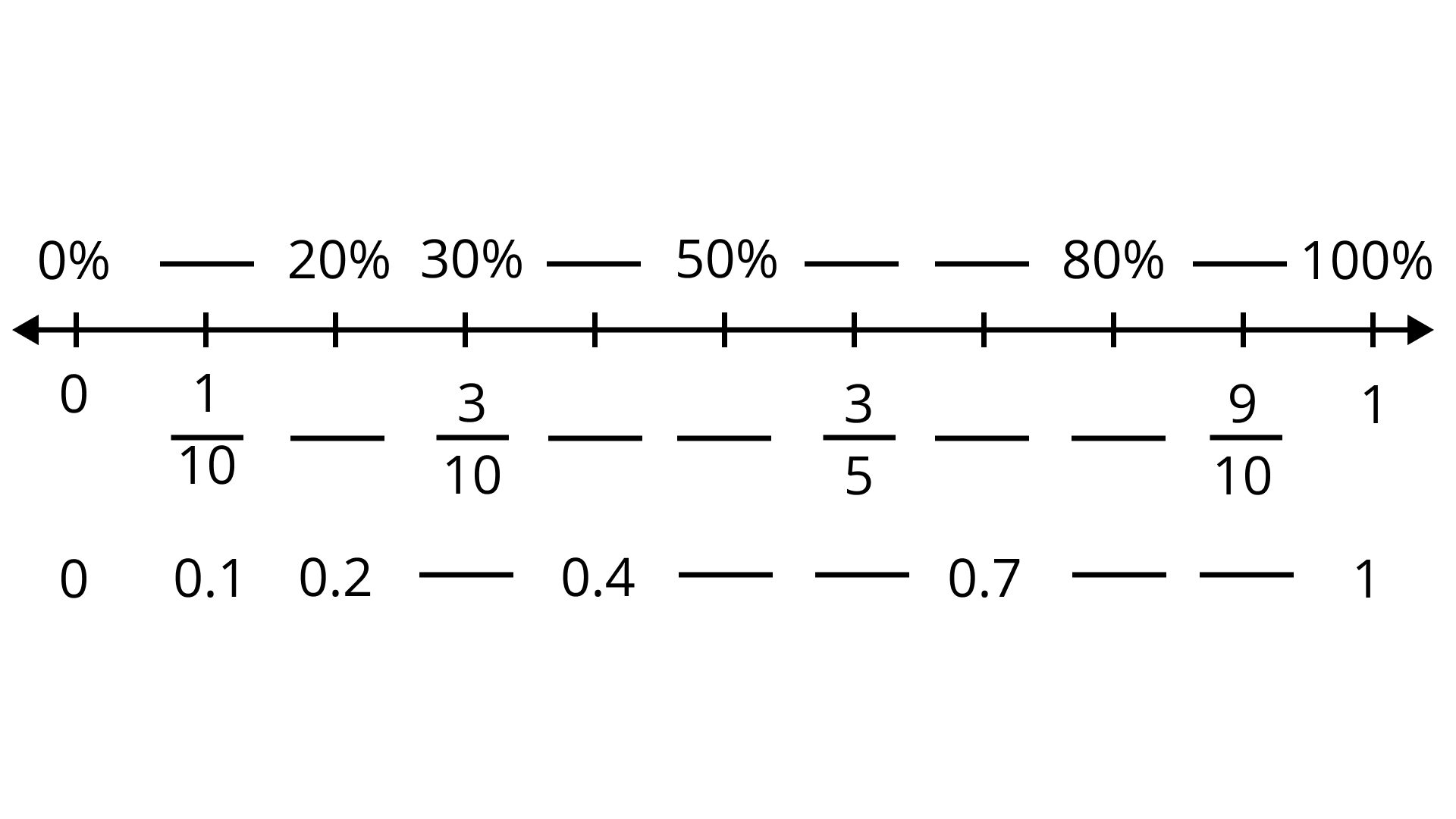
Ans:

For fraction $\dfrac{1}{10}$ and decimal $0.1$, the percent is $10\%$.

For percent $20\%$ and decimal $0.2$, the fraction is $\dfrac{2}{10}$.

For $30\%$ and $\dfrac{3}{10}$ fraction, the decimal is $0.3$.

For \[0.4\] decimal, the fraction is $\dfrac{4}{10}$ and percent is \[40\%\]

For \[50\%\], the fraction is \[\dfrac{1}{2}\] and the decimal is \[0.5\].

For \[\dfrac{3}{5}\] fraction, the percent is \[60\%\] and decimal is \[0.6\].

For \[0.7\] decimal, the percent is \[70\%\] and fraction \[\dfrac{7}{10}\]

For \[80\%\] the fraction is \[4/5\] and decimal is \[0.8\]

For \[\dfrac{9}{10}\] fraction, the percent is \[90\%\] and decimal is \[0.9\]

59.

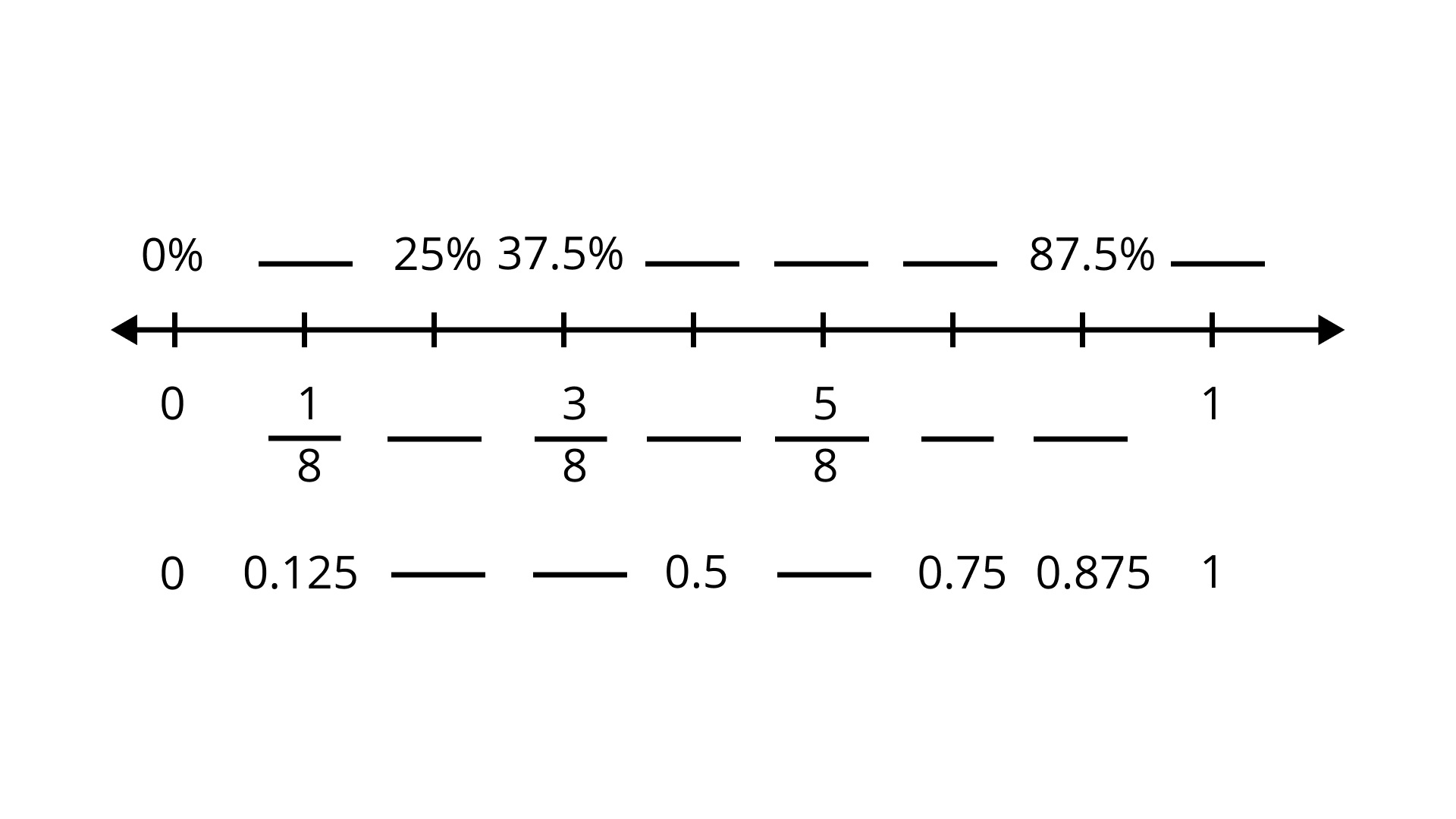
Ans

To find out:

The percent, fraction and decimal on the number line:

For $\dfrac{1}{8}$ fraction, the percent is $12.5\%$ and decimal is $0.125$

For $25\%$ the fraction is $\dfrac{1}{4}$ and decimal is $0.25$

For $37.5\%$ the fraction is $\dfrac{3}{8}$ and decimal is $0.375$

For $50\%$ the fraction is $\dfrac{1}{2}$ and decimal is $0.5$

For the fraction $\dfrac{5}{8}$, the percent is $62.5\%$ and decimal is $0.625$

For the decimal $0.75$, the percent is $75\%$ and fraction is $\dfrac{3}{4}$

For $87.5\%$, the fraction is $\dfrac{7}{8}$ and decimal is $0.875$

For $1$, the percent is $100\%$ 

In questions 60 to 79, state whether the statements are True or False.

60. $\dfrac{2}{3}=66\dfrac{2}{3}\%$

Ans: Given statement is true

By changing the fraction into percent.

$\dfrac{2}{3} = \dfrac{2}{3}\times 100\%$

$=\dfrac{200}{3}\%$

$=66\dfrac{2}{3}\%$ 

61. When an improper fraction is converted into percentage then the answer can also be less than $100$.

Ans: Its a False statement.

When an improper fraction is converted into percentage then the value is always greater than$100$. 

62. 8 hours is 50% of 4 days.

Ans: Its a False statement.

Hours in $1$day$=24$hours

Hence, hours in $4$days $=24\times 4=96$hours

Now, 

$50\%$of $96$hours

$\Rightarrow \dfrac{50}{100}\times 96=48$hours 

63. The interest on ₹350 at 5% per annum for 73 days is ₹35.

Ans: It's a False statement.

Principal$=Rs.350$

Rate $=5\%$p.a.

time$=73$days$=\dfrac{73}{365}$years

$\Rightarrow $interest $=\dfrac{350\times 5\times 73}{100\times 365}$

$\Rightarrow $interest $=\dfrac{2555}{2\times 365}=\dfrac{7}{2}$

Interest $=Rs.3.5$ 

64. The simple interest on a sum of ₹P for T years at R% per annum is given by the formula: Simple Interest $=\dfrac{T\times P\times R}{100}$

Ans: It is a true statement.

Because formula of interest $=\dfrac{T\times P\times R}{100}$

Where 

T=Time period

$R\%=$Rate of interest 

P=principal

65. 75% = $\dfrac{4}{3}$.

Ans: It's a False statement.

$75\%=\dfrac{75}{100}$

$\Rightarrow 75\%=\dfrac{3}{4}$ 

66. 12% of 120 are 100.

Ans: It's a False statement.

Because $12\%$ of $120$

$\Rightarrow \dfrac{12}{100}\times 120$

$\Rightarrow 14.40$

67. If Ankita obtains 336 marks out of 600, then the percentage of marks obtained by her is 33.6.

Ans: It's a False statement.

Total marks$=600$

The marks obtained by Ankita $=336$

Hence, the percentage of her marks 

$=\dfrac{336}{600}\times 100$

$=56\%$ 

68. 0.018 is equivalent to 8%.

Ans: Its a False statement.

$=0.018$

$=\dfrac{18}{1000}\times 100$

$=1.8\%$

69. 50% of ₹50 is ₹25.

Ans: Its a True statement.

$50\%$ of $50$

$=\dfrac{50}{100}\times 50$

$=Rs25$

70. 250 cm is 4% of 1 km.

Ans: It's a False statement.

$1km=1000m$

$1000m=1000\times 100cm\left\{ \therefore 1m=100cm \right\}$

$1000m=100000cm$

$=4\%$ of $1km=\left( \dfrac{4}{100}\times 100000 \right)cm$

$=4\%$ of $1km=4000cm$

71. Out of 600 students of a school, 126 go for a picnic. The percentage of students that did not go for the picnic is 75.

Ans: It's a False statement.

Number of students $=600$

Number of students went on a picnic $=126$

Hence,

Number of students who did not go for the picnic

$=600-126$

$=474$

Then the percentage of students who did not go for the picnic.

$=\dfrac{474}{600}\times 100$

$=79\%$

72. By selling a book for ₹50, a shopkeeper suffers a loss of 10%. The cost price of the book is ₹60.

Ans: Its a False statement.

Selling price of a book $=Rs.50$.

Percentage of loss $10\%$.

Now, C.P $=\dfrac{S.P.\times 100}{\left( 100-Loss\% \right)}$

$C.P.=\dfrac{50\times 100}{\left( 100-10 \right)}=\dfrac{5000}{90}$

$=Rs.55.55$

73. If a chair is bought for ₹2000 and is sold at a gain of 10%, then the selling price of the chair is ₹2010.

Ans: Its a False statement.

Cost price of a chair $=Rs.2000$

Percentage gain $=10$%

Here,

 $S.P=\left( 100+\dfrac{gain}{100} \right)\times C.P$

$=\left( \dfrac{100+10}{100} \right)\times 2000$

$S.P=\dfrac{110}{100}\times 2000$

$Rs.2200$

74. If a bicycle was bought for ₹650 and sold for ₹585, then the percentage of profit is 10.

Ans: It's a False statement.

Cost price of a bicycle $=Rs.650$

Selling price of a bicycle $=Rs.585$

Hence, 

Total loss \[=650-585\]

$=Rs.65$

Loss $\% =\dfrac{65}{650}\times 100$

$=10\%$

75. Sushma sold her watch for ₹3320 at a gain of ₹320. For earning a gain of 10% she should have sold the watch for ₹3300.

Ans: Its a True statement.

Selling price of a watch $=Rs.3320$.

Gain at selling price $=Rs.320$

Cost price of a watch $=3320-320$

$=Rs.3000$

Desired gain $=10\%$

Hence, 

$S.P=\left( \dfrac{100+gain\%}{100} \right)\times C.P$ 

$=\left( \dfrac{100+10}{100} \right)\times 3000$

$=\dfrac{110}{100}\times 3000$

$=Rs3300$

76. Interest on ₹1200 for $1\dfrac{1}{2}$ years at the rate of 15% per annum is ₹180.

Ans: It's a False statement.

Given, principal $=Rs1200$

Time $=\dfrac{3}{2}years$

Rate $=15\%$

Now, 

Interest$=\dfrac{principal\times rate\times time}{100}$

Interest$=\dfrac{1200\times 15\times 3}{100\times 2}=270$

So, the interest is $270$.

77. Amount received after depositing ₹800 for a period of 3 years at the rate of 12% per annum is ₹896.

Ans: It's a False statement.

Given- 

Principal $=Rs.800$

 Time $=3yr$

Rate $=12\%$

Now, 

Interest= $\dfrac{principal\times rate\times time}{100}$

Interest= $\dfrac{800\times 12\times 3}{100}=Rs288$

Amount = principal $+$ interest.

Amount\[=\text{ }800+288\]

Amount\[=\text{ }Rs1088\]

78. ₹6400 was lent to Feroz and Rashmi at 15% per annum for $3\dfrac{1}{2}$ and 5 years respectively. The difference in the interest paid by them is ₹150.

Ans: Given 

Feroz borrowed $Rs.6400$ for $3\dfrac{1}{2}year$ at $15\%$.

Here, principal $=Rs.6400$

Time=$3\dfrac{1}{2}=\dfrac{7}{2}year$

Rate $=15\%$

Interest = $\dfrac{principal\times rate\times time}{100}$

$=\dfrac{6400\times 15\times 7}{100\times 2}=Rs3360$

Rashmi borrowed $Rs.6400$ for $5$ years at $15\%$

Here, 

Principal $=Rs.6400$

Time $=5yr$

Rate $=15\%$

Interest =$\dfrac{principal\times rate\times time}{100}$

$=\dfrac{6400\times 15\times 5}{100}=Rs4800$

Difference between interests\[=4800-3360\]

\[=Rs.1440\]

79. A vendor purchased 720 lemons at ₹120 per hundred. 10% of the lemons were found rotten which he sold at ₹50 per hundred. If he sells the remaining lemons at ₹125 per hundred, then his profit will be 16%.

Ans: Given, cost price of $100$ lemons $=Rs.120$

Cost price of $1$ lemon= $Rs\dfrac{120}{100}$

And cost price of $720$ lemon =$\dfrac{120}{100}\times 720=Rs864.$

According to the question $10\%$ of the lemons were rotten.

$10\%$ of $720$ lemons =$\dfrac{10}{100}\times 720=72$lemons.

Also, given the selling price of $100$ rotten lemon $50$.

Selling price of $1$ rotten lemon $=Rs.\dfrac{50}{100}$

And selling price of $72$ rotten lemons=$\dfrac{50}{100}\times 72=36$

Also selling price of $100$ good lemon $=Rs.125$

And the selling price of \[\left( 720-72=648 \right)\]gold lemon.

$\dfrac{125}{100}\times 648=Rs810$

Now, total selling price of $720$ lemons \[=36+810=Rs846\]

Clearly, selling price $<$ cost price.

Therefore, vendors will bear losses.

80. Find the value of x if 

(i) 8% of ₹x is ₹100 

Ans: Given $8\%$ of $x=100$

$\dfrac{8}{100}\times x=100$

$x=\dfrac{100\times 100}{8}$

$x=1250$

(ii) 32% of x kg is 400 kg 

Ans: Given, $32\%$ of $x=400kg$

$=\dfrac{32}{100}\times x=400$

$=x=\dfrac{400\times 100}{32}$

$=1250$

(iii) 35% of ₹x is ₹280 

Ans: Given, $35\%$ of $x=280$

$=\dfrac{35}{100}\times x=280$

$=x=\dfrac{280\times 100}{35}=800$

(iv) 45% of marks x is 405.

Ans: Given, $45\%$ of $x=405$

$=\dfrac{45}{100}\times x=405$

$=x=\dfrac{405\times 100}{45}$

$=x=900$

(a) Shade 25% of the grid. What is 25% of 300? Compare the two answers.

Ans: $25\%$ of $300=\dfrac{25}{100}\times 300=75$

Now, each small square is worth $3$ hence, worth of $25$ squares$=25\times 3=75$

(b) What is the value of 25 squares? 

Ans: from part(a) of the Sol the values of the small square is $75$.

$=25\times 3=75$.

(c) Shade 17% of the grid. What is 17% of 300? Compare the two answers. 

Now, each small square is worth 3 hence, worth of small square $17\times 3=51$

Both the values are the same.

(d) What is the value of $\dfrac{1}{10}$ of the grid?

Ans: Total numbers in grid $=10\times 10=100$

$\therefore \dfrac{1}{10}$of $100=\dfrac{1}{10}\times 100=10$

Now each small square is worth $3$

Hence, worth of $10$ small square 

$=10\times 3=30$

82. Express $\dfrac{1}{6}$ as a percent.

Ans: Given $\dfrac{1}{6}$

In percentage 

$=\dfrac{1}{6}\times 100\%$
$=\dfrac{100}{6}=\dfrac{50}{3}=16.6\%$

83. Express $\dfrac{9}{40}$ as a percent.

Ans: Given,$\dfrac{9}{40}$

In percentage,

$=\dfrac{9}{40}\times 100\%$

$=\dfrac{9}{40}\times 100=\dfrac{900}{40}=22\dfrac{1}{2}\%$

84. Express $\dfrac{1}{100}$ as a percent.

Ans: Given, $\dfrac{1}{100}$

In percentage,

$=\dfrac{1}{100}\times 100\%$

$=\dfrac{100}{100}=1\%$

85. Express 80% as a fraction in its lowest term.

Ans: Given, $80\%$

$=\dfrac{80}{100}=\dfrac{4}{5}$

86. Express $33\dfrac{1}{3}\%$ as a ratio in the lowest term.

Ans: We have, $33\dfrac{1}{3}\%$

For ratio,

$=33\dfrac{1}{3}\%:1$

$=\dfrac{100}{3}\times \dfrac{1}{100}:1$

$=\dfrac{1}{3}:1$

$=\dfrac{1}{3}\times 3:1\times 3$

(both side multiply by $3$)

$=1:3$

87. Express $16\dfrac{2}{3}\%$ as a ratio in the lowest form.

Ans: We have $16\dfrac{2}{3}\%=\dfrac{50}{3}\%$ for the ratio.

$=\dfrac{50}{3}\%:1$

$=\dfrac{50}{3}\times \dfrac{1}{100}:1$

$=\dfrac{1}{6}:1$

$=\dfrac{1}{6}\times 6:1\times 6$

(both side multiply by $6$)

$=1:6$

88. Express 150% as a ratio in the lowest form.

Ans: Given, $150\%$ for ratio,

$=\dfrac{150}{100}:1$

$=\dfrac{3}{2}:1$

$=\dfrac{3}{2}:1$

$=\dfrac{3}{2}\times 2:1\times 2$

(both side multiply by $2$)

$=3:2$

89. Sachin and Sanjana are calculating 23% of 800.  Now calculate 52% of 700 using both the ways described above. Which way do you find easier?

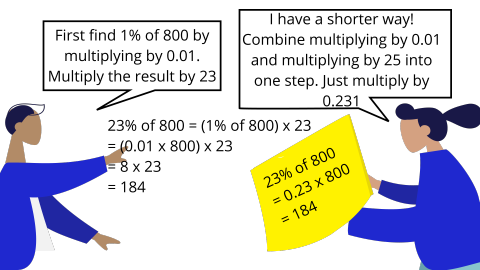
Ans: First way to find $=52\%$ of $700$

Find  1% of 700

$=\left( \dfrac{1}{100}\times 700 \right)$

$=0.01\times 700$

Now multiply it with 52.

$=7\times 52$

$=364$

Second way

$=52\%$ of $700$

$=\dfrac{52}{100}\times 700$

$=0.52\times 700$

$=364$

∴ second way is easier.

90. Write 0.089 as a percent.

Ans: Given, \[0.089\]

In percentage,\[0.089\times 100\%\]

\[=8.9\%\]

91. Write 1.56 as a percent.

Ans: To convert any decimal percentage, we have to multiply that by $100$.

So, as we have $1.56$

That’s why $= 1.56\times 100$

\[=156\%\]

So, $156\%$ is the $\%$ form of base.

92. What is 15% of 20?

Ans: Let x$\%$ of y is z.

i.e.$z=\dfrac{x}{100}\times y$

Here $x\%=15\%,y=20$

So, 

 \[z=\dfrac{15}{100}\times 20\]

\[z=3\]

So, $3$ is the $15\%$ of $20$.

93. What is 800% of 800?

Ans: Let $x\%$ of y is z.

i.e$z=\dfrac{x}{100}\times y$

here \[x=800, y=800\]

so, 

$z=\dfrac{800}{100}\times 800$

$z=6400$

So, $6400$ is the $800\%$ of $800$.

94. What is 100% of 500?

Ans: Let $x\%$ of y is z.

i.e $z=\dfrac{x}{100}\times y$

Here $x=100$ and $y=500$

$z=\dfrac{100}{100}\times 500$

$z=500$

So, $500$ is the $100\%$ of $500$.

95. What percent of 1 hour is 30 minutes?

Ans: Let $x\%$ of y is z. 

i.e $\left[ z=\dfrac{x}{100}\times y \right]$

Here, given $z=30$ minutes 

$y=1$hour$=60$minutes

x=?

$\therefore 30=\dfrac{x}{100}\times 60$

$x=50$

So, $50\%$ of $1$ hour is $30$ minutes. 

96. What percent of 1 day is 1 minute?

Ans: Let x% of y is z.

i.e $z=\dfrac{x}{100}y$

here given $z=1$minute

x=?

y= $1day=24hour=24\times 60$minutes

$y =1440$minutes

$\therefore z=1=\dfrac{x}{100}\times 1440$

$x=0.069$

So,$0.069\%$ of $1$ day is $1$minutes.

97. What percent of 1 km is 1000 metres?

Ans: Let x% of y is z.

i.e. $z=\dfrac{x}{100}\times y$

here, given $z=1000meters$

$y=1km=1000meters$

We know $1km=1000meters$

So, $z=1000=\dfrac{x}{100}\times 1000$

$x=100$

So, $100\%$ of 1km is 1000 meters.

98. Find out 8% of 25 kg.

Ans: Let x% of y is z.

$z=\dfrac{x}{100}\times y$

Here given $x=8,y=25kg$

So, 

$z=\left( \dfrac{8}{100}\times 25 \right)kg$

$z=2kg$

So $2kg$ is the $8\%$ of $25kg$.

99. What percent of ₹80 is ₹100?

Ans: Let x% of y is z.

i.e. $z=\dfrac{x}{100}\times y$

Here given $z=100,y=80$

So, 

$100=\left( \dfrac{x}{100}\times 80 \right)$

$x=125$

So $125\%$ of ₹80 is ₹100.

100. 45% of the population of a town are men and 40% are women. What is the percentage of children?

Ans: Let $100\%$ be the total percentage.

Given, percentage of men $=45$

Percentage of women$=40$

Hence, percentage of children = total % - % of men -% of women

i.e. % of children $=100-(45+40)$ 

$=100-85$

$=15$

So, $15$ is the percentage of children.

101. The strength of a school is 2000. If 40% of the students are girls then how many boys are there in the school?

Ans: Given total numbers of students$=2000$

Number of girls $=40\%$ of total students 

i.e $\dfrac{40}{100}\times 2000$

hence, number of girls$=800$

numbers of boys $=$(total numbers of students $-$ number of girls)

$\Rightarrow 2000-800=1200$

Hence, numbers of boys $=1200$

102. Chalk contains 10% calcium, 3% carbon and 12% oxygen. Find the amount of carbon and calcium (in grams) in $2\dfrac{1}{2}$ kg of chalk.

Ans: Given, total amount of chalk $=2\dfrac{1}{2}kg=\dfrac{5}{2}kg$

And amount of calcium=$10\%$ 

$=\left( \dfrac{10}{100}\times \dfrac{5}{2} \right)kg=0.25kg$ or $250gram(1kg=1000g)$

Amount of carbon$=3\%$ of $\dfrac{5}{2}kg$

$=\left( \dfrac{3}{100}\times \dfrac{5}{2} \right)kg=0.075kg=(0.075\times 1000)gram$

(as we know $1kg=1000gram$)

$=75gram$

So, amount of carbon  $=75gram$

And amount of calcium$=250gram$

103. 800 kg of mortar consists of 55% sand, 33% cement and rest lime. What is the mass of lime in mortar?

Ans: Given, 

Mass of mortar$=800kg$

Mass of lime in mortar=?

Let $100\%$ are the total percentage 

So, $\%$ of lime in mortar=total $\%-$($\%$ of sand$+\%$ of cement)

Given, 

$\%$ of sand $=55$ and $\%$ of cement $=33$

Hence, $\%$ of lime $=[100-(55+33)]$

$=12$

Now, 

mass of lime $=12\%$ of $800kg$

$=\left( \dfrac{12}{100}\times 800 \right)kg$

$=96kg$

So, mass of lime is $96kg$

104. In a furniture shop, 24 tables were bought at the rate of ₹450 per table. The shopkeeper sold 16 of them at the rate of ₹600 per table and the remaining at the rate of 400 per table. Find her gain or loss percent.

Ans: Given,

 Cost price of $1table=Rs.450$

Hence, cost price of 24 tables $=\left( 24\times 450 \right)$

$=10800$

Selling price of $16$ tables= $\left( 16\times 600 \right)=Rs.9600$

Selling price of $8$ tables= $\left( 8\times 400 \right)=Rs.3200$

Selling price of $24$ tables $=Rs.\left( 9600+3200 \right)$

$=Rs.12800$

Here, $S.P.\left( 12800 \right)>c.p.(10800)$

Therefore, gain of $=\left( 12800-10800 \right)=2000$

Gain \[\%\] $=\dfrac{2000}{10800}\times 100=18.5$

So, $\%$ gains is $18.5\%$

105. Medha deposited 20% of her money in a bank. After spending 20% of the remainder, she has ₹4800 left with her. How much did she originally have?

Ans: Let “x” be the amount of money 

Given, amount of money deposited =$20\%$ of x

$=\dfrac{20}{100}x=\left( \dfrac{x}{5} \right)$

Remaining amount $=\left( x-\dfrac{x}{5} \right)=\left( \dfrac{4}{5} \right)x$

Amount of money spent by her $=20\%$ of $\dfrac{4}{5}x$

$=\dfrac{20}{100}\times \dfrac{4}{5}x=\dfrac{4}{25}x$

Amount of money left with her,

$=\dfrac{4}{5}x-\dfrac{4}{25}x$

$=\left( \dfrac{16}{25}x \right)$

According to question 

$\dfrac{16}{25}x=4800$

$x=7500$

So, $Rs7500$ is the amount which she originally had. 

106. The cost of a flower vase got increased by 12%. If the current cost is ₹896, what was its original cost?

Ans: Let the original cost be x.

Now the cost of flower vase is increased by $12\%$

So,  $x+12\%$ of x=$896$

$\Rightarrow x+\dfrac{12x}{100}=896$

$\Rightarrow \dfrac{112x}{100}=896$

$\Rightarrow x=\dfrac{896\times 100}{112}$

$\Rightarrow x=800$

Hence the original cost of the flower vase is $Rs.800$.

107. Radhika borrowed ₹12000 from her friends. Out of which ₹4000 were borrowed at 18% and the remaining at 15% rate of interest per annum. What is the total interest after 3 years?

Ans: For first year interest we have.

Principal $=4000$ 

Rate= $18\%$ 

Time$=3year$

$\operatorname{int}rest=\dfrac{P\times R\times T}{100}$

$I=\dfrac{4000\times 18\times 3}{100}=2160Rs$

For second year interest

$P=12000-4000=8000$

$R=15\%$

$T=3$Year

${{I}_{2}}=\dfrac{P\times R\times T}{100}$

${{I}_{2}}=\dfrac{8000\times 15\times 3}{100}=3600Rs$

Total interest

${{I}_{1}}+{{I}_{2}}=2160+3600=5760$ 

108. A man travelled 60 km by car and 240 km by train. Find what percent of total journey did he travel by car and what percent by train?

Ans: Given 

Travel by car $=60km$

Travel by train $=240km$

Total travel by man $=60+240=300km$

Now first of all calculate $\%$ by travel car.

$\dfrac{60}{300}\times 100=20\%$

∴ Percentage by travel.

$\dfrac{240}{300}\times 100=80\%$

109. By selling a chair for ₹1440, a shopkeeper loses 10%. At what price did he buy it?

Ans: Given S.P. $=1440$ and loss $=10\%$

We know that 

loss$\%=\dfrac{Loss}{C.P.}\times 100\%$

$\Rightarrow Loss\%=\dfrac{C.P.-S.P.}{C.P.}\times 100\%$

$\Rightarrow 10=\dfrac{C.P.-1440}{C.P.}\times 100$

$\Rightarrow \dfrac{1}{10}=\dfrac{C.P.-1440}{C.P.}$

$C.P.=10 C.P. - 10 \times 1440$

$C.P.=\dfrac{1440\times 10}{9}$

$C.P.=1600Rs$

110. Dhruvika invested money for a period from May 2006 to April 2008 at a rate of 12% per annum. If interest received by her is ₹1620, find the money invested.

Ans: Given-

Interest$=1620Rs$, Rate$=12\%$

Time from May 2006 to April 2008 $=2year$

Now find principle 

$\because Interest=\dfrac{\Pr inciple\times Rate\times Time}{100}$

$=\Pr inciple=\dfrac{Interest \times 100}{Rate\times Time}$

$P=\dfrac{1620\times 100}{12\times 2}$

$P=6750Rs$

Hence, the invested money is $6750Rs$.   

111. A person wanted to sell a scooter at a loss of 25%. But at the last moment he changed his mind and sold the scooter at a loss of 20%. If the difference in the two SP’s is ₹4000, then find the CP of the scooter.

Ans: Let the cost of the scooter be $=X$.

If he sells the scooter at a loss of $25\%$ then

$SP=X-25\%$ of $X=\dfrac{X-25}{100}=\dfrac{75}{100}x$

And if he sells the scooter at a loss of $20\%$

$SP=x-20\%$ of $x=x-\dfrac{20}{100}x=\dfrac{80x}{100}$

It is given that the difference in the two SP is $4000Rs$

$\dfrac{80}{100}x-\dfrac{75x}{100}=4000$

$\dfrac{80x-75x}{100}=4000$

$\dfrac{5x}{100}=4000$

$x=80,000Rs$

112. The population of a village is 8000. Out of these, 80% are literate and of these literate people, 40% are women. Find the ratio of the number of literate women to the total population.

Ans: We have total population$=8000$

Literate people $=80\%$ of total population

$\dfrac{80}{100}\times 8000=6400$

Literate women$=40\%$ of literate people

$=\dfrac{40}{100}\times 6400=2560$

Ratio of literate women to total population

$=2560:8000$

 $=\dfrac{2560}{320}:\dfrac{8000}{320}=8:25$

113. In an entertainment programme, 250 tickets of ₹400 and 500 tickets of ₹100 were sold. If the entertainment tax is 40% on a ticket of ₹400 and 20% on a ticket of ₹100, find how much entertainment tax was collected from the programme.

Ans: It is given that $250$ ticket of $400$ were sold.

Therefore total amount received by selling these tickets $=250\times 400=100000.$

Similarly amount received by selling $500$ tickets of $100Rs$

$=500\times 100=50000Rs$

It is also given that $40\%$ and $20\%$ of entertainment tax is on $400Rs$ and $100Rs$ tickets respectively.

So total entertainment tax collected 

$=40\%$ of total amount received by selling tickets of $400+20\%$ total amount received by selling tickets of $100Rs$

$=40\%$ of $100000+20\%$ of $50000$

$=\dfrac{40}{100}\times 100000+\dfrac{20}{100}\times 50000$

$=40000+10000$

$=50000Rs$

114. Bhavya earns ₹50,000 per month and spends 80% of it. Due to pay revision, her monthly income increases by 20% but due to price rise, she has to spend 20% more. Find her new savings. 

Ans: Given

Bhavya earns per month $=50000Rs$

She spends per month

$=80\%$ of $50000$

$=\dfrac{80}{100}\times 50000=40000 Rs$

Then her per month saving 

\[=50000-40000\]

\[=10000Rs\]

Also, given increment in monthly income

$=20\%$ of $50000$

$=\dfrac{20}{100}\times 50000=10000Rs$

∴ bhavya new income $=50000+10000=60000Rs$

Increase in expenditure

 $=20\%$ of $40000$

$=\dfrac{20}{100}\times 40000=8000$

So new expenditure $=Rs(40000+8000)=48000Rs$

Now bhavya’s new saving

 $=60000-48000$

$=12000Rs$

115. In an examination, there are three papers each of 100 marks. A candidate obtained 53 marks in the first and 75 marks in the second paper. How many marks must the candidate obtain in the third paper to get an overall of 70 per cent marks?

Ans: Let X be the marks of the candidate in the third paper.

Then total marks secured in all those papers$=53+75+x$

Total marks of three papers$=100+100+100=300$

∴ percentage of marks

 $=\left( \dfrac{\text{Total secured marks}}{\text{Total Marks}}\right)\times 100\%$

$=\dfrac{53+75+x}{300}\times 100$

But it is given that he obtained over all of $70\%$ marks

$\therefore \dfrac{53+75+x}{300}\times 100=70$

$\Rightarrow \dfrac{128+x}{3}=70$

$\Rightarrow 128+x=210$

$x=82$

Hence he must secure 82 marks in the third paper to get an overall of  $70\%$marks.

116. Health Application A doctor reports blood pressure in millimetres of mercury (mm Hg) as a ratio of systolic blood pressure to diastolic blood pressure (such as 140 over 80). Systolic pressure is measured when the heart beats, and diastolic pressure is measured when it rests. Refer to the table of blood pressure ranges for adults.

Manohar is a healthy 37 years old man whose blood pressure is in the normal category. 

(a) Calculate an approximate ratio of systolic to diastolic blood pressures in the normal range. 

Ans: Given data of Blood pressure ranges

Normal systolic blood pressure $=120mmHg$

Diastolic blood pressure $=80mmHg$

So, the required ratio $=\dfrac{120}{80}$

$=\dfrac{3}{2}$

(b) If Manohar’s systolic blood pressure is 102 mm Hg, use the ratio from part (a) to predict his diastolic blood pressure. 

Ans: Given, Manohar’s systolic blood pressure $=102mm$

So, the diastolic blood pressure $=\dfrac{102}{\text{diastolic blood pressure}}=\dfrac{3}{2}$

Diastolic blood pressure $=102\times \dfrac{2}{3}$

$=68mm$

(c) Calculate ratio of average systolic to average diastolic blood pressure in the prehypertension category. 

Ans: For calculating average in prehypertension conditions

Average for systolic pressure in the prehypertension category $=\dfrac{120+139}{2}=\dfrac{259}{2}$

Average for diastolic blood pressure in the prehypertension category $=\dfrac{80+89}{2}=\dfrac{169}{2}$

Required ratio $=\dfrac{\dfrac{252}{2}}{\dfrac{169}{2}}=\dfrac{252}{169}$

117. (a) Science Application: The king cobra can reach a length of 558 cm. This is only about 60 per cent of the length of the largest reticulated python. Find the length of the largest reticulated python.

Ans: Let x cm is the length of the largest reticulated python

$60\%$of $x=558$

$\Rightarrow \dfrac{60}{100}\times x=558$

$x=\dfrac{558\times 100}{60}$

$x=930$

(b) Physical Science Application: Unequal masses will not balance on a fulcrum if they are at equal distance from it; one side will go up and the other side will go down. Unequal masses will balance when the following proportion is true: 

$\dfrac{\text { mass } 1}{\text { length } 2}=\dfrac{\text { mass } 2}{\text { length } 1}$

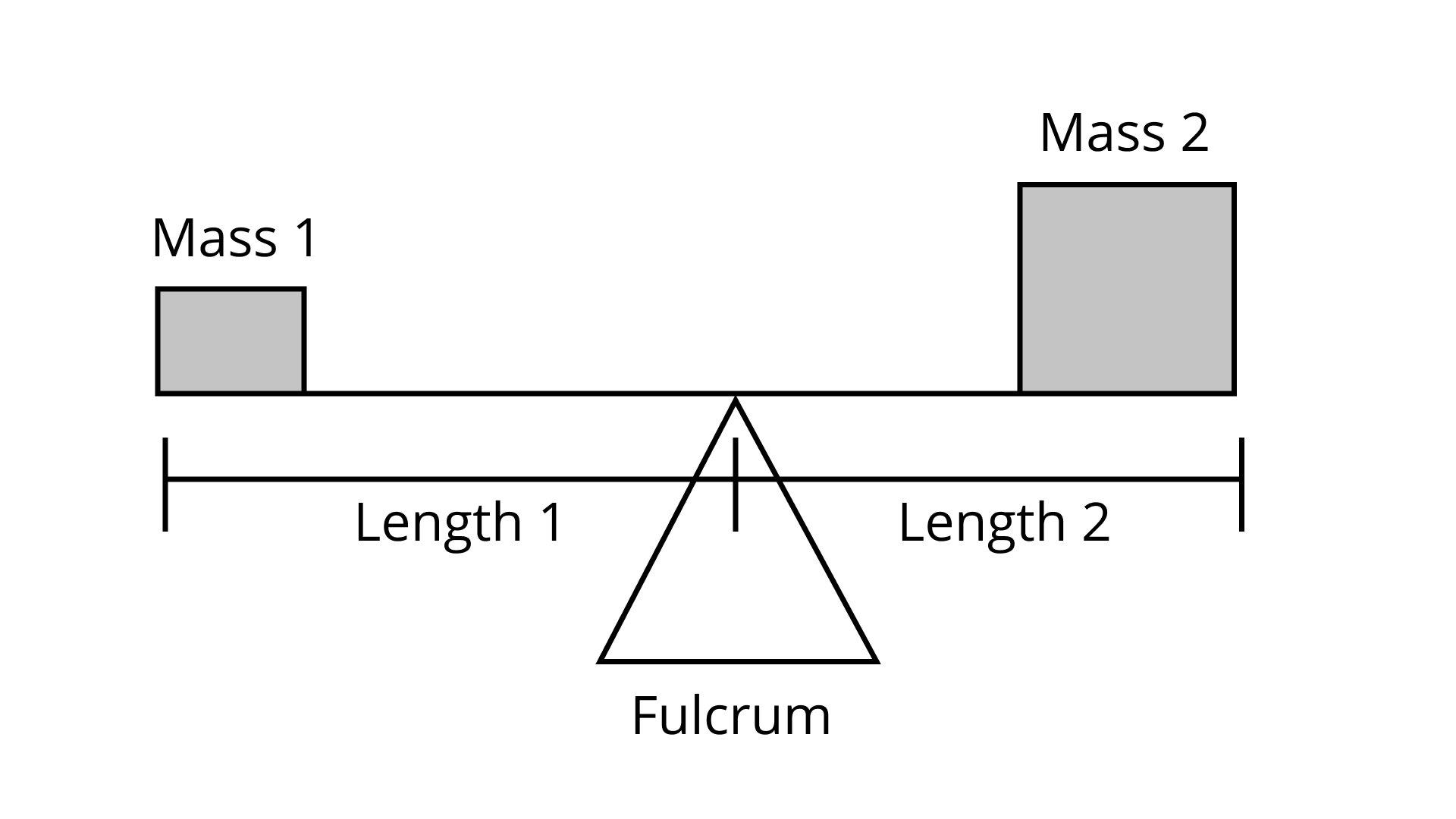
The child on the left and child on the right are balanced. What is the mass of the child on the right?

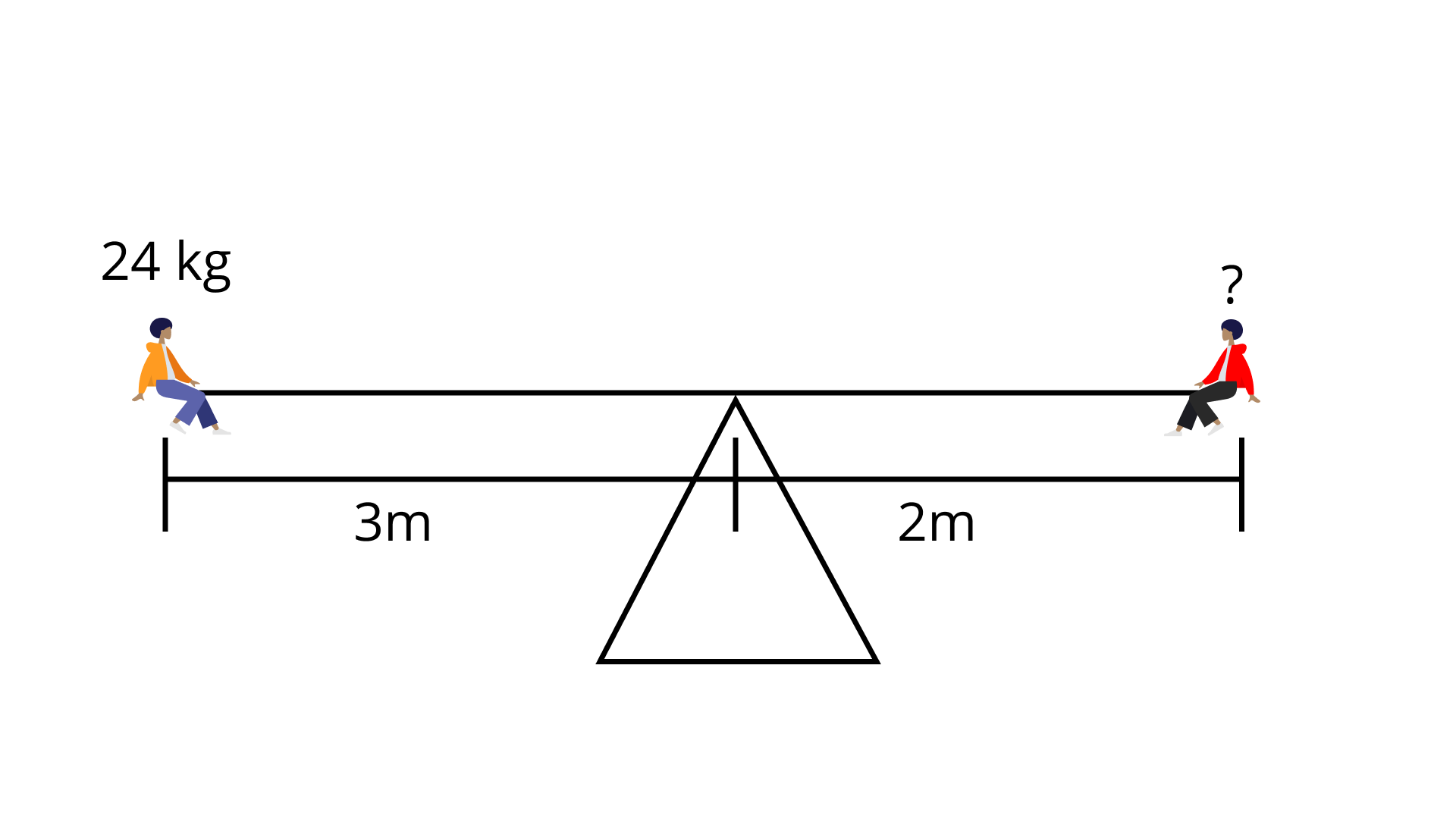
Ans: We know 

$\dfrac{\text { mass } 1}{\text { length } 2}=\dfrac{\text { mass } 2}{\text { length } 1}$

$m_1=24,l_1=3m$

$m_2=?,l_2=2m$

$\dfrac{m_1}{l_2}=\dfrac{m_2}{l_1}$

$m_2=\dfrac{m_1\times l_1}{l_2}$

$m_2=\dfrac{24\times 3}{2}=36kg$

$m_2=36kg$

(c) Life Science Application A DNA model was built using the scale 2 cm : 0.0000001 mm. If the model of the DNA chain is 17 cm long, what is the length of the actual chain?

Ans: Let the actual length of the chain is L.

We know that if the length of the actual chain is $=0.0000001mm$ then it is measured as $2cm$ in the model.

Hence, the length of actual chain when length of chain is $17cm$ in the model

$L=\dfrac{0.0000001}{2}\times 17$

$L=0.00000085mm$

So, the actual length of the chain is $0.00000085mm$.

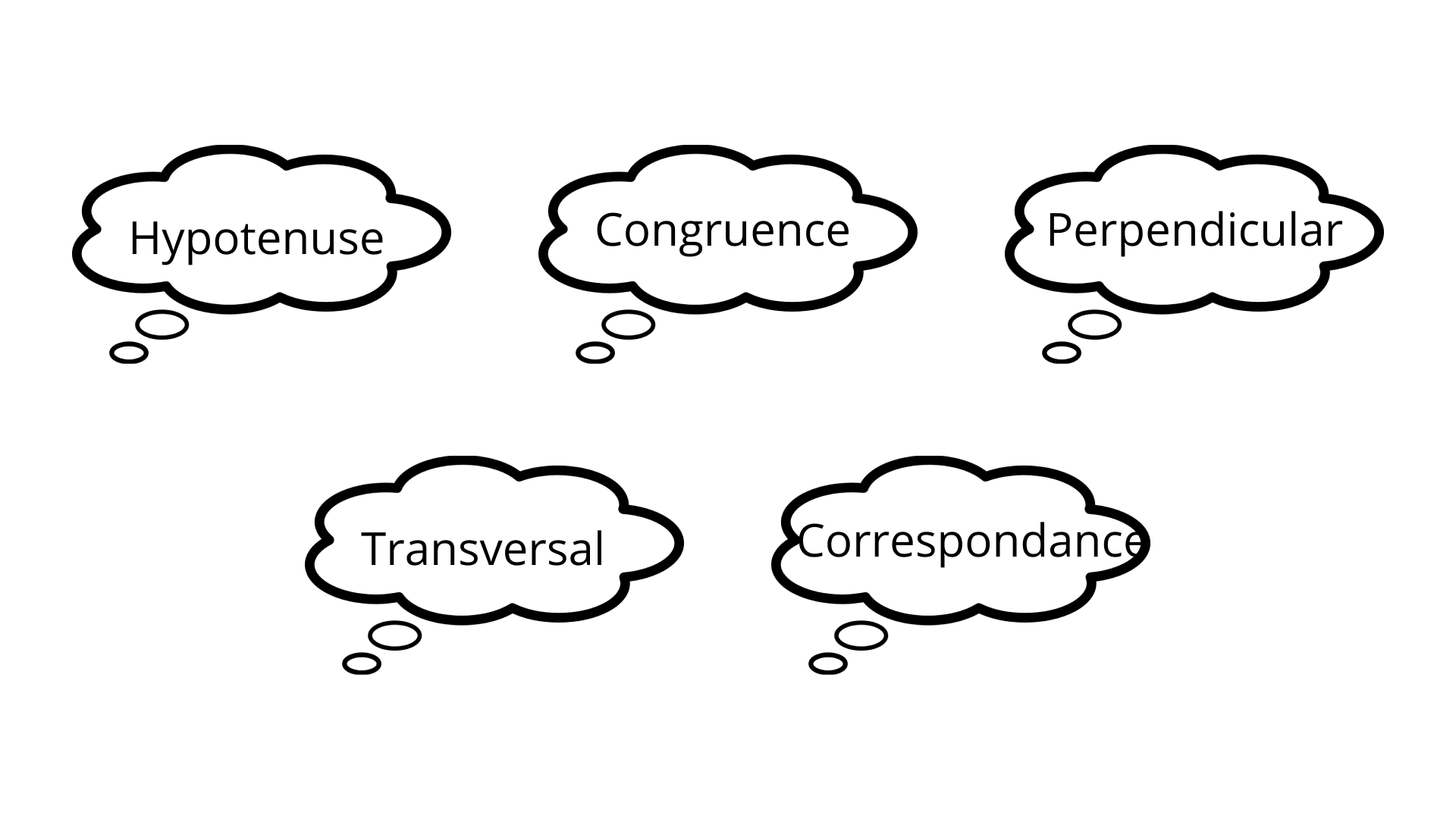
118. Language Application Given below are few Mathematical terms. 

Find

(a) The ratio of consonants to vowels in each of the terms. 

Ans: (i) number of constants in Hypotenuse $=6$

Number of vowel in hypotenuse $=4$

Hence, the ratio of constants to vowel

$=\dfrac{6}{4}=\dfrac{3}{2}$i.e. $3:2$

(ii) number of constants in congruence $=6$

Number of vowel in congruence $=4$

Hence, the ratio of constants to vowel $=\dfrac{6}{4}=\dfrac{3}{2}$

i.e. $3:2$

(iii) number of constants in perpendicular $=8$

Number of vowel in perpendicular $=5$

Hence, required ratio $=\dfrac{8}{5}$i.e. $8:5$

(iv)  number of constants in transversal $=8$

Number of vowel in transversal  $=3$

Hence, required ratio $=\dfrac{8}{3}$i.e. $8:3$

(v) number of constants in Correspondence $=9$

Number of vowel in Correspondence $=4$

Hence, required ratio $=\dfrac{9}{4}$i.e. $9:4$

(b) The percentage of consonants in each of the terms.

Ans: (i) percentage of constants in Hypotenuse 

$=\dfrac{6}{100}\times 100=\dfrac{600}{10}=60\%$

(ii) percentage of constants in congruence 

$=\dfrac{6}{100}\times 100=\dfrac{600}{10}=60\%$

(iii) Percentage of constants in perpendicular  

$\dfrac{8}{13}\times 100=\dfrac{800}{13}=61.53\%$

(iv) percentage of constants in Hypotenuse 

$=\dfrac{6}{100}\times 100=\dfrac{600}{10}=60\%$

(v) percentage of constants in ‘’transversal’’

$=\dfrac{8}{11}\times 100=\dfrac{800}{11}=72.72\%$

(vi) percentage of constants in correspondence

$=\dfrac{9}{14}\times 100=\dfrac{900}{14}=64.28\%$

119. What is the Error? An analysis showed that 0.06 per cent of the T-shirts made by one company were defective. A student says this is 6 out of every 100. What is the student’s error? 

Ans: Given,

Percentage of T-shirt $=0.06\%$

$0.06\%=\dfrac{.06}{100}$

$=\dfrac{6}{10000}$

Therefore, $10000$ are the total t-shirt instead of 100.

120. What’s the Error? A student said that the ratios 3:4 and 9:16 were proportional. What error did the student make? 

Ans: Two ratio $a:b$ and $c:b$ are said to be proportional 

If $\dfrac{a}{b}=\dfrac{c}{d}$ or $ad=bc$.

But the given ratios $\dfrac{3}{4}\And \dfrac{9}{16},3\times 16\ne 4\times 9$

Hence, the ratios are not proportional. To make a ratio proportional to another ratio, we just simply multiply both numerator and denominator by the same number. Here, the student had multiplied the numerator by 3 and the denominator by 4, which is incorrect.

121. What’s the Error? A clothing store charges ₹1024 for 4 T-shirts. A student says that the unit price is ₹25.6 per T-shirt. What is the error? What is the correct unit price? 

Ans: By unitary method,

Cost of 4 T-shirt $=1024$

Cost of 1 T-shirt$=\dfrac{1024}{4}=256Rs$

According to the student, the unit price is $25.6Rs$ Which is wrong.

Hence the correct unit price is $=256$

122. A tea merchant blends two varieties of tea in the ratio of 5: 4. The cost of the first variety is ₹200 per kg and that of the second variety is ₹300 per kg. If he sells the blended tea at the rate of ₹275 per kg, find out the percentage of her profit or loss. 

Ans: Given, ratio of blended two vertices of tea $=5:4$

Cost of first variety of tea$=200$per kg

Cost of second variety of tea $=300$per kg

SP of blended tea =$275$per kg

According to the ratio,

Let first variety of tea be $5x$kg and second variety of tea be $4x$kg

Then cost of first variety of tea $=5x\times 200=1000x$

Cost of second variety of tea $=4x\times 300=1200x$

Total quantity $=4x+5x=9x$kg

So, for $3x$kg

SP of blended tea $=275\times 9x=2475x$

$\therefore C.P<S.P$

So, there is profit on blended tea 

Profit $=$S.P.$-$C.P

$=2475x-2200x=275x$

Profit $\%=\dfrac{profit}{CP}\times 100\%=\dfrac{275x}{2200x}\times 100\%$

$=\dfrac{275}{22}=12.56$

Hence, there is $12.5\%$ profit on blended tea.

123. A piece of cloth 5 m long shrinks 10 percent on washing. How long will the cloth be after washing? 

Ans: Length of shrink cloth 

$10\%$of $5m=\dfrac{10}{100}\times 5$

$=\dfrac{1}{2}m$

$\therefore $length of cloth after wash $=5-\dfrac{1}{2}=\dfrac{9}{2}$

$=4.5m$

124. Nancy obtained 426 marks out of 600 and the marks obtained by Rohit are 560 out of 800. Whose performance is better? 

Ans: Nancy got marks$=426$ out of $600$

Percentage marks$=\dfrac{426}{600}\times 100\%=71\%$

Rohit got marks $=560$ out of $800$

Percentage marks $=\dfrac{560}{800}\times 100\%=70\%$

Hence, Nancy's performance is better, since She got $1\%$ more than rohit.

125. A memorial trust donates ₹5, 00,000 to a school, the interest on which is to be used for awarding 3 scholarships to students obtaining first three positions in the school examination every year. If the donation earns an interest of 12 per cent per annum and the values of the second and third scholarships are ₹20,000 and ₹15,000 respectively, find out the value of the first scholarship. 

Ans: Step-1

Donation amount is $Rs500000$

The rate of interest for each year is $12\%$ per annum.

Calculation:-

Interest received 

$=500000\times 12\%$

$=500000\times \dfrac{12}{100}=60000$

Step-2

Scholarship amount for second position is $Rs20000$ and the scholarship amount for the third position is $Rs15000$

Calculation :-

Scholarship amount for first position 

$=60000-20000-15000$

$=Rs25000$

126. Ambika got 99 percent marks in Mathematics, 76 percent marks in Hindi, 61 percent in English, 84 percent in Science, and 95% in Social Science. If each subject carries 100 marks, then find the percentage of marks obtained by Ambika in the aggregate of all the subjects. 

Ans: It is given that, each subject carries $100$mark 

$\therefore $Ambika got marks in mathematics $=99$

Hindi $=76$

English $=61$

Science $=84$

Social science $=95$

Now, aggregate percentage of marks 

$\Rightarrow \dfrac{\text{Obtained marks}}{\text{Total marks}}\times 100\%$

$\Rightarrow \dfrac{\left( 99+76+61+84+95 \right)}{500}\times 100\%=\dfrac{415}{500}=83\%$

127. What sum of money lent out at 16 per cent per annum simple interest would produce ₹9600 as interest in 2 years? 

Ans: Given, Interest $=Rs9600$

Time $=2yr$

Rate $=16\%$

$\because $ interest $=\dfrac{\Pr incipal\times Rate\times Time}{100}$

$\because $ Principal$=\dfrac{Interest\times 100}{Rate\times Time}$

$\therefore $ Principal $=\dfrac{9600\times 100}{16\times 2}$

$\therefore $ Principal $=30000Rs$

128. Harish bought a gaschullah for ₹900 and later sold it to Archana at a profit of 5 per cent. Archana used it for a period of two years and later sold it to Babita at a loss of 20 per cent. For how much did Babita get it? 

Ans: It is given that Harish bought the gas-chullah for $Rs900$and sold it to Archana at a profit of $5\%$.

$\therefore $Cost price of gas chullah for Archana 

$\Rightarrow 900+5\%$ of $900$

$\Rightarrow 900+\dfrac{5}{100}\times 900$

$900+45$

$\Rightarrow Rs945$

Now, Archana sold it to Babita at a loss of $20\%$

$\therefore $cost price of gas challah for Babita

$\Rightarrow 945-20\%$of $945$

$\Rightarrow 945-\dfrac{20}{100}\times 945$

$\Rightarrow 945-189$

$\Rightarrow 756Rs$

Hence, Babita got gas challah at Rs. 756.

129. Match each of the entries in Column I with the appropriate entries in Column II:

Ans: (i) Matches to E

Given, ratio $=3:5$

In percentage, $\dfrac{3}{5}\times 100\%=60\%$

(ii) Matches to H

Given, $2.5$

In percentage, $2.5\times 100\%=250\%$

(iii) Matches to O 

Given, $100\%$

$\Rightarrow $Ratio$=100\%:1$

$\Rightarrow \dfrac{100}{100}:1$

Ratio $=1:1$

$1\times 3:1\times 3=3:3$

(iv) Matches to J

Given, $\dfrac{2}{3}$

In percentage, $\dfrac{2}{3}\times 100\%=66\dfrac{2}{3}\%$

(v) matches to G

Given, $6\dfrac{1}{4}\%=\dfrac{25}{4}\%$

For fraction, $\dfrac{25}{4}\times \dfrac{1}{100}=\dfrac{1}{16}$

(vi) Matches to L 

Given, $12.5\%$

For fraction, $\dfrac{125}{10}\times \dfrac{1}{100}=\dfrac{125}{1000}$

For decimal, $\dfrac{125}{1000}=0.125$

(vii) Matches to B

Given, CP=$50$, loss $\%=6\%$

$loss\%=\dfrac{loss}{CP}\times 100\%$

$loss\%=\dfrac{\left( CP-SP \right)}{CP}=100\%$

$\Rightarrow 6=\dfrac{\left( 50-SP \right)}{50}\times 100$

$\Rightarrow SP=47$

(viii) Matches to A 

Given, CP$=50$, profit $=4$

Profit= SP-CP

SP=Profit$+$CP

SP$=4+50$

SP$=54$

(ix) Matches to F

Given, CP$=40$, SP$=50$

Profit=SP$-$CP

$=50-40$

$=10$

Profit$\%=\dfrac{profit}{CP}\times 100\%$

$=\dfrac{10}{40}\times 100\%$

Profit $=25\%$

(x) Matches to K

Given, $CP=50$, $SP=60$

Profit $=SP-CP$

$=60-50$
$=10$

Profit$\%=\dfrac{\Pr ofit}{CP}\times 100\%$

$=\dfrac{10}{50}\times 100\%$

profit$\%=20\%$

(xi) Matches to D

Given, $P=800,R=10\%,T=2yr$

$\Rightarrow I=\dfrac{P\times t\times R}{100}$

$\Rightarrow I=\dfrac{800\times 2\times 10}{100}$

$\Rightarrow I=160$

(xii) Matches to I

Given, $P=150,R=6\%,T=1yr$

Need to find out amount

$\Rightarrow I=\dfrac{150\times 6\times 1}{100}$

$\Rightarrow I=9$

Amount $=$principal $+$Interest 

$=150+9$

$=Rs.159$

130. In a debate competition, the judges decide that 20 percent of the total marks would be given for accent and presentation. 60 percent of the rest are reserved for the subject matter and the rest are for rebuttal. If this means 8 marks for rebuttal, then find the total marks. 

Ans: Let X be the total marks

Marks given for accent and presentation

$20\%$ of X$=\dfrac{20}{100}\times x=\dfrac{x}{5}$

Remaining marks $=x-\dfrac{x}{5}=\dfrac{4x}{5}$

Marks reserved for subject matter$=60\%$of rest marks 

$\Rightarrow \dfrac{60}{100}\times \dfrac{4x}{5}=\dfrac{12x}{25}$

Now, remaining marks 

$\Rightarrow \dfrac{4x}{5}-\dfrac{12x}{5}=\dfrac{20x-12x}{25}=\dfrac{8x}{25}$

According to the question

$\Rightarrow \dfrac{8x}{25}=8$

$\Rightarrow x=\dfrac{8\times 25}{8}=25$

Hence, total marks are $25$.

131. Divide ₹10000 in two parts so that the simple interest on the first part for 4 years at 12 percent per annum may be equal to the simple interest on the second part for 4.5 years at 16 per cent per annum. 

Ans: Given, money$=10000$

Money should be divided into two parts, SI on the first for $4yr$ at $12\%$ and SI on the second part for $4.5yr$ at $16\%$.

Let first part $=x$

Second part $=\left( 10000-x \right)$

$\Rightarrow SI_1=\dfrac{P_1\times R_1\times T_1}{100}=\dfrac{x\times 12\times 4}{100}$

$\Rightarrow SI_2=\dfrac{P_2\times R_2\times T_2}{100}=\dfrac{\left( 10000-x \right)\times 16\times 4.5}{100}$

$\Rightarrow \dfrac{x\times 12\times 4}{100}=\dfrac{\left( 10000-x \right)\times 16\times 4.5}{100}$

$\Rightarrow \dfrac{48x}{4.5\times 16}=\left( 10000-x \right)$

$\Rightarrow \dfrac{48x\times 10}{45\times 16}=\left( 10000-x \right)$

$\Rightarrow \dfrac{2x}{3}=10000-x$

$\Rightarrow \dfrac{5x}{3}=10000$

$\Rightarrow x=6000$

First part $=6000Rs$

Second part $=\left( 10000-x \right)$

$=10000-6000=4000Rs$

132. ₹9000 becomes ₹18000 at simple interest in 8 years. Find the rate per cent per annum. 

Ans: Given, 

$P=9000Rs$

$A=18000Rs$

$T=8yr$

As we know that $A=P+I$

$\Rightarrow I=A-P$

$\Rightarrow I=18000-9000$

$\Rightarrow I=9000Rs$

Now, $I=\dfrac{P\times R\times T}{100}$

$R=\dfrac{I\times 100}{P\times T}=\dfrac{9000\times 100}{9000\times 8}$

$R=12.5\%$

Hence, the rate of interest per annum is $12.5\%$.

133. In how many years will the simple interest on a certain sum be 4.05 times the principal at 13.5 percent per annum? 

Ans: Let principal $=P$, $R=13.5\%$

Need to find T

We know that, $I=\dfrac{P\times R\times T}{100}$

$\Rightarrow 4.05\times P=\dfrac{P\times 13.5\times T}{100}$

$\Rightarrow T=\dfrac{405P}{P\times 13.5}$

$\Rightarrow T=\dfrac{405\times 10}{135}$

$T=30$year

134. The simple interest on a certain sum for 8 years at 12 per cent per annum is ₹3120 more than the simple interest on the same sum for 5 years at 14 per cent per annum. Find the sum.

Ans: Given, ${{I}_{1}}-{{I}_{2}}=3120Rs$

${{T}_{1}}=8yr,{{R}_{1}}=12\%$

${{T}_{2}}=5yr,{{R}_{2}}=14\%$

And ${{P}_{1}}={{P}_{2}}=P$

According to the question, 

${{I}_{1}}-{{I}_{2}}=3120Rs$

$\Rightarrow \dfrac{{{P}_{1}}\times {{R}_{1}}\times {{T}_{1}}}{100}-\dfrac{{{P}_{2}}\times {{R}_{2}}\times {{T}_{2}}}{100}=3120$

$\Rightarrow \dfrac{P\times 12\times 8}{100}-\dfrac{P\times 14\times 5}{100}=3120$

$\Rightarrow \dfrac{P}{100}\left[ 12\times 8-14\times 5 \right]=3120$

$\Rightarrow P\left[ 96-70 \right]=3120\times 100$

$\Rightarrow 26P=312000$

$\Rightarrow P=\dfrac{312000}{26}$

$\Rightarrow P=12000Rs$

Hence, the sum is $12000Rs$.

135. The simple interest on a certain sum for 2.5 years at 12 per cent per annum is ₹300 less than the simple interest on the same sum for 4.5 years at 8 per cent per annum. Find the sum. 

Ans: Let the sum be x

Given that,

${{P}_{1}}=x,{{R}_{1}}=12\%$ and ${{T}_{1}}=2.5yr=\dfrac{5}{2}yr$

And

${{P}_{2}}=x,{{R}_{2}}=8\%$ and ${{T}_{2}}=4.5yr=\dfrac{9}{2}yr$

According to the question,

${{I}_{2}}-{{I}_{1}}=300$

$\Rightarrow \dfrac{{{P}_{2}}\times {{R}_{2}}\times {{T}_{2}}}{100}-\dfrac{{{P}_{1}}\times {{R}_{1}}\times {{T}_{1}}}{100}=300$

$\Rightarrow \dfrac{x\times 8\times 9}{2\times 100}-\dfrac{x\times 12\times 5}{2\times 100}=300$

$\Rightarrow 72x-60x=300\times 200$

$\Rightarrow 12x=60000$

$\Rightarrow x=5000Rs$

136. Designing a Healthy Diet When you design your healthy diet, you want to make sure that you meet the dietary requirements to help you grow into a healthy adult. As you plan your menu, follow the following guidelines 

1. Calculate your ideal weight as per your height from the table given at the end of this question. 

2. An active child should eat around 55.11 calories for each kilogram-desired weight. 

3. 55 percent of calories should come from carbohydrates. There are 4 calories in each gram of carbohydrates. 

4. 15 percent of your calories should come from proteins. There are 4 calories in each gram of proteins. 

5. 30 percent of your calories may come from fats. There are 9 calories in each gram of fat. 

(i)Your ideal desired weight is __________ kg.

Ans: Given,

Let $5$ feet is the height of a girl student

The ideal weight is $45kg$

(ii) The quantity of calories you need to eat is _______.

Ans: Quantity of calories needed $45\times 55.11=2479.95$calories

(iii) The quantity of protein needed is ________ g.

Ans: Calories come from proteins 

$=\dfrac{2479.95\times 15}{100}=371.99$Calories

Quantity of proteins needed

$=\dfrac{371.99}{4}=92.99gm$

(iv) The quantity of fat required is ___________ g. 

Ans: Calories come from fat 

$=\dfrac{2479.95\times 30}{100}=743.985$Calories

Quantity of fat needed

$=\dfrac{743.985}{9}=85.66gm$

(v)  The quantity of carbohydrates required is __________ g.

Ans: Calories come from carbohydrates 

$=\dfrac{2479.95\times 55}{100}=2479.95\times 0.55$

$=1363.97$Calories

Quantity of carbohydrates needed

$\Rightarrow \dfrac{1363.97}{4}=340.99gm$

137. 150 students are studying English, Maths or both. 62 percent of students study English and 68 percent are studying Maths. How many students are studying both?

Ans: Total students $=150$

Students who study maths$=68\%$ of $150$

$\Rightarrow \dfrac{68}{100}\times 150=102$

Students who study English$=62\%$ of $150$

$\Rightarrow \dfrac{62}{100}\times 150=93$

Total students studying English and maths $=93+102=195$

$\therefore $Students who study English and Maths

$\Rightarrow 195-150$

$\Rightarrow 45$

138. Earth Science: The table lists the world’s 10 largest deserts. 

(a) What are the mean, median and mode of the areas listed? 

Ans: mean $=\dfrac{\text{Total area of all deserts}}{\text{No. of deserts}}$

Total area of all deserts

$=8800000+1300000+1250000+850000+580000+370000+320000+310000+310000+260000=14350000$

$\Rightarrow $ mean $= \dfrac{14350000}{10}=1435000k{{m}^{2}}$

Median $=\dfrac{\left[ \left( \dfrac{N}{2} \right)term+\left( \dfrac{N}{2}+1 \right)term \right]}{2}$

$=\dfrac{\left[ \left( \dfrac{10}{2} \right)term+\left( \dfrac{10}{2}+1 \right)term \right]}{2}$

$=\dfrac{\left( 5t{{h}_{{}}}term+6t{{h}_{{}}}term \right)}{2}$

$=\dfrac{580000+370000}{2}=475000k{{m}^{2}}$

Mode$=$Most frequent observation

$=310000k{{m}^{2}}$

(b) How many times the size of the Gobi Desert is the Namib Desert? 

Ans: Let the size of the Gobi desert is X times the Namib desert 

$\therefore $Gobi desert$=X\times $Namib desert

$\Rightarrow 1300000=X\times 310000$

$\Rightarrow X=\dfrac{1300000}{310000}$

$\Rightarrow 4.19$

(c) What percentage of the deserts listed are in Asia? 

Ans: Total number of Desert $=10$

5 Deserts listed in Asia

$\therefore$ Percentage $=\dfrac{5}{10} \times 100=50 \%$

(d) What percentage of the total area of the deserts listed is in Asia? 

Ans: Total area of Deserts listed in Asia, $=1300000+850000+320000$ $+310000+260000=3040000 \mathrm{~km}^{2}$

Total area of all Deserts $=14350000$ sq. $\mathrm{km}$ 

Percentage of Desert in Asia

$=\dfrac{3040000}{14350000} \times 100=21.1 \%$

139. Geography Application: Earth’s total land area is about 148428950 sq. km. The land area of Asia is about 30 percent of this total. What is the approximate land area of Asia to the nearest square km?

Ans: Given, total land area of earth $=148428950k{{m}^{2}}$

Land area of Asia $=30\%$ of land area of earth

$=\dfrac{30}{100}\times 148428950$

$=44528685k{{m}^{2}}$

140. The pieces of Tangrams have been rearranged to make the given shape.

By observing the given shape, answer the following questions: 

• What percentage of total has been coloured? 

(i) Red (R) = _________ 

Ans: Fraction of Red (R) colour

\[\Rightarrow \dfrac{1}{8}+\dfrac{1}{8}+\dfrac{1}{8}=\dfrac{1+1+1}{8}=\dfrac{3}{8}\]

Now, up and down multiply by $100$

$\Rightarrow \dfrac{3}{8}\times \dfrac{100}{100}=\dfrac{300}{8}\%=37.5\%$

Therefore, percentage of red colour $=37.5\%$

(ii) Blue (B) = ________ 

Ans: Fraction for Blue (B) colour 

$\Rightarrow \dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1+1}{4}=\dfrac{2}{4}=\dfrac{1}{2}$

Now, up and down multiply by $100$

$\Rightarrow \dfrac{1}{2}\times \dfrac{100}{100}=\dfrac{100}{2}\%=50\%$

Therefore, percentage of blue colour $=50\%$

(iii) Green (G) = _______ 

Ans: Fraction for Green (G) colour 

$\Rightarrow \dfrac{1}{16}+\dfrac{1}{16}=\dfrac{1+1}{16}=\dfrac{2}{16}=\dfrac{1}{8}$

Now, up and down multiply by $100$

$\Rightarrow \dfrac{1}{8}\times \dfrac{100}{100}=\dfrac{100}{8}\%=12.50\%$

Therefore, percentage of green colour $=12.50\%$

• Check that the sum of all the percentages calculated above should be 100. 

Ans: Now, sum of all percentage 

$=\left( 37.5+50+12.5 \right)\%=100\%$

• If we rearrange the same pieces to form some other shape, will the percentage of colours change? 

Ans: The percentage of colour will not change if we rearrange the same pieces to form another shape.

Importance of mathematics for good grades

Students these days know the importance of getting good grades and excelling in their studies. Although there are various subjects that they have on their plates, there is still a lot of effort that they must put in to make the most of their abilities. In Class 7, it is necessary to get a hold on the subjects of utmost significance like Maths. This subject is linked to most of the science subjects students will study in the higher Classes. The conceptual foundation of this subject decides the career choices students will make and proceed. 

NCERT Exemplar Class 7 Comparing Quantities Solutions - Ideal study material 

Students are encouraged to ensure that they get the most out of the revision or study material out there. That is why the NCERT Exemplar Class 7 Maths Solutions for Chapter 7 - Comparing Quantities is one of the best resources for preparation that students must consider. Students can now achieve great results just by strategizing their study process as per the chapters that are there in their course. 

The students in this 21st century are very well equipped with the best technology as well as the best ways in which they can learn things on the go. It is also worth mentioning that the students can take the help of online platforms such as Vedantu, to get the PDFs for their revisions.   

Considering the different sections of this chapter, you will need a solid foundation regarding clarification of your doubts while solving the problems in the exercises. This is where you will get the best aid from NCERT Exemplar solutions designed by the top experts of Vedantu for Class 7 mathematics. Get this file today and add it to your study material. You will also find the solution files for other chapters to download and for future reference. Prepare the concepts well and define your preparation for the exams.