NCERT Exemplar for Class 11 Physics Chapter 8 - Gravitation (Book Solutions)

Multiple Choice Questions – I

1. The earth is just an approximate sphere. If the interior contained matter which is not of the same density everywhere, then on the surface of the earth, the acceleration due to gravity

(a) Will be focused on the centre but not the same everywhere.

(b) Will have the same value everywhere but not directed towards the centre.

(c) Will be same or constant everywhere in magnitude directed towards the centre.

(d) Cannot be zero at any point.

Ans: Here Correct option is (d)

Because As we know that ${\text{g =}}\dfrac{{\text{4}}}{{\text{3}}}{\text{}\pi{ pGR}}$ , here if density is non-uniform then ${\text{g}}$ will be different on the surface at different point. So, in this equation if we substitute any value of density, we will get ${\text{g}} \ne {\text{0}}$ at any point.

2. As observed from Earth, the sun seems to move in an approximate circular orbit. For the motion of another planet like Mercury as observed from Earth, this would

(a) be equally true.

(b) not be true because the force between Earth and Mercury is not inverse square law.

(c) not be true because the major gravitational force on Mercury is due to Sun.

(d) not be true because Mercury is influenced by forces other than gravitational forces.

Ans: Here Correct option is (c)

Because as we know that gravitational force of attraction between earth and sun always follows inverse square law which is universal law. So, as observed from earth, relative motion between these will not be circular as sun is very large than earth due to relative motion of sun and earth with mercury.

3. Different points in the earth are at slightly different distances from the sun and hence experience different forces owing to gravitation. For a rigid body, we know that if various forces act at various points in it, the resultant motion is as if a net force acts on the c.m. (centre of mass) causing translation and a net torque at the c.m. causing rotation around an axis through the c.m. For the Earth-Sun system (approximating the earth as a uniform density sphere)

(a) the torque is zero.

(b) the torque causes the earth to spin.

(c) the rigid body result does not apply since the earth is not even approximately a rigid body.

(d) the torque causes the earth to move around the sun.

Ans: Here Correct option is (a)

Because due to gravitational attractive force torque on earth is zero as ${\text{F}}$ (denotes force) and ${\text{}\bar{ r}}$ (denotes line joining). So, point of application at centre of mass of earth is along the same direction. Thus, angle between 

${\text{}\bar{ r, }\bar{ F  =  0}}$

$\bar \tau {\text{  =  }\bar{ r }} \times {\text{ }\bar{ F  =  |}\bar{ r||}\bar{ F| sin 0  =  0}}$

4. Satellites orbiting the earth have a finite life and sometimes debris of satellites fall to the earth. This is because

(a) the solar cells and batteries in satellites run out.

(b) the laws of gravitation predict a trajectory spiralling inwards.

(c) of viscous forces causing the speed of satellite and hence height to gradually decrease.

(d) of collisions with other satellites.

Ans: Here Correct option is (c)

Because due to earth with mass ${\text{M}}$, satellite orbiting in orbit with radius ${\text{r}}$ ${\text{ =  }}\dfrac{{{\text{ - GM}}}}{{{\text{2r}}}}$

where negative sign denotes force of attraction between satellite and earth. Due to atmospheric friction, energy if continuously decreasing so radius of orbit or height also decreasing then it comes back to earth with high speed, then burns in atmosphere. 

5. Both earth and moon are subject to the gravitational force of the sun. As observed from the sun, the orbit of the moon

(a) will be elliptical.

(b) will not be strictly elliptical because the total gravitational force on it is not central.

(c) is not elliptical but will necessarily be a closed curve.

(d) deviates considerably from being elliptical due to influence of planets other than earth

Ans: Here Correct option is (b)

Because force which acts on moon is due to gravitational force of attraction between earth and sun whereas moon is not always on joining lines with sun and earth. Thus, two forces which have different lines of action or forces are not central. Hence, motion will not strictly elliptical.

6. In our solar system, the inter-planetary region has chunks of matter (much smaller in size compared to planets) called asteroids. They

(a) will not move around the sun since they have very small masses compared to the sun.

(b) will move along an irregular path because of their small masses and will drift away into outer space.

(c) will move around the sun in closed orbits but not obey Kepler's laws.

(d) will move in orbits like planets and obey Kepler's laws.

Ans: Here correct option is (d)

Because as we know asteroids moves in orbits like planet which follows Kepler’s law as they act upon by central gravitational forces.

7. Choose the wrong option:

(a) Inertial mass is a measure of difficulty of accelerating a body by an external force whereas the gravitational mass is relevant in determining the gravitational force on it by an external mass.

(b) The gravitational mass and inertial mass are the same in an experimental result.

(c) The acceleration due to gravity on earth is the same for all bodies due to the equality of gravitational mass and inertial mass.

(d) Gravitational mass of a particle like a proton depends on the presence of neighbouring heavy objects but the inertial mass does not.

Ans: Here option (d) is wrong because gravitational mass of proton is equal to inertia mass which is independent from presence of neighbouring heavy objects.

8. Particles of masses ${\text{2M, m, M}}$ are respectively at points A, B and C, where distance AB ${\text{ =  }}\dfrac{{\text{1}}}{{\text{2}}}{\text{(BC), m  <  <  M}}$ and at time ${\text{t  =  0}}$ they are all at rest (as shown in the figure). At subsequent times before any collision takes place:

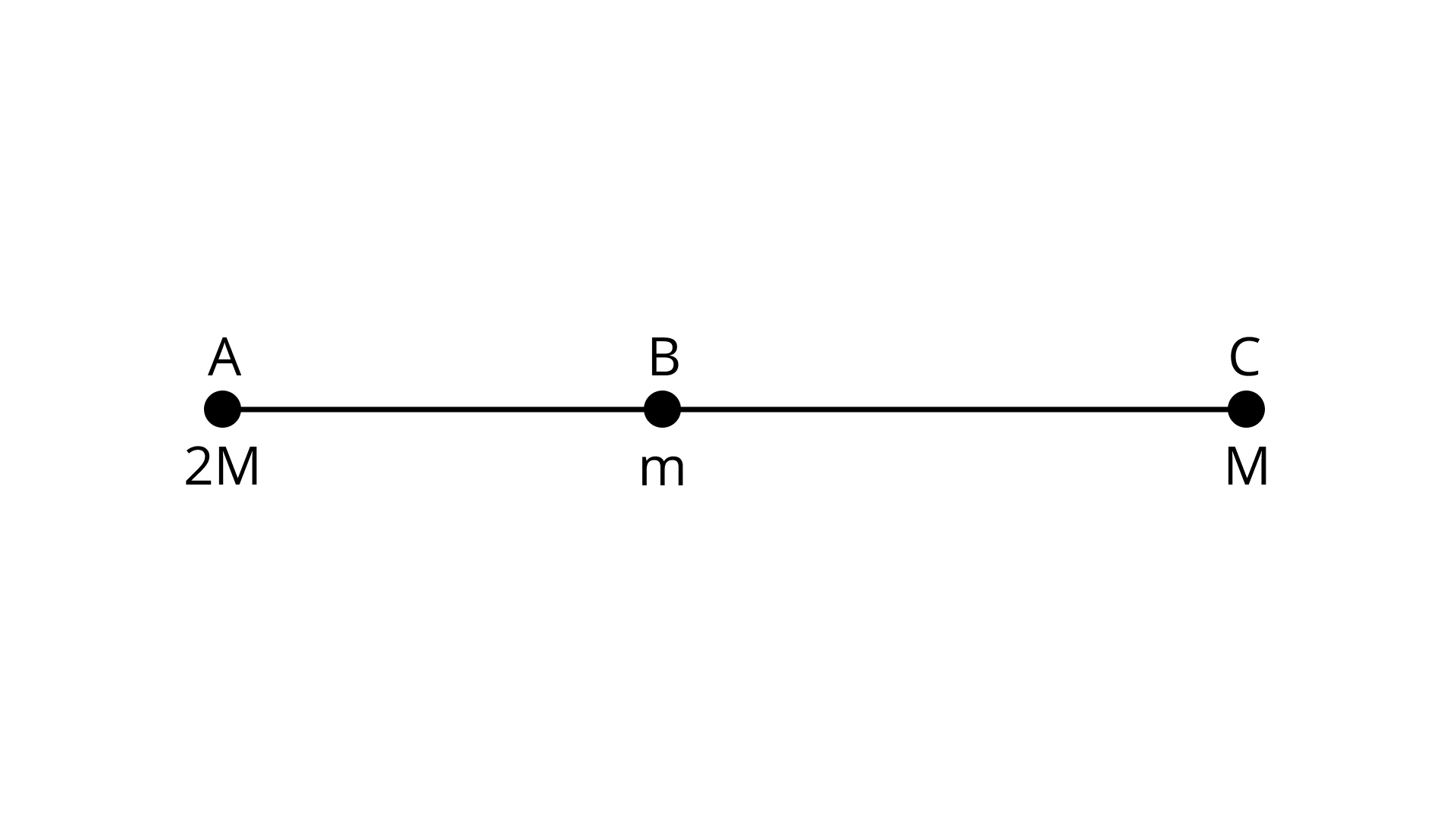
(a) ${\text{m}}$ will remain at rest.

(b) ${\text{m}}$ will move towards ${\text{M}}$

(c) ${\text{m}}$ will move towards ${\text{2M}}$

(d) ${\text{m}}$ will have oscillatory motion.

Ans: Here, correct option is (c) because

Let ${{\text{F}}_{{\text{BC}}}}$ denotes force by mass ${\text{m}}$ at B and due to mass ${\text{M}}$ at C

And FBA denotes force by mass ${\text{m}}$ at B and due to mass ${\text{2M}}$ at A

We get:

${{\text{F}}_{{\text{BC}}}}{\text{  =  G}}\dfrac{{{\text{mM}}}}{{{{{\text{(BC)}}}^{\text{2}}}}}$                                           (i)

${{\text{F}}_{{\text{AB}}}}{\text{  =  G}}\dfrac{{{\text{m2M}}}}{{{{{\text{(BA)}}}^{\text{2}}}}}$                                        (ii)

Assume AB ${\text{ =  x}}$ so, ${\text{x  =  }}\dfrac{{\text{1}}}{{\text{2}}}{\text{BC, BC  =  2x}}$

Put AB and BC in (i) and (ii) we get:

  ${{\text{F}}_{{\text{BC}}}}{\text{  =  G}}\dfrac{{{\text{mM}}}}{{{{{\text{(2x)}}}^{\text{2}}}}}$

  ${{\text{F}}_{{\text{BA}}}}{\text{  =  G}}\dfrac{{{\text{m2M}}}}{{{{{\text{(x)}}}^{\text{2}}}}}$ 

Since ${{\text{F}}_{{\text{BA}}}}{\text{ > }}{{\text{F}}_{{\text{BC}}}}$ . So, ${\text{m}}$ moves towards A.

Multiple Choice Questions – II

9. Which of the following options are correct?

(a) Acceleration due to gravity decreases with increasing altitude.

Ans: Here, acceleration due to gravity at height ${\text{h}}$ is ${{\text{g}}_{\text{h}}}{\text{  =  g}}\left( {{\text{1 - }}\dfrac{{{\text{2h}}}}{{\text{R}}}} \right)$ which implies increasing height decreases value of ${{\text{g}}_{\text{h}}}$ . Hence (a) is correct.

(b) Acceleration due to gravity increases with increasing depth (assume the earth to be a sphere of uniform density).

Ans: Here, acceleration due to gravity at depth ${\text{d}}$ is ${{\text{g}}_{\text{d}}}{\text{  =  g}}\left( {{\text{1 - }}\dfrac{{\text{d}}}{{\text{R}}}} \right)$ which implies increasing depth decreases value of ${{\text{g}}_{\text{d}}}$ . Hence (b) is incorrect.

(c) Acceleration due to gravity increases with increasing latitude.

Ans: Let ${\text{}\lambda{ }}$ be the latitude on earth then ${\text{g}\lambda{   =  g - }}{{\text{}\omega{ }}^{\text{2}}}{\text{Rco}}{{\text{s}}^{\text{2}}}{\text{}\lambda{ }}$

Since value of ${\text{cos}\lambda{ }}$ decreases from ${{\text{0}}^\circ}$ to ${\text{9}}{{\text{0}}^\circ}$ . Thus, due to gravity, acceleration increases from equator $\left( {{\text{}\lambda{   =  }}{{\text{0}}^\circ}} \right)$ to pole $\left( {{\text{}\lambda{   =  9}}{{\text{0}}^\circ}} \right)$ . Hence (c) is correct.

(d) Acceleration due to gravity is independent of the mass of the earth.

Ans: Due to gravity, acceleration on earth surface is ${\text{g  =  }}\dfrac{{{\text{G}}{{\text{M}}_{\text{e}}}}}{{{\text{R}}_{\text{e}}^{\text{2}}}}$ . Thus, It depends on mass of earth. Hence, (d) is incorrect.

10. 8.10. If the law of gravitation, instead of being inverse-square law, becomes an inversecube law:

(a) planets will not have elliptic orbits.

Ans: If law of gravitation becomes inverse cube law as compared to inverse square law. Then for mass planet ${{\text{m}}_{\text{p}}}$ which revolves around sun of mass ${{\text{M}}_{\text{s}}}$ . Thus we get

Force of gravitation ${\text{ = }}$ centrifugal force in circular motion

which implies $\dfrac{{{\text{G}}{{\text{M}}_{\text{s}}}{{\text{m}}_{\text{p}}}}}{{{{\text{r}}^{\text{3}}}}}{\text{  =  }}\dfrac{{{{\text{m}}_{\text{p}}}{\text{v}}_{\text{0}}^{\text{2}}}}{{\text{r}}}$

${\text{v}}_{\text{0}}^{\text{2}}{\text{  =  }}\dfrac{{{\text{G}}{{\text{M}}_{\text{s}}}}}{{{{\text{r}}^{\text{2}}}}}$ where ${\text{r}}$ denotes radius, ${{\text{m}}_{\text{p}}}$ denotes mass of planet, ${{\text{M}}_{\text{S}}}$ denotes mass of sun

So, orbital velocity of planet ${{\text{v}}_{\text{0}}}{\text{  =  }}\dfrac{{\sqrt {{\text{G}}{{\text{M}}_{\text{s}}}} }}{{\text{r}}}{\text{ , }}{{\text{v}}_{\text{0}}} \propto \dfrac{{\text{1}}}{{\text{r}}}$

Time ${\text{ =  }}\dfrac{{{\text{2}\pi{ r}}}}{{{{\text{v}}_{\text{0}}}}}$

${\text{T  =  }}\dfrac{{{\text{2}\pi{ r \times r}}}}{{\sqrt {{\text{G}}{{\text{M}}_{\text{s}}}} }}{\text{  =  }}\dfrac{{{\text{2}\pi{ }}{{\text{r}}^{\text{2}}}}}{{\sqrt {{\text{G}}{{\text{M}}_{\text{s}}}} }}{\text{ }} \Rightarrow {\text{ T}} \propto {{\text{r}}^{\text{2}}}$                                   (i)

or ${{\text{T}}^{\text{2}}} \propto {{\text{r}}^{\text{4}}}$

Thus, by Kepler’s law, eliptical condition is ${{\text{T}}^{\text{2}}} \propto {{\text{r}}^{\text{3}}}$4 . Hence, planetary motion is not elliptical.

Thus, (a) is correct.

(b) circular orbits of planets is not possible.

Ans: Here, circular orbit is not possible. So, by inverse law, we know that $\mathrm{F}=\dfrac{\mathrm{GM}}{\mathrm{r}^{3}} \times \mathrm{m}=\mathrm{mg}$ where ${\text{F}}$ denotes force, ${\text{r}}$ denotes radius, ${\text{M}}$ denotes mass of earth, ${\text{m}}$ denotes mass of stone, ${{\text{g}}^{\text{'}}}$ denotes new acceleration due to gravity

So, path is projectile with parabolic ${\text{T }} \propto {\text{ }}{{\text{r}}^2}$                          [by (i)]

Hence, (b) is incorrect. 

(c) projectile motion of a stone thrown by hand on the surface of the earth will be approximately parabolic.

Ans: This is correct which follows from above two points.

(d) there will be no gravitational force inside a spherical shell of uniform density.

Ans: This is incorrect because gravitational force is universal which acts everywhere.

11. If the mass of sun were ten times smaller and gravitational constant G were ten times larger in magnitudes.

Ans: Let G denotes gravitational constant which is ten times larger in magnitude i.e. $\mathrm{G}^{\prime}=10 \mathrm{G}$

Due to earth, gravitational field is $g^{\prime}=\dfrac{G M_{e}}{r^{2}}=\dfrac{10 G M_{e}}{r^{2}}=10 g$

Weight $=\mathrm{mg}^{\prime}=\mathrm{m} \times 10 \mathrm{~g}=10 \mathrm{mg}$

Force $\quad F=\dfrac{G M_{\mathrm{s}} \mathrm{m}}{r^{2}}$

Mass $\mathrm{M}_{\mathrm{s}}^{\prime}=\dfrac{1}{10} \mathrm{M}_{\mathrm{s}} \Rightarrow 10 \mathrm{M}_{\mathrm{s}}^{\prime}=\mathrm{M}_{\mathrm{s}}$

$\mathrm{F}=\dfrac{\mathrm{GM}_{\mathrm{s}} \mathrm{m}}{10 \mathrm{r}^{2}}$

So, weight becomes ten times larger. Thus, it is difficult to walk.

Hence, option (a) is correct.

(b) the acceleration due to gravity on earth will not change.

Ans: Since from above condition we get $g^{\prime}=10 \mathrm{~g}$, so acceleration changes due to gravity. Hence, (b) is incorrect.

(c) raindrops will fall much faster.

Ans: Here terminal velocity represents as $\mathrm{v}_{\mathrm{T}} \propto \mathrm{g}, \mathrm{g}^{\prime}, \mathrm{g}^{\prime}=10 \mathrm{~g}$ which is also increases ten times. Thus, rain drops fall ten times faster. Hence (c) is correct.

(d) airplanes will have to travel much faster.

Ans: Since we know $g^{\prime}=10 g$ to maintain the gravitational force and speed of aeroplane.

12. If the sun and the planets carried huge amounts of opposite charges,

(a) all three of Kepler's laws would still be valid.

(b) only the third law will be valid.

(c) the second law will not change.

(d) the first law will still be valid.

Ans: Here option (a, c, d) is correct because of same reason i.e. Along with gravitational force, attractive electrostatic forces of attraction produces large where both forces are added and radial in nature. As they are central forces and follows inverse square law. Hence, all three Kepler’s law will be valid.

13. There have been suggestions that the value of the gravitational constant ${\text{G}}$ becomes smaller when considered over very large time period (in billions of years) in the future. If that happens, for our earth,

(a) nothing will change.

(b) we will become hotter after billions of years.

(c) we will be going around but not strictly in closed orbits.

(d) after sufficiently long time we will leave the solar system.

Ans: Here option $(c, d)$ is correct and $(a, b)$ is incorrect, because

As we know that centripetal force followed by gravitational force $\mathrm{F}_{\mathrm{g}}=\dfrac{\mathrm{GM}_{\mathrm{s}} \mathrm{m}_{\mathrm{c}}}{\mathrm{r}^{2}}$

Now, accordingly from question, if $\mathrm{G}$ becomes smaller then it reduces centripetal force.

So, orbital velocity $\mathrm{v}_{0}=\sqrt{\dfrac{\mathrm{GM}_{\mathrm{s}}}{\mathrm{r}}}, \mathrm{v} \propto \sqrt{\mathrm{G}}$ is decreases to small value which implies centrifugal force is larger as compared to centripetal force i.e. $\mathrm{F}_{\mathrm{g}} \propto \mathrm{G}$. Thus, earth moved in larger orbit, so distance from earth is increased and temperature drops down and orbit will not be closed one.

14. Supposing Newton's law of gravitation for gravitation forces $\overline{\mathrm{F}}_{1}, \overline{\mathrm{F}}_{2}$ between two masses $\mathrm{m}_{1}, \mathrm{~m}_{2}$ at positions $\overrightarrow{\mathrm{r}_{1}}, \overrightarrow{\mathrm{r}_{2}}$ read $\overrightarrow{\mathrm{F}_{1}}=-\overrightarrow{\mathrm{F}_{2}}=-\dfrac{\overrightarrow{\mathrm{r}_{12}}}{\mathrm{r}_{12}^{3}} \mathrm{GM}_{0}^{2}\left[\dfrac{\mathrm{m}_{1} \mathrm{~m}_{2}}{\mathrm{M}_{0}^{2}}\right]$ where $\mathrm{M}_{0}$ is a constant of dimension of mass, $\overrightarrow{r_{12}}=\overrightarrow{r_{1}}-\overrightarrow{r_{2}}$ and $\mathrm{n}$ is number. In such a case (a)the acceleration due to gravity on earth will be different for different objects.

Ans: As $\overrightarrow{\mathrm{F}_{1}}=-\overrightarrow{\mathrm{F}_{2}}=-\dfrac{\overrightarrow{\mathrm{r}_{12}}}{\mathrm{r}_{12}^{3}} \mathrm{GM}_{0}^{2}\left[\dfrac{\mathrm{m}_{1} \mathrm{~m}_{2}}{\mathrm{M}_{0}^{2}}\right]^{\mathrm{n}}$ given $\overrightarrow{\mathrm{r}_{12}}=\overrightarrow{\mathrm{r}_{1}}-\overrightarrow{\mathrm{r}_{2}}$

Acceleration $\mathrm{g}=\dfrac{|\mathrm{F}|}{\operatorname{mass}(\mathrm{m})}$

implies $\mathrm{g}=\left|\dfrac{\mathrm{GM}_{0}^{2}\left(\mathrm{~m}_{1} \mathrm{~m}_{2}\right)^{\mathrm{n}}}{\mathrm{r}_{12}^{3}\left(\mathrm{M}_{0}\right)^{2 \mathrm{n}}} \times \dfrac{\hat{\mathrm{r}}_{12}}{\mathrm{~m}}\right|$ $\mathrm{g}=\dfrac{\mathrm{GM}_{0}^{2}\left(\mathrm{~m}_{1} \mathrm{~m}_{2}\right)^{\mathrm{n}}}{\mathrm{r}_{12}^{2}\left(\mathrm{M}_{0}\right)^{2 \mathrm{n}}} \dfrac{1}{\mathrm{n}}$

and $\hat{r}_{12}$ gives direction of $g$ from one to two. Therefore,

As $\mathrm{g}$ depends on $\left|\mathrm{r}_{12}\right|$, thus $\mathrm{g}$ is different for different bodies of different mass and position. Hence, (a) is correct.

(b) none of the three laws of Kepler will be valid.

Ans: According to part (a), since force is central in nature. Thus, Kepler’s first and second law rejects it. Hence (b) is incorrect.

(c) only the third law will become invalid.

Ans: According to part (a), Since, gravitational force ${\text{g}}$ is not constant. So, Kepler’s third law is not valid. Hence, (c) is correct.

(d) for $\mathrm{n}$ negative, an object lighter than water will sink in water.

Ans: From given condition i.e. for $\mathrm{n}$ negative, we get:

$\mathrm{g}=\dfrac{\mathrm{GM}_{0}^{2}\left(\mathrm{~m}_{1} \mathrm{~m}_{2}\right)^{-\mathrm{n}}}{\left(\mathrm{r}_{12}\right)^{2}\left(\mathrm{M}_{0}\right)^{-2 \mathrm{n}}} \times \dfrac{1}{\mathrm{~m}}$

$\mathrm{~g}=\dfrac{\mathrm{GM}_{0}^{2}\left(\mathrm{~m}_{1} \mathrm{~m}_{2}\right)^{-\mathrm{n}}}{\mathrm{r}_{12}^{2} \mathrm{~m}}=\dfrac{\mathrm{GM}_{0}^{2}}{\left(\mathrm{~m}_{1} \mathrm{~m}_{2}\right)^{\mathrm{n}}} \dfrac{\mathrm{M}_{0}^{2 \mathrm{n}}}{\mathrm{r}_{12}^{2}} \times \dfrac{1}{\mathrm{~m}}$

$\mathrm{~g}=\dfrac{\mathrm{GM}_{0}^{2}}{\mathrm{r}_{12}^{2}}\left[\dfrac{\mathrm{M}_{0}^{2}}{\mathrm{~m}_{1} \mathrm{~m}_{2}}\right]^{\mathrm{n}} \times \dfrac{1}{\mathrm{~m}}$

$\because \mathrm{g}>0$

$\Rightarrow \mathrm{M}_{0}>\mathrm{m}_{1}, \mathrm{~m}_{2}$

Thus, this case implies lighter object sink in water, Hence (d) is correct.

15. Which of the following are true?

(a) A polar satellite goes around the earth's pole in north-south direction.

(b) A geostationary satellite goes around the earth in east-west direction.

(c) A geostationary satellite goes around the earth in west-east direction.

(d) A polar satellite goes around the earth in east-west direction.

Ans: Here, option (a, c) are correct because as we know that the satellite which appears as stationary relative to earth is known as geostationary satellite which revolves around earth in west-east direction with angular velocity same as earth around its own axis. So, A polar satellite revolving in north-south direction around pole of the earth and its is independent on earth’s rotation. 

16. The centre of mass of an extended body on the surface of the earth and its centre of gravity

(a) are always at the same point for any size of the body.

(b) are always at the same point only for spherical bodies.

(c) can never be at the same point.

(d) is close to each other for objects, say of sizes less than ${\text{100 m}}$

(e) both can change if the object is taken deep inside the earth

Ans: Here, the correct option is (d) because

Centre of gravity depends on the weight of body whereas centre of mass depends on mass of body. We denotes centre of gravity as COG whereas centre of mass as COM. So, COG is a point in body which balanced the body perfectly. Net torque at COG is zero whereas COM is average location of mass distribution where whole mass is concentrated. If we have given some angular momentum so body spin arount COM. For small body, assume size which is less than ${\text{100 m}}$ , ${\text{ <  < }}{{\text{R}}_{\text{s}}}$ , which is placed in uniform gravitational field, COM is close to COG. If body size increases so weight changes and COM, COG become far from each other. Since suppose in spherical ball where COM and COG are same but similarly in case of mountain, COM and COG are not aligned and COM lie bit above COG. Hence, (d) is correct.

Very Short Answer Type Questions

17. Molecules in the air in the atmosphere are attracted by gravitational force of the earth. Explain why all of them do not fall into the earth just like an apple falling from a tree.

Ans: Air molecules and apples both are attracted by gravitational force but velocity of air molecules is not same downward as apple (since apple has no other direction except downwad) as air molecules randomly possess thermal or temperature energy. 

18. Give two example each of a central force and a non-central force

Ans: Example of central force is gravitational force, electrostatic force which point mass and charges whereas Example of non-central force is spin dependent nuclear force, magnetic force between two current loops.

19. Draw areal velocity versus time graph for mars.

Ans: Here mars is planet which follows Kepler’s law. So, according to Kepler’s second law, areal velocity by position vector of planet from sun to planet is always constant. Here is the graph which shows areal velocity time graph for mars:

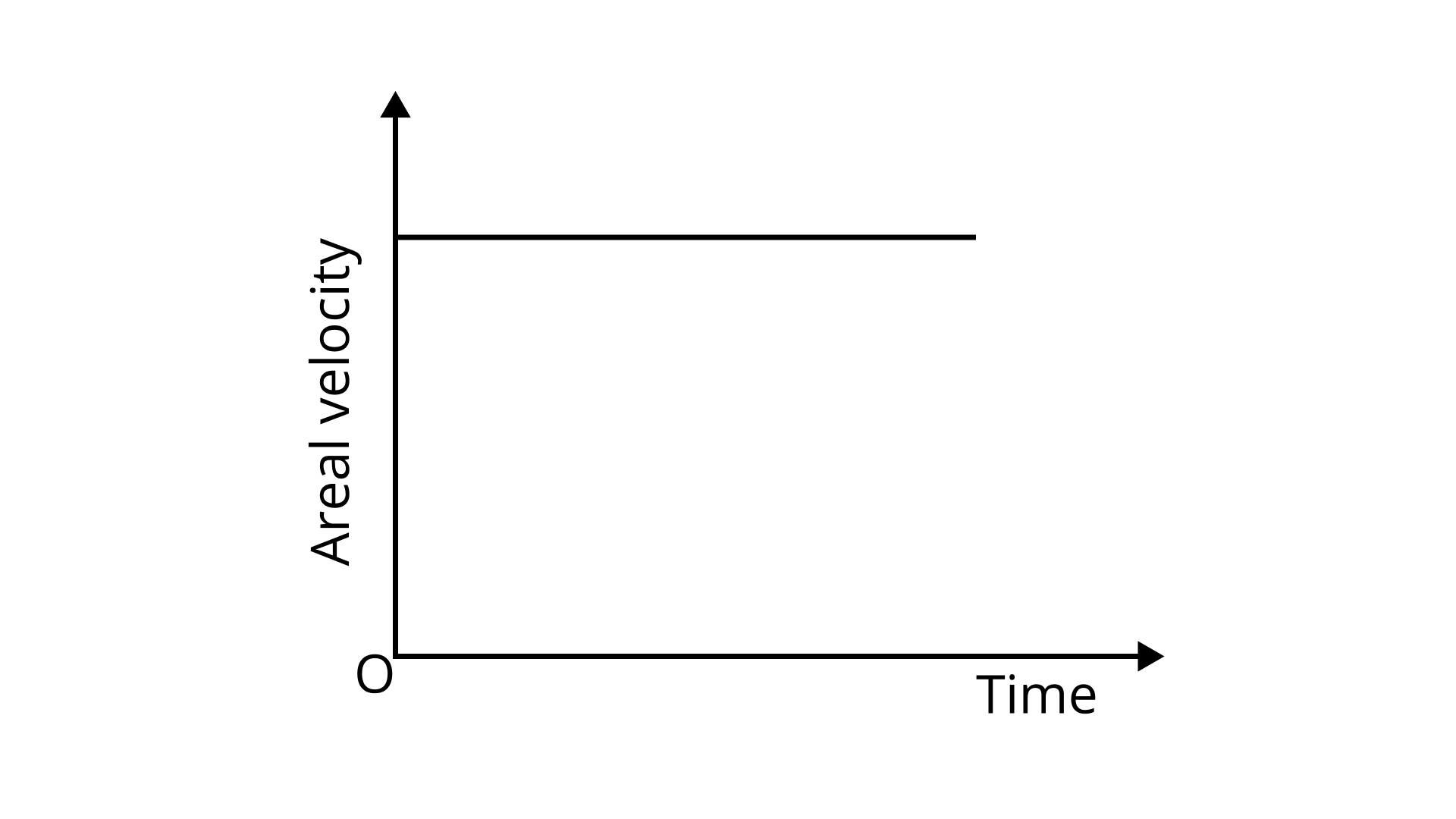
20. What is the direction of areal velocity of the earth around the sun?

Ans: Here areal velocity of earth around sun $\dfrac{{{\text{dA}}}}{{{\text{dt}}}}{\text{  =  }}\dfrac{{\text{L}}}{{{\text{2m}}}}$ 

where ${\text{L}}$ represents angular momentum

and ${\text{m}}$ represents mass of earth

But ${\text{L  =  }\vec r{ \times }\vec p{  =  \vec r \times m\vec v}}$

Thus, $\dfrac{{{\text{dA}}}}{{{\text{dt}}}}{\text{  =  }}\dfrac{{\text{1}}}{{{\text{2m}}}}{\text{(}\vec r{ \times m}\vec v{)  =  }}\dfrac{{\text{1}}}{{\text{2}}}{\text{}\vec r{ \times \vec v}}$

So, direction of areal velocity is perpendicular to plane ${\text{}\vec r{, }\vec v{}}$ which is according to RHG (right hand grip) rule of Maxwell

21. How is the gravitational force between two points masses affected when they are dipped in water keeping the separation between them the same?

Ans: As we know that Newton Universal law of Gravitational force of attraction ${\text{F}}$ between masses ${{\text{m}}_{\text{1}}}{\text{, }}{{\text{m}}_{\text{2}}}$ . distance ${\text{r}}$ is ${\text{F  =  }}\dfrac{{{\text{G}}{{\text{m}}_{\text{1}}}{{\text{m}}_{\text{2}}}}}{{{{\text{r}}^{\text{2}}}}}$

So, ${\text{G}}$ not depend on medium. Thus, force of attraction doesn’t change if masses are in water or in any other medium. 

22. Is it possible for a body to have inertia but no weight?

Ans: As we know each body has mass or inertia. So, weight is measured by spring balance or weighing machine which is equal to ${\text{mg, g}}$ which can be zero or weight of falling body is zero. Now, at centre of earth ${\text{g  =  0}}$ . Thus, weight which is in ${\text{mg}}$ can be zero but mass ${\text{m}}$ never be zero. Hence, it implies inertia is never zero.

23. We can shield a charge from electric fields by putting it inside a hollow conductor. Can we shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?

Ans: Here gravitational force not depends on nature whereas electric force depends on the intervening medium between charge and electric field. Thus, we cannot shield a body from gravitational influence by putting it inside a hollow sphere.

24. An astronaut inside a small spaceship orbiting around the earth cannot detect gravity. If the space station orbiting around the earth has a large size, can he hope to detect gravity?

Ans: Astronaut inside a small spaceship around the earth orbiting very small negligible constant acceleration or we can say value of acceleration supposed to be constant inside a small spaceship and then feel weightlessness. If space station orbiting around the earth has larger in size then astronaut only experience acceleration due to gravity on the moon or on the moon. 

25. The gravitational force between a hollow spherical shell (of radius ${\text{R}}$ and uniform density) and a point mass is ${\text{F}}$ . Show the nature of ${\text{F}}$ versus ${\text{r}}$ graph where ${\text{r}}$ is the distance of the point from the centre of the hollow spherical shell of uniform density.

Ans: Here gravitational force is zero, inside and at the centre of hollow spherical shell and on surface it is denoted as ${{\text{F}}_{\text{o}}}$

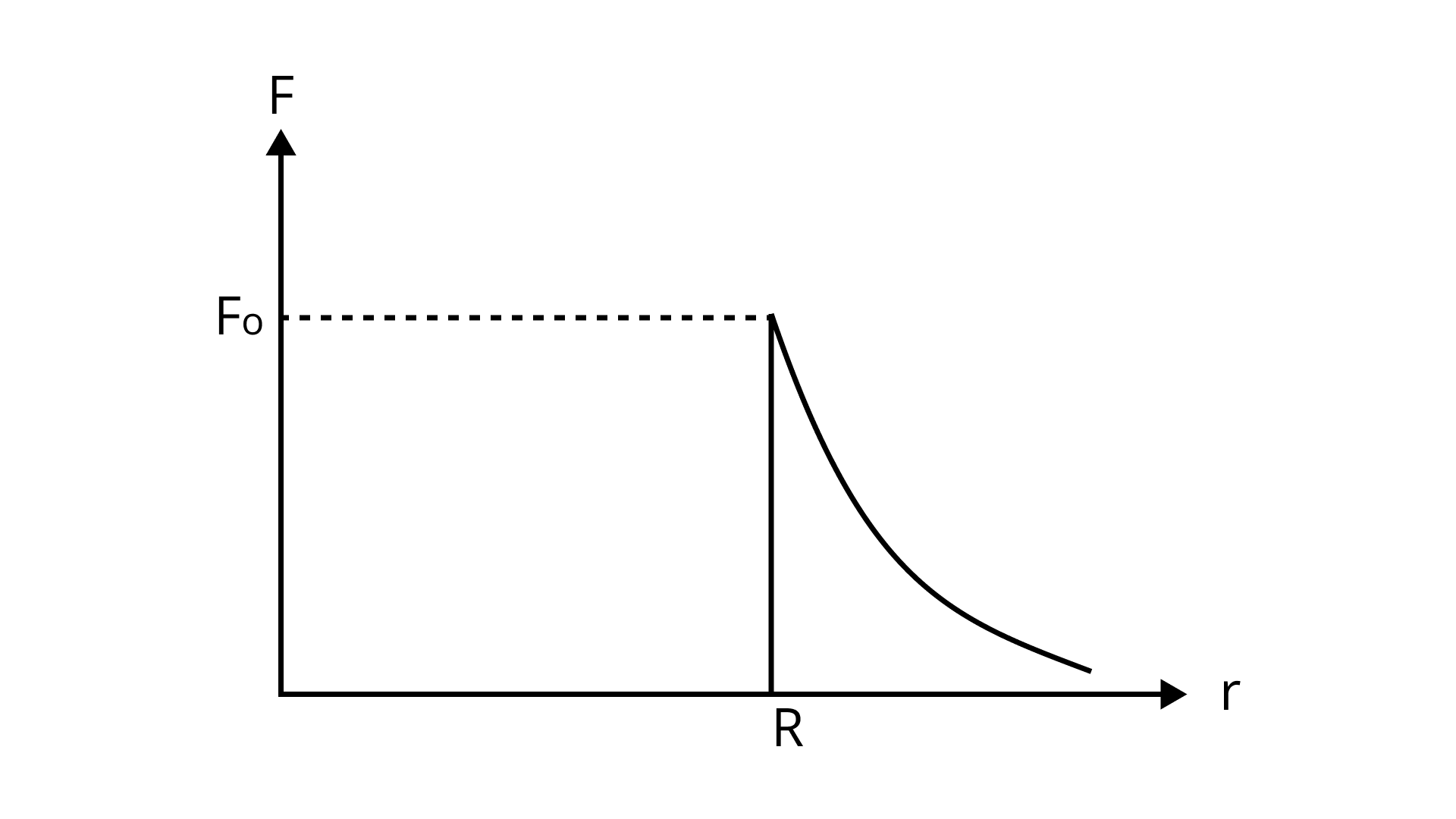
So, gravitational force between hollow shell and mass is ${{\text{F}}_{\text{o}}}{\text{  =  }}\dfrac{{{\text{GMm}}}}{{{{\text{r}}^{\text{2}}}}}$ where ${\text{M}}$ denotes mass of hollow spherical shell and ${\text{m}}$ denotes point mass, ${\text{r}}$ denotes distance between point mass and centre. Thus, mass is distributed on surface then ${{\text{F}}_{\text{o}}}{\text{  =  0}}$ or ${\text{0 < r < R}}$ where ${\text{R}}$ denotes distance from centre to surface.

${{\text{F}}_{\text{o}}}{\text{  =  }}\dfrac{{{\text{GM}}}}{{{{\text{r}}^{\text{2}}}}}$ for ${\text{r >  > R}}$

Thus, changes in ${\text{F}}$ as compared to ${\text{r}}$ is shown in above figure. Hence, if ${\text{r}}$ tends to zero then force is maximum.

26. Out of aphelion and perihelion, where is the speed of the earth more and why?

Ans: 

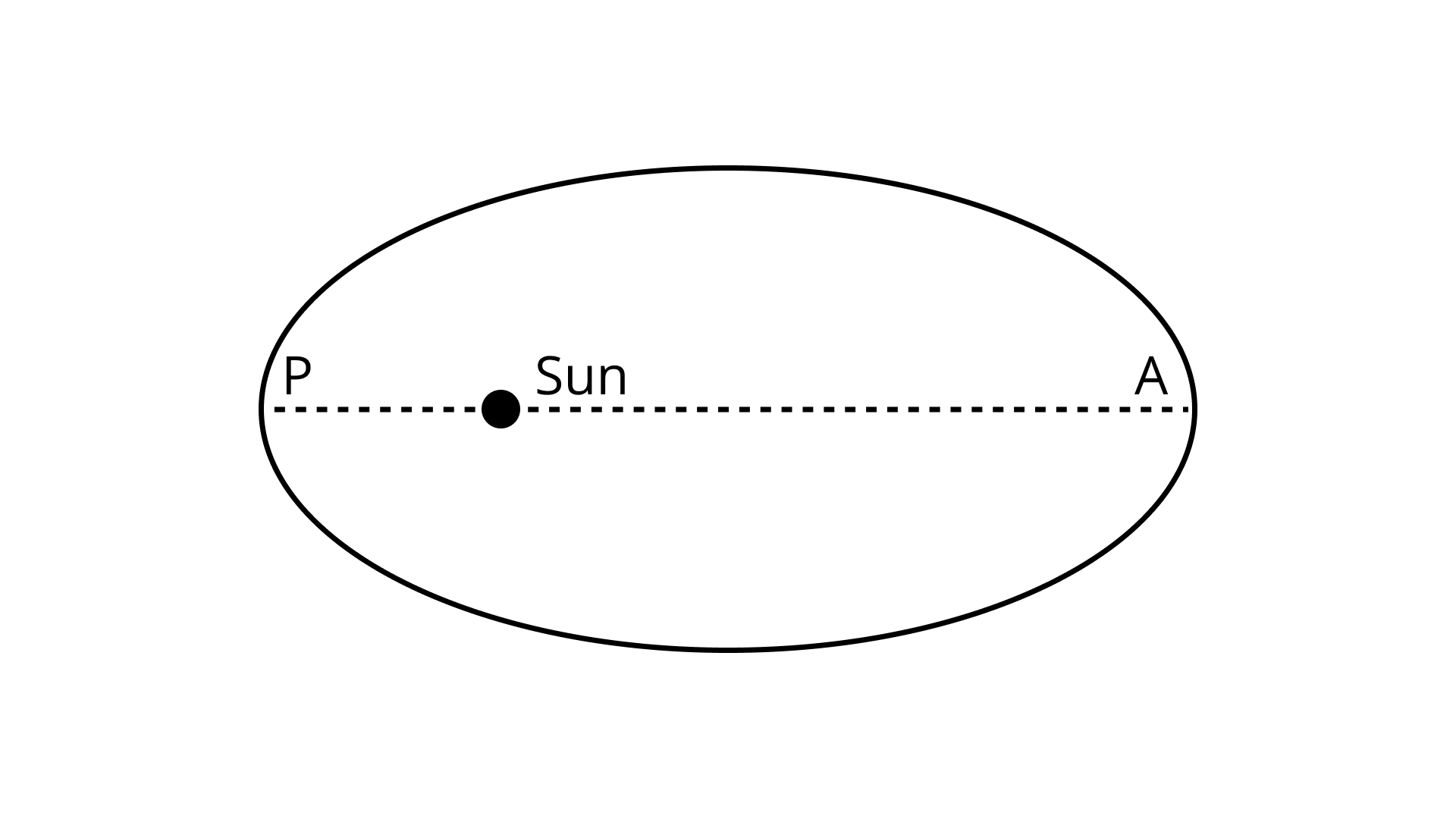
As we know earth revolves around sun in an eliptical orbit. Here, position of earth at P and A at the shortest and longest distance is known as perihelion and aphelion respectively.

Now, from Kepler’s second law, areal velocity around sun is constant which implies 

$\dfrac{{{\text{dA}}}}{{{\text{dt}}}}{\text{  =  }}\dfrac{{\text{L}}}{{{\text{2m}}}}{\text{  =  }}\dfrac{{{\text{r }\times{ p}}}}{{{\text{2m}}}}{\text{  =  }}\dfrac{{{\text{r }\times{ mv}}}}{{{\text{2m}}}}{\text{  =  }}\dfrac{{\text{1}}}{{\text{2}}}{\text{r }\times{ v}}$

Thus, at point P, if ${\text{r}}$ increases at aphelion then ${\text{v}}$decreases whereas if $v$ increases at aphelion then ${\text{r}}$ decreases.

27. What is the angle between the equatorial plane and the orbital plane of:

(a) Polar satellite

Ans: As we know polar satellite revolves from north to south pole. Thus, it makes ${\text{9}}{{\text{0}}^\circ }$ angle with equatorial plane. 

(b) Geostationary satellite

Ans: As we know geostationary satellite revolves from west to east direction with equatorial plane. So, angle between geostationary and equatorial plane is equal to zero.

Short Answer Type Questions

28. Mean solar day is the time interval between two successive noon when the sun passes through the zenith point (meridian). The sidereal day is the time interval between two successive transit of a distant star through the zenith point (meridian).

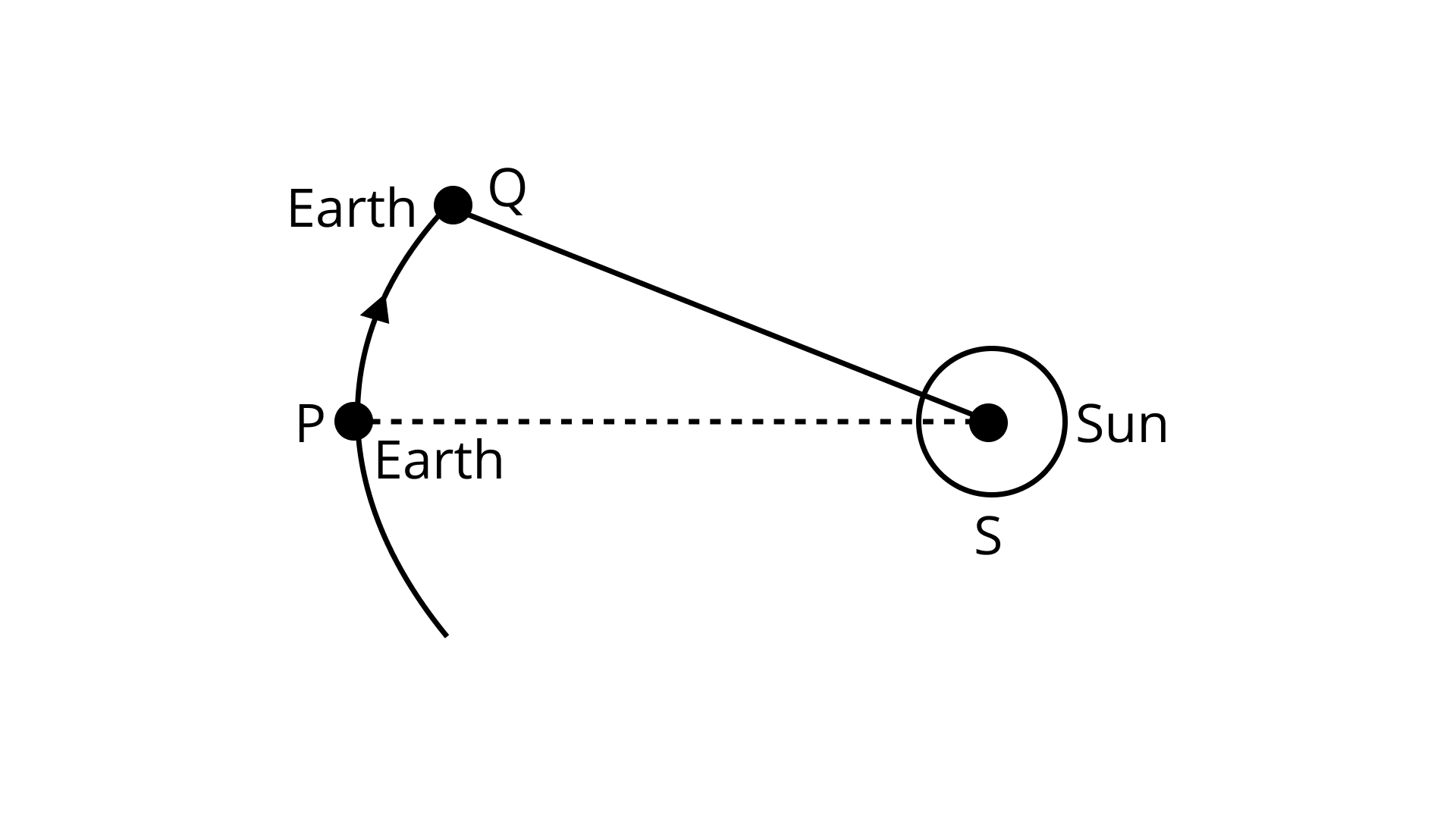
In drawing appropriate diagram showing earth's spin and orbital motion, show that the mean solar day is four minutes longer than the sidereal day. In other words, distant stars would rise four minutes early every successive day. [Hint: you may assume a circular orbit for the earth.]

Ans: Let on noon, sun passes through zenith (meridian). As one revolution is equal to ${\text{36}}{{\text{0}}^\circ}$ . So, After one revolution of earth, sun again passes through zenith. At that time, when earth revolves on its own axis by ${\text{36}}{{\text{0}}^\circ}$ , it changes its $\angle {\text{PSQ  =  }}{{\text{1}}^\circ }$ 

Thus, one solar day represents ${\text{36}}{{\text{1}}^\circ }$ rotation by earth

Now, if ${\text{36}}{{\text{1}}^\circ }$ corresponds to ${\text{24 hr}}$ , this implies ${{\text{1}}^{\text{o}}}{\text{  =  }}\dfrac{{{\text{24}}}}{{{\text{361}}}}{\text{hrs  =  }}\dfrac{{{\text{24}}}}{{{\text{361}}}}{\text{ }\times{ 3600 sec  =  }}3min 59 sec  \approx {\text{ 4min}}$

Hence done.

29. Two identical heavy spheres are separated by a distance $10$ times their radius. Will an object placed at the mid-point of the line joining their centres be in stable equilibrium or unstable equilibrium? Give reason for your answer.

Ans: Let ${\text{m}}$  denotes a point which is placed at midpoint P of line which join centre A, B of sphere

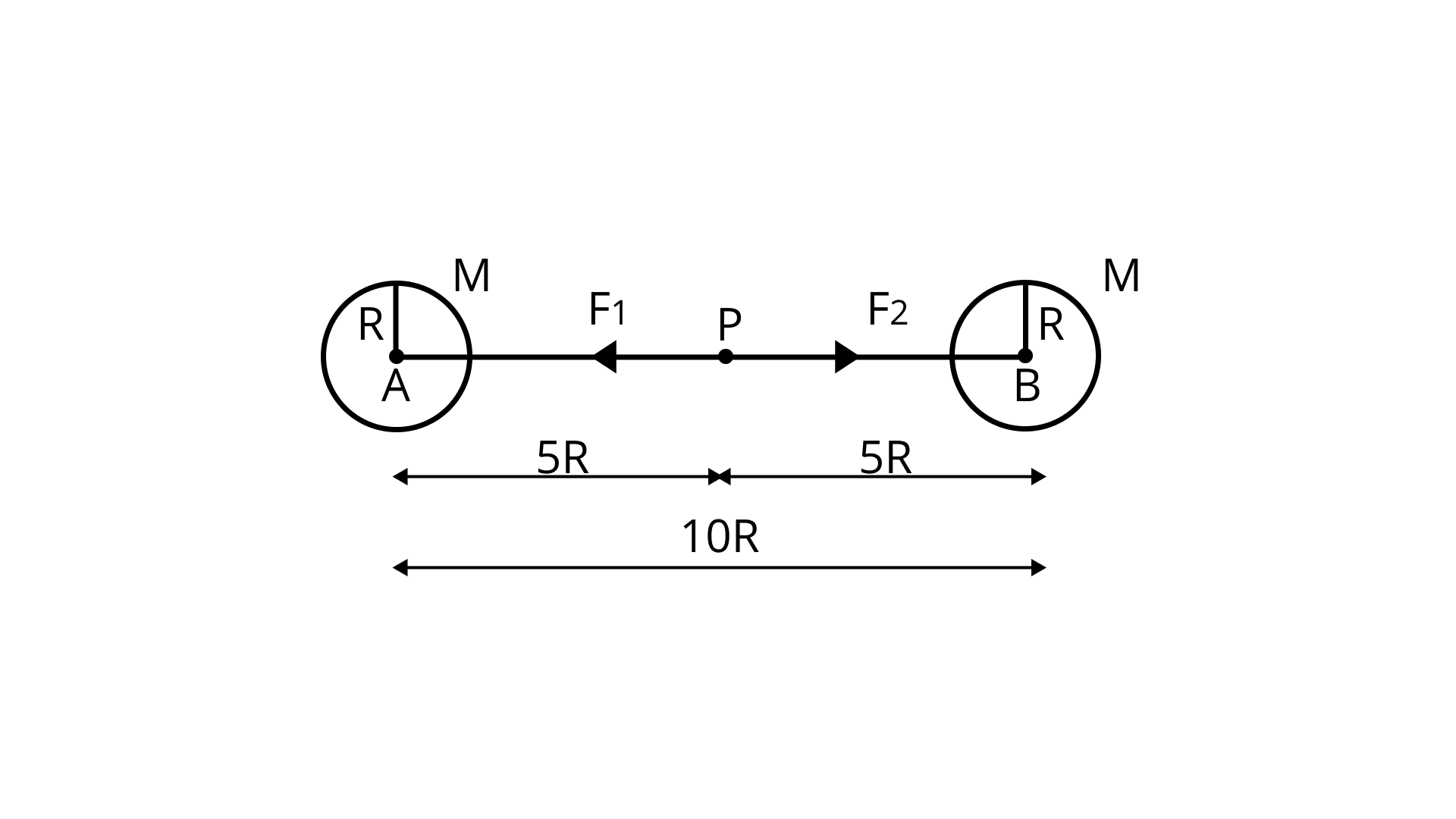
Assume ${{\text{m}}_{\text{1}}}{\text{  =  }}{{\text{m}}_{\text{2}}}{\text{  =  M, r  =  10R}}$

  $\left| {{{\text{F}}_{\text{2}}}} \right|{\text{  =  }}\left| {{{\text{F}}_{\text{1}}}} \right|{\text{  =  }}\dfrac{{{\text{GMm}}}}{{{{{\text{(5R)}}}^{\text{2}}}}}$

  $\left| {{{\text{F}}_{\text{1}}}} \right|{\text{  =  }}\left| {{{\text{F}}_{\text{2}}}} \right|{\text{  =  }}\dfrac{{{\text{GMm}}}}{{{\text{25}}{{\text{R}}^{\text{2}}}}}$ 

Let two forces be ${{\text{F}}_{\text{1}}}{\text{, }}{{\text{F}}_{\text{2}}}$ respectively. As direction of force is opposite, so net force ${{\text{F}}_{\text{1}}}{\text{ + }}{{\text{F}}_{\text{2}}}{\text{  =  0, }}\left( {{{\text{F}}_{\text{1}}}{\text{  =   - }}{{\text{F}}_{\text{2}}}} \right){\text{.m}}$ will be in equilibrium state.

Now, if ${\text{m}}$ is displaced by ${\text{x}}$ from P to A then PA ${\text{ =  (5R - x)}}$ and PB ${\text{ =  (5R + x)}}$

  ${{\text{F}}_{\text{1}}}{\text{  =  }}\dfrac{{{\text{GMm}}}}{{{{{\text{(5R - x)}}}^{\text{2}}}}}{\text{ , }}{{\text{F}}_{\text{2}}}{\text{  =  }}\dfrac{{{\text{GMm}}}}{{{{{\text{(5R + x)}}}^{\text{2}}}}}$

   $\Rightarrow {\text{ }}{{\text{F}}_{\text{2}}}{\text{ < }}{{\text{F}}_{\text{1}}}$ 

Thus, resulting force on P is an unstable equilibrium.

30. Show the nature of the following graph for a satellite orbiting the earth

(a) K.E. versus orbital radius ${\text{R}}$

Ans: Let mass of earth be ${{\text{M}}_{\text{e}}}$

Radius be ${\text{R}}$

Mass of satellite be ${\text{m}}$

So, orbital velocity ${{\text{v}}_{\text{0}}}{\text{  =  }}\sqrt {\dfrac{{{\text{GM}}}}{{\text{R}}}}$

Now, ${{\text{E}}_{\text{K}}}$ versus ${\text{R}}$

${\text{K}}{{\text{E}}_{\text{k}}}{\text{  =  }}\dfrac{{\text{1}}}{{\text{2}}}{\text{mv}}_{\text{0}}^{\text{2}}{\text{  =  }}\dfrac{{\text{1}}}{{\text{2}}}{\text{m }\times{ }}\dfrac{{{\text{GM}}}}{{\text{R}}}{\text{  =  }}\dfrac{{{\text{GMm}}}}{{{\text{2R}}}}$

${{\text{E}}_{\text{k}}} \propto \dfrac{{\text{1}}}{{\text{R}}}$

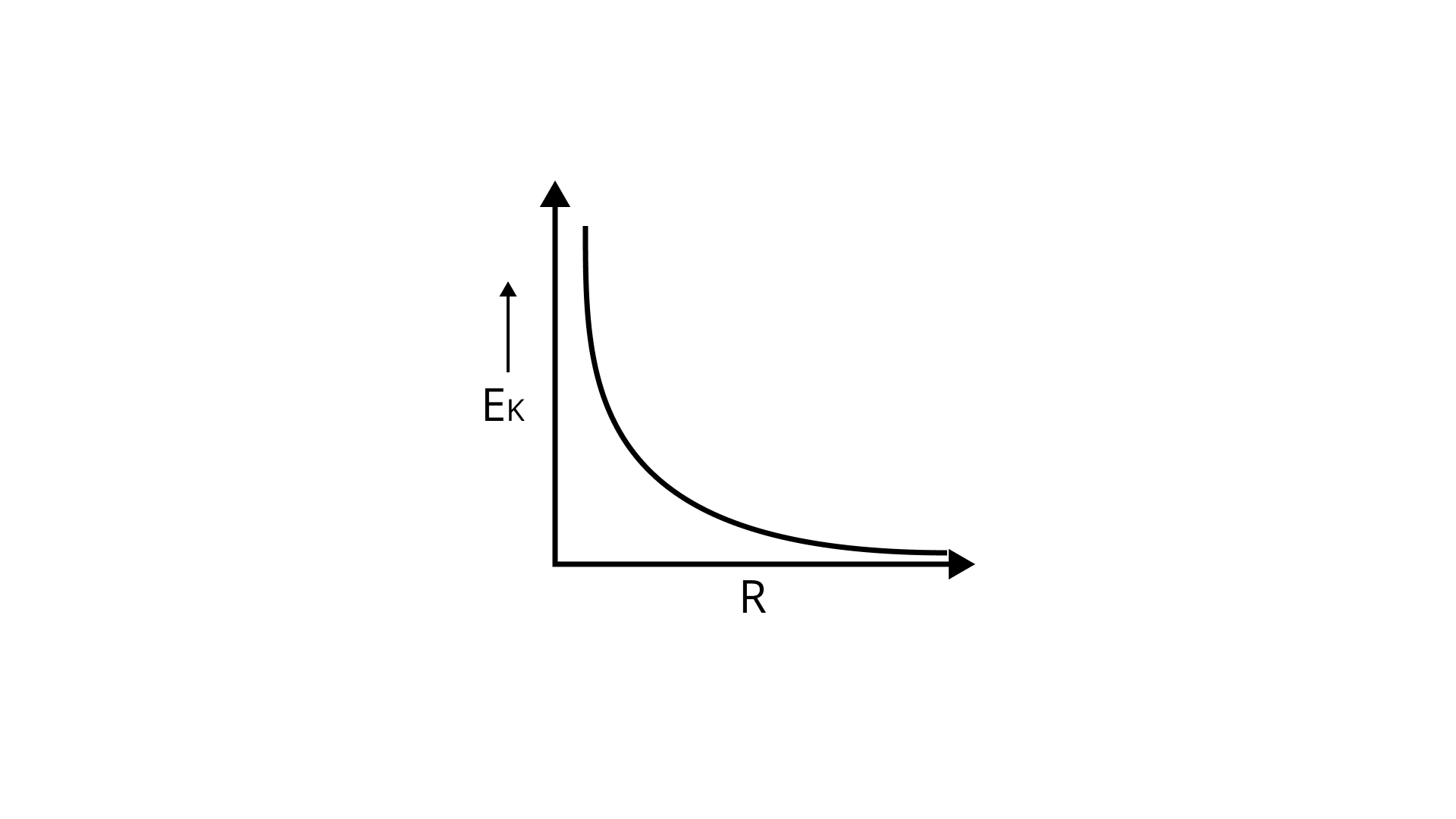
Hence, ${{\text{E}}_{\text{k}}}$ decreases with ${\text{R}}$

(b) P.E. versus orbital radius ${\text{R}}$

Ans: ${{\text{E}}_{\text{p}}}$ versus ${\text{R}}$

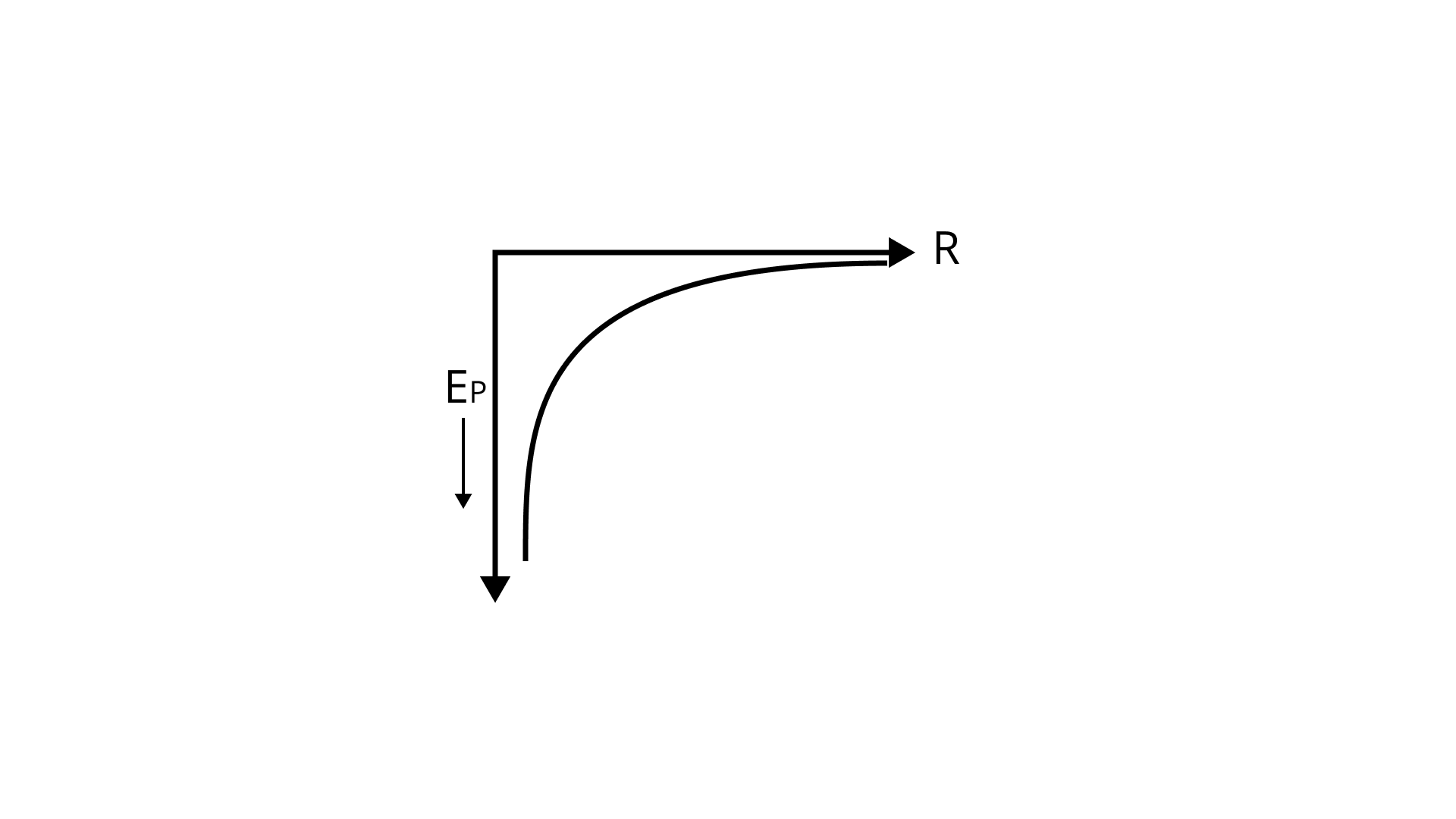
  ${{\text{E}}_{\text{p}}}{\text{  =  }}\dfrac{{{\text{ - GMm}}}}{{\text{R}}}$

  ${{\text{E}}_{\text{p}}} \propto {\text{ - }}\dfrac{{\text{1}}}{{\text{R}}}$ 

(c) T.E. versus orbital radius ${\text{R}}$

Ans: T.E. versus ${\text{R}}$

 ${{\text{E}}_{\text{k}}}{\text{  =   + }}\dfrac{{\text{1}}}{{\text{2}}}\dfrac{{{\text{GMm}}}}{{\text{R}}}$

 ${{\text{E}}_{\text{p}}}{\text{  =  }}\dfrac{{{\text{ - GMm}}}}{{\text{R}}}$

  ${\text{T}}{\text{.E}}{\text{.  =  E  =  }}\dfrac{{\text{1}}}{{\text{2}}}\dfrac{{{\text{GMm}}}}{{\text{R}}}{\text{ - }}\dfrac{{{\text{GMm}}}}{{\text{R}}}$

  ${\text{E  =  }}\dfrac{{{\text{ - 1}}}}{{\text{2}}}\dfrac{{{\text{GMm}}}}{{\text{R}}}$ 

31. Shown are several curves (figure). Explain with reason, which one amongst them can be a possible trajectory traced by a projectile (neglect air friction).

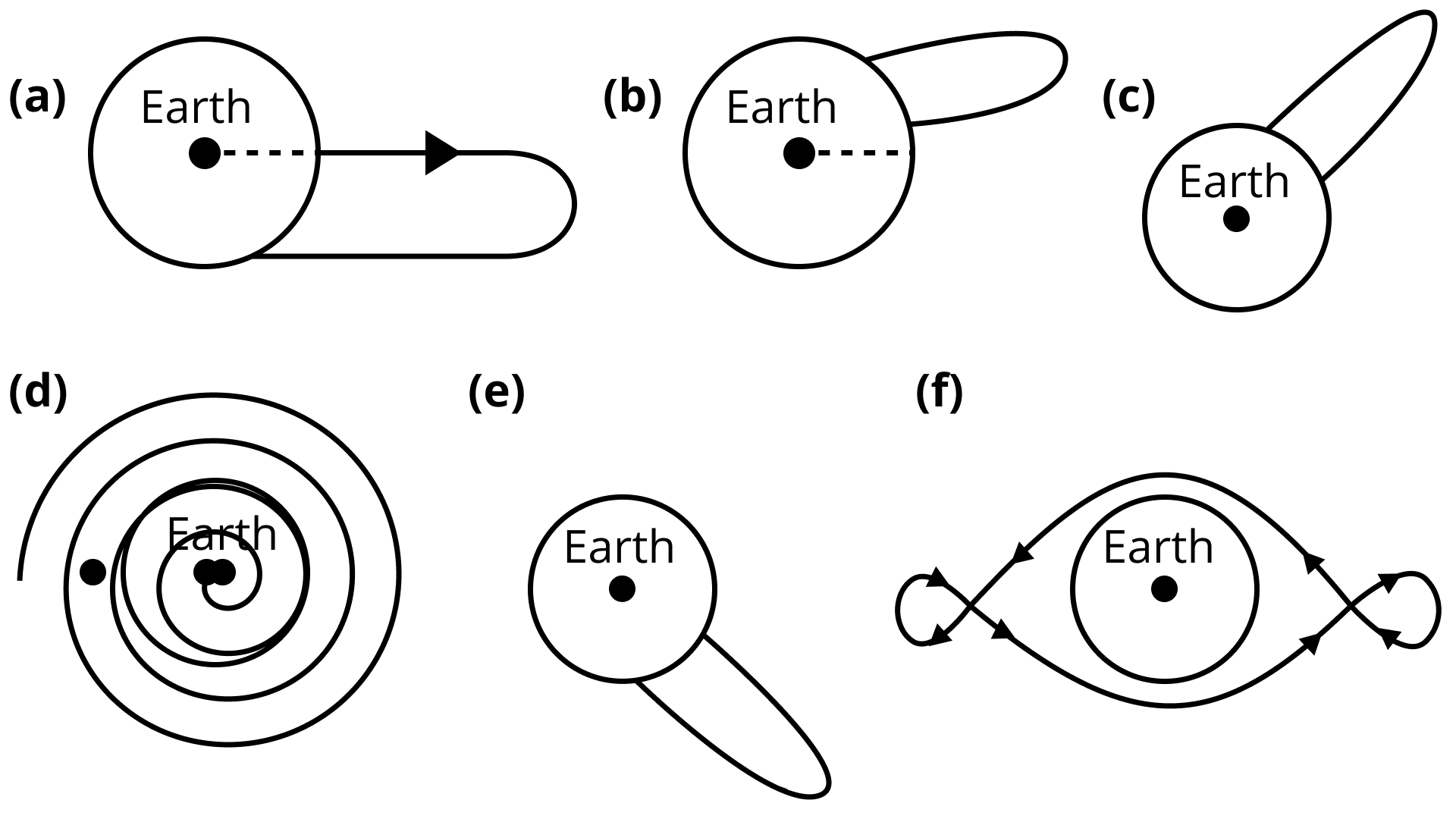
Ans: Here, trajectory of path which is followed by projectile under gravitational force of earth will be conic section or parabolic or elliptical or focus must be with centre. So, accordingly, only option (c) is required which shows centre of earth as focus of trajectory.

32. An object of mass ${\text{m}}$ is raised from the surface of the earth to a height equal to the radius of the earth, it is taken from a distance ${\text{R}}$ to ${\text{2R}}$ from the centre of the earth. What is the gain in its potential energy?

Ans: Since mass ${\text{m}}$ is lifted upward from surface to height which is equal to earth i.e. from ${\text{R}} \to {\text{2R}}$

So, (P.E.) potential energy of body on the surface of earth be $\dfrac{{{\text{ - GMm}}}}{{\text{R}}}$

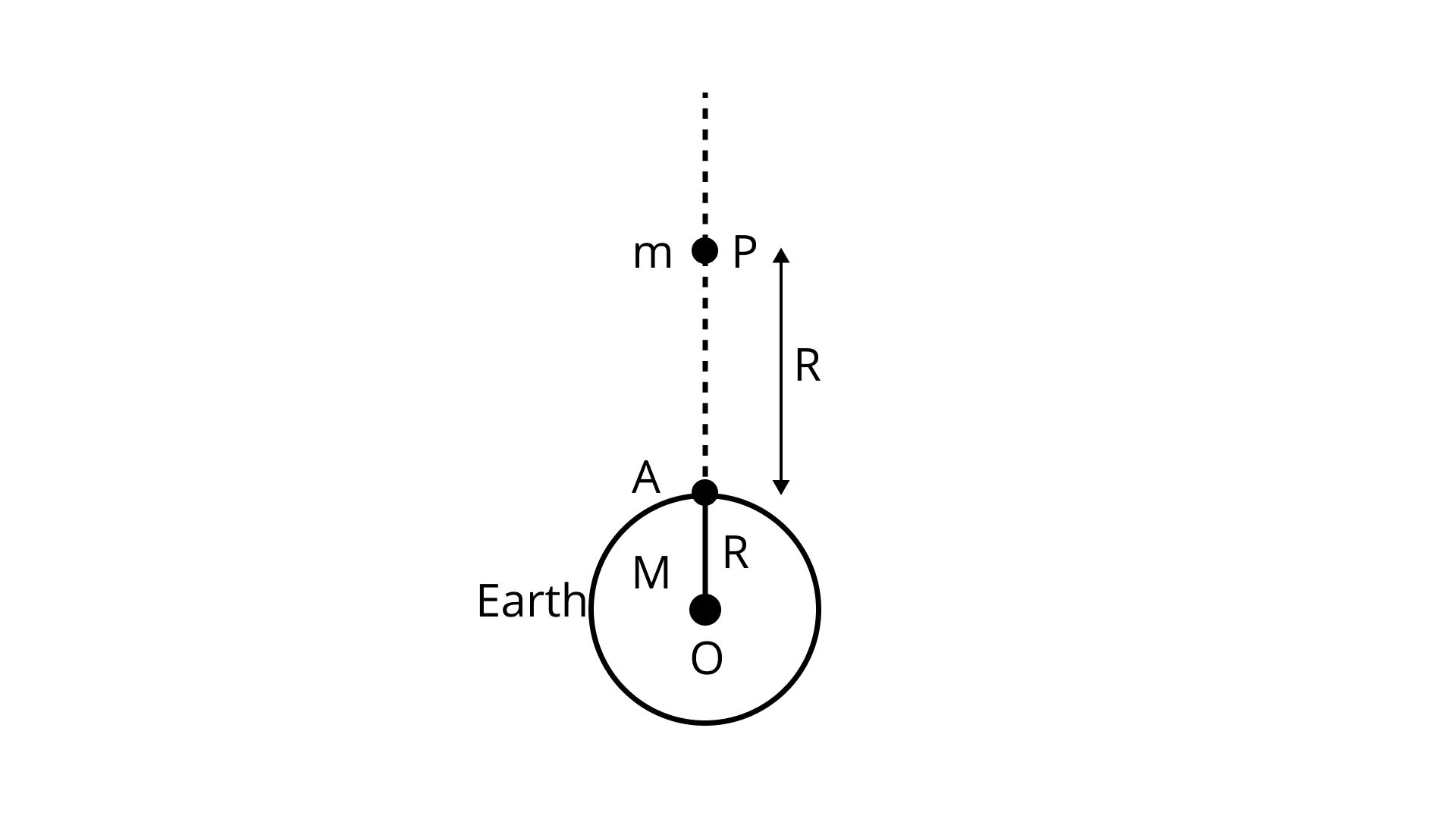
Here P.E, is equal to radius of earth i.e. ${\text{ =  }}\dfrac{{{\text{ - GMm}}}}{{{\text{(2R)}}}}$

Gain ${\text{ =  }}{{\text{E}}_{{{\text{p}}^{\text{'}}}}}{\text{ - }}{{\text{E}}_{{\text{pi}}}}$

which  is equal to ${\text{ =  }}\dfrac{{{\text{ - GMm}}}}{{{\text{2R}}}}{\text{ - }}\left( {\dfrac{{{\text{ - GMm}}}}{{\text{R}}}} \right)$

  ${\text{ =  }}\dfrac{{{\text{GMm}}}}{{\text{R}}}\left[ {{\text{ - }}\dfrac{{\text{1}}}{{\text{2}}}{\text{ + 1}}} \right]$

  ${\text{ =  }}\dfrac{{{\text{GMm}}}}{{{\text{2R}}}}$

GM ${\text{ =  g}}{{\text{R}}^{\text{2}}}$

Thus, gain in potential energy ${\text{ =  }}\dfrac{{{\text{g}}{{\text{R}}^{\text{2}}}{\text{m}}}}{{{\text{2R}}}}{\text{  =  }}\dfrac{{\text{1}}}{{\text{2}}}{\text{mgR}}$

33. A mass ${\text{m}}$ is placed at P a distance ${\text{h}}$ along the normal through the centre ${\text{O}}$ of a thin circular ring of mass ${\text{M}}$ and radius ${\text{r}}$ (Figure).

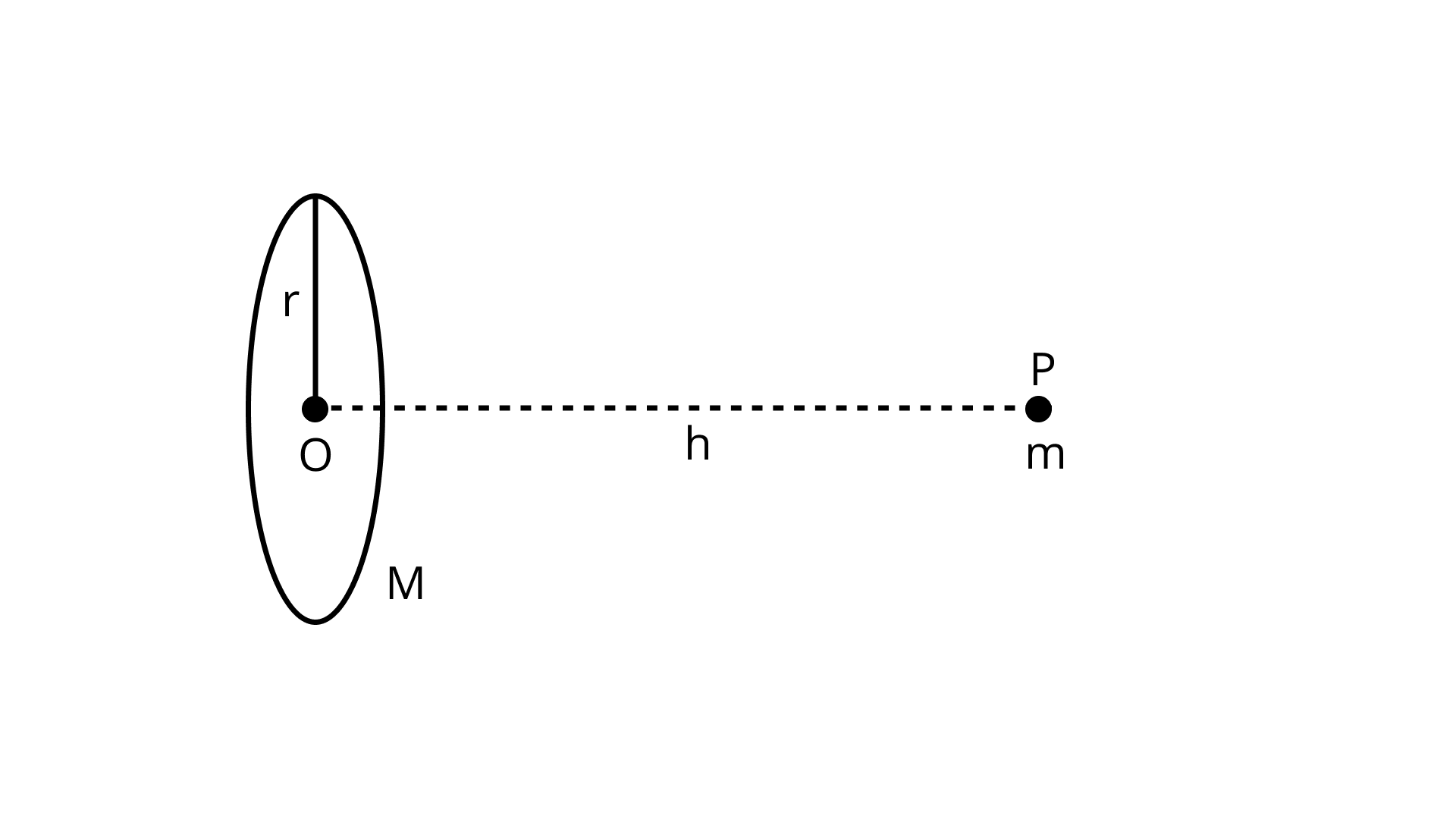
If the mass ${\text{m}}$ is removed further away such that OP becomes ${\text{2h}}$ , by what factor the force of gravitation will decrease, if ${\text{h  =  r}}$

Ans: Here let a ring with radius ${\text{r}}$ and mass ${\text{M}}$ and let if mass ${\text{m}}$ is placed at distant ${\text{h}}$ at point P. Now, consider element (small) of ring with mass ${\text{dM}}$ at point A

Assume distance between ${\text{dM}}$ and ${\text{m}}$ be ${\text{x}}$

And ${{\text{x}}^{\text{2}}}{\text{  =  }}{{\text{r}}^{\text{2}}}{\text{ + }}{{\text{h}}^{\text{2}}}$

Also assume that gravitational force between ${\text{dM}}$ and ${\text{m}}$, ${\text{dF  =  }}\dfrac{{{\text{G(dM)m}}}}{{{{\text{x}}^{\text{2}}}}}$

So, ${\text{dF}}$ has two components i.e. ${\text{dF Cos}\theta{ }}$ along PO and ${\text{dF sin}\theta{ }}$ perpendicular to PO

Thus, $\int {\text{d}} {\text{F sin}\theta{   =  0}}$

Net force on ${\text{m}}$ is ${\text{F  =  }}\int {\text{d}} {\text{F cos}\theta{   =  }}\int {\dfrac{{{\text{G(dM)m}}}}{{{{\text{x}}^{\text{2}}}}}} {\text{ }\times{ }}\dfrac{{\text{h}}}{{\text{x}}}$

                               ${\text{ =  }}\dfrac{{{\text{Gmh}}}}{{{{\text{x}}^{\text{3}}}}}\int {\text{d}} {\text{M  =  }}\dfrac{{{\text{GMmh}}}}{{{{\text{x}}^{\text{3}}}}}{\text{  =  }}\dfrac{{{\text{GMmh}}}}{{{{\left( {{{\text{r}}^{\text{2}}}{\text{ + }}{{\text{h}}^{\text{2}}}} \right)}^{{\text{3/2}}}}}}$                                    (i)

Now, when mass is displaced at distance 

$\mathrm{F}^{\prime}=\dfrac{\mathrm{GMm} 2 \mathrm{~h}}{\left(\mathrm{r}^{2}+(2 \mathrm{~h})^{2}\right)^{3 / 2}}=\dfrac{\mathrm{GMm} 2 \mathrm{~h}}{\left(\mathrm{r}^{2}+4 \mathrm{~h}^{2}\right)^{3 / 2}}$

When $\mathrm{h}=\mathrm{r}$

So, From equation (i) we get: 

$\quad \mathrm{F}=\dfrac{\mathrm{GMmr}}{\left(\mathrm{r}^{2}+\mathrm{r}^{2}\right)^{3 / 2}}=\dfrac{\mathrm{GMm}}{2 \sqrt{2} \mathrm{r}^{2}}$

$\mathrm{F}^{\prime}=\dfrac{\mathrm{GMmr}}{\left(\mathrm{r}^{2}+4 \mathrm{r}^{2}\right)^{3 / 2}}=\dfrac{2 \mathrm{GMm}}{5 \sqrt{5} \mathrm{r}^{2}}$

Now, equation (iv) and equation (iii), we get:

$\dfrac{\mathrm{F}^{\prime}}{\mathrm{F}}=\dfrac{4 \sqrt{2}}{5 \sqrt{5}}$

$\mathrm{~F}^{\prime}=\dfrac{4 \sqrt{2}}{5 \sqrt{5}} \mathrm{~F}$

which is the gravitational force between mass and ring at a distant of $2 \mathrm{~h}$

Long Answer Type Questions

34. A star like the sun has several bodies moving around it at different distances. Consider that all of them are moving in circular orbits. Let ${\text{r}}$ be the distance of the body from the centre of the star and let its linear velocity be ${\text{v}}$ , angular velocity ${\text{}\omega{ }}$ , kinetic energy ${\text{k}}$ , gravitational potential energy ${\text{U}}$ , total energy ${\text{E}}$ and angular momentum ${\text{l}}$ . As the radius ${\text{r}}$ of the orbit increases, determine which of the above quantities increase and which ones decrease.

Ans: according to equilibrium condition, when body moves around star, so gravitational pull results in centripetal force.

Now, consider mass ${\text{m}}$ is rotating around star ${\text{S}}$ of mass ${\text{M}}$ whose radius is ${\text{r}}$

${{\text{F}}_{\text{c}}}{\text{  =  }}\dfrac{{{\text{mv}}_{\text{0}}^{\text{2}}}}{{\text{r}}}{\text{  =  }}\dfrac{{{\text{GMm}}}}{{{{\text{r}}^{\text{2}}}}}$   

(i) Orbital velocity ${{\text{v}}_{\text{0}}}{\text{  =  }}\sqrt {\dfrac{{{\text{GM}}}}{{\text{r}}}} {\text{ }} \Rightarrow {\text{ }}{{\text{v}}_{\text{0}}} \propto \dfrac{{\text{1}}}{{\sqrt {\text{r}} }}$

So, orbital velocity decreases on increasing radius of circular path

(ii) Angular velocity ${\text{}\omega{   =  }}\dfrac{{{\text{2}\pi{ }}}}{{\text{T}}}{\text{, }}{{\text{T}}^{\text{2}}} \propto {{\text{r}}^{\text{3}}}$ which is followed by Kepler’s third law

${\text{}\omega{   =  }}\dfrac{{{\text{2}\pi{ }}}}{{{\text{K}}{{\text{r}}^{\dfrac{3}{2}}}}}{\text{, }\omega{ }} \propto \dfrac{1}{{\sqrt {{{\text{r}}^3}} }}$

Thus, angular velocity decreases on increasing radius of circular orbit

(iii) Kinetic energy ${{\text{E}}_{\text{k}}}{\text{  =  }}\dfrac{{\text{1}}}{{\text{2}}}{\text{m}}\dfrac{{{\text{GM}}}}{{\text{r}}}{\text{ }} \Rightarrow {\text{ }}{{\text{E}}_{\text{k}}} \propto \dfrac{{\text{1}}}{{\text{r}}}$

Thus, kinetic energy decreases on increasing radius of circular path

(iv) Gravitational potential energy 

${{\text{E}}_{\text{p}}}{\text{  =  }}\dfrac{{{\text{ - GMm}}}}{{\text{r}}}{\text{ }} \Rightarrow {\text{ }}{{\text{E}}_{\text{p}}} \propto {\text{ - }}\left( {\dfrac{{\text{1}}}{{\text{r}}}} \right)$

Hence, potential energy increases on increasing radius of circular orbit

(v) Total energy $\mathrm{E}=\mathrm{E}_{\mathrm{k}}+\mathrm{E}_{\mathrm{p}}=\frac{\mathrm{GMm}}{2 \mathrm{r}}+\left(\frac{-\mathrm{GMm}}{\mathrm{r}}\right)=\frac{-\mathrm{GMm}}{2 \mathrm{r}}$

Thus, total energy increases on increasing radius of circular orbit

(vi) Angular momentum 

${\text{L  =  mv}\gamma{   =  m}}\sqrt {\dfrac{{{\text{GM}}}}{{\text{r}}}} {\text{r  =  m}}\sqrt {{\text{GMr}}} {\text{ }} \Rightarrow {\text{ L}} \propto \sqrt {\text{r}}$

Thus, angular momentum increases on increasing radius of circular orbit

35. Six points masses of mass ${\text{m}}$ each are at the vertices of a regular hexagon of side ${\text{l}}$  Calculate the force on any of the masses.

Ans: AE ${\text{ = }}$ AG ${\text{ + }}$ EG ${\text{ = }}$ AG ${\text{ + }}$ AG ${\text{ = }}$ ${\text{2}}$ $AG$ ${\text{ = }}$ ${\text{2 l cos3}}{{\text{0}}^\circ}$

  ${\text{AE  =  2l}}\dfrac{{\sqrt {\text{3}} }}{{\text{2}}}{\text{  =  }}\sqrt {\text{3}} {\text{l}}$

  ${\text{AE  =  AC  =  }}\sqrt {\text{3}} {\text{ l}}$

  ${\text{AD  =  DH + HI + AI}}$

 ${\text{ =  AI + l + AI  =  l + 2AI}}$

  ${\text{ =  l + 2AB cos6}}{{\text{0}}^\circ}$

  ${\text{ =  l + 2l }\times{ }}\dfrac{{\text{1}}}{{\text{2}}}{\text{  =  2 l}}$ 

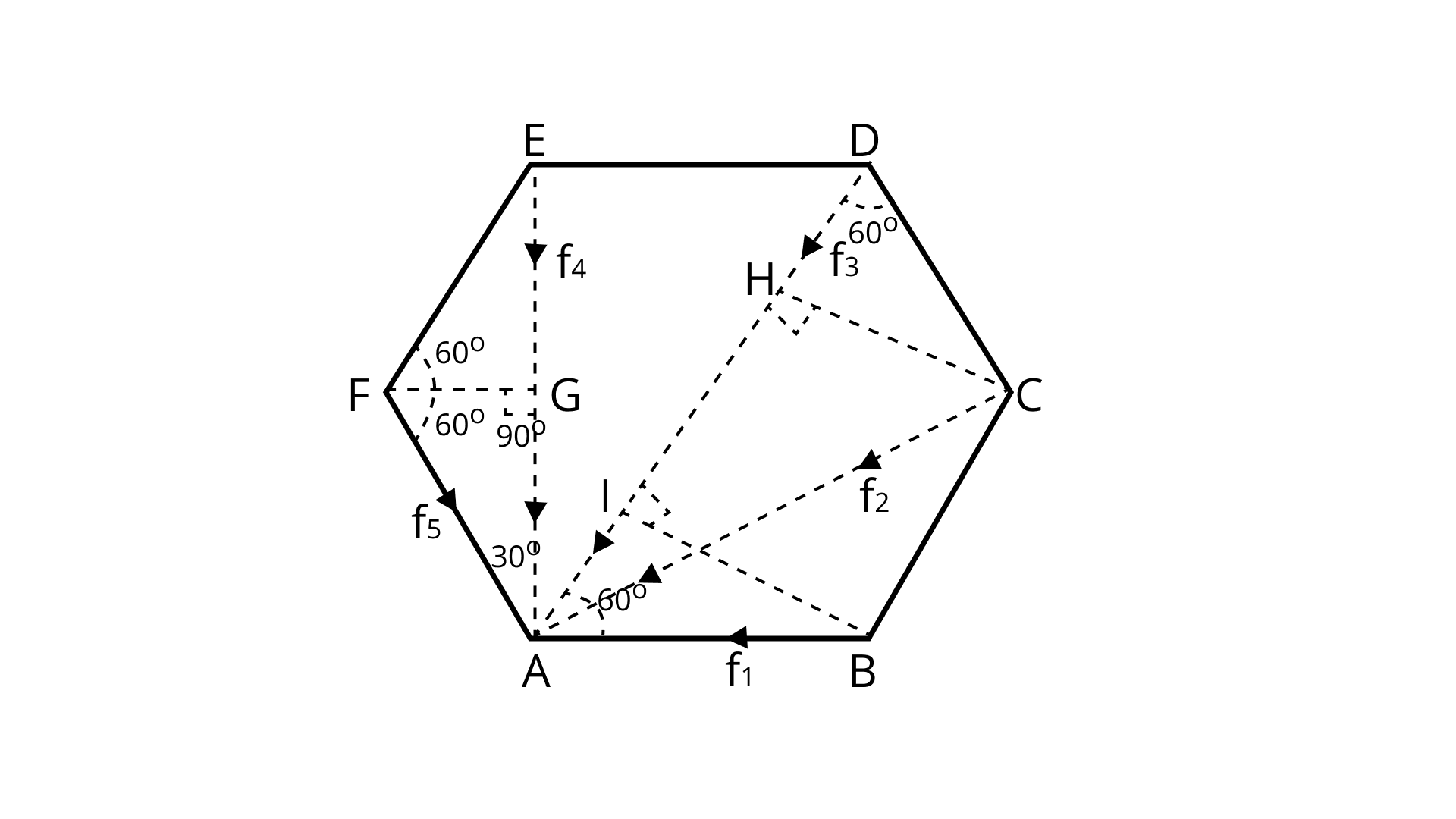
${\text{AD  =  2l}}$

Force on A due to B ${\text{ =  }}{{\text{f}}_{\text{1}}}{\text{  =  }}\dfrac{{{\text{Gmm}}}}{{{{\text{l}}^{\text{2}}}}}{\text{  =  }}\dfrac{{{\text{G}}{{\text{m}}^{\text{2}}}}}{{{{\text{l}}^{\text{2}}}}}$ along B to A 

Force on A due to C ${\text{ =  }}{{\text{f}}_{\text{2}}}{\text{  =  }}\dfrac{{{\text{Gmm}}}}{{{{{\text{(}}\sqrt {\text{3}} {\text{l)}}}^{\text{2}}}}}{\text{  =  }}\dfrac{{{\text{G}}{{\text{m}}^{\text{2}}}}}{{{\text{3}}{{\text{l}}^{\text{2}}}}}$ along C to A

Force on A due to D ${\text{ =  }}{{\text{f}}_{\text{3}}}{\text{  =  }}\dfrac{{{\text{Gmm}}}}{{{{{\text{(2l)}}}^{\text{2}}}}}{\text{  =  }}\dfrac{{{\text{G}}{{\text{m}}^{\text{2}}}}}{{{\text{4}}{{\text{l}}^{\text{2}}}}}$ along D to A

Force on A due to E ${\text{ =  }}{{\text{f}}_{\text{4}}}{\text{  =  }}\dfrac{{{\text{Gmm}}}}{{{{{\text{(}}\sqrt {\text{3}} {\text{l)}}}^{\text{2}}}}}{\text{  =  }}\dfrac{{{\text{G}}{{\text{m}}^{\text{2}}}}}{{{\text{3}}{{\text{l}}^{\text{2}}}}}$ along E to A

Force on A due to F ${\text{ =  }}{{\text{f}}_5}{\text{  =  }}\dfrac{{{\text{Gmm}}}}{{{{{\text{(l)}}}^{\text{2}}}}}{\text{  =  }}\dfrac{{{\text{G}}{{\text{m}}^{\text{2}}}}}{{{{\text{l}}^{\text{2}}}}}$

$\overrightarrow{F_{1}^{2}}=\overrightarrow{F_{1}}+\overrightarrow{F_{5}}=\left(f_{1}\right)^{2}+\left(f_{5}\right)^{2}+2 f_{1} f_{5} \cos 120^{\circ}$

$=\left(\dfrac{G m^{2}}{I^{2}}\right)^{2}+\left(\dfrac{G m^{2}}{I^{2}}\right)^{2}+2\left(\dfrac{G m^{2}}{I^{2}}\right)^{2} \cos \left(90^{\circ}+30^{\circ}\right)$

$=\left[\dfrac{G m^{2}}{I^{2}}\right]^{2}\left[1+1-2 \sin 30^{\circ}\right]$

$\mathrm{F}_{1}=\sqrt{\left(\sqrt{\dfrac{\mathrm{Gm}^{2}}{\mathrm{I}^{2}}}\right)^{2}\left[1+\mathrm{l}-2 \times \dfrac{1}{2}\right]}=\sqrt{\dfrac{\mathrm{Gm}^{2}}{\mathrm{I}^{2}}}=\dfrac{\mathrm{Gm}^{2}}{\mathrm{I}^{2}}$

$\overrightarrow{\mathrm{F}_{2}^{2}}=\left[\overrightarrow{\mathrm{F}_{2}}+\overrightarrow{\mathrm{F}_{4}}\right]=\mathrm{f}_{2}^{2}+\mathrm{f}_{4}^{2}+2 \mathrm{f}_{2} \mathrm{f}_{4} \cos 60^{\circ}$

$\mathrm{F}_{2}^{2}=\left(\dfrac{\mathrm{Gm}^{2}}{3 \mathrm{l}^{2}}\right)^{2}[1+1+1]$

$\mathrm{F}_{2}=\dfrac{\mathrm{Gm}^{2}}{3 \mathrm{l}^{2}} \sqrt{3} \dfrac{\mathrm{Gm}^{2}}{\sqrt{3} \mathrm{l}^{2}}$

$\mathrm{~F}_{3}=\dfrac{\mathrm{Gm}^{2}}{4 \mathrm{l}^{2}}$

$\mathrm{~F}=\mathrm{F}_{1}+\mathrm{F}_{2}+\mathrm{F}_{3}=\dfrac{\mathrm{Gm}^{2}}{\mathrm{l}^{2}}+\dfrac{\mathrm{Gm}^{2}}{\sqrt{3} \mathrm{l}^{2}}+\dfrac{\mathrm{Gm}^{2}}{4 \mathrm{l}^{2}}$

$\mathrm{~F}=\dfrac{\mathrm{Gm}^{2}}{\mathrm{l}^{2}}\left[1+\dfrac{1}{\sqrt{3}}+\dfrac{1}{4}\right]$ along DA

36. A satellite is to be placed in equatorial geostationary orbit around earth for communication.

  ${{\text{M  =  6 }\times{ 1}}{{{0}}^{{{24}}}}{\text{kg, R  =  6400 Km, T  =  24h,}}}$ 

  ${{\text{G  =  6}}{\text{.67 }\times{ 1}}{{\text{0}}^{{\text{ - 11}}}}{\text{ SI units }}}$ 

(a) Calculate height of such a satellite.

Ans: We have given that mass $\mathrm{M}=6 \times 10^{24} \mathrm{~kg}$

Radius $R=6400 \mathrm{~km}=6.4 \times 10^{6} \mathrm{~m}$

Time period $=24 \mathrm{~h}=24 \times 3600 \mathrm{~s}=24 \times 36 \times 10^{2} \mathrm{~s}$

$\mathrm{G}=6.67 \times 10^{-11} \mathrm{~N}-\mathrm{m}^{2} \mathrm{~kg}^{-2}$

Orbital radius $=\mathrm{R}+\mathrm{h}$

Here ${\text{h}}$ be the height of satellite

So, orbital velocity is

  ${{\text{v}}_{\text{0}}}{\text{  =  }}\sqrt {\dfrac{{{\text{GM}}}}{{{\text{R + h}}}}}$

  ${\text{v}}_{\text{0}}^{\text{2}}{\text{  =  }}\dfrac{{{\text{GM}}}}{{{\text{(R + h)}}}}$

  ${{\text{v}}_{\text{0}}}{\text{  =  }}\sqrt {\dfrac{{{\text{GM}}}}{{{\text{r + h}}}}}$

  ${\text{T  =  }}\dfrac{{{\text{2}\pi{ (R + h)}}}}{{{{\text{v}}_{\text{0}}}}}$

  ${{\text{T}}^{\text{2}}}{\text{  =  }}\dfrac{{{\text{4}}{{\text{}\pi{ }}^{\text{2}}}{{{\text{(R + h)}}}^{\text{2}}}{\text{(R + h)}}}}{{{\text{GM}}}}{\text{  =  }}\dfrac{{{\text{4}}{{\text{}\pi{ }}^{\text{2}}}{{{\text{(R + h)}}}^{\text{3}}}}}{{{\text{GM}}}}{\text{ , (R + h)  =  }}{\left[ {\dfrac{{{\text{G}}{{\text{T}}^{\text{2}}}{\text{M}}}}{{{\text{4}}{{\text{}\pi{ }}^{\text{2}}}}}} \right]^{\dfrac{1}{3}}}$

 ${\text{h  =  }}{\left[ {\dfrac{{{\text{G}}{{\text{T}}^{\text{2}}}{\text{M}}}}{{{\text{4}}{{\text{}\pi{ }}^{\text{2}}}}}} \right]^{\dfrac{1}{3}}}{\text{ - R}}$ 

${\text{h  =  }}{\left[ {\dfrac{{{\text{6}}{\text{.67 }\times{ 1}}{{\text{0}}^{{\text{ - 11}}}}{\text{ }\times{ (24 }\times{ 36}}{{\text{)}}^{\text{2}}}{\text{ }\times{ }}{{\left( {{\text{1}}{{\text{0}}^{\text{2}}}} \right)}^{\text{2}}}{\text{ }\times{ 6 }\times{ 1}}{{\text{0}}^{{\text{24}}}}}}{{{\text{4 }\times{ 3}}{\text{.14 }\times{ 3}}{\text{.14}}}}} \right]^{{\text{1/3}}}}{\text{ - 6}}{\text{.4 }\times{ 1}}{{\text{0}}^{\text{6}}}$

${\text{h  =  }}\left[ {\dfrac{{{\text{167 }\times{ 2}}{{\text{4}}^{\text{2}}}{\text{ }\times{ 3}}{{\text{6}}^{\text{2}}}{\text{ }\times{ 6 }\times{ 1}}{{\text{0}}^{{\text{ - 11 + 4 + 24 + 2}}}}}}{{{\text{314 }\times{ 314}}}}} \right]{\text{ - 6}}{\text{.4 }\times{ 1}}{{\text{0}}^{\text{6}}}$

  ${\text{h  =  }}{\left[ {\dfrac{{{\text{167 }\times{ 2}}{{\text{4}}^{\text{2}}}{\text{ }\times{ 3}}{{\text{6}}^{\text{2}}}{\text{ }\times{ 6 }\times{ 1}}{{\text{0}}^{{\text{ - 40}}}}}}{{{\text{314 }\times{ 314}}}}} \right]^{{\text{13}}}}{\text{ - 6}}{\text{.4 }\times{ 1}}{{\text{0}}^{\text{6}}}$

  ${\text{h  =  x - 6}}{\text{.4 }\times{ 1}}{{\text{0}}^{\text{6}}}$

  ${\text{log x  =  }}\dfrac{{\text{1}}}{{\text{3}}}\left[ {{\text{log}}{{\text{N}}^{\text{r}}}{\text{ - log}}{{\text{D}}^{\text{r}}}} \right]$

So, consider values of 

${\text{log }}{{\text{N}}^{\text{r}}}{\text{  =  2}}{\text{.2227 + 1}}{\text{.3802 + 1}}{\text{.3802 + 1}}{\text{.5563 + 1}}{\text{.5563 + 0}}{\text{.7782 + 19}}{\text{.0000}}$

                                               ${\text{ =  27}}{\text{.8739}}$

And value of 

${\text{ - log }}{{\text{D}}^{\text{r}}}{\text{  =  2}}{\text{.4969 + 2}}{\text{.4969  =  4}}{\text{.9938}}$

Thus, ${\text{log }}{{\text{N}}^{\text{r}}}{\text{  -  log}}{{\text{D}}^{\text{r}}}{\text{  =  27}}{\text{.8739 - 4}}{\text{.9938  =  22}}{\text{.8801}}$

${\text{log x  =  }}\dfrac{1}{3}\times 22.8801{\text{  =  7}}{\text{.6267}}$

  ${\text{x  =  4}}{\text{.2335 }\times{ 1}}{{\text{0}}^{\text{7}}}$

  ${\text{h  =  42}}{\text{.335 }\times{ 1}}{{\text{0}}^{\text{6}}}{\text{ - 6}}{\text{.4 }\times{ 1}}{{\text{0}}^{\text{6}}}$

  ${\text{ =  (42}}{\text{.335 - 6}}{\text{.4) }\times{ 1}}{{\text{0}}^{\text{6}}}{\text{m}}$

  ${\text{ =  35}}{\text{.94 }\times{ 1}}{{\text{0}}^{\text{3}}}{\text{ }\times{ 1}}{{\text{0}}^{\text{3}}}{\text{m  =  35}}{\text{.94 }\times{ 1}}{{\text{0}}^{\text{3}}}{\text{km}}$

  ${\text{h  =  35940km}}$

(b) Find out the minimum number of satellites that are needed to cover entire earth so that at least one satellites is visible from any point on the equator. 

Ans: Let satellite S at ${\text{h m}}$ which is above the earth surface.

Let angle subtended by satellite be ${\text{2}\theta {}}$ . Then in right angled triangle SPO

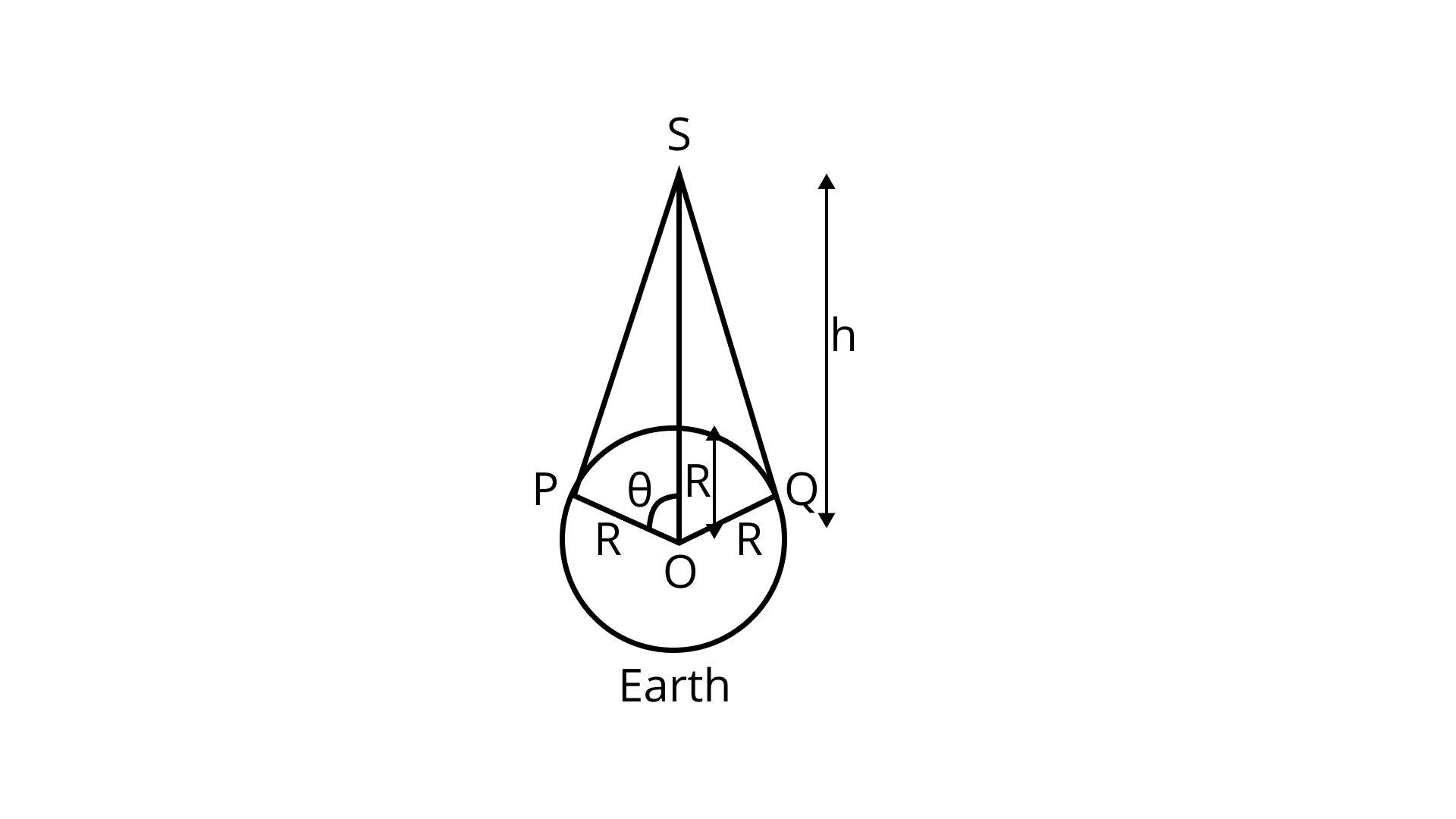
${\text{cos}\theta{   =  }}\dfrac{{\text{R}}}{{{\text{R + h}}}}{\text{  =  }}\dfrac{{\text{R}}}{{{\text{R}}\left[ {{\text{1 + }}\dfrac{{\text{h}}}{{\text{R}}}} \right]}}$

  ${\text{cos}\theta{   =  }}\dfrac{{\text{1}}}{{\left[ {{\text{1 + }}\dfrac{{\text{h}}}{{\text{R}}}} \right]}}$

  ${\text{h  =  3}}{\text{.59 }\times{ 1}}{{\text{0}}^{\text{7}}}{\text{m}}$

${\text{R  =  6}}{\text{.4 }\times{ 1}}{{\text{0}}^{\text{6}}}{\text{m}}$

  ${\text{cos}\theta{   =  }}\dfrac{{\text{1}}}{{\left[ {{\text{1 + }}\dfrac{{\text{h}}}{{\text{R}}}} \right]}}{\text{  =  }}\dfrac{{\text{1}}}{{\left[ {{\text{1 + }}\dfrac{{{\text{3}}{\text{.59 }\times{ 1}}{{\text{0}}^{\text{7}}}}}{{{\text{6}}{\text{.40 }\times{ 1}}{{\text{0}}^{\text{6}}}}}} \right]}}$

  ${\text{ =  }}\dfrac{{\text{1}}}{{{\text{1 + }}\dfrac{{{\text{3590}}}}{{{\text{640}}}}{\text{ }\times{ }}\dfrac{{{\text{1}}{{\text{0}}^{\text{6}}}}}{{{\text{1}}{{\text{0}}^{\text{6}}}}}}}{\text{  =  }}\dfrac{{\text{1}}}{{{\text{1 + 5}}{\text{.6}}}}{\text{  =  }}\dfrac{{\text{1}}}{{{\text{6}}{\text{.6}}}}$ 

${\text{cos}}\theta{{   =  0}}{\text{.1515}}$

${\text{}\theta{   =  81}}{\text{.2}}{{\text{8}}^\circ }$ 

${\text{2}\theta{   =  [81}}{\text{.28 }\times{ 2]}}$ covered by one satellite

So, Total angle ${\text{ =  36}}{{\text{0}}^\circ}$

No. of satellite which cover ${\text{36}}{{\text{0}}^\circ}$ 

${\text{ =  }}\dfrac{{{\text{36}}{{\text{0}}^\circ}}}{{{\text{81}}{\text{.28 }\times{ 2}}}}{\text{  =  2}}{\text{.21}}$

37. Earth's orbit is an ellipse with eccentricity ${\text{0}}{\text{.0167}}$ . Thus, earth's distance from the sun and speed as it moves around the sun varies from day to day. This means that the length of the solar day is not constant throughout the year. Assume that earth's spin axis is normal to its orbital plane and find out the length of the shortest and the longest day. A day should be taken from noon to noon. Does this explain variation of length of the day during the year?

Ans: Here eccentricity denoted as ${\text{e}}$ and semi major axis denoted as ${\text{a}}$

So, aphelion and perihelion distances are

${{\text{r}}_{\text{p}}}{\text{  =  a(1 - e), }}{{\text{r}}_{\text{a}}}{\text{  =  a(1 + e)}}$

Since earth orbits the sun, so angular momentum is conserved.

Let mass be ${\text{m}}$ , Linear velocity be ${{\text{v}}_{\text{p}}}$ , Angular velocity be ${{\text{}\omega{ }}_{\text{a}}}$ of earth around sun at perigee position P. 

And ${{\text{v}}_{\text{a}}}{\text{, }}{{\text{}\omega{ }}_{\text{a}}}$ denotes linear and angular velocity respectively, of earth at apogee position A

Now, from Kepler’s second law, we have $\dfrac{{{\text{dA}}}}{{{\text{dt}}}}{\text{  =  }}\dfrac{{\text{L}}}{{{\text{2m}}}}{\text{  =  constant}}$

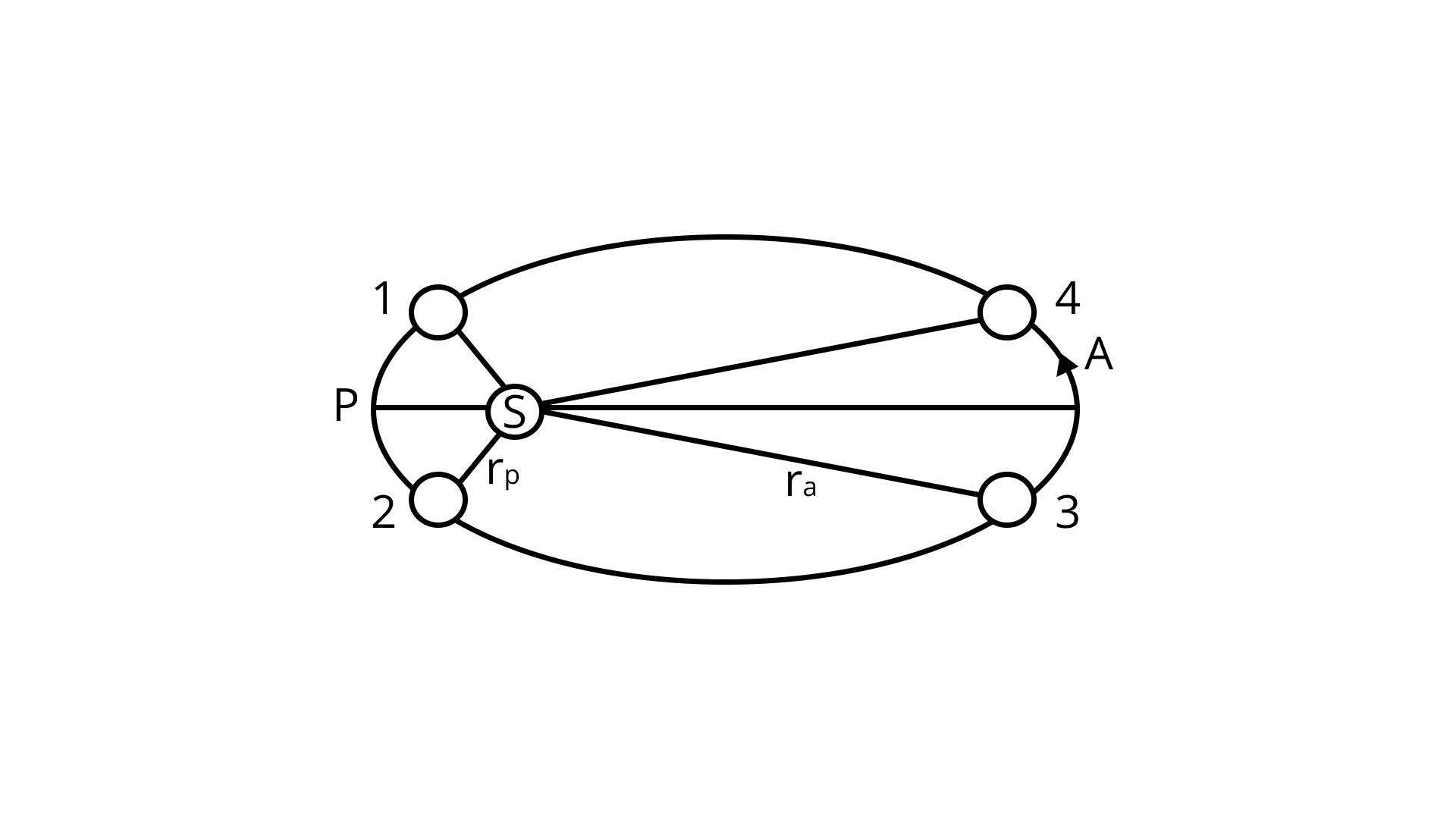
${{\text{L}}_{\text{a}}}{\text{  =  }}{{\text{L}}_{\text{p}}}$

${{\text{r}}_{\text{a}}}{\text{ }\times{ }}{{\text{p}}_{\text{a}}}{\text{  =  }}{{\text{r}}_{\text{p}}}{\text{ }\times{ }}{{\text{p}}_{\text{p}}}$

${{\text{r}}_{\text{a}}}{\text{ }\times{ m}}{{\text{v}}_{\text{a}}}{\text{  =  }}{{\text{r}}_{\text{p}}}{\text{ }\times{ m}}{{\text{v}}_{\text{p}}}$

${{\text{r}}_{\text{a}}}{\text{ }\times{ m}}{{\text{}\omega{ }}_{\text{a}}}{{\text{r}}_{\text{a}}}{\text{  =  }}{{\text{r}}_{\text{p}}}{\text{ }\times{ m}}{{\text{}\omega{ }}_{\text{p}}}{{\text{r}}_{\text{p}}}$

 ${{\text{}\omega{ }}_{\text{a}}}{\text{r}}_{\text{a}}^{\text{2}}{\text{  =  }}{{\text{}\omega{ }}_{\text{p}}}{\text{r}}_{\text{p}}^{\text{2}}$

  $\dfrac{{{{\text{}\omega{ }}_{\text{p}}}}}{{{{\text{}\omega{ }}_{\text{a}}}}}{\text{  =  }}\dfrac{{{\text{r}}_{\text{a}}^{\text{2}}}}{{{\text{r}}_{\text{p}}^{\text{2}}}}{\text{  =  }}{\left( {\dfrac{{{{\text{r}}_{\text{a}}}}}{{{{\text{r}}_{\text{p}}}}}} \right)^{\text{2}}}$

  $\because {\text{ }}{{\text{r}}_{\text{p}}}{\text{  =  a(1 - e)}}$ 

${{\text{r}}_{\text{a}}}{\text{  =  a(1 + e)}}$

  $\dfrac{{{{\text{}\omega{ }}_{\text{p}}}}}{{{{\text{}\omega{ }}_{\text{a}}}}}{\text{  =  }}{\left[ {\dfrac{{{\text{a(1 + e)}}}}{{{\text{a(1 - e)}}}}} \right]^{\text{2}}}{\text{, e  =  0}}{\text{.0167}}$

$\dfrac{{{{\text{}\omega{ }}_{\text{p}}}}}{{{{\text{}\omega{ }}_{\text{a}}}}}{\text{  =  }}\dfrac{{{{{\text{(1 + 0}}{\text{.0167)}}}^{\text{2}}}}}{{{{{\text{(1 - 0}}{\text{.0167)}}}^{\text{2}}}}}{\text{  =  }}{\left( {\dfrac{{{\text{1}}{\text{.0167}}}}{{{\text{.9833}}}}} \right)^{\text{2}}}{\text{  =  (1}}{\text{.0339}}{{\text{)}}^{\text{2}}}{\text{  =  1}}{\text{.0691}}$ 

If ${\text{}\omega{ }}$ be mean angular speed of earth then we have

  $\dfrac{{{{\text{}\omega{ }}_{\text{p}}}}}{{\text{}\omega{ }}}{\text{ }\times{ }}\dfrac{{\text{}\omega{ }}}{{{{\text{}\omega{ }}_{\text{a}}}}}{\text{  =  1}}{\text{.0691}}$

  $\dfrac{{{{\text{}\omega{ }}_{\text{p}}}}}{{\text{}\omega{ }}}{\text{  =  }}\dfrac{{\text{}\omega{ }}}{{{{\text{}\omega{ }}_{\text{a}}}}}{\text{  =  }}\sqrt {{\text{1}}{\text{.0691}}} {\text{  =  1}}{\text{.034}}$

If ${\text{}\omega{ }}$ is one degree which is corresponds to one day i.e. average angular speed ${{\text{}\omega{ }}_{\text{0}}}{\text{  =  1}}{\text{.03}}{{\text{4}}^\circ}$ per day and ${{\text{}\omega{ }}_{\text{a}}}{\text{  =  0}}{\text{.983}}{{\text{3}}^\circ}{\text{, }}{{\text{}\omega{ }}_{\text{p}}}{\text{  =  1}}{\text{.016}}{{\text{7}}^\circ}$ per day. As ${\text{36}}{{\text{1}}^{\text{0}}}{\text{  =  24 hrs}}$ .

So, we get $361.034^{\circ}$ corresponds to 24 hrs $8.14^{\prime}$ ( $8.1^{\prime}$ longer), $360.967^{\circ}$ corresponds to 23 hrs 59 min, $52^{\prime}$ ( $7.9$ 'smaller)

38. A satellite is in an elliptic orbit around the earth with aphelion of ${\text{6R}}$ and perihelion of ${\text{2R}}$ where ${\text{R  =  6400 km}}$ is the radius of the earth. Find eccentricity of the orbit. Find the velocity of the satellite at apogee and perigee. What should be done if this satellite has to be transferred to a circular orbit of radius ${\text{6R}}$ $\left[ {{\text{G  =  6}}{\text{.67 }\times{ 1}}{{\text{0}}^{{\text{ - 11}}}}{\text{ SI}}} \right.{\text{ units and }}\left. {{\text{M  =  6 }\times{ 1}}{{\text{0}}^{{\text{24}}}}{\text{kg}}} \right]$

Ans: ${{\text{r}}_{\text{p}}}{\text{  =  2R, }}{{\text{r}}_{\text{a}}}{\text{  =  6R}}$

Thus, ${{\text{r}}_{\text{p}}}{\text{  =  a(1 - e)  =  2R}}$                            (i)

${{\text{r}}_{\text{a}}}{\text{  =  a(1 + e)  =  6R}}$                                    (ii)

Now, divide (i) by (ii), we get

  $\dfrac{{{\text{1 - e}}}}{{{\text{1 + e}}}}{\text{  =  }}\dfrac{{\text{2}}}{{\text{6}}}$

  ${\text{3 - 3e  =  1 + e}}$

  ${\text{4e  =  2}}$

  ${\text{e  =  }}\dfrac{{\text{1}}}{{\text{2}}}$ 

So, There is not external force. Thus by law of consvervation of angular momentum:

${{\text{L}}_{\text{1}}}{\text{  =  }}{{\text{L}}_{\text{2}}}$

${{\text{m}}_{\text{a}}}{{\text{v}}_{\text{a}}}{{\text{r}}_{\text{a}}}{\text{  =  }}{{\text{m}}_{\text{p}}}{{\text{v}}_{\text{p}}}{{\text{r}}_{\text{p}}}$ 

${{\text{m}}_{\text{a}}}{\text{  =  }}{{\text{m}}_{\text{p}}}{\text{  =  m  = }}$ mass of satellite

$\dfrac{{{{\text{v}}_{\text{a}}}}}{{{{\text{v}}_{\text{p}}}}}{\text{  =  }}\dfrac{{{{\text{r}}_{\text{p}}}}}{{{{\text{r}}_{\text{a}}}}}\dfrac{{{\text{2R}}}}{{{\text{6R}}}}{\text{  =  }}\dfrac{{\text{1}}}{{\text{3}}}$

${{\text{}\nu{ }}_{\text{p}}}{\text{  =  3}}{{\text{}\nu{ }}_{\text{a}}}$ 

Now, apply conservation of energy at apogee and perigee, we get:

$\dfrac{{\text{1}}}{{\text{2}}}{\text{mv}}_{\text{p}}^{\text{2}}{\text{ - }}\dfrac{{{\text{GMm}}}}{{{{\text{r}}_{\text{p}}}}}{\text{  =  }}\dfrac{{\text{1}}}{{\text{2}}}{\text{mv}}_{\text{a}}^{\text{2}}{\text{ - }}\dfrac{{{\text{GMm}}}}{{{{\text{r}}_{\text{a}}}}}$

Multiply by $\dfrac{{\text{2}}}{{\text{m}}}$ on both sides and put ${{\text{r}}_{\text{p}}}{\text{  =  2R, }}{{\text{r}}_{\text{a}}}{\text{  =  6R}}$ we get:

${\text{v}}_{\text{p}}^{\text{2}}{\text{ - }}\dfrac{{{\text{2GM}}}}{{{\text{2R}}}}{\text{  =  v}}_{\text{a}}^{\text{2}}{\text{ - }}\dfrac{{{\text{2GM}}}}{{{\text{6R}}}}$

${{\text{v}}_{\text{a}}}{\text{  =  }}\dfrac{{{{\text{v}}_{\text{p}}}}}{{\text{3}}}$

  ${\text{v}}_{\text{p}}^{\text{2}}{\text{ - v}}_{\text{a}}^{\text{2}}{\text{  =  }}\dfrac{{{\text{GM}}}}{{\text{R}}}{\text{ - }}\dfrac{{\text{1}}}{{\text{3}}}\dfrac{{{\text{GM}}}}{{\text{R}}}$

  ${\text{v}}_{\text{p}}^{\text{2}}{\text{ - }}{\left( {\dfrac{{{{\text{v}}_{\text{p}}}}}{{\text{3}}}} \right)^{\text{2}}}{\text{  =  }}\dfrac{{{\text{GM}}}}{{\text{R}}}\left[ {{\text{1 - }}\dfrac{{\text{1}}}{{\text{3}}}} \right]$

 ${\text{v}}_{\text{p}}^{\text{2}}\left[ {{\text{1 - }}\dfrac{{\text{1}}}{{\text{9}}}} \right]{\text{  =  }}\dfrac{{{\text{GM}}}}{{\text{R}}}{\text{ }\times{ }}\dfrac{{\text{2}}}{{\text{3}}}$

  ${\text{v}}_{\text{p}}^{\text{2}}\dfrac{{\text{8}}}{{\text{9}}}{\text{  =  }}\dfrac{{{\text{GM}}}}{{\text{R}}}{\text{ }\times{ }}\dfrac{{\text{2}}}{{\text{3}}}$

 ${\text{v}}_{\text{p}}^{\text{2}}{\text{  =  }}\dfrac{{{\text{GM}}}}{{\text{R}}}\dfrac{{\text{2}}}{{\text{3}}}{\text{ }\times{ }}\dfrac{{\text{9}}}{{\text{8}}}{\text{  =  }}\dfrac{{\text{3}}}{{\text{4}}}\dfrac{{{\text{GM}}}}{{\text{R}}}$

  ${{\text{v}}_{\text{p}}}{\text{  =  }}\sqrt {\dfrac{{\text{3}}}{{\text{4}}}\dfrac{{{\text{GM}}}}{{\text{R}}}} {\text{  =  }}\sqrt {\dfrac{{{\text{3 }\times{ 6}}{\text{.67 }\times{ 1}}{{\text{0}}^{{\text{ - 11}}}}{\text{ }\times{ 6 }\times{ 1}}{{\text{0}}^{{\text{24}}}}}}{{{\text{4 }\times{ 6}}{\text{.6 }\times{ 1}}{{\text{0}}^{\text{6}}}}}}$

  ${\text{ =  }}\sqrt {\dfrac{{{\text{9 }\times{ 667 }\times{ 1}}{{\text{0}}^{{\text{24 - 6 - 11 - 1}}}}}}{{{\text{128}}}}}$

  ${{\text{v}}_{\text{p}}}{\text{  =  }}\sqrt {\dfrac{{{\text{6003 }\times{ 1}}{{\text{0}}^{{\text{18 - 11 - 1}}}}}}{{{\text{128}}}}} {\text{  =  }}\sqrt {{\text{46}}{\text{.89 }\times{ 1}}{{\text{0}}^{\text{6}}}}$

  ${\text{ =  6}}{\text{.85 }\times{ 1}}{{\text{0}}^{\text{3}}}{\text{m/s  =  6}}{\text{.85km/s}}$

  ${{\text{v}}_{\text{a}}}{\text{  =  }}\dfrac{{{{\text{v}}_{\text{p}}}}}{{\text{3}}}{\text{  =  }}\dfrac{{{\text{6}}{\text{.85}}}}{{\text{3}}}{\text{  =  2}}{\text{.28km/s}}$

  ${{\text{v}}_{\text{c}}}{\text{  =  }}\sqrt {\dfrac{{{\text{GM}}}}{{\text{r}}}} {\text{  =  }}\sqrt {\dfrac{{{\text{6}}{\text{.67 }\times{ 1}}{{\text{0}}^{{\text{ - 11}}}}{\text{ }\times{ 6 }\times{ 1}}{{\text{0}}^{{\text{24}}}}}}{{{\text{6R}}}}}$

${\text{ =  }}\sqrt {\dfrac{{{\text{6}}{\text{.67 }\times{ 6 }\times{ 1}}{{\text{0}}^{{\text{24 - 11}}}}}}{{{\text{6 }\times{ 6}}{\text{.4 }\times{ 1}}{{\text{0}}^{\text{6}}}}}} {\text{  =  }}\sqrt {\dfrac{{{\text{667}}}}{{{\text{640}}}}{\text{ }\times{ 1}}{{\text{0}}^{{\text{13 - 6}}}}}$

${\text{ =  }}\sqrt {{\text{1}}{\text{.042 }\times{ 10 }\times{ 1}}{{\text{0}}^{\text{6}}}} {\text{  =  }}\sqrt {{\text{10}}{\text{.42 }\times{ 1}}{{\text{0}}^{\text{6}}}}$

${{\text{v}}_{\text{c}}}{\text{  =  3}}{\text{.23km/s}}$

Thus, to transfer a circular orbit at apogee to boost velocity is given by 

${{\text{v}}_{\text{0}}}{\text{ - }}{{\text{v}}_{\text{a}}}{\text{  =  (3}}{\text{.23 - 2}}{\text{.28)  =  0}}{\text{.95km/s}}$