NCERT Exemplar for Class 11 Chemistry Chapter-6 (Book Solutions)

Multiple Choice Questions (Type-I)

1.Thermodynamics is not concerned about ________. 

(i) energy changes involved in a chemical reaction. 

(ii) the extent to which a chemical reaction proceeds.

(iii) the rate at which a reaction proceeds. 

(iv) the feasibility of a chemical reaction. 

Ans: Thermodynamics is not concerned about how and at what rate these energy transformations are carried out but is based on initial and final states of a system undergoing the change. Laws of thermodynamics apply only when a system is in equilibrium or moves from one equilibrium state to another equilibrium state. Hence, option(iii) is the correct answer.

2.Which of the following statements is correct?

(i) The presence of reacting species in a covered beaker is an example of open system. 

(ii) There is an exchange of energy as well as matter between the system and the surroundings in a closed system. 

(iii) The presence of reactants in a closed vessel made up of copper is an example of a closed system. 

(iv) The presence of reactants in a thermos flask or any other closed insulated vessel is an example of a closed system. 

Ans: The presence of reactants in a closed vessel made of conducting material e.g., copper or steel is an example of a closed system. Hence, option(iii) is the correct answer.

3.The state of a gas can be described by quoting the relationship between _____.

(i) pressure, volume, temperature

(ii) temperature, amount, pressure

(iii) amount, volume, temperature 

(iv) pressure, volume, temperature, amount 

Ans: Variables like p, V, T are called state variables or state functions because their values depend only on the state of the system and not on how it is reached. Hence, option(i) is the correct answer.

4. The volume of gas is reduced to half from its original volume. The specific heat will _____. 

(i) reduce to half 

(ii) be doubled

(iii) remain constant 

(iv) increase four times 

Ans: Specific heat capacity is the quantity of heat required to raise the temperature of one unit mass of a substance by one degree Celsius (or one kelvin). That is why it is an intensive property which does not depend on mass. Hence, option(iii) is the correct answer.

5. During complete combustion of one mole of butane, 2658 kJ of heat is released. The thermochemical reaction for above change is 

\[\left( \mathbf{i} \right)\mathbf{ 2}{{\mathbf{C}}_{\mathbf{4}}}{{\mathbf{H}}_{\mathbf{10}}}\left( \mathbf{g} \right)\mathbf{ + 13}{{\mathbf{O}}_{\mathbf{2}}}\left( \mathbf{g} \right)\to \mathbf{8C}{{\mathbf{O}}_{\mathbf{2}}}\left( \mathbf{g} \right)\mathbf{ + 10}{{\mathbf{H}}_{\mathbf{2}}}\mathbf{O}\left( \mathbf{l} \right)\mathbf{ }{{\mathbf{\Delta }}_{\mathbf{c}}}\mathbf{H = 2658}\mathbf{.0 kJ mo}{{\mathbf{l}}^{\mathbf{1}}}\mathbf{ }\]

\[\left( \mathbf{ii} \right)\mathbf{ }{{\mathbf{C}}_{\mathbf{4}}}{{\mathbf{H}}_{\mathbf{10}}}\left( \mathbf{g} \right)\mathbf{ + }{}^{\mathbf{13}}/{}_{\mathbf{2}}{{\mathbf{O}}_{\mathbf{2}}}\mathbf{ }\left( \mathbf{g} \right)\mathbf{ }\to \mathbf{4C}{{\mathbf{O}}_{\mathbf{2}}}\left( \mathbf{g} \right)\mathbf{ + 5}{{\mathbf{H}}_{\mathbf{2}}}\mathbf{O }\left( \mathbf{g} \right)\mathbf{ }{{\mathbf{\Delta }}_{\mathbf{c}}}\mathbf{H= 1329}\mathbf{.0 kJ mo}{{\mathbf{l}}^{\mathbf{1}}}\]

\[\left( \mathbf{iii} \right)\mathbf{ }{{\mathbf{C}}_{\mathbf{4}}}{{\mathbf{H}}_{\mathbf{10}}}\left( \mathbf{g} \right)\mathbf{ + }{}^{\mathbf{13}}/{}_{\mathbf{2}}{{\mathbf{O}}_{\mathbf{2}}}\mathbf{ }\left( \mathbf{g} \right)\to \mathbf{4C}{{\mathbf{O}}_{\mathbf{2}}}\left( \mathbf{g} \right)\mathbf{ + 5}{{\mathbf{H}}_{\mathbf{2}}}\mathbf{O }\left( \mathbf{l} \right)\mathbf{ }{{\mathbf{\Delta }}_{\mathbf{c}}}\mathbf{H = 2658}\mathbf{.0 kJ mo}{{\mathbf{l}}^{\mathbf{1}}}\]

\[\left( \mathbf{iv} \right)\mathbf{ }{{\mathbf{C}}_{\mathbf{4}}}{{\mathbf{H}}_{\mathbf{10}}}\left( \mathbf{g} \right)\mathbf{ + }{}^{\mathbf{13}}/{}_{\mathbf{2}}{{\mathbf{O}}_{\mathbf{2}}}\mathbf{ }\left( \mathbf{g} \right)\to \mathbf{ 4C}{{\mathbf{O}}_{\mathbf{2}}}\left( \mathbf{g} \right)\mathbf{ + 5}{{\mathbf{H}}_{\mathbf{2}}}\mathbf{O }\left( \mathbf{l} \right)\mathbf{ }{{\mathbf{\Delta }}_{\mathbf{c}}}\mathbf{H= +2658}\mathbf{.0 kJ mo}{{\mathbf{l}}^{\mathbf{1}}}\]

Ans: Standard enthalpy of combustion is defined as the enthalpy change per mole (or per unit amount) of a substance when it undergoes combustion and all the reactants and products being in their standard states at the specified temperature. Hence, option(iii) is the correct answer.

6. \[{{\mathbf{\Delta }}_{\mathbf{f}}}{{\mathbf{U}}^{\mathbf{e}}}\] of formation of \[\mathbf{C}{{\mathbf{H}}_{\mathbf{4}}}\] (g) at certain temperature is –393 kJ mol–1. The value of \[{{\mathbf{\Delta }}_{\mathbf{f}}}{{\mathbf{H}}^{\mathbf{e}}}\] is 

(i) zero

(ii) < \[{{\mathbf{\Delta }}_{\mathbf{f}}}{{\mathbf{U}}^{\mathbf{e}}}\] 

(iii) > \[{{\mathbf{\Delta }}_{\mathbf{f}}}{{\mathbf{U}}^{\mathbf{e}}}\] 

(iv) equal to \[{{\mathbf{\Delta }}_{\mathbf{f}}}{{\mathbf{U}}^{\mathbf{e}}}\]

Ans: The balanced equation for the combustion of methane is: 

\[\text{C}{{\text{H}}_{\text{4}}}\left( \text{g} \right)\text{+2}{{\text{O}}_{\text{2}}}\left( \text{g} \right)\to \text{C}{{\text{O}}_{\text{2}}}\left( \text{g} \right)\text{+2}{{\text{H}}_{\text{2}}}\text{O}\left( \text{l} \right)\]

Therefore, \[\text{ }\!\!\Delta\!\!\text{ }{{\text{n}}_{\text{g}}}\] =1−3=−2

\[\text{ }\!\!\Delta\!\!\text{ }{{\text{H}}_{\text{o}}}\] = \[\text{ }\!\!\Delta\!\!\text{ }{{\text{U}}_{\text{o}}}\] + \[\text{ }\!\!\Delta\!\!\text{ }{{\text{n}}_{\text{g}}}\]​RT

\[\text{ }\!\!\Delta\!\!\text{ }{{\text{H}}_{\text{o}}}\]=−393−2RT

∴ \[\text{ }\!\!\Delta\!\!\text{ }{{\text{H}}_{\text{o}}}\]< \[\text{ }\!\!\Delta\!\!\text{ }{{\text{U}}_{\text{o}}}\]

Hence, option (ii) is the correct answer.

7. In an adiabatic process, no transfer of heat takes place between system and surroundings. Choose the correct option for free expansion of an ideal gas under adiabatic condition from the following. 

(i) q = 0, ∆T ≠ 0, w = 0 

(ii) q ≠ 0, ∆T = 0, w = 0 

(iii) q = 0, ∆T = 0, w = 0 

(iv) q = 0, ∆T < 0, w ≠ 0 

Ans: In free expansion, w=0 because volume is constant, as the process is adiabatic q = 0 and from first law of thermodynamics.

\[\text{ }\!\!\Delta\!\!\text{ U=q+w}\]

This means that internal energy remains constant.

Hence, option(iii) is the correct answer.

8. The pressure-volume work for an ideal gas can be calculated by using the expression \[\mathbf{w=-}\int\limits_{{{\mathbf{V}}_{\mathbf{i}}}}^{{{\mathbf{V}}_{\mathbf{f}}}}{{{\mathbf{P}}_{\mathbf{ex}}}}\mathbf{dV}\]

The work can also be calculated from the pV plot by using the area under the curve within the specified limits. When an ideal gas is compressed 

(a) reversibly or (b) irreversibly from volume \[{{\mathbf{V}}_{\mathbf{i}}}\] to \[{{\mathbf{V}}_{\mathbf{f}}}\]. 

choose the correct option. 

(i) w (reversible) = w (irreversible) 

(ii) w (reversible) < w (irreversible) 

(iii) w (reversible) > w (irreversible) 

(iv) w (reversible) = w (irreversible) + \[{{\mathbf{P}}_{\mathbf{ex}}}\] ∆V

Ans: As the area under the curve is always more in irreversible compression and this can be explained by the below curves- 

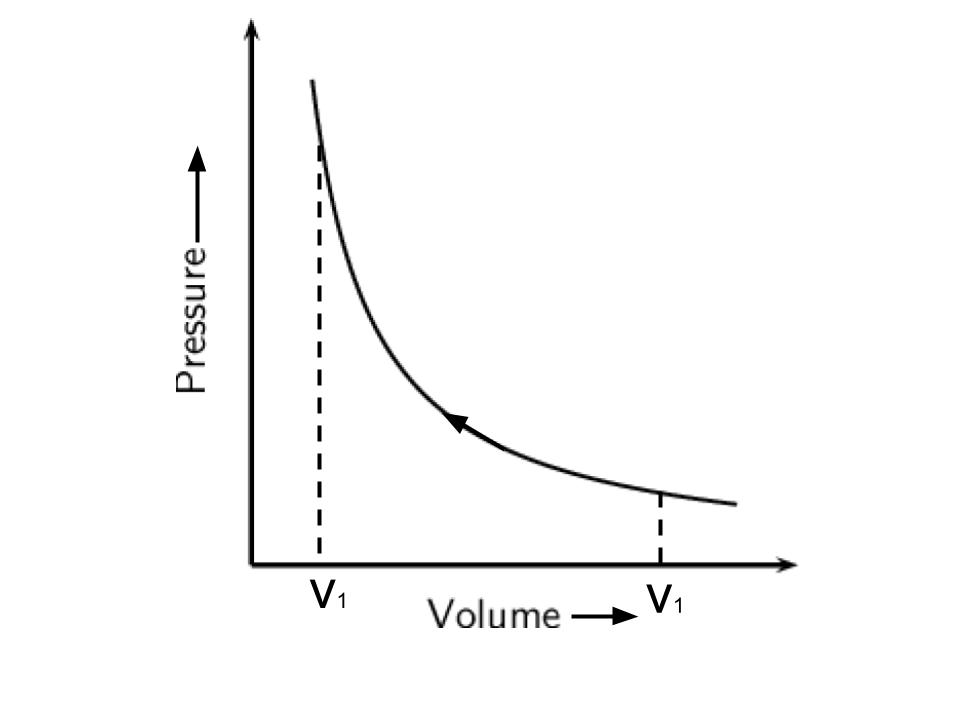
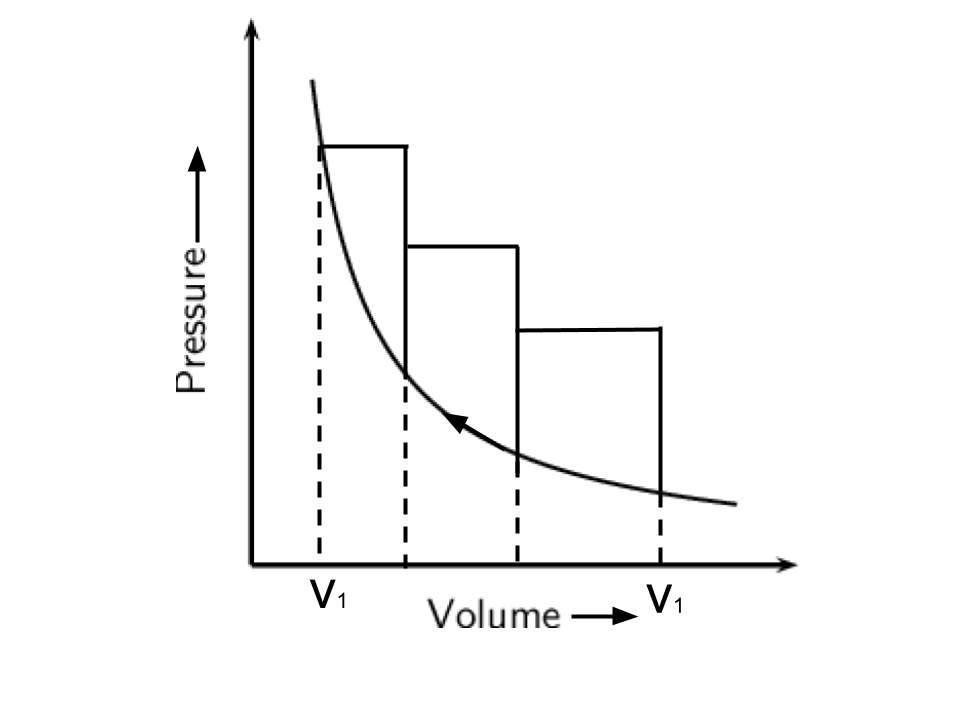
Hence, option(ii) is the correct answer.

9. The entropy change can be calculated by using the expression \[\mathbf{\Delta S =}{{\mathbf{q}}_{\mathbf{rev}}}\mathbf{T}\] . When water freezes in a glass beaker, choose the correct statement amongst the following : 

(i) ∆S (system) decreases but ∆S (surroundings) remains the same. 

(ii) ∆S (system) increases but ∆S (surroundings) decreases.

(iii) ∆S (system) decreases but ∆S (surroundings) increases.

(iv) ∆S (system) decreases and ∆S (surroundings) also decreases.

Ans: (iii) ∆S (system) decreases but ∆S (surroundings) increases.

10. On the basis of thermochemical equations (a), (b) and (c), find out which of the algebraic relationships given in options (i) to (iv) is correct. 

\[\left( \mathbf{a} \right)\mathbf{ C}{{\mathbf{ }}_{\left( \mathbf{graphite} \right)\mathbf{ }}}\mathbf{+ }{{\mathbf{O}}_{\mathbf{2 }}}\left( \mathbf{g} \right)\mathbf{ }\to \mathbf{C}{{\mathbf{O}}_{\mathbf{2}}}\mathbf{ }\left( \mathbf{g} \right)\mathbf{ ; }{{\mathbf{\Delta }}_{\mathbf{r}}}\mathbf{H = x kJ mo}{{\mathbf{l}}^{\mathbf{1}}}\]

\[\left( \mathbf{b} \right)\mathbf{ C}{{\mathbf{ }}_{\left( \mathbf{graphite} \right)}}\mathbf{ + }\frac{\mathbf{1}}{\mathbf{2}}{{\mathbf{O}}_{\mathbf{2}}}\mathbf{ }\left( \mathbf{g} \right)\to \mathbf{CO }\left( \mathbf{g} \right)\mathbf{ ; }{{\mathbf{\Delta }}_{\mathbf{r}}}\mathbf{H  = y kJ mo}{{\mathbf{l}}^{\mathbf{1}}}\]

\[\left( \mathbf{c} \right)\mathbf{ CO }\left( \mathbf{g} \right)\mathbf{ + }\frac{\mathbf{1}}{\mathbf{2}}\mathbf{ }{{\mathbf{O}}_{\mathbf{2}}}\mathbf{ }\left( \mathbf{g} \right)\to \mathbf{C}{{\mathbf{O}}_{\mathbf{2}}}\mathbf{ }\left( \mathbf{g} \right)\mathbf{ ; }{{\mathbf{\Delta }}_{\mathbf{r}}}\mathbf{H = z kJ mo}{{\mathbf{l}}^{\mathbf{1}}}\]

(i) z = x + y

(ii) x = y – z

(iii) x = y + z 

(iv) y = 2z – x

Ans:  When we add equations (b) and (c) we will get equation(a) hence, Algebraic sum of y and z will give x, x =y + z. Hence, option(iii) is the correct answer.

11. Consider the reactions given below. On the basis of these reactions find out which of the algebric relations given in options (i) to (iv) is correct?

\[\begin{array}{*{35}{l}}   \left( \mathbf{a} \right)\mathbf{ C }\left( \mathbf{g} \right)\mathbf{ + 4 H }\left( \mathbf{g} \right)\mathbf{ }\to \mathbf{ C}{{\mathbf{H}}_{\mathbf{4}}}\mathbf{ }\left( \mathbf{g} \right)\mathbf{;}{{\mathbf{\Delta }}_{\mathbf{r }}}\mathbf{H = x kJ mo}{{\mathbf{l}}^{\mathbf{1}}}  \\   \left( \mathbf{b} \right)\mathbf{ C}{{\mathbf{ }}_{\left( \mathbf{graphite,s} \right)}}\mathbf{ + 2}{{\mathbf{H}}_{\mathbf{2}}}\mathbf{ }\left( \mathbf{g} \right)\to \mathbf{ C}{{\mathbf{H}}_{\mathbf{4}}}\mathbf{ }\left( \mathbf{g} \right)\mathbf{; }{{\mathbf{\Delta }}_{\mathbf{r }}}\mathbf{H = y kJ mo}{{\mathbf{l}}^{\mathbf{1}}}  \\\end{array}\] 

(i) x = y 

(ii) x = 2y

(iii) x > y

(iv) x < y

Ans: Same bonds are formed in reaction (a) and (b) but bonds between the reactant molecules are broken only in reaction (b). Hence option(iii) is the correct answer.

12. The enthalpies of elements in their standard states are taken as zero. The enthalpy of formation of a compound- 

(i) is always negative

(ii) is always positive 

(iii) may be positive or negative 

(iv) is never negative

Ans: The enthalpies of elements in their standard states are taken as zero. The enthalpy of formation of a compound as the reaction could be exothermic or endothermic. Hence, option(iii) is the correct answer.

13. Enthalpy of sublimation of a substance is equal to

(i) enthalpy of fusion + enthalpy of vaporisation 

(ii) enthalpy of fusion

(iii) enthalpy of vaporisation 

(iv) twice the enthalpy of vaporisation

Ans: Enthalpy of sublimation can be shown as

 Solid \[\to \] Liquid \[\to \]Vapour

Hence, Enthalpy of sublimation of a substance is equal to enthalpy of fusion + enthalpy of vaporisation. Therefore, option(i) is the correct answer. 

14. Which of the following is not correct?

(i) ∆G is zero for a reversible reaction

(ii) ∆G is positive for a spontaneous reaction

(iii) ∆G is negative for a spontaneous reaction

(iv) ∆G is positive for a non-spontaneous reaction 

Ans: \[\text{ }\!\!\Delta\!\!\text{ G}\] positive for a spontaneous reaction. Hence, option(ii) is the correct answer.

Multiple Choice Questions (Type-II) 

In the following questions two or more options may be correct.

15.Thermodynamics mainly deals with

(i) interrelation of various forms of energy and their transformation from one form to another. 

(ii) energy changes in the processes which depend only on initial and final states of the microscopic systems containing a few molecules. 

(iii) how and at what rate these energy transformations are carried out. 

(iv) the system in equilibrium state or moving from one equilibrium state to another equilibrium state. 

Ans: The laws of thermodynamics deal with energy changes of macroscopic systems involving a large number of molecules rather than microscopic systems containing a few molecules. Laws of thermodynamics apply only when a system is in equilibrium or moves from one equilibrium state to another equilibrium state. Hence, option (i) an (iv) is the correct answer.

16. In an exothermic reaction, heat is evolved, and system loses heat to the surroundings. For such system 

(i) \[{{\mathbf{q}}_{\mathbf{p}}}\] will be negative 

(ii) \[{{\mathbf{\Delta }}_{\mathbf{r}}}\mathbf{H }\] will be negative

(iii) \[{{\mathbf{q}}_{\mathbf{p}}}\] will be positive 

(iv) \[{{\mathbf{\Delta }}_{\mathbf{r}}}\mathbf{H }\] will be positive 

Ans: In an exothermic reaction, heat is evolved, and system loses heat to the surroundings. Therefore, \[{{\text{q}}_{\text{p}}}\] will be negative and \[{{\text{ }\!\!\Delta\!\!\text{ }}_{\text{r}}}\text{H }\] will also be negative. Hence, option(i) and (ii) is the correct answer.

17. The spontaneity means, having the potential to proceed without the assistance of external agency. The processes which occur spontaneously are

(i) flow of heat from colder to warmer body.

(ii) gas in a container contracting into one comer.

(iii) gas expanding to fill the available volume. 

(iv) burning carbon in oxygen to give carbon dioxide. 

Ans: Gas expands to fill the available space spontaneously and burning of carbon-to-carbon dioxide is spontaneous. Hence, option(iii) and (iv) is the correct answer.

18. For an ideal gas, the work of reversible expansion under isothermal condition can be calculated by using the expression \[\mathbf{w =  nRT ln }\frac{{{\mathbf{V}}_{\mathbf{f}}}}{{{\mathbf{V}}_{\mathbf{i}}}}\] .A sample containing 1.0 mol of an ideal gas is expanded isothermally and reversibly to ten times of its original volume, in two separate experiments. The expansion is carried out at 300 K and at 600 K respectively. Choose the correct option. 

(i) Work done at 600 K is 20 times the work done at 300 K.

(ii) Work done at 300 K is twice the work done at 600 K.

(iii) Work done at 600 K is twice the work done at 300 K.

(iv) ∆U = 0 in both cases. 

Ans: For isothermal reversible change, we know

\[\text{q=-w=nRTIn}\frac{{{\text{V}}_{\text{f}}}}{{{\text{V}}_{\text{i}}}}\text{=2}\text{.303nRTlog}\frac{{{\text{V}}_{\text{f}}}}{{{\text{V}}_{\text{i}}}}\]

\[\frac{\begin{align}  &  \\  & {{\text{W}}_{\text{600K}}} \\ \end{align}}{{{\text{W}}_{\text{300K}}}}\text{=}\frac{\text{1 }\!\!\times\!\!\text{ R }\!\!\times\!\!\text{ 300KIn}\frac{\text{1}}{\text{10}}}{\text{1 }\!\!\times\!\!\text{ R }\!\!\times\!\!\text{ 600KIn}\frac{\text{1}}{\text{10}}}\text{=}\frac{\text{600}}{\text{300}}\text{=2}\]

For isothermal expansion of ideal gases, ΔU=0

Since temperature is constant this means there is no change in internal energy.
Therefore, ΔU=0. Hence, option(iii) and (iv) is the correct answer.

19. Consider the following reaction between zinc and oxygen and choose the correct options out of the options given below:

\[\mathbf{2}\text{ }\mathbf{Zn}\text{ }\left( \mathbf{s} \right)+{{\mathbf{O}}_{\mathbf{2}}}\text{ }\left( \mathbf{g} \right)\text{ }\to \mathbf{2}\text{ }\mathbf{ZnO}\text{ }\left( \mathbf{s} \right)\text{ };\text{ }\Delta \mathbf{H}=\text{ }\mathbf{693}.\mathbf{8}\text{ }\mathbf{kJ}\text{ }\mathbf{mo}{{\mathbf{l}}^{\mathbf{1}}}\] 

(i) The enthalpy of two moles of ZnO is less than the total enthalpy of two moles of Zn and one mole of oxygen by 693.8 kJ.

(ii) The enthalpy of two moles of ZnO is more than the total enthalpy of two moles of Zn and one mole of oxygen by 693.8 kJ.

(iii) 693.8 kJ mol–1 energy is evolved in the reaction. 

(iv) 693.8 kJ mol–1 energy is absorbed in the reaction. 

Ans: As we know from thermodynamics, 

\[{{\text{ }\!\!\Delta\!\!\text{ }}_{\text{r}}}{{\text{H}}^{\text{o}}}{{\text{=}}_{\text{i}}}\sum{{{\text{a}}_{\text{i}}}}{{\text{ }\!\!\Delta\!\!\text{ }}_{\text{f}}}{{\text{H}}^{\odot }}\left( \text{products} \right)\text{-}\sum{{{\text{a}}_{\text{i}}}}{{\text{b}}_{\text{i}}}{{\text{ }\!\!\Delta\!\!\text{ }}_{\text{f}}}{{\text{H}}^{\odot }}\left( \text{reactants} \right)\]
Since, the above reaction is an exothermic reaction, the enthalpy of reactant is more than the enthalpy of product. Hence, option(i) and (iii) is the correct answer.

III. Short Answer Type 

20. 18.0 g of water completely vaporises at \[\mathbf{10}{{\mathbf{0}}^{\mathbf{\bullet }}}\mathbf{C}\] and 1 bar pressure and the enthalpy change in the process is 40.79 kJ \[\mathbf{Mo}{{\mathbf{l}}^{\mathbf{-1}}}\]. What will be the enthalpy change for vaporising two moles of water under the same conditions? What is the standard enthalpy of vaporisation for water?

Ans: Enthalpy of a reaction is defined as the energy change per mole for the process. Therefore, 

18 g of \[{{\text{H}}_{\text{2}}}\text{O}\]= 1 mole (\[\text{ }\!\!\Delta\!\!\text{ }{{\text{H}}_{\text{Vap}}}\] = 40.79 kJ \[\text{Mo}{{\text{l}}^{\text{-1}}}\]) 

Enthalpy change for vaporising 2 moles of \[{{\text{H}}_{\text{2}}}\text{O}\] = 2 x 40.79 = 81.58 kJ

\[\text{ }\!\!\Delta\!\!\text{ }{{\text{H}}_{\text{Vap}}}\] = 40.79 kJ \[\text{Mo}{{\text{l}}^{\text{-1}}}\].

21. One mole of acetone requires less heat to vapourise than 1 mol of water. Which of the two liquids has higher enthalpy of vaporization?

Ans:  Due to weak force of attraction between molecules, acetone requires less heat to vaporise. Hence, water has higher enthalpy of vaporization.

22. Standard molar enthalpy of formation, $\Delta $fH- is just a special case of enthalpy of reaction, $\Delta $rH- Is the $\Delta $rH- forhe following reaction same as $\Delta $fH-? Give reason for your answer.

CaO(s)+CO2(g)$\to $CaCO3(s) $\Delta $fH-= -178.3KJ/mol

Ans: Standard molar enthalpy of formation,rH1- is just a special case of fH2-, where

one mole of a compound is formed from its constituent elements. In the above equation, enthalpy of formation and enthalpy of reaction is not the same.

23.The value of $\Delta {{H}^{\Theta }}$ for NH3 is – 91.8 kJ mol-1. Calculate the enthalpy change for the following reaction :

2NH3(g) $\to $N2(g) + 3H2(g)

Ans: The enthalpy change for the given reaction can be calculated as: -

N2(g) + 3H2(g)$\to $2NH3 (g)

$\Delta $fH=-91.8kg/mol

The enthalpy of the reaction is +91.8 kg/mol. This happens as with the reversal of reaction, the value of $\Delta $fH also gets reversed.

24. Enthalpy is an extensive property. In general, if enthalpy of an overall reaction A→B along one route is $\Delta $rH and $\Delta $rH1, $\Delta $rH2, $\Delta $rH3……represent enthalpies of intermediate reactions leading to product B. What will be the relation between $\Delta $rH for overall reaction and$\Delta $rH1, $\Delta $rH2, $\Delta $rH3 etc for intermediate reactions.

Ans: According to Hess’s law, $\Delta $rH = $\Delta $rH1+ $\Delta $rH2+$\Delta $rH3

This is so because during the reaction A$\to $ B, B’s formation undergoes various intermediate reactions, with the overall value of the enthalpy being $\Delta $rH.

25. The enthalpy of atomisation for the reaction CH4(g)$\to $C(g) + 4H (g)  is 1665kJ mol-1. What is the bond energy of C-H bond?

Ans: The reaction presented in the question is

CH4(g)$\to $C(g) + 4H (g)

Now, $\Delta $aH = 1665  kJ mol-1

The mean bond enthalpy of the C-H bond should be used here. For the atomisation of 4 moles of C-H bonds, the value is 1665 kJ/mol-1. So, per mole energy = 1665/4 = 416.2 kJ / mol-1.

26. Use the following data to calculate $\Delta $ latticeH$\ominus $for NaBr.

$\Delta $sub H$\ominus $for sodium metal = 108.4 kJ mol–1

Ionization enthalpy of sodium = 496 kJ mol-1

Electron gain enthalpy of bromine = – 325 kJ mol-1

Bond dissociation enthalpy of bromine = 192 kJ mol-1

$\Delta $fH$\ominus $for NaBr (s) = – 360.1 kJ mol-1

Ans: In order to calculate the lattice enthalpy of NaBr,

(i)Na(s) $\to $Na(g) ;$\Delta $ subH$\circ $=108.4 kJ mol-1

(ii) Na$\to $Na+ + e-   ; $\Delta $iH$\circ $ = 496kJ mol-1

(iii) $\frac{~~~1~}{2}$Br2$\to $ Br, $\frac{~~1~~}{2}\Delta $ dissH$\circ $=96kJ mol-1

(iv) Br+e-$\to $Br-;  $\Delta $ egH$\circ $= - 325 kJmol-1

$\Delta $fH$\circ $= $\Delta $ subH$\circ $+ $\frac{~~1~~}{2}\Delta $ dissH$\circ $+$\Delta $iH$\circ $+ $\Delta $ egH$\circ $+ $\Delta $ latticeH$\circ $

= -360.1 -108.4-96-496+325 = -735.5KJ mol-1

27. Given that ΔH= 0 for mixing of two gases. Explain whether the diffusion of these gases into each other in a closed container is a spontaneous process or not?

Ans: It is a spontaneous process. Although enthalpy change is zero, randomness or disorder (ΔS) increases and ΔS is positive. Therefore, in the equation, ΔG = ΔH – TΔS, the term TΔS will be negative. Hence ΔG will be negative.

28. Heat has a randomising influence on a system and temperature is the measure of average chaotic motion of particles in the system. Write the mathematical relation which relates these three parameters.

Ans: Heat has a randomising influence on a system and temperature is the measure of average chaotic motion of particles in the system. The mathematical relation which relates these three parameters is ΔS = qrev/ T

Here, ΔS = change in entropy                                                  ^

qrcv = heat of reversible reaction ‘

T = temperature

29. Increase in enthalpy of the surroundings is equal to decrease in enthalpy of the system. Will the temperature of the system and surroundings be the same when they are in thermal equilibrium?

Ans: Yes, when the system and the surroundings are in thermal equilibrium, their temperatures are the same.

30. At 298 K, Kp for the reaction N204(g)⇌ 2N02(g) is 0.98. Predict whether the reaction is spontaneous or not.

Ans: ΔrG° = -RT ln Kp

= -RT ln (0.98)

Since In (0.98) is negative

.’. ΔrG° is positive the reaction is non spontaneous

31. A sample of 1.0 mol of a monatomic ideal gas is taken through a cyclic process of expansion and compression as shown in the figure. What will be the value of ΔHfor the cycle as a whole?

Ans: 

For a cyclic process, ΔH = 0

32. The standard molar entropy of H2O(l) is 70 J K-1 mol-1. Will the standard molar entropy H2O(s) be more, or less than 70 J K ^-1 mol^-1?

Ans: The standard molar entropy of H₂0 (1) is 70 J K^-1 mol-1. The solid form of H₂0 is ice. In ice, molecules of H₂0 are less random than in liquid water. Thus, molar entropy of H₂0 (s) < molar entropy of H₂0 (1). The standard molar entropy of H₂0 (s) is less than 70 J K 1 mol^-1.

33. Identify the state functions and path functions out of the following: enthalpy, entropy, heat, temperature, work, free energy.

Ans: State functions: Enthalpy, entropy, temperature, free energy Path functions: Heat, work

34. The molar enthalpy of vaporization of acetone is less than that of water. Why?

Ans:  Molar enthalpy of vaporization is more for water due to hydrogen bonding between water molecules.

Q35. Which quantity out of ΔrG and ΔrG° will be zero at equilibrium?

Ans:  Gibbs energy for a reaction in which all reactants and products are in standard state. ΔrG° is related to the equilibrium constant of the reaction as follows

ΔrG = ArG° + RT In K

At equilibrium, 0 = ΔrG° + RT In A– ({ΔrG = 0) or    ΔrG° =-RT lnK

ΔrG° = 0 when K= 1

For all other values of K, ArG° will be non-zero.

36. Predict the change in internal energy for an isolated system at constant volume.

Ans: For an isolated system w = 0, q = 0

Since ΔU= q + w = 0 + 0 = 0, ΔU= 0

37. Although heat is a path function, heat absorbed by the system under certain specific conditions is independent of path. What are those conditions? Explain.

Ans : At constant volume

q = ΔU + (-w)

-w = pΔ q = AU + pΔV

ΔV = 0 (at constant volume)

Hence, qv = ΔU + 0 = ΔU= change in internal energy at constant pressure, qp = AU + pΔV

Since ΔU + pΔV=ΔH

=> qp = ΔH change in enthalpy

Hence, at constant volume and at constant pressure, heat change is a state function because it is equal to ΔU and ΔH respectively which are state functions.

38. Expansion of a gas in vacuum is called free expansion. Calculate the work done and the change in internal energy when 1 litre of ideal gas expands isothermally into vacuum until its total volume is 5 litre.

Ans: During free expansion, external pressure is zero, so Work done, w = -pextΔV

= -0(5 – 1) = 0

Since the gas is expanding isothermally, therefore, q = 0

ΔU = q + w =0+0=0

39. Heat capacity (CP) is an extensive property but specific heat (c) is an intensive property. What will be the relation between Cp and c for 1 mol of water?

Ans: For water, molar heat capacity = 18 x Specific heat or Cp = 18 x c

But, specific heat,

C = 4.18 J g^-1 K^-1 Heat capacity,

Cp = 18 x 4.18 JK 1 = 75.24 JK^-1

40. The difference between Cp and Cv can be derived using the empirical relation H = U + pV. Calculate the difference between Cp and Cv for 10 moles of an ideal gas.

Ans: Given that, Cv = heat capacity at constant volume,

Cp = heat capacity at constant pressure

 Difference between Cp and Cv is equal to gas constant (R).

.’. Cp – Cv = nR                                (where, n = no. of moles)

= 10 x 8.314 = 83.14J

41. If the combustion of 1 g of graphite produces 20.7 kJ of heat, what will be the molar enthalpy change? Give the significance of the sign also.

Ans: Molar enthalpy change for graphite (ΔH)

= enthalpy change for 1 g x molar mass of C = -20.7×12 = -2.48 x 102 kJ mol-1

Since the sign of ΔH = -ve, it is an exothermic reaction.

42. The net enthalpy change of a reaction is the amount of energy required to break all the bonds in reactant molecules minus the amount of energy required to form all the bonds in the product molecules. What will be the enthalpy change for the following reaction?

H2(g) + Br2(g)→2HBr(g)

Given that the bond energy of H2, Br2 and HBr is 4.35 kJ mol-1,192 kJ mol-1 and 368 kJ mol -1 respectively.

Ans: $\Delta $rH$\circ $=$\Sigma $B.E(reactant)-$\Sigma $B.E(product)

 =B.E.H2 + BEBR2 -2 $\times $B.E>HBr

= 435+192-2($\times $368)

= 109KJmol-1

43. The enthalpy of vaporization of CCl4 is 30.5 kJ mol–1 . Calculate the heat required for the  vaporization of 284 g of CCl4 at constant pressure. (Molar mass of CCl4 = 154 g mol–1).

Ans: As per the information provided in the question, for one mole of CCl4(154 g), the heat of vaporisation required is 30.5 kJ/mol .

Hence for the vaporisation of 284 g of CCl4, we require:

$\frac{~~~284~~~}{154}\times $30.5

=56.2 kJ

44. The enthalpy of reaction for the reaction:

2H2 (g) + O2(g) $\to $2H2O(l) $\Delta $ rH$\ominus $= - 572 kJmol-1. What will be the standard enthalpy of formation of H2O(l) ?

Ans: Standard molar enthalpy of formation is the enthalpy change for the formation of one mole of a compound from its most stable states or reference states. As per the given information in the question, the standard enthalpy for the given equation is – 572 kJ mol^–1

Now the enthalpy of formation for \[H_{2}O\] will be half the enthalpy of the value in the given equation. So, now we can calculate that:

$\Delta $fH=$\frac{~~~1~~}{2}\times \Delta $yH= $\frac{~~~572~~}{2}$=-286KJmol-1

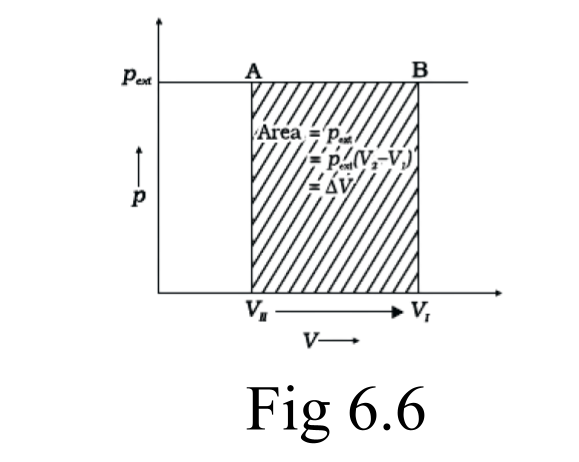
45. What will be the work done on an ideal gas enclosed in a cylinder, when it is compressed by a constant external pressure, pext in a single step as shown in Fig. 6.2. Explain graphically.

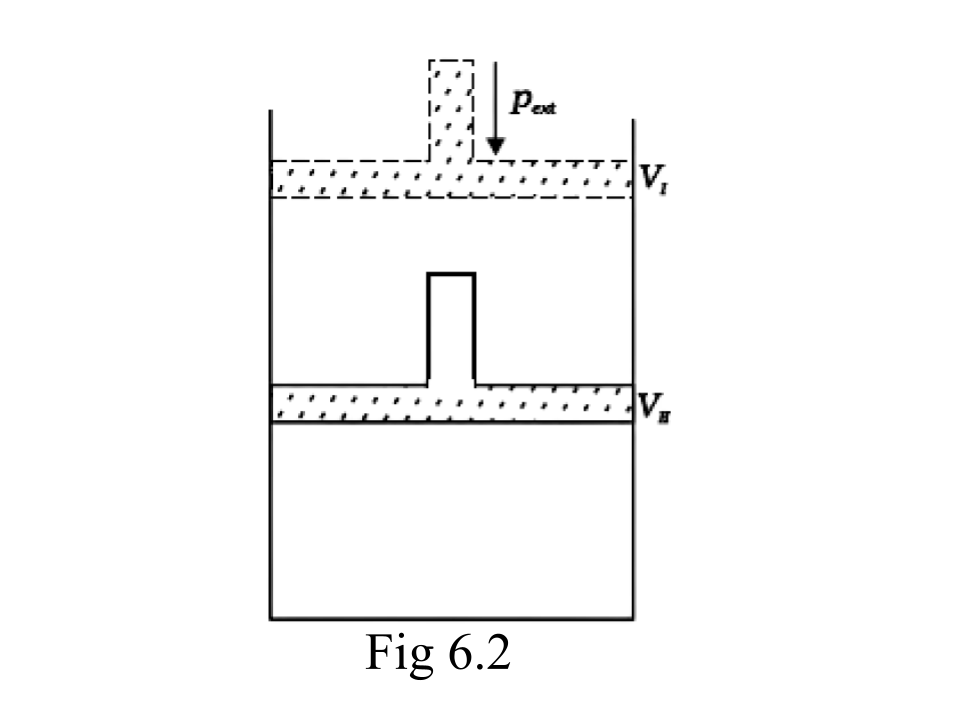
Ans: Assumption: Cylinder is filled with one mole gas, and the piston is frictionless. Let the pressure of gas inside be p and the volume of gas be V_{I}.

Piston is moved towards the inside to make the external pressure (P_{ext}) equal to p. Now, let us assume that this change takes place in a single step, hence, V is the final volume. The work done by the piston is depicted in the graph shown below by shading the area.

Pext$\Delta $V= AV1$\times $(V1-V2)

46. How will you calculate work done on an ideal gas in a compression, when change in pressure is carried out in infinite steps?

Ans: When a process can be reversed by bringing an extremely small change in it, we call it a reversible process. The pressure-volume graph can be used to calculate the work done. The pressure is not constant, and changes in infinitesimal amounts as compression happens from initial volume Vi to the final volume Vf. The below graph depicts the work done with the shaded area.

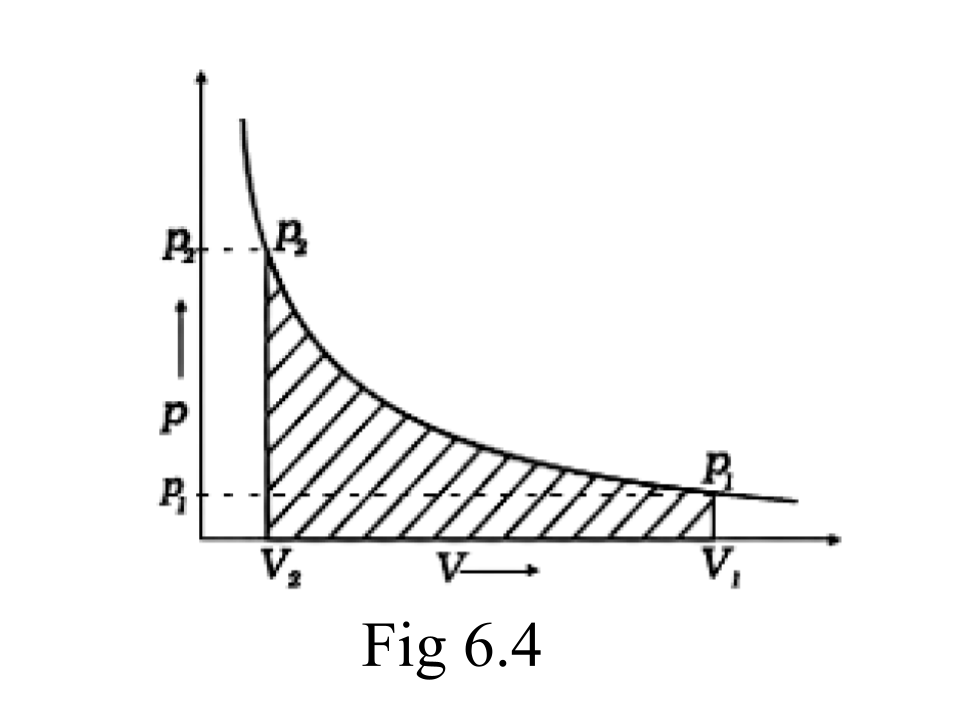
47.  Represent the potential energy/enthalpy change in the following processes graphically.

(a) Throwing a stone from the ground to roof.

(b) $\frac{~~1~~}{2}$H2(g)+ $\frac{~~1~~}{2}$Cl2(g)$\to $HCl (g) $\Delta $rH$\Theta $=-92.32kJmol-1

In which of the processes potential energy/enthalpy change is a contributing factor to the spontaneity?

Ans:

(a) Throwing a stone from ground to roof

b) the reaction involved is a process where the energy decreases after the reaction. It can be represented as:

In process b), potential energy/enthalpy change is a contributing factor to the spontaneity.

48. Enthalpy diagram for a particular reaction is given in Fig. 6.3. Is it possible to decide spontaneity of a reaction from a given diagram? Explain.

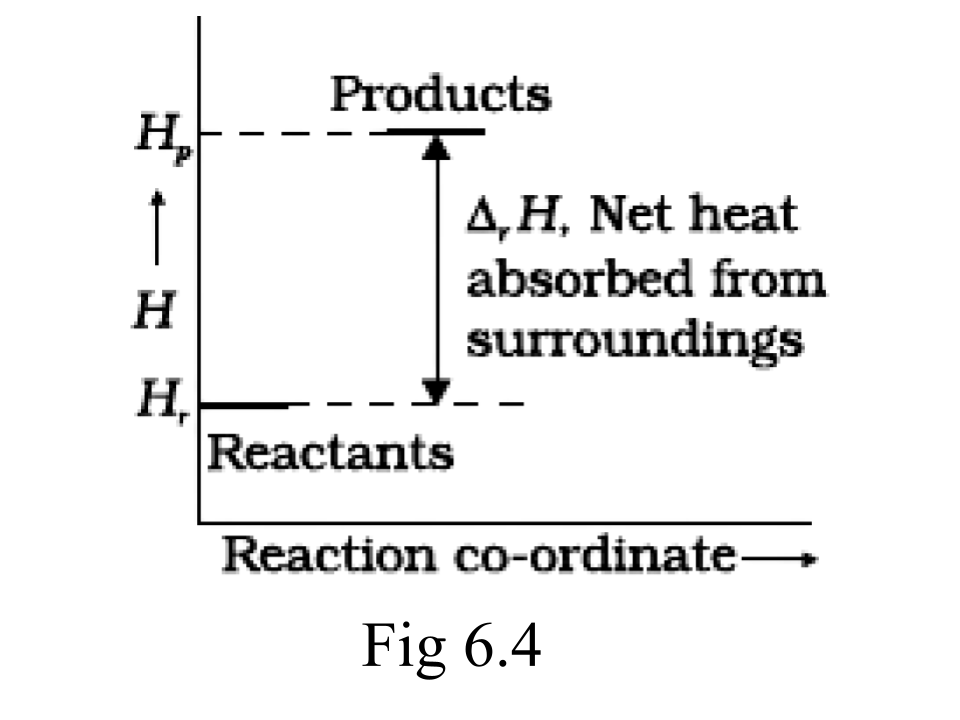
Ans: No, for the state of spontaneity, the enthalpy change is not the only criteria. Entropy also needs to be taken into account here.

49. 1.0 mol of a monatomic ideal gas is expanded from state (1) to state (2) as shown in figure. Calculate the work done for the expansion of gas from state (1) to state (2) at 298 K.

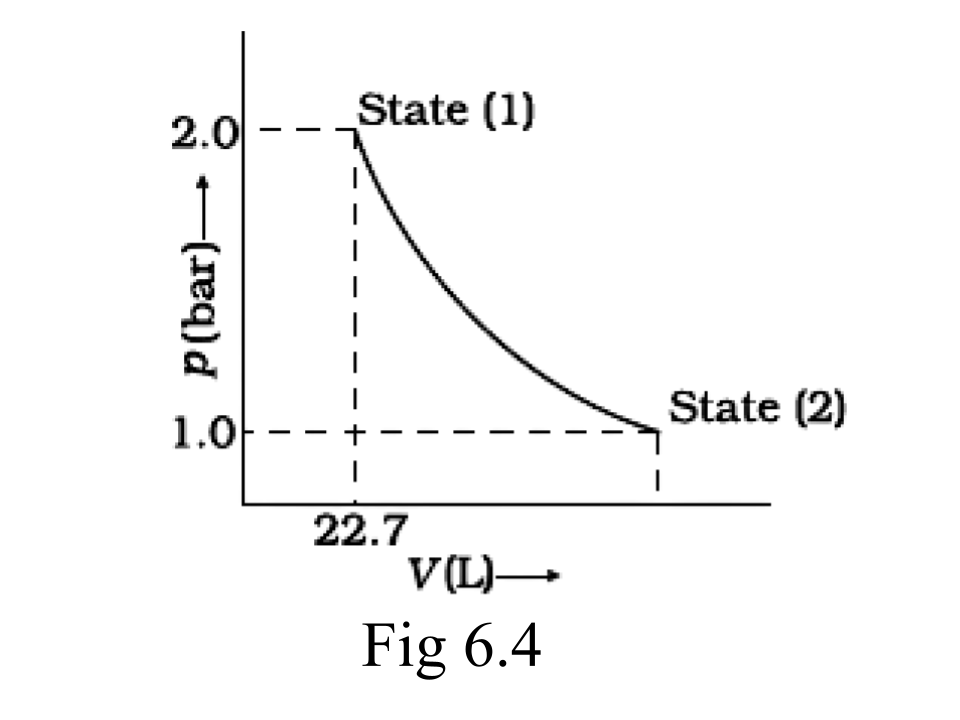
Ans: We can conclude from the figure that this change is a reversible change.

Now,

W= -2.303 $\times $nRT log$\frac{~~~p1~~}{p2}$

=-2.303 $\times $8.314$\times $1$\times $298$\times $log2

= -2.303 $\times $8.314$\times $298$\times $0.3010J

=-1717.46J

50. An ideal gas is allowed to expand against a constant pressure of 2 bar from 10 L to 50 L in one step. Calculate the amount of work done by the gas. If the same expansion were carried out reversibly, will the work done be higher or lower than the earlier case?

(Given that 1 L bar = 100 J)

Ans: We know that the amount of work done =-pext$\Delta $V

On substituting the values in the formula, we get,

-2bar$\times $(50-10)L=-80Lbar

According to the described problem,1LBar = 100J

Therefore, -80 Lbar=(-80$\times $100)=-8000J

=-8kJ, which is the amount of work done

The significance of the negative sign states that the work is done on the surroundings of the system. In the case of reversible expansion, the work done will be more.

In the following questions, more than one correlation is possible between options of both columns.

51.Match the followings:

Ans: 

(i)- (e)

(ii)- (d)

(iii)- (f)

(iv)- (a)

(v)- (g)

(k)- (L)

(vi)- (b)

(vii)- (c)

(viii)- (j)

(ix)- (h)

(x)- (i)

(xi)- (a), (l), (m)

(xii)- (g), (k)

52. Match the following processes with entropy change:

Ans: 

(i) (b)

(ii) (c)

(iii) (a)

53. Match the following parameters with description for spontaneity:

Ans: (i)- (c)

(ii)- (a)

(iii)- (b)

54. Match the following:

Ans: 

(i)- (b), (d)

(ii)- (b)

(iii)- (c)

(iv)- (a)

In the following questions a statement of Assertion (A) followed by a statement of reason (R) is given. Choose the correct option out of the choices given below each question.

55. Assertion (A): Combustion of all organic compounds is an exothermic reaction.

Reason (R): The enthalpies of all elements in their standard state are zero.

(i) Both A and R are true and R is the correct explanation of A.

(ii) Both A and R are true but R is not the correct explanation of A.

(iii) A is true but R is false.

(iv) A is false but R is true.

Ans: (ii)

Explanation: The enthalpy of the reactants is always greater than the enthalpy of the product in a combustion reaction.

56. Assertion (A): Spontaneous process is an irreversible process and may be reversed by some external agency.

Reason (R): Decrease in enthalpy is a contributory factor for spontaneity.

(i) Both  A and R are true and R is the correct explanation of A.

(ii) Both A and R is true but R is not the correct explanation of A.

(iii) A is true but R is false.

(iv) A is false but R is true.

Ans: (ii)

Explanation: The energy factor for a spontaneous process should be favourable (i.e., -ve) and the randomness should be positive.

57. Assertion (A): A liquid crystallises into a solid and is accompanied by decrease in entropy.

Reason (R): In  crystals, molecules organise in an ordered manner.

(i) Both A and R are true and R is the correct explanation of A.

(ii) Both A and R are true but R is not the correct explanation of A.

(iii) A is true but R is false.

(iv) A is false but R is true.

Ans:(i)

Explanation: The entropy of a liquid reduces as it crystallises. Because the molecules are more organised in crystalline form.

Long Answer Type

58. Derive the relationship between H and U for an ideal gas. Explain each term involved in the equation.

Ans: We know that the change in internal energy equals the heat absorbed at constant volume, i.e., U= qV.m. However, the majority of chemical reactions are carried out in flasks or test tubes under constant atmospheric pressure U= qp -PV under constant pressure, where qp is the heat absorbed by the system and -PV is the expansion work done by the system.

Let's call the beginning state with subscript 1 and the end state with subscript 2.

The above equation can be rewritten as

U2-U1= P(V2-V1)

On rearranging, we get

qp= (U2+pV2) - (U1 + pV1)...........(1)

Now, we can define another thermodynamic function, the enthalpy H [Greek word enthalpien, to warm or heat content] as:

H = U + pV………(2)

So, equation (1) becomes

qp = H₂- H₁ = ΔH

Despite the fact that q is a path dependent function, H is a state function because it is reliant on state functions U, p, and V. As a result, H is path-independent. As a result, qp is path-independent.

Equation (2) can be written as for finite changes at constant pressure.

ΔH= ΔU + ΔpV

Since, P is constant, we can write:

ΔH = ΔU + PΔV……………(3)

It's worth noting that we're actually measuring changes in the enthalpy when heat is absorbed by the system at constant pressure. Remember  ΔH= qp , heat absorbed by the system at constant pressure. H is negative for exothermic reactions, which produce heat, and positive for endothermic reactions, which absorb heat from the environment.

As a result, equation (3) becomes U = qv at constant volume (V=0).

ΔH= ΔU=qv

Let's have a look at a gaseous reaction. If VA is the total volume of gaseous reactants, VB is the total volume of gaseous products, nA is the number of moles of gaseous reactants, and nB is the number of moles of gaseous products, then we write using the ideal gas law.,

PVA = nART

PVB = nBRT

Thus, PVB- PVA = nBRT - nART = (nB-nA)RT

Or, P(VB- VA) = (nB - nA)RT

Or, pΔV = ΔngRT……….(4)

The number of moles of gaseous products minus the number of moles of gaseous reactants is denoted by ng.

Equation (3) is obtained by substituting the value of PV from equation (4) in equation (3).

ΔH = ΔU + ΔngRT…………(5)

59. Extensive properties depend on the quantity of matter but intensive properties do not. Explain whether the following properties are extensive or intensive. Mass, internal energy, pressure, heat capacity, molar heat capacity, density, mole fraction, specific heat, temperature and molarity.

Ans: A contrast is drawn in thermodynamics between extensive and intense qualities. An extensive property is one whose value is proportional to the amount or size of matter in the system. Extensive properties include mass, volume, internal energy, enthalpy, and heat capacity, to name a few.

Properties that are independent of the amount or size of matter present are known.

As though they were intensive properties Temperature, density, and pressure, for example, are intense properties. A molar property, 𝝌m, is the value of an extensive property of the system for 1 mol of the substance. If n is the amount of matter, 𝝌m = 𝝌/n, is independent of the amount of matter. An intensive property is always the ratio of two extensive properties.

Extensive/Extensive = Intensive

E.g., Mole Fraction = Moles / Total number of moles = Extensive/Extensive

60. The lattice enthalpy of an ionic compound is the enthalpy when one mole of an ionic compound present in its gaseous state, dissociates into its ions. It is impossible to determine directly by experiment. Suggest and explain an indirect method to measure lattice enthalpy of NaCl(s).

Ans:  The enthalpy change that occurs when one mole of an ionic compound dissociates into its ions in a gaseous state is called the lattice enthalpy of an ionic compound.

Na+ + Cl- (s) → Na+ (g) + Cl- (g)

Δlattice H0 → +788 KJmol-1

Let us now calculate the lattice enthalpy of Na+Cl- (s) by following steps given below:

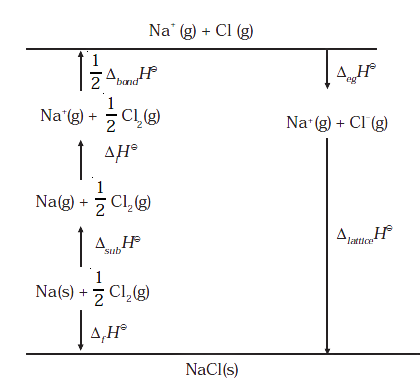
1. Na (s) → Na (g), sublimation of sodium metal, ΔsubH0 = 108.4 KJmol-1

2. Na (g) → Na+ (g) + e- (g) the ionization sodium atoms, ionization enthalpy.

ΔiH0 = 496 KJ/mol 

3. ½ Cl2 (g)  → 2Cl (g), the dissociation of chlorine, the reaction enthalpy is half the bond dissociation enthalpy.

1/2 Δbond H0 = 121 KJ/mol

4. Cl (g) + e- → Cl- (g) electron gained by chlorine atoms. The electron gain enthalpy,  

Δe.g H0 = -348.6 KJ/mol.

5. Na+(g) + Cl- (g) → Na+Cl- (s) 

61. ΔG is net energy available to do useful work and is thus a measure of “free energy”. Show mathematically that ΔG is a measure of free energy. Find the unit of ΔG. If a reaction has positive enthalpy change and positive entropy change, under what condition will the reaction be spontaneous?

Ans: We know,

ΔStotal = ΔSsys + ΔSsurr

When a system is in thermal equilibrium with its surroundings, the surroundings' temperature is the same as the system's. Furthermore, a rise in the enthalpy of the surroundings equals a decrease in the system's enthalpy. As a result of the entropy shift in the environment,

ΔSsurr = ΔHsurr/T = -ΔHsys/T

ΔStotal = ΔSsys = (-ΔHsys/T)

Rearranging the above equation:

ΔStotal = TΔSsys - ΔHsys

For spontaneous process,

ΔStotal > 0, so 

TΔSsys - ΔHsys> 0

⇒ ( - ΔHsys - TΔSsys) > 0

The above equation can be written as

- ΔG > 0

ΔG = ΔH - TΔS < 0

ΔHsys is the enthalpy change of a reaction, TΔSsys is the energy which is not available to do

useful work. As a result, G is a measure of 'free energy,' as it is the net energy available to conduct beneficial work. As a result, it's also known as the reaction's free energy. At constant pressure and temperature, G gives a set of conditions for spontaneity,

(i) If ΔG is negative (<0), the process is spontaneous.

(ii) If ΔG is positive (>0), the process is nonspontaneous.

• Unit of ΔG is Joule.

• The reaction will be spontaneous at high temperature.

62.Graphically show the total work done in an expansion when the state of an ideal gas is changed reversibly and isothermally from (Pi, Vi) to (Pf, Vf) . With the help of a pV plot compare the work done in the above case with that carried out against a constant external pressure Pf.

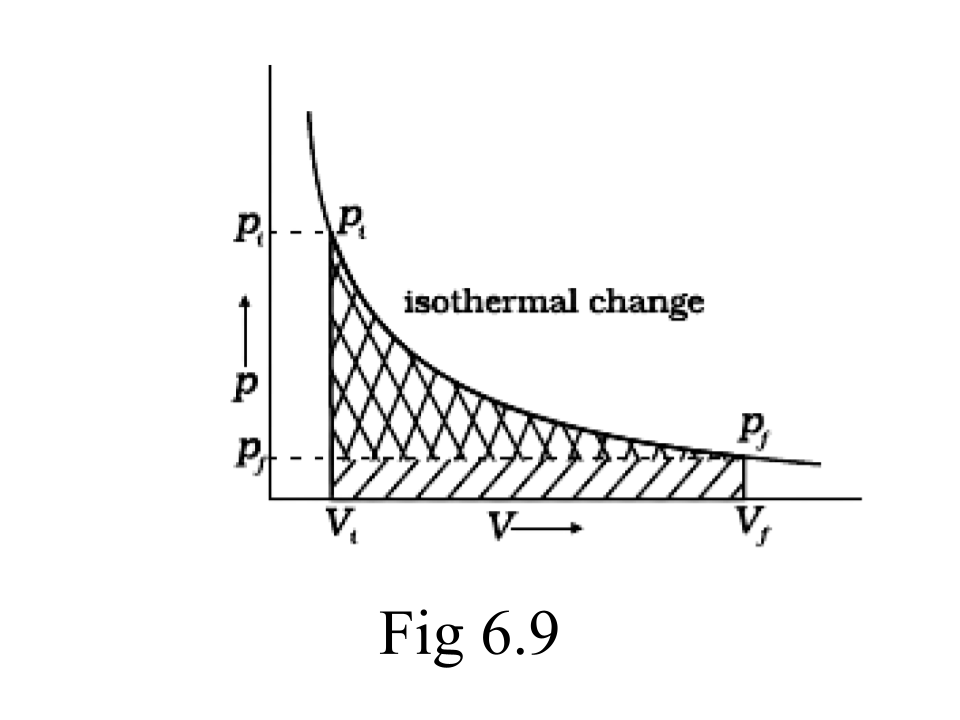
Ans: (i) Reversible work is represented by the combined areas

(ii) Work against constant pressure, Pf  is represented by the area

The Approach While Dealing With the Concept of Thermodynamics

• Since the concept of Thermodynamics and the terminologies of Chemistry are a bit new to the students, they should first learn the names of different chemical components and how to write the chemical equations properly by joining the free Classes on Vedantu and by consulting the NCERT Exemplars and Solutions books.

• While writing the chemical equations, they might make some mistakes. To avoid making errors, they should practice writing the equations at home.

• Solving previous years' question papers will help them to manage time and quickly analyze the answers in their minds.

• Comparing their own answers with the solutions provided in the NCERT Exemplar Solutions will help them to be sure of the fact that how efficient they are at answering the questions of Chemistry. It will help them to boost their confidence as well.

• Revising is extremely important when it comes to answering Chemistry questions since a lack of practice and habits of writing can make the students forget some important information that they should include in their answers. The mock papers are beneficial for them to serve this purpose

• Rational thinking plays an important part in answering the questions in Chemistry. The students need to have a clear idea of the basic physical characteristics of different chemical compounds and how they will react depending on the presence of other external factors. Practicing is the only way to sharpen their thinking ability and analysis power.