NCERT Exemplar for Class 10 Maths - Coordinate Geometry - Free PDF Download
NCERT(National Council of Educational Research and Training) has published various editions to provide a standard text for the students preparing for the Class 10th board exam. Each year an attempt is made to put the latest revision with additional material which makes the book more comprehensive. In this regard, NCERT Exemplar for Class 10 Maths is one of the most reliable available with current exam-oriented questions which have been designed and created books with utmost care. A unique feature of this book is that it is filled with various practice problems to enhance the working of the readers and at the same time develop their skills for the exam. Moreover, it offers the latest questions to make the task more difficult and interesting.
Access NCERT Exemplar Solutions for CBSE Class10 Mathematics Chapter 7 – COORDINATE GEOMETRY (Examples, Easy Methods and Step by Step Solutions)
EXERCISE 7.1
1. The distance of point $P(2,3)$ from the $x - axis $ is
(A) $2$
(B) $3$
(C) $1$
(D) $5$
Correct Answer: B.
Ans: The perpendicular distance of the point $P(2,3)$ from the $x - {\text{axis}}$ will be equal to the $y$ coordinate. So, the distance of the point $P(2,3)$ from the $x - {\text{axis}}$ is $3$ units.
Hence, the distance of the point $P(2,3)$ from the $x - {\text{axis}}$ is $3$ units.
2. The distance between the points $A(0,6)$ and $B(0, - 2)$ is
(A) $6$
(B) $8$
(C) $4$
(D) $2$
Correct answer: B.
Ans: $A({x_1},{y_1})$ and $B({x_2},{y_2})$ are two points respectively, the distance between them is given as:
$AB = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}}$
Given points are $A(0,6)$ and $B(0, - 2)$.
$AB = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}}$
$AB = \sqrt {{{(0 - 0)}^2} + {{( - 2 - 6)}^2}}$
$AB = 8$
Hence, the distance between the points $A(0,6)$ and $B(0, - 2)$ is $8.$
3. The distance of point $P(- 6,8)$ from the origin is
(A) $8$
(B) $2\sqrt 7$
(C) $10$
(D) $6$
Correct answer: C.
Ans: The distance between any two points $A({x_1},{y_1})$ and $B({x_2},{y_2})$ is given by $AB = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}}$.
Given points are $O(0,0)$ and $P( - 6,8)$.
$OP = \sqrt {{{( - 6 - 0)}^2} + {{(8 - 0)}^2}}$
$OP = \sqrt {100}$
$OP = 10$
Therefore, the distance of $P( - 6,8)$ from origin is $10$.
4. The distance between the points $(0,5)$ and $( - 5,0)$ is
(A) $5$
(B) $5\sqrt 2$
(C) $2\sqrt 5$
(D) $10$
Correct answer: B.
Ans: Distance between two points $A({x_1},{y_1})$ and $B({x_2},{y_2})$ are as follows:
$AB = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}}$
Given points are $(0,5)$ and $( - 5,0)$.
$AB = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}}$
$AB = \sqrt {{{( - 5 - 0)}^2} + {{(0 - 5)}^2}}$
$AB = \sqrt {50}$
$AB = 5\sqrt 2$
Hence, the distance between $(0,5)$ and $( - 5,0)$ is $5\sqrt 2$.
5. $AOBC$ is a rectangle whose three vertices are vertices $ A(0,3), O(0,0)$ and $B(5,0).$ The length of its diagonal is
(A) $5$
(B) $3$
(C) $\sqrt {34}$
(D) $4$
Correct answer: C.
Ans: The length of the diagonal of $AOBC$ is $AB.$
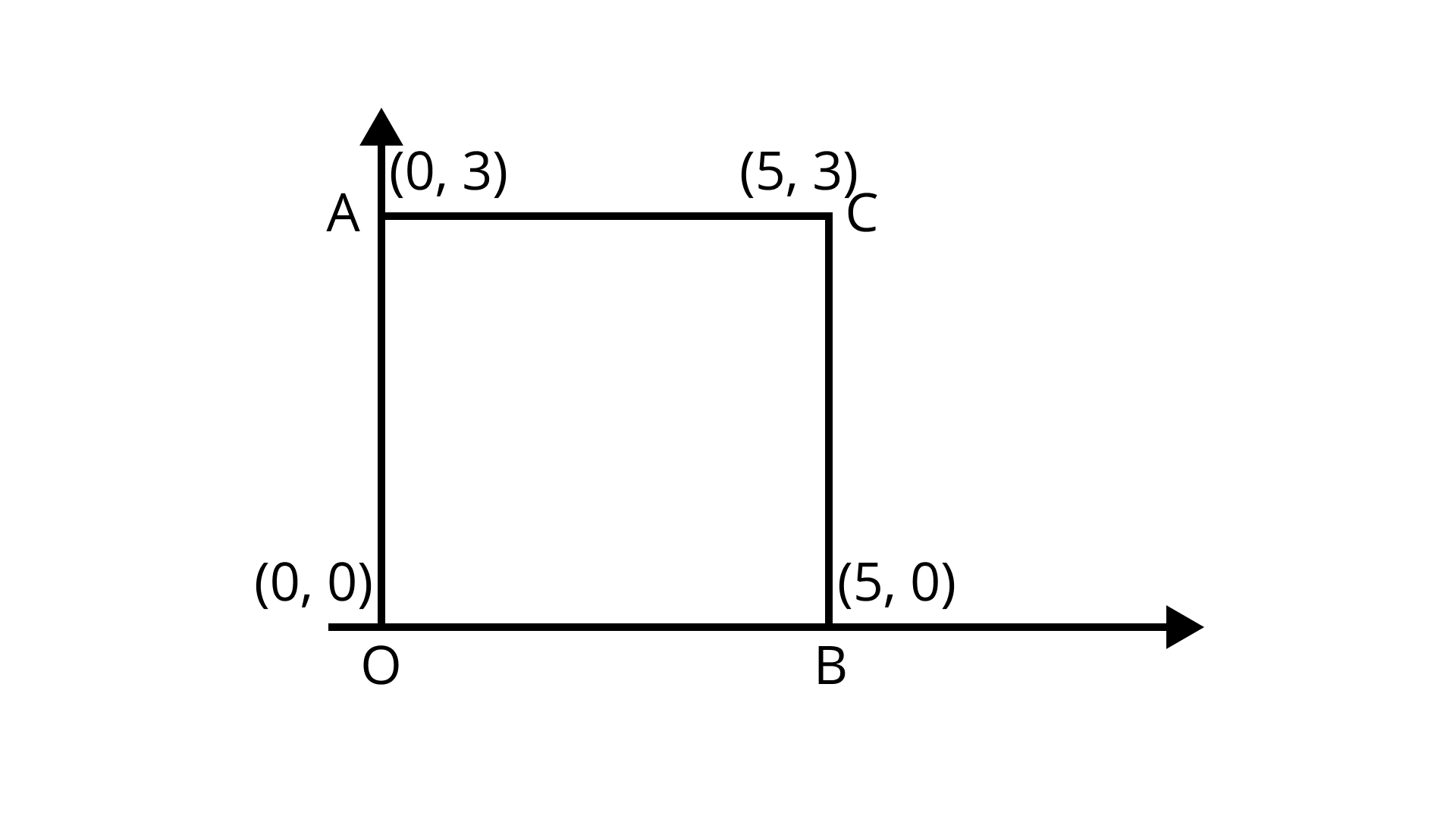
The distance between any two points $A({x_1},{y_1})$ and $B({x_2},{y_2})$ is given by $AB = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}}$
Given points are $ A(0,3), O(0,0)$ and $B(5,0).$
$AB = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}}$
$AB = \sqrt {{{(5 - 0)}^2} + {{(0 - 3)}^2}}$
$AB = \sqrt {34}$
Hence, the length of its diagonal is $\sqrt {34}$.
Question 6: The perimeter of a triangle with vertices $ (0,4), (0,0)$ and $(3,0)$ is
(A) $5$
(B) $12$
(C) $11$
(D) $7 + \sqrt 5$
Correct answer: B.
Ans: Perimeter of triangle $\Delta ABC = AB + BC + AC$.
$(0,4), (0,0)$ and $C(3,0)$ are the three vertices of $\Delta ABC.$
Two points $A({x_1},{y_1})$ and $B({x_2},{y_2})$ are at distance as below
$AB = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}}$
$\Rightarrow AB = \sqrt {{{(0 - 0)}^2} + {{(0 - 4)}^2}}$
$\Rightarrow AB = 4$
$\Rightarrow AC = \sqrt {{{(3 - 0)}^2} + {{(0 - 4)}^2}}$
$\Rightarrow AC = 5$
$\Rightarrow BC = \sqrt {{{(3 - 0)}^2} + {{(0 - 0)}^2}}$
$\Rightarrow BC = 3$
Perimeter of $\Delta ABC = 4 + 5 + 3$
Perimeter of $\Delta ABC = 12 cm$
Hence, the perimeter of a triangle with vertices $ (0,4), (0,0)$ and $(3,0)$ is $12cm$.
7. The area of a triangle with vertices $A(3,0), B(7,0)$ and $C(8,4)$ is
(A) $14$
(B) $28$
(C) $8$
(D) $6$
Correct answer: C.
Ans: $ A(3,0), B(7,0)$ and $C(8,4)$ are the three vertices of $\Delta ABC.$
Area of triangle $\Delta ABC = \dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right]$
Area of triangle $\Delta ABC = \dfrac{1}{2}\left[ {3\left( {0 - 4} \right) + 7\left( {4 - 0} \right) + 8\left( {0 - 0} \right)} \right]$
$\Delta ABC = 8 sq.units$
Hence, the area of a triangle with vertices $A(3,0), B(7,0)$ and $C(8,4)$ is $8 sq.units$.
8. The points $(- 4,0), (4,0), (0,3)$ are the vertices of a
(A) Right triangle
(B) Isosceles triangle
(C) Equilateral triangle
(D) Scalene triangle
Correct answer: B.
Ans: Two points $A({x_1},{y_1})$ and $B({x_2},{y_2})$ are at a distance, which is derived as follows:
$AB = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}}$
$\Rightarrow AB = \sqrt {{{(4 + 4)}^2} + {{(0 - 0)}^2}}$
$\Rightarrow AB = 8$
$\Rightarrow AC = \sqrt {{{(0 + 4)}^2} + {{(3 - 0)}^2}}$
$\Rightarrow AC = 5$
$\Rightarrow BC = \sqrt {{{(0 - 4)}^2} + {{(3 - 0)}^2}}$
$\Rightarrow BC = 5$
$AC = BC = 5 cm\: and\: AB = 8 cm{\text{.}}$
Hence, the points $ ( - 4,0), (4,0), (0,3)$ are the vertices of an isosceles triangle.
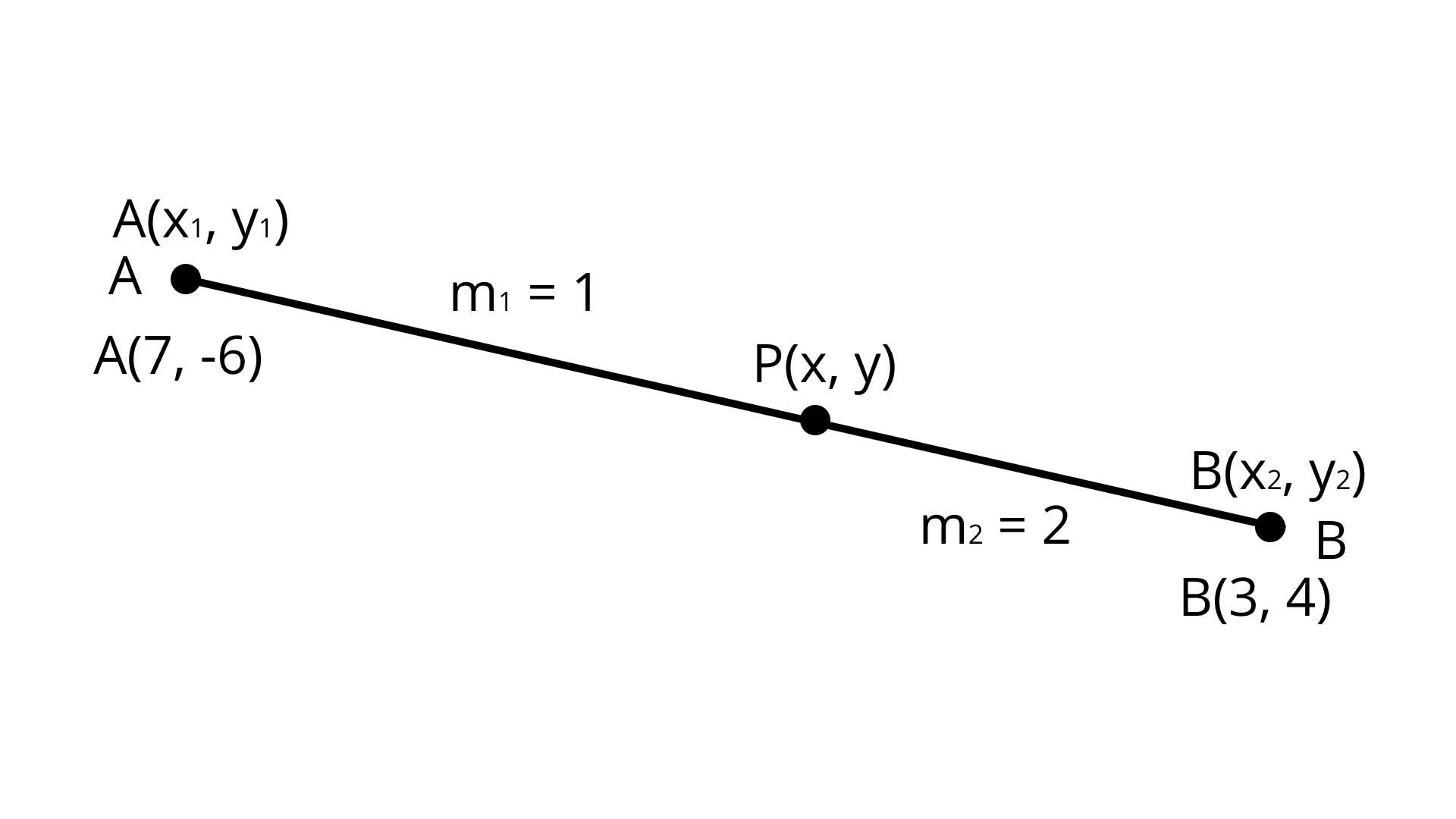
9. The point which divides the line segment joining the points $(7, - 6)$ and $(3,4)$ in ratio $1:2$ internally lies in the
(A) I quadrant
(B) II quadrant
(C) III quadrant
(D) IV quadrant
Correct answer: D.
Ans: As $x = \dfrac{{{m_1}{x_2} + {m_2}{x_1}}}{{{m_1} + {m_2}}}$ and $y = \dfrac{{{m_1}{y_2} + {m_2}{y_1}}}{{{m_1} + {m_2}}}$
Here, ${m_1} = 1, {m_2} = 2$.
$\Rightarrow (x,y) = \left( {\dfrac{{1(3) + 2(7)}}{{1 + 2}},\dfrac{{1(4) + 2( - 6)}}{{1 + 2}}} \right)$
$\Rightarrow (x,y) = \left( {\dfrac{{17}}{3},\dfrac{{ - 8}}{3}} \right)$
Hence, we can conclude by saying that the line segment is divided by the line joining $(7, - 6)$ and $(3,4)$ in ratio $1:2$ internally lies in IV quadrant.
10. The point which lies on the perpendicular bisector of the line segment joining the points $A( -2, -5)$ and $B(2,5)$ is
(A) $(0, 0)$
(B) $(0, 2)$
(C) $(2, 0)$
(D) $( - 2, 0)$
Correct answer: A.
Ans: Through the midpoint of $AB$, the perpendicular bisector of AB passes.
The midpoint of the line joining $A({x_1},{y_1})$ and $B({x_2},{y_2})$ is given by $\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$.
Mid-point $= \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$
Mid-point $= \left( {\dfrac{{ - 2 + 2}}{2},\dfrac{{ - 5 + 5}}{2}} \right)$
Mid-point $= \left( {0, 0} \right)$
Hence, the point lying on the perpendicular bisector of the line segment joining the points $A(- 2, - 5)$ and $B(2, 5)$ is $\left( {0, 0} \right)$.
11. The fourth vertex $D$ of a parallelogram $ABCD$ whose three vertices are $A( - 2, 3), B(6, 7)$ and $C(8, 3)$ is
(A) $(0, 1)$
(B) $(0, - 1)$
(C) $( - 1, 0)$
(D) $(1, 0)$
Correct answer: B.
Ans:
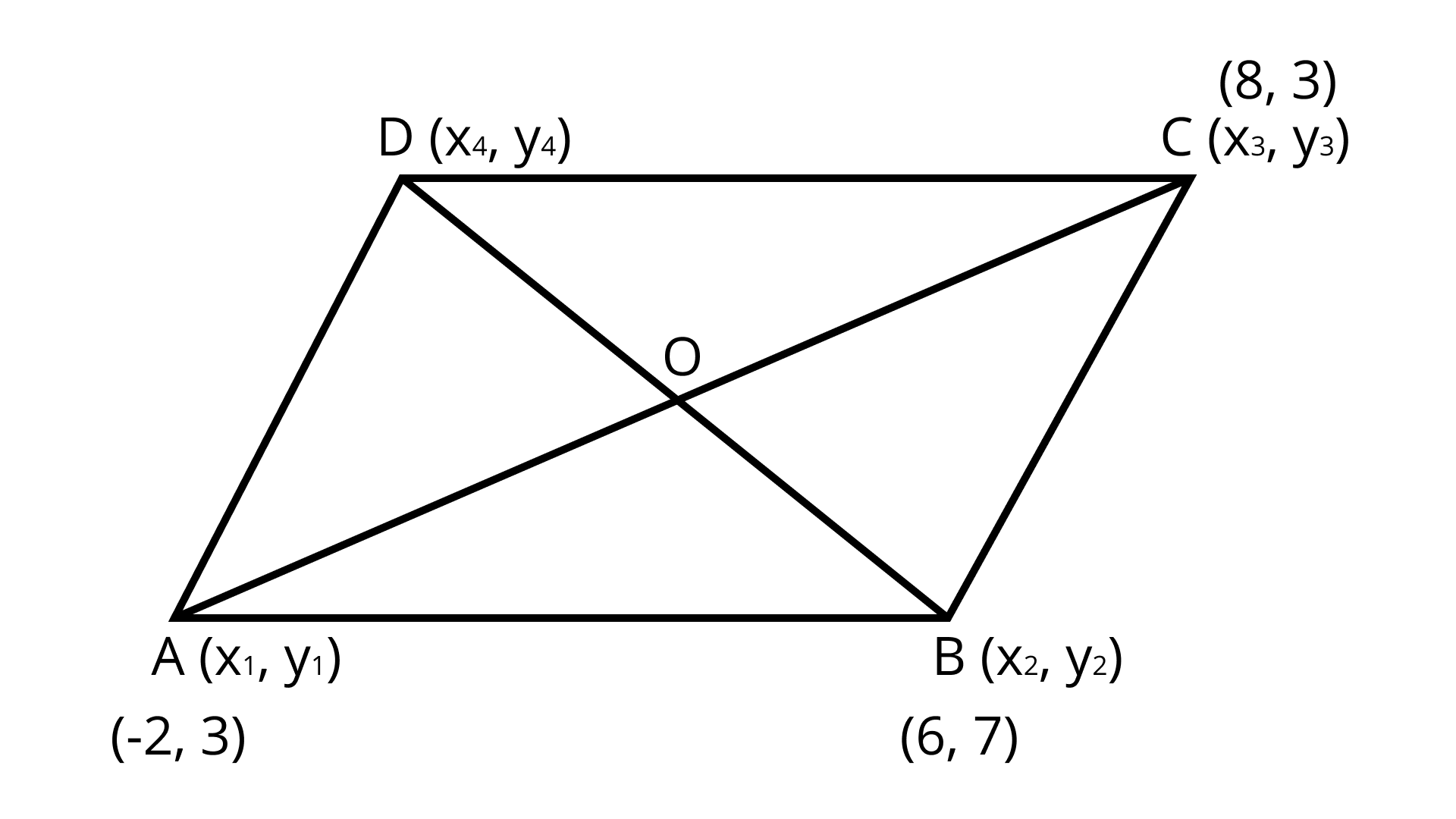
Note that the diagonals $AC$ and $BD$ of parallelogram $ABCD$ bisect each other. So, the midpoint of $AC$ is equal to the midpoint of $BD$.
The midpoint of $A({x_1},{y_1})$ and $B({x_2},{y_2})$ is given by $\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$.
$\Rightarrow \left( {\dfrac{{ - 2 + 8}}{2},\dfrac{{3 + 3}}{2}} \right) = \left( {\dfrac{{{x_4} + 6}}{2},\dfrac{{{y_4} + 7}}{2}} \right)$
$\Rightarrow \left( {3,3} \right) = \left( {\dfrac{{{x_4} + 6}}{2},\dfrac{{{y_4} + 7}}{2}} \right)$
Now, compare both sides:
$\dfrac{{{x_4} + 6}}{2} = 3$ and $\dfrac{{{y_4} + 7}}{2} = 3$
${x_4} = 0$ and ${y_4} = - 1$
$({x_4},{y_4}) = (0, - 1)$
Hence, the fourth vertex $D$ of a parallelogram $ABCD$ is $(0, - 1)$.
12. If the point $P(2, 1)$ lies on the line segment joining points $A(4, 2)$ and $B(8, 4)$ then
(A) $AP = \dfrac{1}{3}AB$
(B) $AP = PB$
(C) $PB = \dfrac{1}{3}AB$
(D) $AP = \dfrac{1}{2}AB$
Correct answer: D.
Ans:
Let ${m_1} = k,{m_2} = 1$.
As $x = \dfrac{{{m_1}{x_2} + {m_2}{x_1}}}{{{m_1} + {m_2}}}$ and $y = \dfrac{{{m_1}{y_2} + {m_2}{y_1}}}{{{m_1} + {m_2}}}$ ,
$\Rightarrow 2 = \dfrac{{k(8) + 1(4)}}{{k + 1}}$ and $1 = \dfrac{{k(4) + 1(2)}}{{k + 1}}$
$\Rightarrow 8k + 4 = 2k + 2$ and $4k + 2 = k + 1$
$\Rightarrow k = \dfrac{{ - 1}}{3}$ and $k = \dfrac{{ - 1}}{3}$
So, $\dfrac{{AP}}{{PB}} = \dfrac{{ - 1}}{3}$
$\Rightarrow AP = - 1$, which means $1$ part outside $AB.$
And $PB = 3$
$\Rightarrow AP = 1x$ unit and $AB = 3x - 1x = 2x$ units.
So, $AP = \dfrac{1}{2}AB$.
Hence, $AP = \dfrac{1}{2}AB$.
13. If $P\left( {\dfrac{a}{3},4} \right)$ is the midpoint of the line segment joining the points $Q(- 6, 5)$ and $R(- 2, 3)$ then the value of $a$ is
(A) $- 4$
(B) $- 12$
(C) $12$
(D) $- 6$
Correct answer: B.
Ans: $P({x_1},{y_1})$ and $Q({x_2},{y_2})$ equation’s midpoint is given by $\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$.
$\Rightarrow \left( {\dfrac{a}{3},4} \right) = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$
$\Rightarrow \left( {\dfrac{a}{3},4} \right) = \left( {\dfrac{{ - 6 - 2}}{2},\dfrac{{5 + 3}}{2}} \right)$
$\Rightarrow \dfrac{a}{3} = \dfrac{{ - 8}}{2}$
$\Rightarrow a = - 12$
Hence, $a = - 12$.
14. The perpendicular bisector of the line segment joining the points $A(1, 5)$ and $B(4, 6)$ cuts the y-axis at
(A) $(0, 13)$
(B) $(0, - 13)$
(C) $(0, 12)$
(D) $(13, 0)$
Correct answer: A.
Ans: The point where the perpendicular bisector of the line segment joining $A(1, 5)$ and $B(4, 6)$ cuts the y-axis $P(0, y).$
$AP = BP$
$\Rightarrow A{P^2} = B{P^2}$
$\Rightarrow 1 + {(y - 5)^2} = 16 + {(y - 6)^2}$
$\Rightarrow 1 + {y^2} - 10y + 25 = 16 + {y^2} - 12y + 36$
$\Rightarrow y = 13$
So, the point $P(0, y) = (0, 13)$.
15. The coordinates of the point which is equidistant from the three vertices of the $\Delta AOB$ as shown in the Fig. 7.1 is
(A) $(x,y)$
(B) $(y,x)$
(C) $\left( {\dfrac{x}{2},\dfrac{y}{2}} \right)$
(D) $\left( {\dfrac{y}{2},\dfrac{x}{2}} \right)$
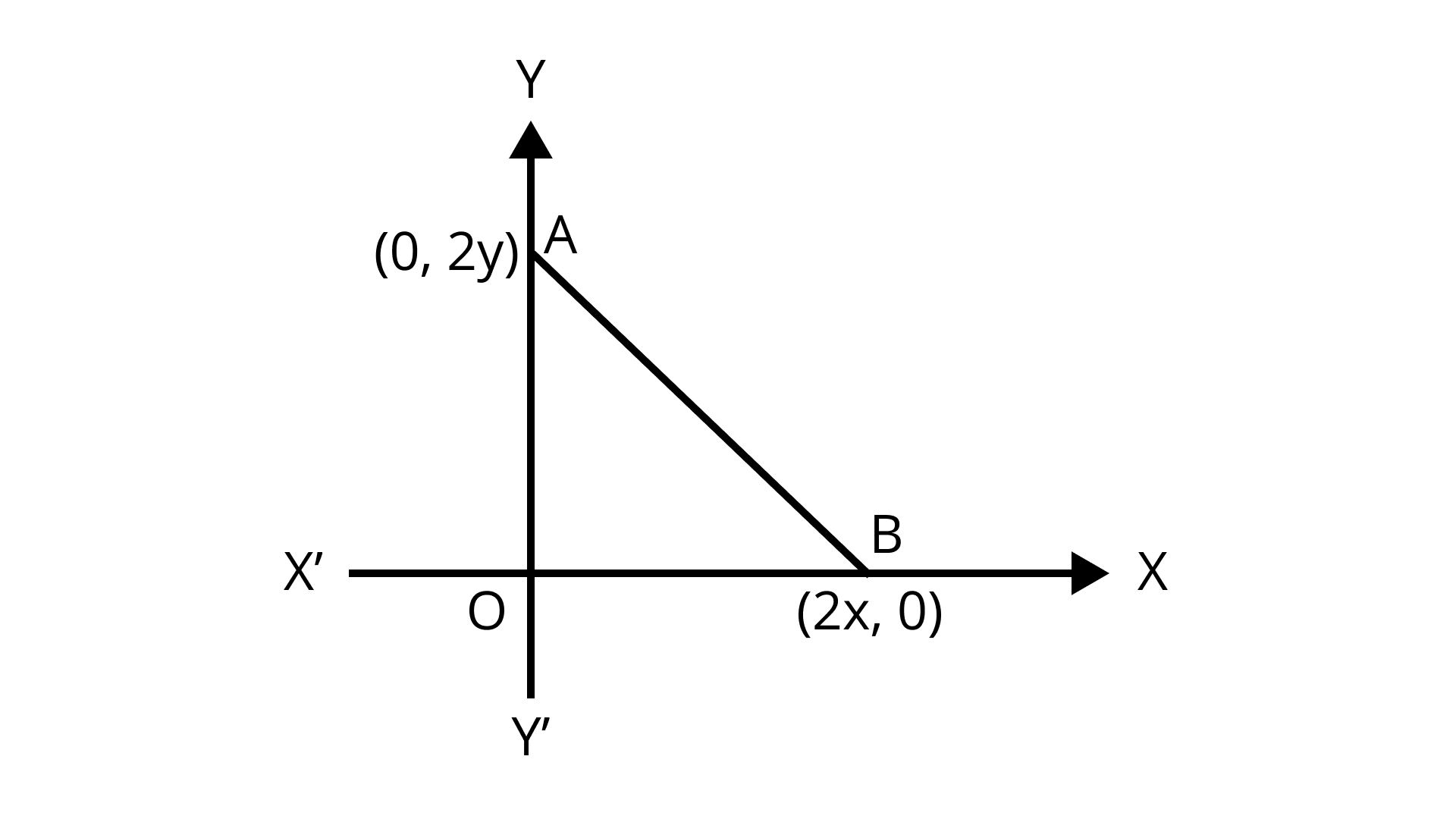
Correct answer: A.
Ans: In any right-angled triangle, the mid-point of the hypotenuse will be equidistant from all the three vertices of the triangle.
The midpoint of $A({x_1},{y_1})$ and $B({x_2},{y_2})$ is given by $\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$.
Midpoint of $A(0,2y)$ and $B(2x,0)$ is $\left( {\dfrac{{2x + 0}}{2},\dfrac{{0 + 2y}}{2}} \right) = (x, y)$.
Hence, the coordinates of the point which is equidistant from the three vertices of the $\Delta AOB$ is $(x, y)$.
16. A circle drawn with origin as the center passes through $\left( {\dfrac{{13}}{2},0} \right).$ The point which does not lie in the interior of the circle is
(A) $\left( {\dfrac{{ - 3}}{4},1} \right)$
(B) $\left( {2,\dfrac{7}{3}} \right)$
(C) $\left( {5,\dfrac{{ - 1}}{2}} \right)$
(D) $\left( { - 6,\dfrac{5}{2}} \right)$
Correct answer: D.
Ans: The distance between any two points $A({x_1},{y_1})$ and $B({x_2},{y_2})$ is given by $AB = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}}$ .
The radius of the circle is $\sqrt {{{\left( {\dfrac{{13}}{2} - 0} \right)}^2} + {{(0 - 0)}^2}} = 6.5$ units.
Consider the point given in option A,
The distance of $\left( {\dfrac{{ - 3}}{4},1} \right)$ from origin is $\sqrt {{{\left( {\dfrac{{ - 3}}{4} - 0} \right)}^2} + {{(1 - 0)}^2}} = 1.25$ units.
As the distance $1.25 < 6.5$, the point $\left( {\dfrac{{ - 3}}{4},1} \right)$ lies in the interior of the given circle.
Consider the point given in option B.
The distance of $\left( {2,\dfrac{7}{3}} \right)$from origin is $\sqrt {{{\left( {2 - 0} \right)}^2} + {{\left( {\dfrac{7}{3} - 0} \right)}^2}} = 3.0731$ units.
As the distance $3.0731 < 6.5$, the point $\left( {2,\dfrac{7}{3}} \right)$ lies in the interior of the given circle.
Consider the point given in option C,
The distance of $\left( {5,\dfrac{{ - 1}}{2}} \right)$ from origin is $\sqrt {{{(5 - 0)}^2} + {{\left( { - \dfrac{1}{2} - 0} \right)}^2}} = 5.0249$units.
As the distance $5.0249 < 6.5$ , the point $\left( {5,\dfrac{{ - 1}}{2}} \right)$ lies in the interior of the given circle.
Consider the point given in option D,
The distance of $\left( { - 6,\dfrac{5}{2}} \right)$ from origin is $\sqrt {{{( - 6 - 0)}^2} + {{\left( {\dfrac{5}{2} - 0} \right)}^2}} = 6.5$ units.
As the distance $6.5 = 6.5$, the point $\left( { - 6,\dfrac{5}{2}} \right)$ lies on the given circle.
Hence, the point which does not lie in the interior of the circle is $\left( { - 6,\dfrac{5}{2}} \right)$.
17. A line intersects the y-axis and x-axis at the points $P$ and $Q$ respectively. If $(2, - 5)$ is the midpoint of $PQ$ then the coordinates of $P$ and $Q$ are, respectively
(A) $(0, - 5)$ and $(2,0)$
(B) $(0,10)$ and $( - 4,0)$
(C) $(0,4)$ and $( - 10,0)$
(D) $(0, - 10)$ and $(4,0)$
Correct answer: D.
Ans: As $P$ lies on y-axis, the coordinates of $P$ will be $(0, y).$
As $Q$ lies on x-axis, the coordinates of $Q$ will be $(x, 0).$
The midpoint of $P({x_1},{y_1})$ and $Q({x_2},{y_2})$ is given by $\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$.
$\Rightarrow \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right) = (2, - 5)$
$\Rightarrow \left( {\dfrac{{0 + x}}{2},\dfrac{{y + 0}}{2}} \right) = (2, - 5)$
$\Rightarrow x = 4 and y = - 10$
Hence, the coordinates of $P$ and $Q$ are $(0, - 10)$ and $(4,0)$.
18. The area of a triangle with vertices (a,b + c), (b,c + a) and (c,a + b) is
(A) ${(a + b + c)^2}$
(B) 0
(C) a + b + c
(D) abc
Correct Answer: B
Ans: That area of triangle $\Delta ABC = \dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right]$.
Vertices are (a,b + c), (b,c + a) and (c,a + b).
Area = $\dfrac{1}{2}\left[ {a\{ c + a - \left( {a + b} \right)\} + b\{ a + b - (b + c)\} + c\{ b + c - (c + a)\} } \right]$
Area = $\dfrac{1}{2}\left[ {a\left( {c - b} \right) + b(a - c) + c(b - a)} \right]$
Area = $\dfrac{1}{2}\left[ {ac - ab + ab - bc + bc - ac} \right]$
Area = 0
Hence, Area of triangle = 0.
19. If the distance between the points $(4,p)$ and $(1,0)$ is $5$ then the value of $p$ is
(A) $4$ only
(B) $ \pm 4$
(C) $ - 4$ only
(D) $0$
Correct answer: B.
Ans: The distance between any two points $A({x_1},{y_1})$ and $B({x_2},{y_2})$ is given by $AB = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}}$ .
Given $AB = 5$units
$\Rightarrow {\left( {AB} \right)^2} = {\left( 5 \right)^2}$
$\Rightarrow {(4 - 1)^2} + {(p - 0)^2} = 25$
$\Rightarrow 9 + {(p)^2} = 25$
$\Rightarrow {(p)^2} = 16$
$\Rightarrow p = \pm 4$
Hence, $p = \pm 4.$
20. If the points $A(1,2), O(0,0)$ and $C(a,b)$ are collinear, then
(A) $a = b$
(B) $a = 2b$
(C) $2a = b$
(D) $a = - b$
Correct answer: C.
Ans: Area of triangle $\Delta ABC = \dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right]$.
Area of a triangle is zero if the points are collinear.
$\Rightarrow \dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right] = 0$
$\Rightarrow \dfrac{1}{2}\left[ {1\left( {0 - b} \right) + 0\left( {b - 2} \right) + a\left( {2 - 0} \right)} \right] = 0$
$\Rightarrow \dfrac{1}{2}( - b + 2a) = 0$
$\Rightarrow \dfrac{1}{2}( - b + 2a) = 0$
$\Rightarrow 2a = b$
Hence, $2a = b.$
EXERCISE 7.2
1. $\Delta ABC$ With vertices $A( - 2, 0), B(2, 0)$ and $C(0, 2)$ is similar to $\Delta DEF$ with vertices $D (- 4, 0),E(4,0)$ and $F$ $(0, 4)$
Ans: The statement is False.
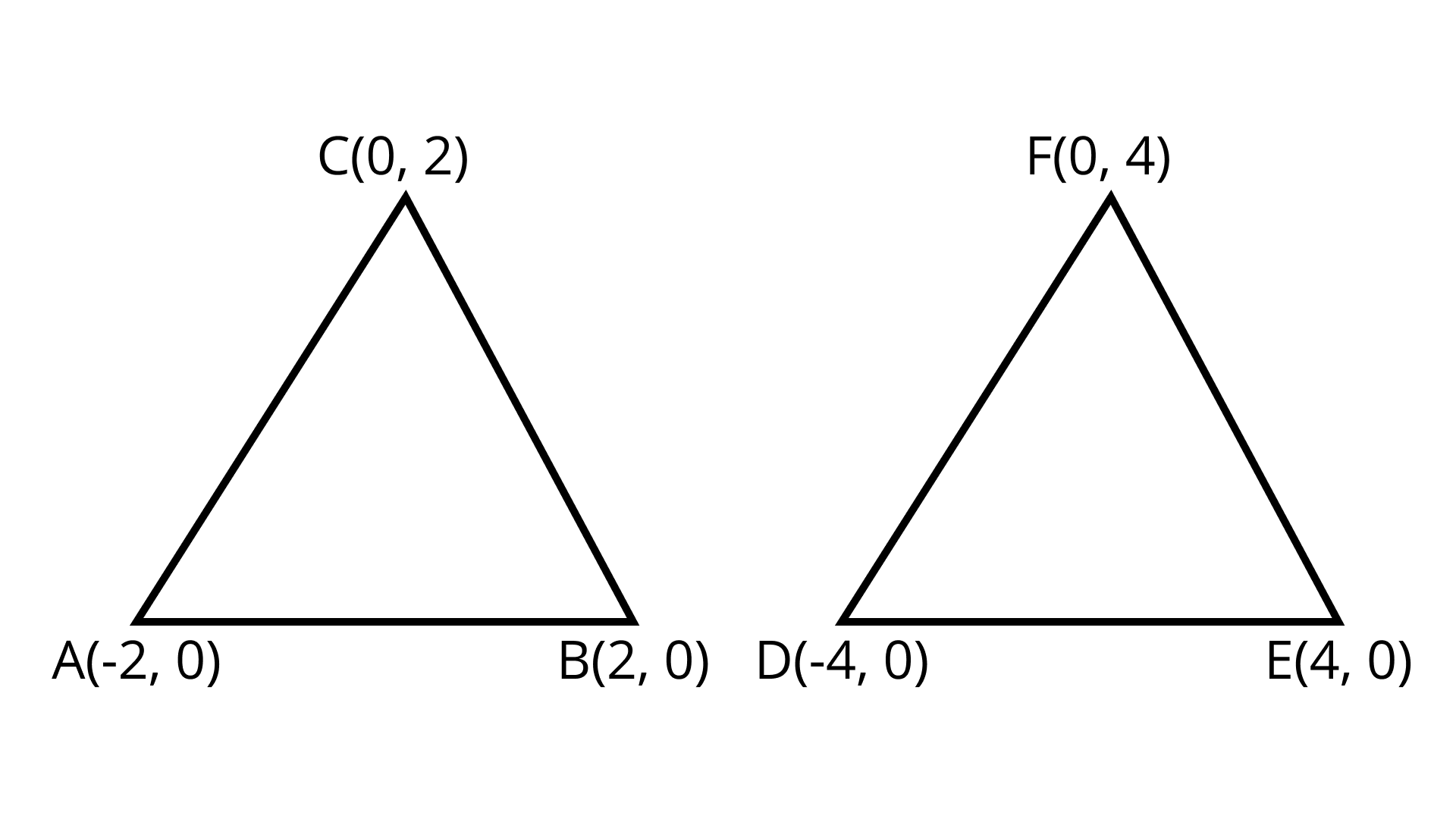
Distance Formula $= \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
In $\Delta ABC$ , $AB = \sqrt {{{(2 + 2)}^2} + {{(0 - 0)}^2}} = \sqrt {{{(4)}^2}} = 4$
$AC = \sqrt {{{(0 + 2)}^2} + {{(2 - 0)}^2}} = \sqrt {(4 + 4)} = 2\sqrt 2$
in $\Delta DEF$ , $DE = \sqrt {{{(4 + 4)}^2} + {{(0 - 0)}^2}} = \sqrt {{{(8)}^2}} = 8$
$EF = \sqrt {{{(0 - 4)}^2} + {{(4 - 0)}^2}} = \sqrt {16 + 16} = \sqrt {32} = 4\sqrt 2$
$DF = \sqrt {{{(0 + 4)}^2} + {{(4 - 0)}^2}} = \sqrt {16 + 16} = 4\sqrt 2$
Here, $\dfrac{{AB}}{{DE}} = \dfrac{{BC}}{{EF}} = \dfrac{{AC}}{{DF}}$
$\dfrac{4}{8} = \dfrac{{2\sqrt 2 }}{{4\sqrt 2 }} = \dfrac{1}{2}$
Hence, $\Delta ABC$ is similar to $\Delta DEF$.
2. Point $P( - 4,2)$ lies on the line segment joining the points $A( - 4,6)$ and $B( - 4, - 6)$
Ans: The statement is True
The given points $A( - 4, 6)$ and $B( - 4, - 6)$
$\left( {{x_1},{y_1}} \right) = ( - 4, 6)$
$\left( {{x_2},{y_2}} \right) = ( - 4, - 6)$
$\left( {{x_3},{y_3}} \right) = ( - 4, 2)$
Point $P( - 4, 2)$ lie on line AB if the area of triangle $ABP = 0$
$\dfrac{1}{2}[ - 4( - 6 - 2) - 4(2 - 6) - 4(6 + 6)]$
$\dfrac{1}{2}[ - 4( - 8) - 4( - 4) - 4(12)]$
$[32 + 16 - 48]$
$= 0$
$\therefore P( - 4, 2)$ Must lie on line joining, $AB$
3. The points $(0, 5), (0, - 9)$ and $(3, 6)$ are collinear.
Ans: The statement is False
The given points area $(0, 5),(0, - 9)$ and $(3, 6)$
If the point area is collinear then the area of triangle is 0.
${x_1} = 0, {x_2} = 0, {x_3} = 3$
${y_1} = 5, {y_2} = 9, {y_3} = 6$
$= \dfrac{1}{2} [0 ( - 9 - 6) + 0 (6 - 5) + 3 (5 + 9)]$
$= \dfrac{1}{2}[0 + 0 + 42]$
$= \dfrac{{42}}{2} = 21$
Area of triangle $= 21$
Here the area of the triangle is not equal to zero.
Hence, the point is not collinear.
4. Point $ P\left( {0, 2} \right)$ is the point of intersection of y–axis and perpendicular bisector of line segment joining the points $A ( - 1, 1)$ and $B (3, 3)$
Ans: The statement is False.
If the point ${\text{P}}$ is a perpendicular bisector of the line joining the point $A( - 1, 1)$ and $B(3, 3)$ then it must be mid-point of $AB$.
Mid - point of $AB = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$
$\left( {{x_1},{y_1}} \right) = ( - 1, 1)$
$\left( {{x_2},{y_2}} \right) = (3, 3)$
It does not represent point P
Hence, the given statement is false.
5. Points $A \left( {3, 1} \right), B \left( {12, -2} \right) and C \left( {0, 2} \right)$ cannot be the vertices of a triangle.
Ans: The statement is True
If they are not the vertices of a triangle then
Area of $\Delta ABC = 0$
${x_1} = 3, {x_2} = 12, {x_3} = 0$
${y_1} = 1, {y_2} = - 2, {y_3} = 2$
Let us find the area of $\Delta ABC$
$= \dfrac{1}{2}[3( - 2 - 2) + 12(2 - 1) + 0(1 + 2)]$
$= \dfrac{1}{2}[3( - 4) + 12(1) + 0]$
$= \dfrac{1}{2}[ - 12 + 12]$
$= \dfrac{0}{2}$
$= 0$
Area of $\Delta ABC = 0$
Hence, they are collinear or not the vertices of a triangle.
6. Points $A \left( {4, 3} \right), B \left( {6, 4} \right), C \left( {5, --6} \right) and D \left( {--3, 5} \right)$ are the vertices of a parallelogram.
Ans: The statement is False
The given points area $A(4,3),B(6,4),C(5, - 6),D( - 3,5)$
Distance between $AB = \sqrt {{{(6 - 4)}^2} + {{(4 - 3)}^2}}$
$AB = \sqrt {{{(2)}^2} + {{(1)}^2}} = \sqrt 5$
Distance between $BC = \sqrt {{{(5 - 6)}^2} + {{( - 6 - 4)}^2}}$
$BC = \sqrt {1 + 100} = \sqrt {101}$
Distance between $CD = \sqrt {{{( - 3 - 5)}^2} + {{(5 + 6)}^2}}$
$CD = \sqrt {64 + 121} = \sqrt {185}$
Distance between $DA = \sqrt {{{(4 + 3)}^2} + {{(3 - 5)}^2}}$
$DA = \sqrt {49 + 4} = \sqrt {53}$
Here, opposite sides are not equal i.e.
$AB \ne CD,BC \ne DA$
Hence, it is not a parallelogram
7. A circle has its Centre at the origin and a point $P\left( {5, 0} \right)$ lies on it. The point $Q\left( {6, 8} \right)$ lies outside the circle.
Ans: The statement is True.
The center of the circle is $O(0,0)$
If point $P(5,0)$ lies on the circle then the distance between $O(0, 0)$ and $P(5, 0)$ is the radius of the circle $OP = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
$OP = \sqrt {{{(5 - 0)}^2} + {{(0 - 0)}^2}}$
$OP = \sqrt {{{(5)}^2}} = 5$
$OP = 5$
Radius of circle $= 5$
If point $Q(6, 8)$ is outside the circle then the distance between $O (0,0)$ and $Q (6,8)$ is greater than the Radius of the circle
$\left( {{x_1},{y_1}} \right) = (0, 0)$
$\left( {{x_2},{y_2}} \right) = (6, 8)$
$OQ = \sqrt {{{(6 - 0)}^2} + {{(8 - 0)}^2}}$
$OQ = \sqrt {36 + 64}$
$= \sqrt {100} = 10$
Here point $OQ$ is greater than the radius of circle.
Hence, point $Q(6, 8)$ lies outside the circle.
8. The point $A(2, 7)$ lies on the perpendicular bisector of line segment joining the points $P(6, 5)$ and $Q(0, - 4)$
Ans: The statement is False.
If point $A(2, 7)$ is bisector then it must be mid-point of the line joining the points $P(6, 5)$ and $Q(0, - 4)$
Mid - point of $PQ = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$
$\left( {{x_1},{y_1}} \right) = (6,5)$
$\left( {{x_2},{y_2}} \right) = (0, - 4)$
$= \left( {\dfrac{{6 + 0}}{2},\dfrac{{5 - 4}}{2}} \right) = \left( {3,\dfrac{1}{2}} \right)$
Hence, A does not lies on bisector.
9. Point $C \left( {5, -3} \right)$ is one of the two points of trisection of the line segment joining the points $A \left( {7, - 2} \right)$ and B $\left( {1, - 5} \right)$
Ans: The statement is True
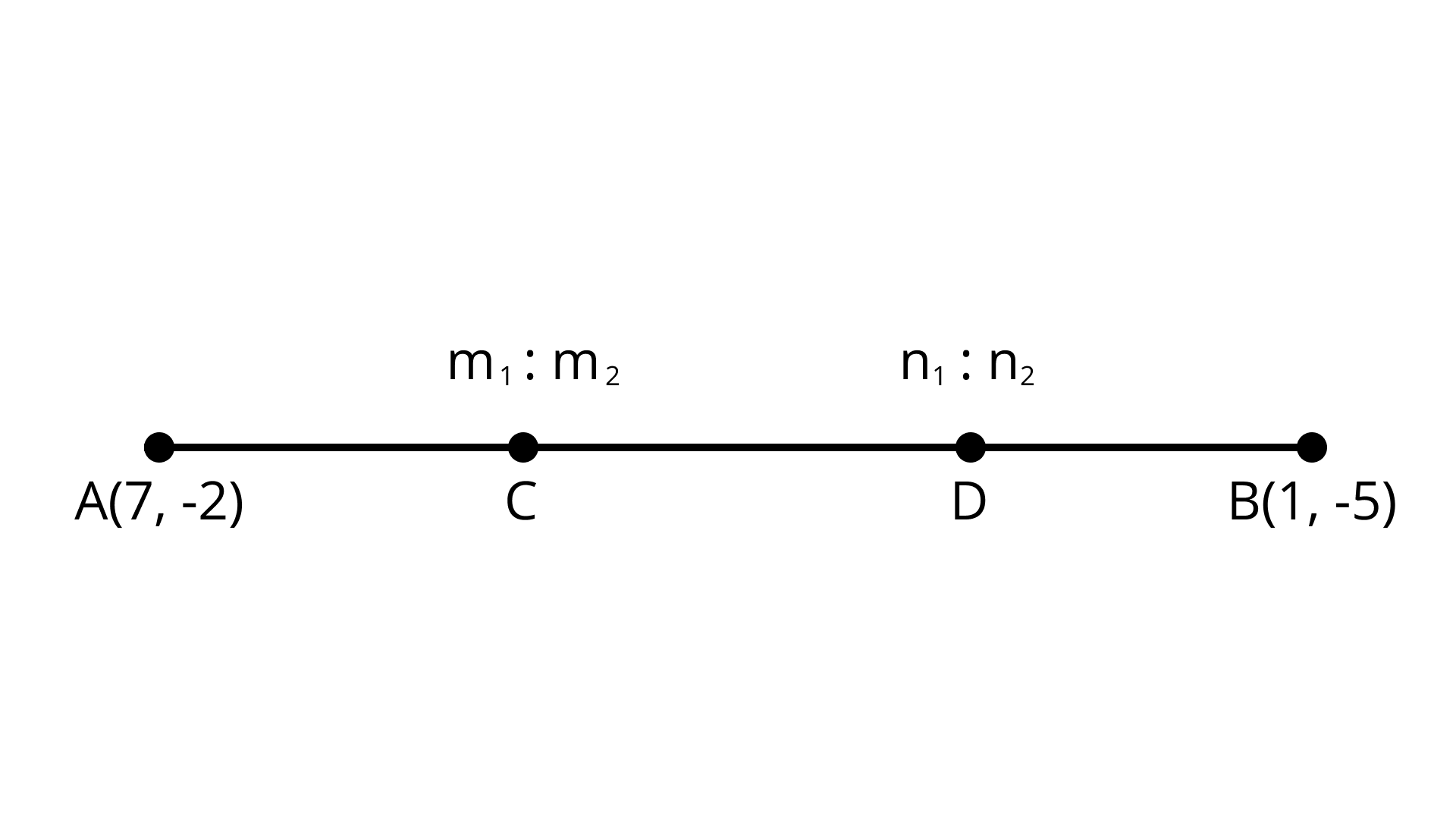
Let the two point of trisection are C, D
$\left( {{x_1},{y_1}} \right) = (7, - 2)$
$\left( {{x_2},{y_2}} \right) = (1, - 5)$
${m_1} = 1,{m_2} = 2$ $\because$ C divide in ratio 1:2
$C = \left( {\dfrac{{1 \times 1 + 2 \times 7}}{{1 + 2}},\dfrac{{1 \times \left( { - 5} \right) + 2 \times \left( { - 2} \right)}}{{1 + 2}}} \right)$
$C = \left( {\dfrac{{1 + 14}}{3},\dfrac{{ - 5 - 4}}{3}} \right)$
$C = (5, - 3)$
${n_1} = 2,{n_2} = 1$ $\because$ C divide in ratio 2:1
$D = \left( {\dfrac{{2 \times 1 + 1 \times 7}}{{2 + 1}},\dfrac{{2 \times \left( { - 5} \right) + 1 \times \left( { - 2} \right)}}{{2 + 1}}} \right)$
$D = \left( {\dfrac{{2 + 7}}{3},\dfrac{{ - 10 - 2}}{3}} \right)$
$D = (3, - 4)$
Hence, the given statement is true.
10. Points $A( - 6,10), B ( - 4,6)$ and $C (3, - 8)$ are collinear such that $AB = \dfrac{2}{9}AC$
Ans: The statement is True.
If the points $A( - 6,10), B( - 4,6)$ and $C(3, - 8)$ are collinear then area of $\Delta ABC = 0$ $= \dfrac{1}{2}[ - 84 + 72 + 12]$
Area of $\Delta ABC = 0$
Hence, ${\text{A}},{\text{B}}$ and ${\text{C}}$ are collinear
Distance between $AB = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
$AB = \sqrt {{{( - 4 + 6)}^2} + {{(6 - 10)}^2}}$
$AB = \sqrt {4 + 16} = \sqrt {20} = 2\sqrt 5$
Distance between $AC = \sqrt {{{(3 + 6)}^2} + {{( - 8 - 10)}^2}}$
$= \sqrt {81 + 324}$
$= \sqrt {405}$
$AC = 9\sqrt 5$
Hence, $\dfrac{{AB}}{{AC}} = \dfrac{{2\sqrt 5 }}{{9\sqrt 5 }}$
$AB = \dfrac{2}{9}AC$
11. The point $P( - 2, 4)$ lies on a circle of radius $6$ and Centre $C(3, 5)$
Ans: The statement is False
The radius of the circle is $6$ and Centre $C (3, 5)$
If point $P (- 2,4)$ lies on the circle then the distance between the Centre and point $P$ is equal to the radius of the circle.
Distance between $PC = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
$\left( {{x_1},{y_1}} \right) = ( - 2,4)$
$\left( {{x_2},{y_2}} \right) = (3,5)$
$PC = \sqrt {{{(3 + 2)}^2} + {{(5 - 4)}^2}}$
$PC = \sqrt {25 + 1} = \sqrt {26}$
$PC \ne radius (6)$
Hence, point $P ( - 2, 4)$ not lies on the circle with Centre$C (3, 5)$.
12. The points A(- 1, - 2),B(4, 3),C(2, 5)$ and D( - 3, 0) in that order form a rectangle.
Ans: The statement is True
The given points are A( - 1, - 2),B(4,3),C(2,5) and D( - 3,0)
Length of $AB = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
$AB = \sqrt {{{(4 + 1)}^2} + {{(3 + 2)}^2}}$
$AB = \sqrt {50} = 5\sqrt 2$
Length of $BC = \sqrt {{{(2 - 4)}^2} + {{(5 - 3)}^2}}$
$BC = \sqrt {4 + 4} = \sqrt 8 = 2\sqrt 2$
Length of $CD = \sqrt {{{( - 3 - 2)}^2} + {{(0 - 5)}^2}}$
$CD = \sqrt {25 + 25} = \sqrt {50} = 5\sqrt 2$
$DA = \sqrt {4 + 4} = \sqrt 8 = 2\sqrt 2$
$AB = CD,BC = DA$
Length of $AC = \sqrt {{{(2 + 1)}^2} + {{(5 + 2)}^2}}$
$AC = \sqrt {9 + 49} = \sqrt {58}$
Length of $BD = \sqrt {{{( - 3 - 4)}^2} + {{(0 - 3)}^2}}$
$BD = \sqrt {49 + 9} = \sqrt {58}$
$AC = BD$ (Diagonals)
Hence, $ABCD$ is a rectangle as
$AB = CD,BC = DA,AC = BD$
EXERCISE 7.3
1. Name the type of triangle formed by the points $A( - 5,6),B( - 4, - 2),C(7,5)$
Ans: ${\text{ABC}}$ is a scalene triangle.
Given vertices are $A( - 5, 6), B( - 4, - 2), C(7, 5)$
Distance formula $= \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
Distance of $AB = \sqrt {{{( - 4 - ( - 5))}^2} + {{( - 2 - 6)}^2}}$
$= \sqrt {{{(1)}^2} + {{( - 8)}^2}}$
$= \sqrt {1 + 64}$
$= \sqrt {65}$
$= \sqrt {{{(11)}^2} + {{(7)}^2}}$
$= \sqrt {121 + 49}$
$= \sqrt {170}$
Distance of $AC = \sqrt {{{(7 - ( - 5))}^2} + {{(5 - 6)}^2}}$
$= \sqrt {{{(12)}^2} + {{( - 1)}^2}}$
$= \sqrt {144 + 1}$
$= \sqrt {145}$
$AB \ne BC \ne AC$
Therefore, $ABC$ is a scalene triangle.
2. Find the points on the x-axis which are at a distance of $2\sqrt 5$ from the point $ (7, - 4)$. How many such points are there
Ans: Point are $(9, 0)$ and $(5, 0)$
Let point on $x$-axis is $(x, 0)$ $\left[ {\because {\text{ }}y is zero on - axis} \right]$
Given point $(7, - 4)$
Distance $= 2\sqrt 5$
$2\sqrt 5 = \sqrt {{{(7 - x)}^2} + {{( - 4, - 0)}^2}}$
Squaring both sides
${(2\sqrt 5 )^2} = {(7 - x)^2} + {( - 4)^2}$
$20 = 49 + {x^2} - 14x + 16$
${x^2} - 14x + 65 - 20 = 0$
${x^2} - 14x + 45 = 0$
${x^2} - 9x - 5x + 45 = 0$
$x(x - 9) - 5(x - 9) = 0$
$(x - 9)(x - 5) = 0$
$x = 9, x = 5$
Point are $(9,0)$ and $(5,0)$
Hence, two points are there.
3. What type of a quadrilateral do the points $A(2, - 2), B(7,3), C(11, - 1), D(6, - 6)$ taken in that order, form?
Ans: Rectangle
Let the points be $A(2, - 2), B(7,3), C(11, - 1), D(6, - 6)$ of a quadrilateral $ABCD$
$AB = \sqrt {{{(7 - 2)}^2} + {{(3 + 2)}^2}} = \sqrt {{5^2} + {5^2}} = \sqrt {25 + 25} = \sqrt {50}$
$BC = \sqrt {{{(7 - 11)}^2} + {{( - 1 - 3)}^2}} = \sqrt {{{(4)}^2} + {{( - 4)}^2}} = \sqrt {16 + 16} = \sqrt {32}$
$CD = \sqrt {{{(6 - 11)}^2} + {{( - 6 + 1)}^2}} = \sqrt {{{( - 5)}^2} + {{( - 5)}^2}} = \sqrt {25 + 25} = \sqrt {50}$
$DA = \sqrt {{{(6 - 2)}^2} + {{( - 6 + 2)}^2}} = \sqrt {{{(4)}^2} + {{( - 4)}^2}} = \sqrt {16 + 16} = \sqrt {32}$
$AC = \sqrt {{{(11 - 2)}^2} + {{( - 1 + 2)}^2}} = \sqrt {{{(9)}^2} + {{(1)}^2}} = \sqrt {81 + 1} = \sqrt {82}$
$BD = \sqrt {{{(6 - 7)}^2} + {{( - 6 - 3)}^2}} = \sqrt {{{(1)}^2} + {{( - 9)}^2}} = \sqrt {1 + 81} = \sqrt {82}$
$AS, AB = CD$ and $BC = DA$ and $AC = BD$
Hence, the quadrilateral is a rectangle.
4. Find the value of a, if the distance between the points $A( - 3, - 14)$ and $B(a, - 5)$ is $9 units$
Ans: $- 3$
Here, points are $A( - 3, - 14)$ and $B(a, - 5)$
Distance $= 9$
$\left( {{x_1},{y_1}} \right) = ( - 3, - 14)$
$\left( {{x_2},{y_2}} \right) = (a, - 5)$
$9 = \sqrt {{{(a + 3)}^2} + {{( - 5 + 14)}^2}}$
Squaring both sides we get
${(9)^2} = {(a + 3)^2} + {(9)^2}$
${(a + 3)^2} = 0$
$\Rightarrow a + 3 = 0$
$a = - 3$
Value of a is $- 3$
5. Find a point which is equidistant from the points $A( - 5, 4)$ and $B( - 1, 6)$? How many such points are there?
Ans: Infinite numbers of points are there
Let ${\text{P }}(x, y)$ is a point which is equidistant from point $A( - 5, 4)$ and $B( - 1, 6)$ i.e. $PA = PB$
Squaring both sides we get
$P{A^2} = P{B^2}$
${( - 5 - x)^2} + {(4 - y)^2} = {( - 1 - x)^2} + {(6 - y)^2}$
$25 + {x^2} + 10x + 16 + {y^2} - 8y = 1 + {x^2} + 2x + 36 + {y^2} - 12y$
$\left[ {Using:{{(a + b)}^2} = {a^2} + {b^2} + 2ab;{{(a - b)}^2} = {a^2} + {b^2} - 2ab} \right]$
$25 + 10x + 16 - 8y = 1 + 2x + 36 - 12y$
$10x - 8y + 41 - 2x + 12y - 37 = 0$
$8x + 4y + 4 = 0$
Dividing by 4 we get
$2x + y + 1 = 0 \ldots ..(1)$
Mid - point of $AB = \left( {\dfrac{{ - 5 - 1}}{2},\dfrac{{4 + 6}}{2}} \right)$
$= ( - 3,5)$
Put point $( - 3,5)$ in eqn. (1)
$2( - 3) + 5 + 1$
$ - 6 + 6$
$0$
Mid-point of $AB$ satisfy equation (1)
Hence, infinite numbers of points are there.
6. Find the coordinates of the point Q on the x-axis which lies on the perpendicular bisector of the line segment joining the points $ A\left( {--5,--2} \right) and B \left( {4,--2} \right)$ Name the type of triangle formed by the points Q, A and B.
Ans: $\Delta ABQ$ Is an isosceles triangle.
Use distance formula $= \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
Let $Q(x,0)$$\left[ {\because On - axis y coordinate is zero} \right]$
$Q$ Lies on the perpendicular bisector of the line AB i.e.
$AQ = BQ$
Squaring both sides
$A{Q^2} = B{Q^2}$
${(x - 5)^2} + {(0 + 2)^2} = {(x - 4)^2} + {(0 + 2)^2}$
${x^2} + 25 - 10x + 4 = {x^2} + 16 - 8x + 4$
$29 - 10x = 20 - 8x$
$29 - 20 = - 8x + 10x$
$9 = 2x$
$\dfrac{9}{2} = x$
$x = 4.5$
$\therefore$ The co-ordinate of $Q$ is $(4.5,0)$
$\because AQ = BQ$ And $Q$ lies on the perpendicular bisector of the line AB
$\therefore \Delta ABQ$ Is an isosceles triangle.
7. Find the value of $m$ if the points $A(5,1), B( - 2, - 3), C(8,2m)$ are collinear.
Ans: $m = \dfrac{{19}}{{14}}$
Given points are $A(5,1),B( - 2, - 3),C(8,2m)$
If points are collinear then the area of triangle $= 0$
$\Rightarrow 5( - 3 - 2m) - 2(2m - 1) + 8(1 + 3) = 0$
$\Rightarrow - 15 - 10m - 4m + 2 + 32 = 0$
$\Rightarrow - 14m + 19 = 0$
$\Rightarrow 14m = 19$
$\Rightarrow m = \dfrac{{19}}{{14}}$
8. If the point $A (2, - 4)$ is equidistant from $P (3, 8)$ and $Q ( - 10, y)$ , find the values of y. Also find distance PQ.
Ans: $13\sqrt 2 Units$ or$\sqrt {290} Units$
Given: Point $A (2, - 4)$ is equidistant from $P (3,8)$ and $Q ( - 10,y)$
$AP = AQ$
Square both sides
$A{P^2} = A{Q^2}$
${(3 - 2)^2} + {(8 + 4)^2} = {( - 10 - 2)^2} + {(y + 4)^2}$ (Using distance formula)
${(1)^2} + {(12)^2} = {(12)^2} + {(y)^2} + {(4)^2} + 2 \times y \times 4 \left\{ {Q{{(a + b)}^2} = {a^2} + {b^2} + 2ab} \right\}$
$1 + 144 = 144 + {y^2} + 16 + 8y$
${y^2} + 8y + 15 = 0$
${y^2} + 3y + 5y + 15 = 0$
$y \times (y + 3) + 5 \times (y + 3) = 0$
$(y + 5)(y + 3) = 0$
$y = - 5,{\text{ }}y = - 3$
Case-I when $y = - 5$ , $ PQ = \sqrt {{{( - 10 - 3)}^2} + {{( - 5 - 8)}^2}} = \sqrt {169 + 169} = 13\sqrt 2$ Units
Case-II when $y = - 3$ , $PQ = \sqrt {{{( - 10 - 3)}^2} + {{( - 3 - 8)}^2}} = \sqrt {169 + 121} = \sqrt {290}$ Units
9. Find the area of the triangle whose vertices are $( - 8, 4),( - 6, 6),( - 3, 9)$
Ans: $30{\text{ Sq}}{\text{. Units}}$
Given vertices are $( - 8, 4),( - 6, 6),( - 3, 9)$
${x_1} = - 8{x_2} = - 6{x_3} = - 3$
${y_1} = 4{y_2} = 6{y_3} = 9$
We know that area of triangle is
$= \dfrac{1}{2}[24 + 30 + 6]$
$= \dfrac{1}{2}[60]$
$= 30 Sq. Units$
10. In what ratio does the x–axis divide the line segment joining the points $( - 4, - 6)$ and $( - 1, 7)$? Find the coordinates of the point of division.
Ans: $Co - ordinate of P\left( {\dfrac{{ - 34}}{{13}},0} \right)$
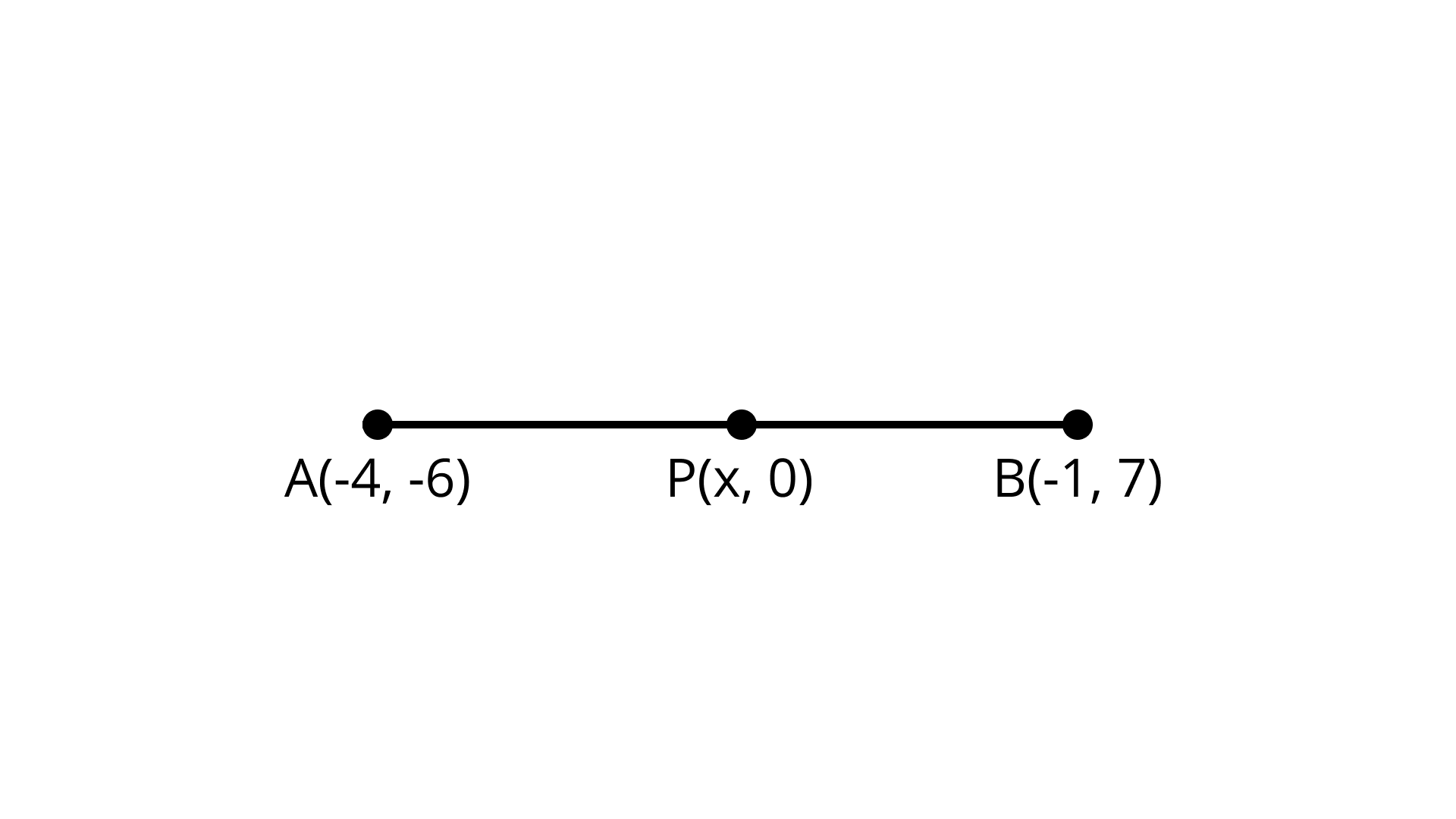
Let the point on $x$ -axis $(x,0)$ when divides the given points $( - 4, - 6)$ and $( - 1, 7)$ in the
Ratio $k:1$
$\left( {{x_1},{y_1}} \right) = A( - 4, - 6)$
$\left( {{x_2},{y_2}} \right) = B( - 1,7)$
${m_1} = k,{m_2} = 1$
Using section formula, we have
$P(x,0) = \left[ {\dfrac{{ - k - 4}}{{k + 1}},\dfrac{{7k - 6}}{{k + 1}}} \right]$
By comparing the left-hand side and the right-hand side we get
$\dfrac{{7k - 6}}{{k + 1}} = 0$
$7k - 6 = 0$
$k = \dfrac{6}{7}$
$x = \dfrac{{ - k - 4}}{{k + 1}} = \dfrac{{ - \dfrac{6}{7} - 4}}{{\dfrac{6}{7} + 1}} = \dfrac{{ - 6 - 28}}{{6 + 7}} = \dfrac{{ - 34}}{{13}}$
The required ratio is $6:7$
$Co - ordinate of P\left( {\dfrac{{ - 34}}{{13}},0} \right)$
11. Find the ratio in which the point $P\left( {\dfrac{3}{4},\dfrac{5}{{12}}} \right)$ divides the line segment joining the points $ A\left( {\dfrac{1}{2},\dfrac{3}{2}} \right)$ and $B (2, - 5)$.
Ans: $1:5$
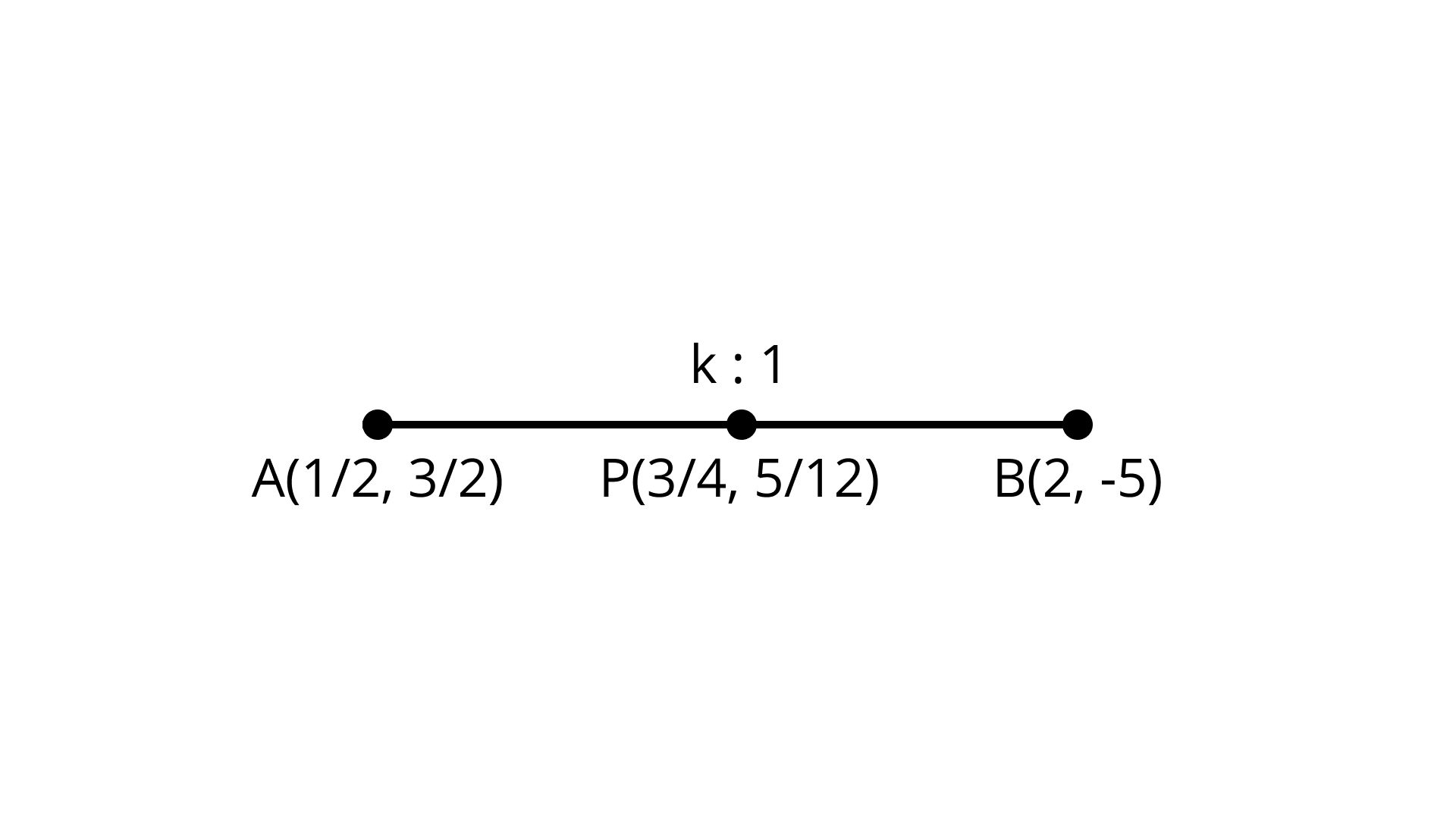
Let the point $P\left( {\dfrac{3}{4},\dfrac{5}{{12}}} \right)$ divides the line segment joining the joining the points $A\left( {\dfrac{1}{2},\dfrac{3}{2}} \right)$ and
$B(2, - 5)$ In the ratio $k:1$.
$\left( {{x_1},{y_1}} \right) = \left( {\dfrac{1}{2},\dfrac{3}{2}} \right)$
$\left( {{x_2},{y_2}} \right) = (2, - 5)$
${m_1} = k,{m_2} = 1$
Using section formula, we have
$\left( {\dfrac{3}{4},\dfrac{5}{{12}}} \right) = \left[ {\dfrac{{2k + 1/2}}{{k + 1}},\dfrac{{ - 5k + 3/2}}{{k + 1}}} \right]$
$\left( {\dfrac{3}{4},\dfrac{5}{{12}}} \right) = \left[ {\dfrac{{4k + 1}}{{2k + 1}},\dfrac{{ - 10k + 3}}{{2k + 2}}} \right]$
$\dfrac{{4k + 1}}{{2k + 1}} = \dfrac{3}{4},\dfrac{{ - 10k + 3}}{{2k + 2}} = \dfrac{5}{{12}}$
$16k + 4 = 6k + 6 - 120k + 36 = 10k + 10$
$16k - 6k = 6 - 4 - 130k = - 26$
$k = \dfrac{2}{{10}} = \dfrac{1}{5}$
Therefore the required ratio is $1:5$
12. If $P (9a - 2, - b)$ divides line segment joining $A (3a + 1, - 3)$ and $B (8a,5)$ in the ratio $3:1$, find the values of a and b.
Ans: $a = 1$ and $b = - 3$
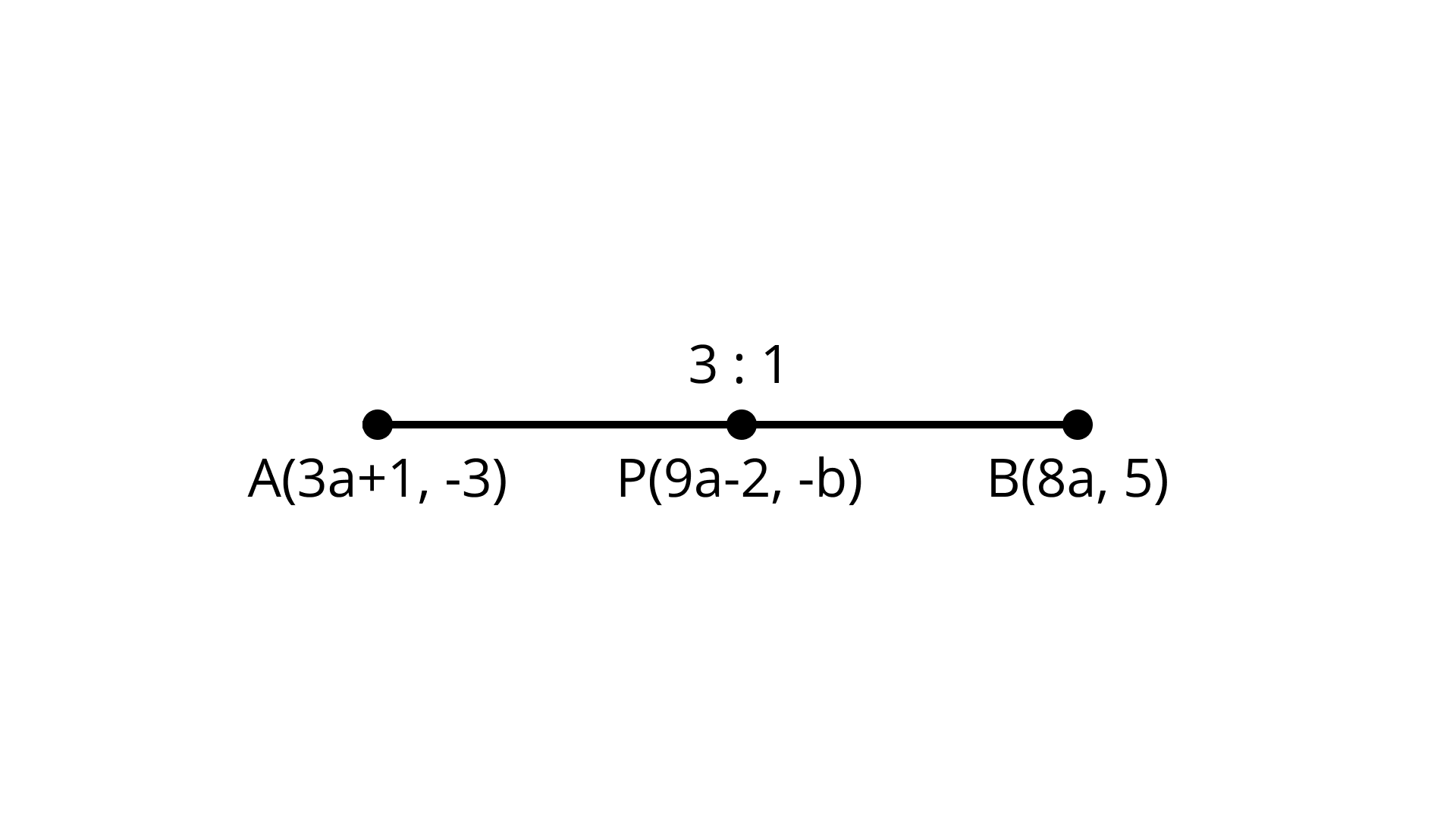
Point $P (9a - 2, - b)$ divides line segment joining the points $A (3a + 1, - 3)$ and $B (8a,5)$
In ration $3:1$
$\left( {{x_1},{y_1}} \right) = (3a + 1, - 3)$
$\left( {{x_2},{y_2}} \right) = (8a,5)$
${m_1} = 3,{m_2} = 1$
Using section formula, we have
$(9a - 2, - b) = \left[ {\dfrac{{24a + 3a + 1}}{4},\dfrac{{15 - 3}}{4}} \right]$
$(9a - 2, - b) = \left[ {\dfrac{{27a + 1}}{4},\dfrac{{12}}{4}} \right]$
Equate left-hand side and the right-hand side we get
$9a - 2 = \dfrac{{27a + 1}}{4}, - b = \dfrac{{12}}{4}$
$36a - 8 = 27a + 1, - b = 3$
$9a = 9,b = - 3$
$a = \dfrac{9}{9}$
$a = 1$ And $b = - 3$
13. If $P(a, b)$ is the mid-point of the line segment joining the points $A(10, - 6)$ and $B(k, 4)$ and $a - 2b = 18$ , find the value of k and the distance AB.
Ans: $2\sqrt {61}$
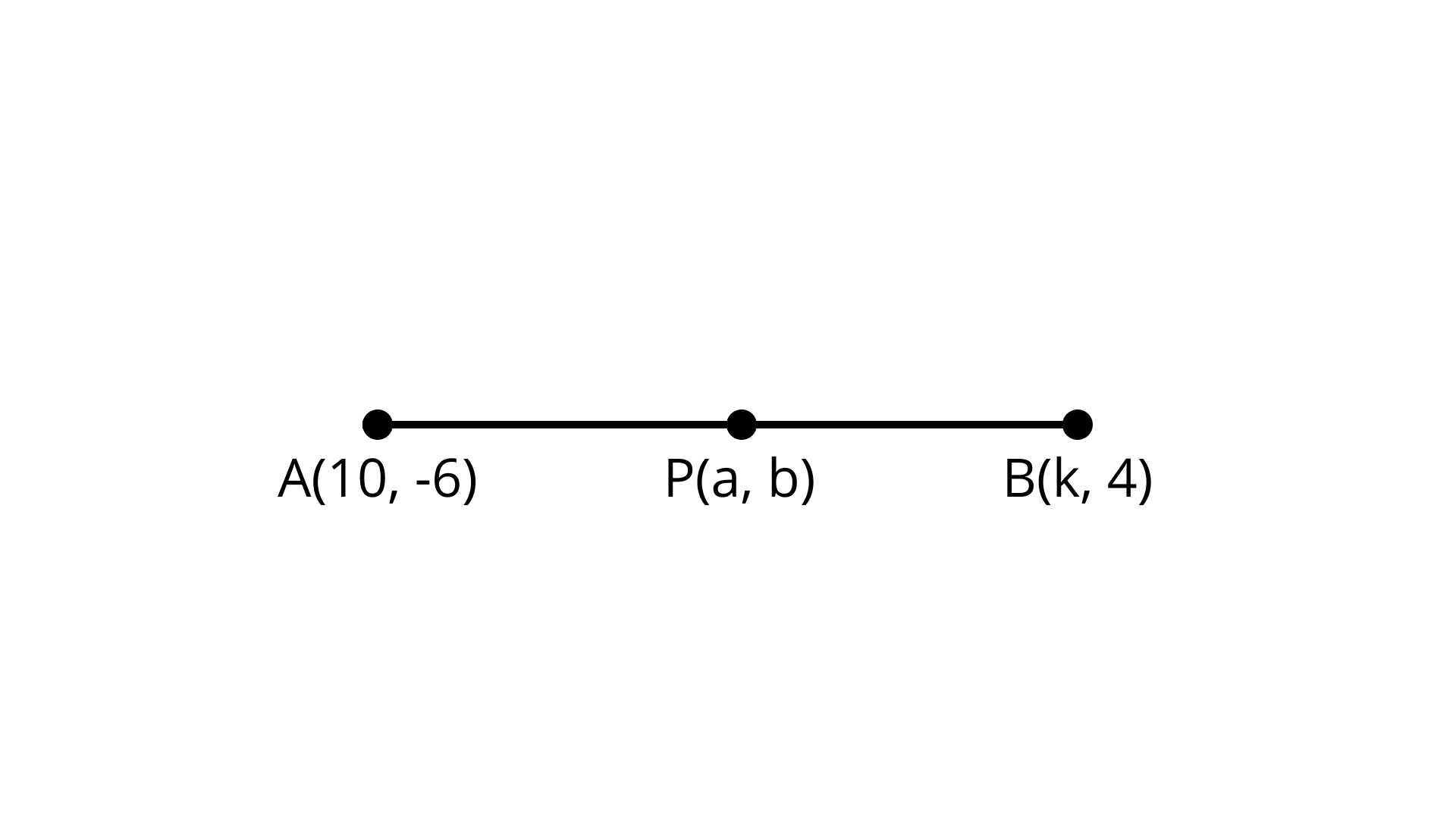
Mid - point formula: $x = \dfrac{{{x_1} + {x_2}}}{2},y = \dfrac{{{y_1} + {y_2}}}{2}$
Point $P(a, b)$ divide $A(10, - 6)$ and $B(k, 4)$ in two equal parts.
$a = \dfrac{{10 + k}}{2},b = \dfrac{{ - 6 + 4}}{2} = \dfrac{{ - 2}}{2} = - 1$
Given: $a - 2b = 18$
Put $b = - 1$
$a - 2( - 1) = 18$
$a = 18 - 12$
$a = 16$
Now, $a = \dfrac{{10 + k}}{2}$
$16 = \dfrac{{10 + k}}{2}$
$32 = 10 + k$
$32 - 10 = k$
$22 = k$
$\therefore A(10, - 6), B(22, 4)$
$AB = \sqrt {{{(22 - 10)}^2} + {{(4 + 6)}^2}}$
$= \sqrt {{{(12)}^2} + {{(10)}^2}}$
$= \sqrt {144 + 100}$
$= \sqrt {244}$
$= 2\sqrt {61}$
14: The Centre of a circle is $A(2a, a - 7)$. Find the values of a if the circle passes through the point $B(11, - 9)$ and has diameter $10\sqrt 2$ units.
Ans: $a = 5, 3$
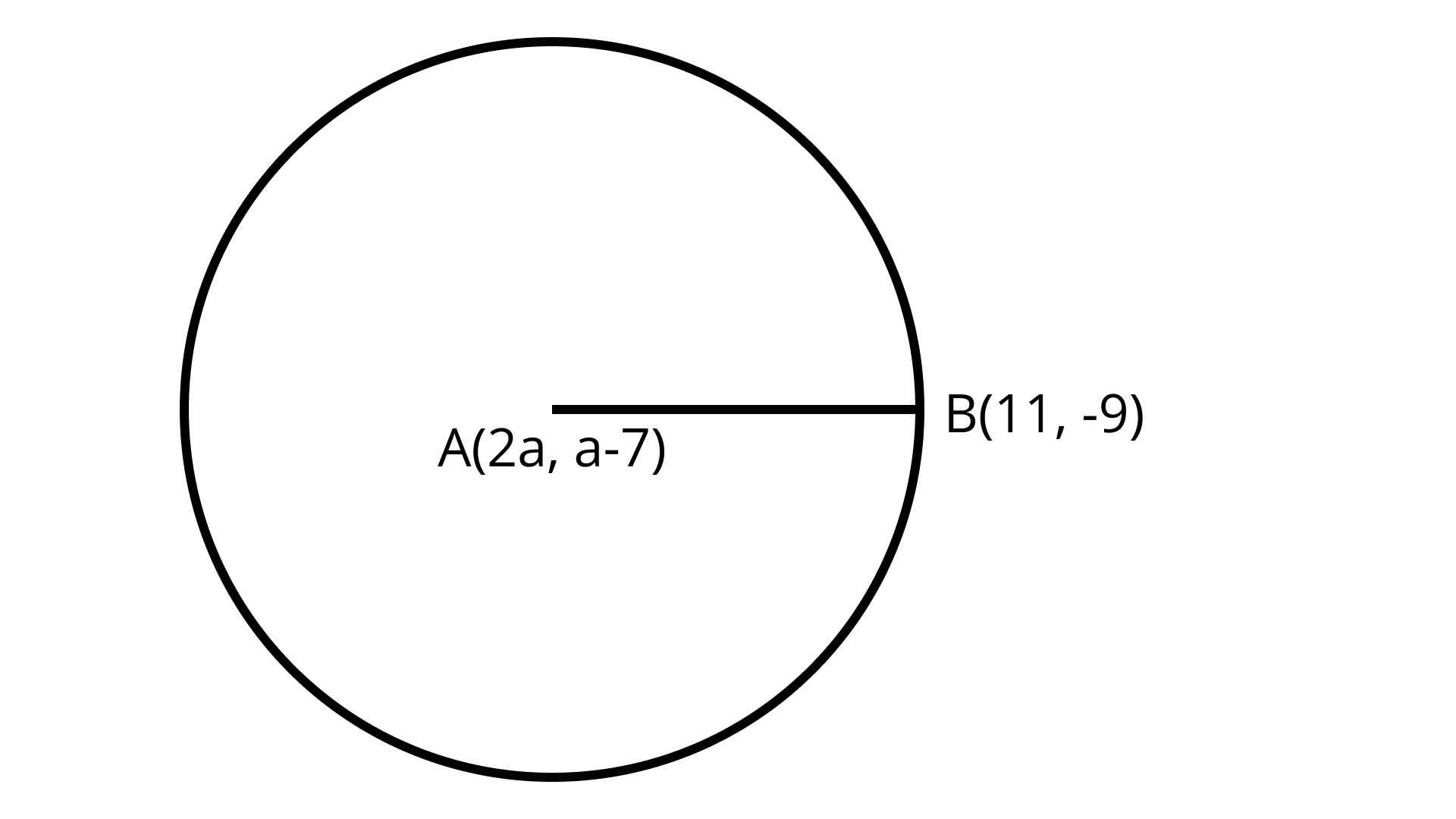
Distance formula $= \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
Given points area $A(2a, a - 7)$ and $B(11, - 9)$
Diameter $= 10 \sqrt 2$
Radius $= \dfrac{{10\sqrt 2 }}{2} = 5\sqrt 2$
Distance $= 5\sqrt 2$
$\left( {{x_1},{y_1}} \right) = (2a, a - 7)$
$\left( {{x_2},{y_2}} \right) = (11, - 9)$
$= \sqrt {{{(11 - 2a)}^2} + {{( - 9 - a + 7)}^2}} = (5\sqrt 2 )$
Squaring both sides ${(11 - 2a)^2} + {( - 2 - a)^2} = {(5\sqrt 2 )^2}$
$121 + 4{a^2} - 44a + 4 + {a^2} + 4a = 50$
$502 - 40a + 125 - 50 = 0$
$5{a^2} - 40a + 75 = 0$
Dividing by 5 we get
${a^2} - 8a + 15 = 0$
${a^2} - 5a - 3a + 15 = 0$
$a(a - 5) - 3(a - 5) = 0$
$(a - 5)(a - 3) = 0$
$a = 5, 3$
15. The line segment joining the points $A(3, 2)$ and $B(5, 1)$ is divided at the point P in the ratio 1:2 and it lies on the line $3x - 18y + k = 0$. Find the value of k.
Ans: $k = 19$
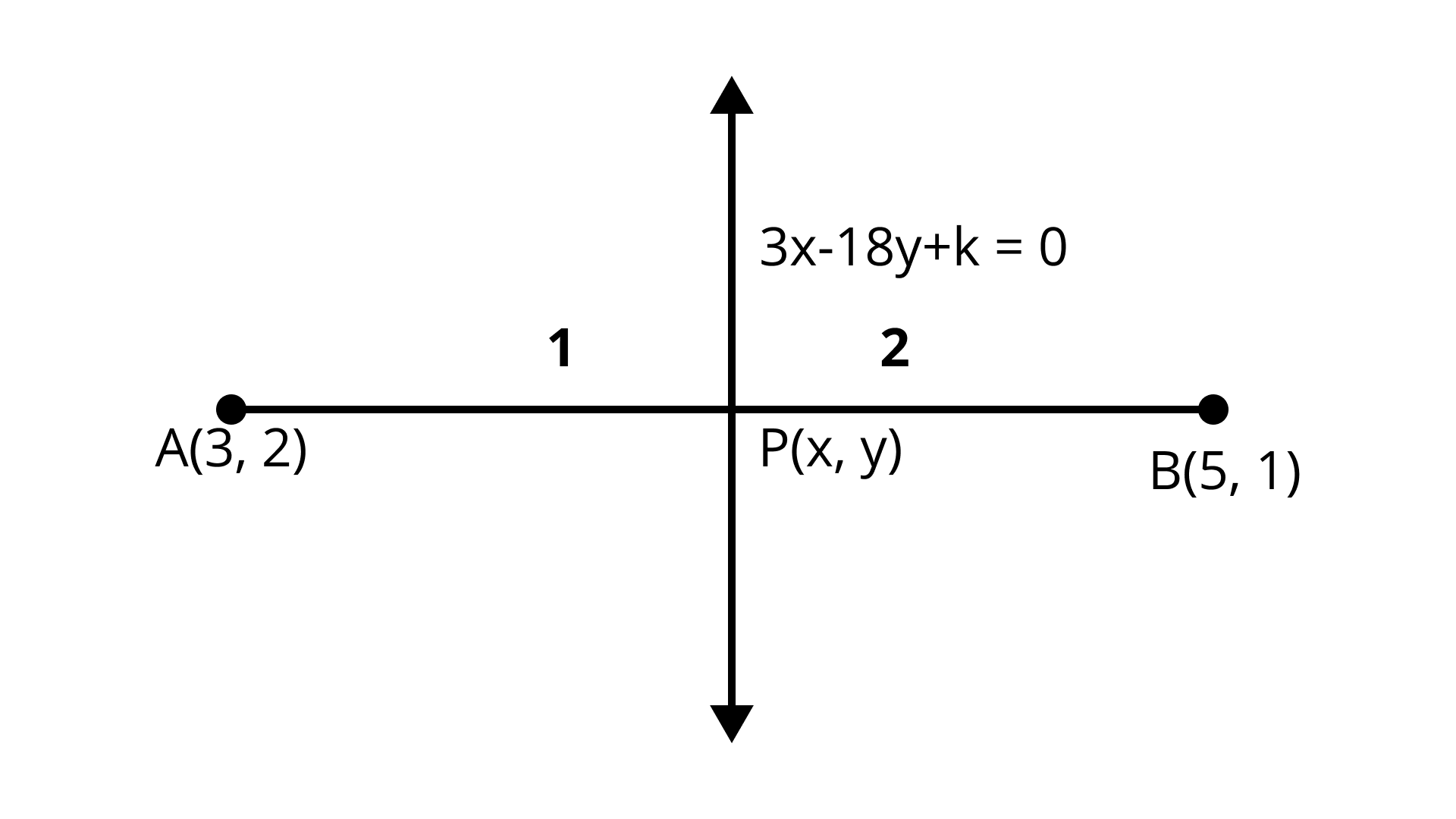
Here points $A(3, 2)$ and $B(5, 1)$ is divided at the point $P$ in the ratio 1:2
$\left( {{x_1},{y_1}} \right) = (3,2),\left( {{x_2},{y_2}} \right) = (5, 1)$
${m_1} = 1,{m_2} = 2$
By section formula we have
$P(x,y) = \left[ {\dfrac{{1 \times 5 + 2 \times 3}}{{1 + 2}},\dfrac{{1 \times 1 + 2 \times 2}}{{1 + 2}}} \right]$
$= \left[ {\dfrac{{5 + 6}}{3},\dfrac{{1 + 4}}{3}} \right]$
$= \left[ {\dfrac{{11}}{3},\dfrac{5}{3}} \right]$
Line is $3x - 18y + k = 0 \ldots \ldots (1)$
Put point $P\left( {\dfrac{{11}}{3},\dfrac{5}{3}} \right)$ in $(1)$
$Put x = \dfrac{{11}}{3},y = \dfrac{5}{3}$
$3\left( {\dfrac{{11}}{3}} \right) - 18\left( {\dfrac{5}{3}} \right) + k = 0$
$11 - 30 + k = 0$
$ - 19 + k = 0$
$k = 19$
16. If $D\left( {\dfrac{{ - 1}}{2},\dfrac{5}{2}} \right),E\left( {7,3} \right) and F\left( {\dfrac{7}{2},\dfrac{7}{2}} \right)$ dare the midpoints of sides of $\Delta ABC$ find the area of the $\Delta ABC$.
Ans: $11Sq. Units$ Units
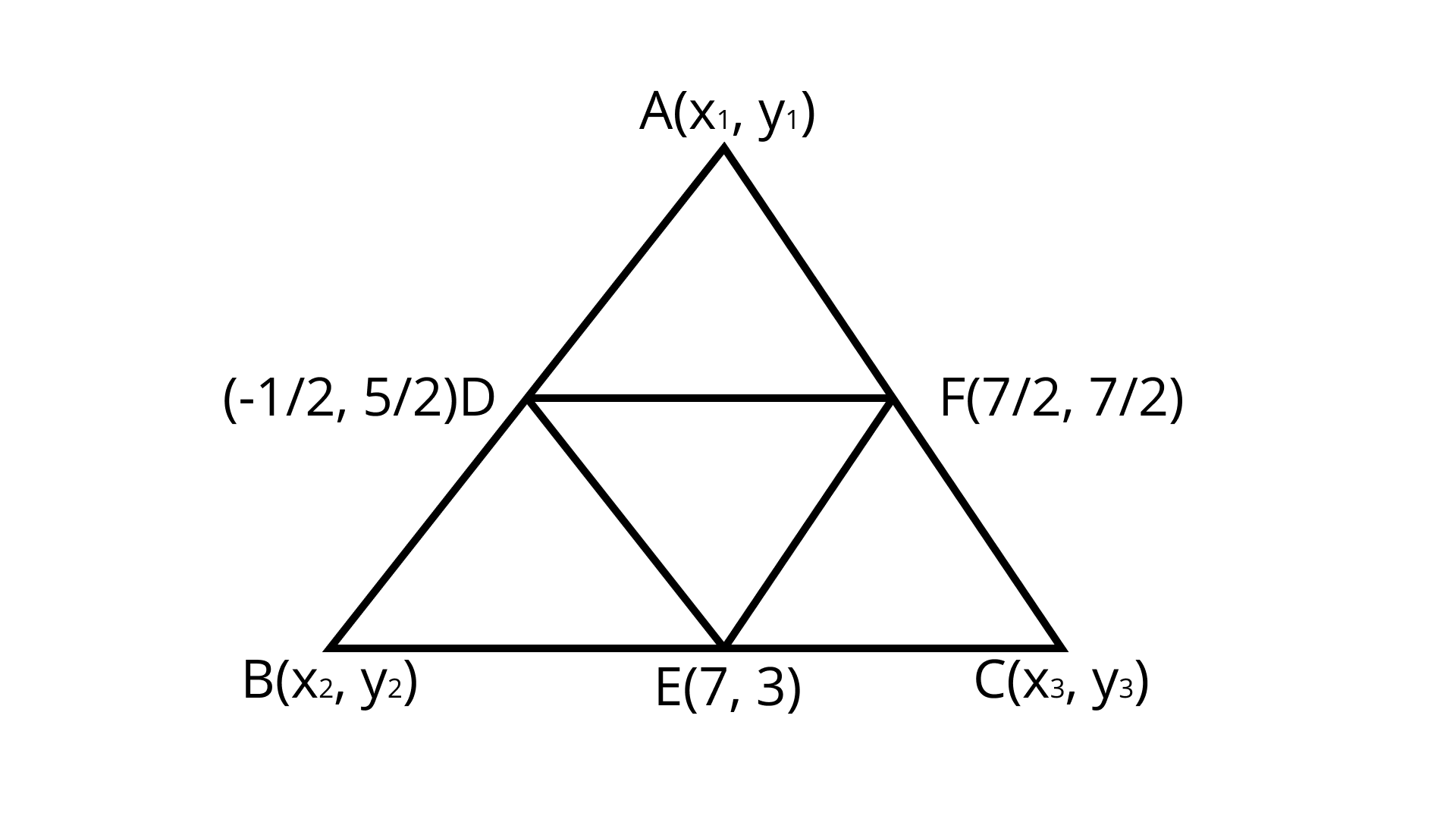
$D$ Is mid-point of $AB$ using mid-point formula:
$- \dfrac{1}{2} = \dfrac{{{x_1} + {x_2}}}{2},\dfrac{5}{2} = \dfrac{{{y_1} + {y_2}}}{2}$
${x_1} + {x_2} = - 1 \ldots \ldots $ (1)
$5 = {y_1} + {y_2} \ldots (2)$
${\text{E}}$ Is mid-point of BC using mid-point formula:
$\dfrac{{{x_2} + {x_3}}}{2} = 7,\dfrac{{{y_2} + {y_3}}}{2} = 3$
${x_2} + {x_3} = 14 \ldots \ldots (3)$
${y_2} + {y_3} = 6 \ldots .(4)$
${\text{F}}$ is mid-point of ${\text{AB}}$ using mid-point formula:
$\dfrac{{{x_1} + {x_3}}}{2} = \dfrac{7}{2},\dfrac{{{y_1} + {y_3}}}{2} = \dfrac{7}{2}$
${x_1} + {x_3} = 7 \ldots .(5)$
${y_1} + {y_3} = 7 \ldots \ldots (6)$
Simplifying the above equations for values of ${x_1},{y_1},{x_2},{y_2},{x_3}$ and ${y_3}$
${x_1} + {x_2} = - 1$
${x_3} + {x_3} = 14$ {Using $(1)$ and $(3)\}$
${x_1} - {x_3} = - 15 \ldots ..\left( 7 \right)$
Adding equation (5) and (7)
$2{x_1} = - 8$
${x_1} = - 4$
Put ${x_1} = 4$ in (1) we
$- 4 + {x_2} = - 1$
${x_2} = - 1 + 4 = 3$
Put ${x_2} = 3$ in (3)
$3 + {x_3} = 14$
${x_3} = 11$
Using equation (4) from equation (4)
${y_1} - {y_3} = --1 .....(8)$
Adding equation (6) and (8)
$2{y_1} = 6$
${y_1} = 3$
Put ${y_1} = 3$ in eqn. (2)
$5 - 3 = {y_2}$
$2 = {y_2}$
Put ${y_2} = 2$ in eqn. (4)
$2 + {y_3} = 6$
${y_3} = 6 - 2$
${y_3} = 4$
Hence, ${x_1} = - 4$ y $1 = 3$
${x_2} = 3{y_2} = 2$
${x_3} = 11{y_3} = 4$
$A = \left( {{x_1},{y_1}} \right) = ( - 4,3),B = \left( {{x_2},{y_2}} \right) = (3,2),C = \left( {{x_3},{y_3}} \right) = (11,4)$
$= \dfrac{1}{2}[( - 4)( - 2) + 3(1) + 11(1)]$
$= \dfrac{1}{2}[8 + 3 + 11]$
$= \dfrac{1}{2}[22]$
$= 11 Sq.Units$
17. The points $A\left( {2,9} \right), B\left( {a,5} \right), C \left( {5,5} \right)$ are the vertices of a $\Delta ABC$ right angled at B. Find the values of a and hence the area of $\Delta ABC$
Ans: $8 Sq. Units$
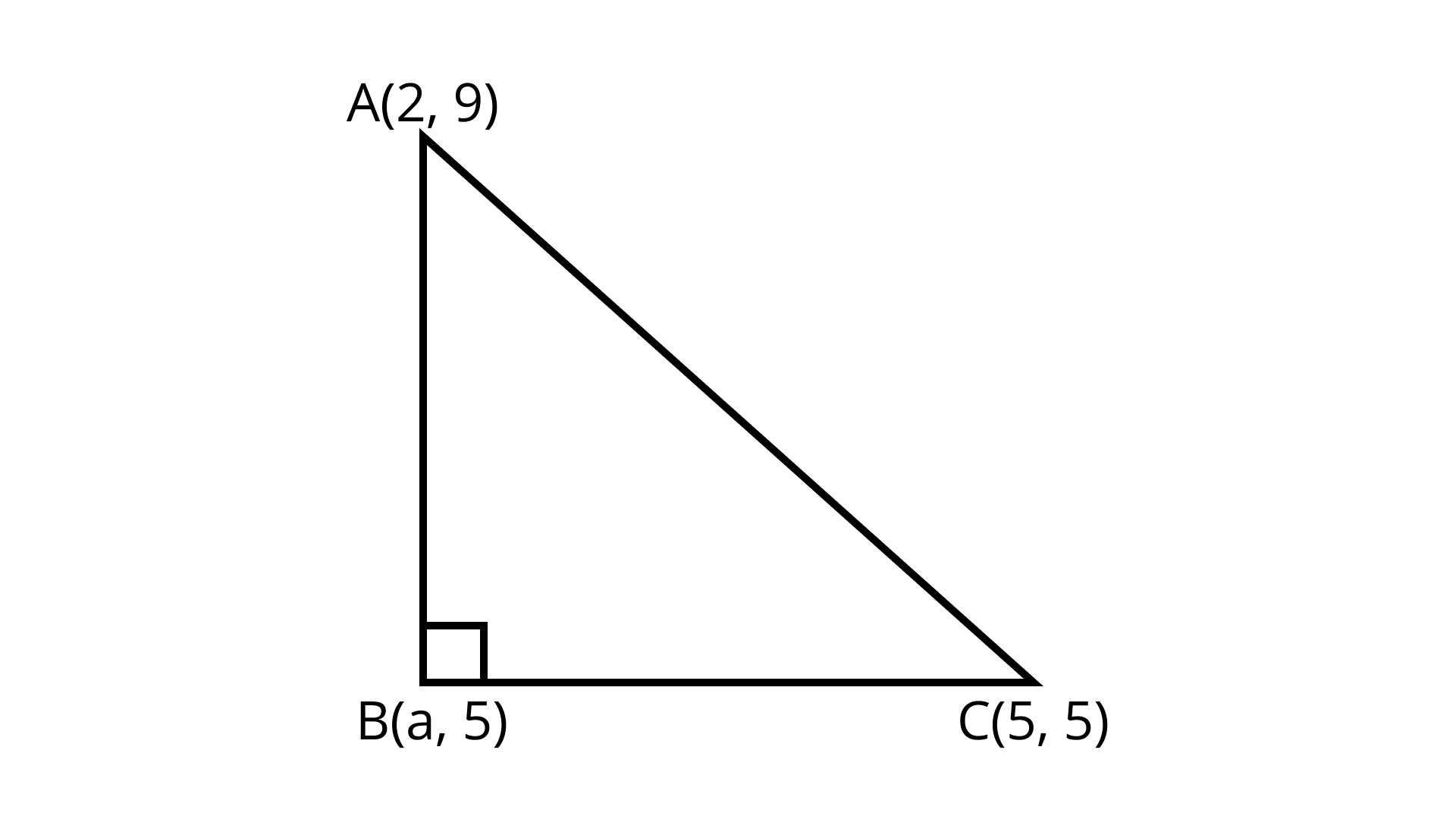
Distance formula $= \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
$\Delta ABC$ is a right angle triangle by using Pythagoras theorem
${(AC)^2} = {(BC)^2} + {(AB)^2}$
$\left[ {{{(5 - 2)}^2} + {{(5 - 9)}^2}} \right] = \left[ {{{(2 - a)}^2} + {{(9 - 5)}^2}} \right] + \left[ {{{(a - 5)}^2} + {{(5 + 5)}^2}} \right]$
${(3)^2} + {( - 4)^2} = 4 + {a^2} - 4a + {(4)^2} + {a^2} + 25 - 10a$
$9 + 16 = 4 + {a^2} - 4a + 16 + {a^2} + 25 - 10a$
$25 = 2{a^2} - 14a + 45$
$2{a^2} - 14a + 45 - 25 = 0$
$2{a^2} - 14a + 20 = 0$
Dividing by 2 we have
${a^2} - 7a + 10 = 0$
${a^2} - 5a - 2a + 10 = 0$
$a(a - 5) - 2(a - 5) = 0$
$(a - 5)(a - 2) = 0$
$a = 5,a = 2$
$a = 5$ Is not possible because if $a = 5$ then point $B$ and $C$ coincide.
$\therefore a = 2$
$= \dfrac{1}{2}[2(5 - 5) + 2(5 - 9) + 5(9 - 5)]$
$= \dfrac{1}{2}[0 - 8 + 20]$
$= \dfrac{1}{2}[16]$
$= 8 Sq. Units$
18. Find the coordinates of the point R on the line segment joining the points $P\left( {--1,3} \right)$ and $Q\left( {2,5} \right)$ such that $PR = \dfrac{3}{5}PQ$
Ans: $\left( {\dfrac{4}{5},\dfrac{{21}}{5}} \right)$
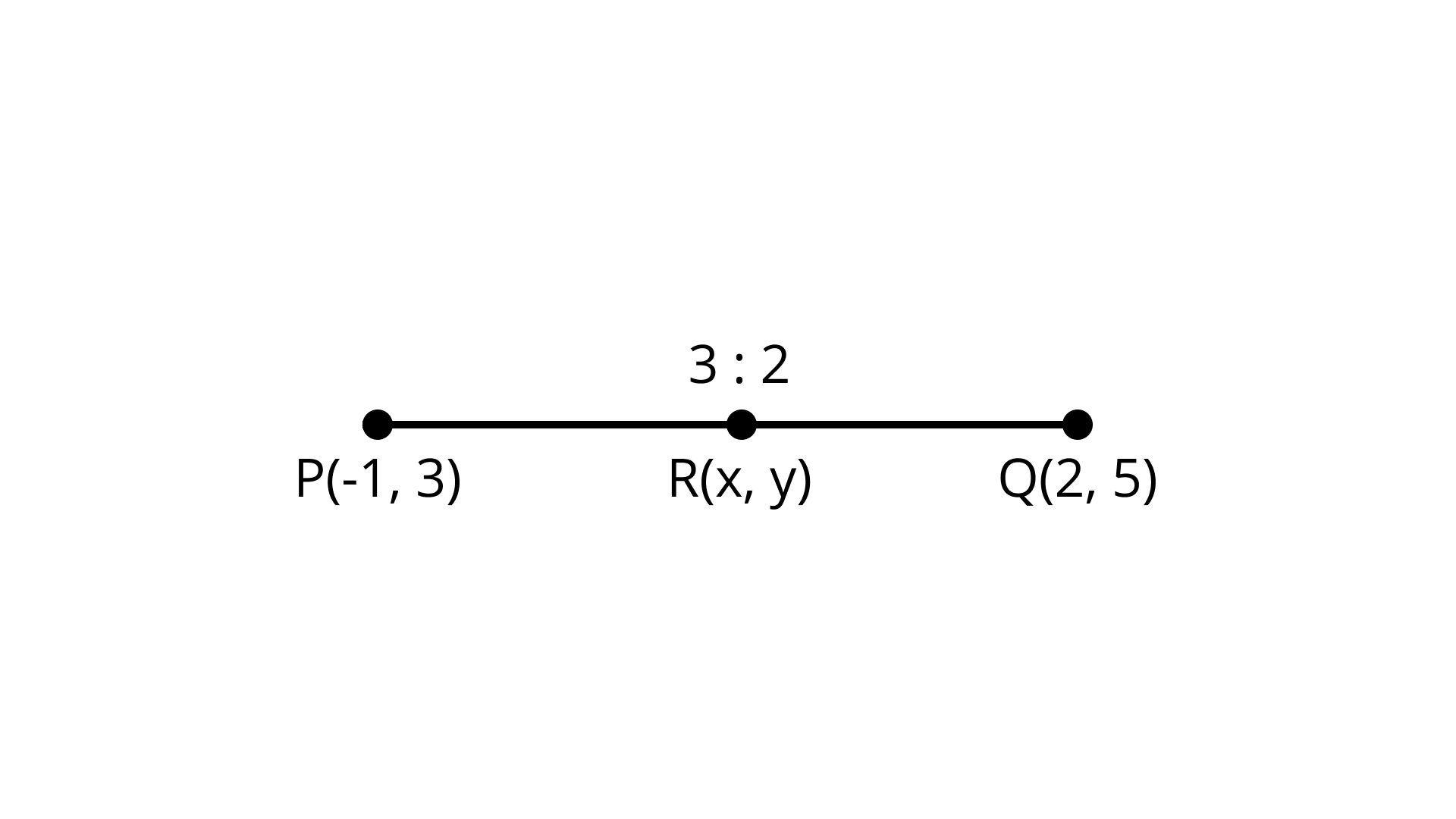
According to question let $R = (x,y)$ and $PR = \dfrac{3}{5}PQ$
$\dfrac{{PQ}}{{PR}} = \dfrac{3}{5}$
${\text{R}}$ Lies on $PQ \therefore {\text{ }}PQ = PR + RQ$
$\dfrac{{PR + PQ}}{{PR}} = \dfrac{5}{3}$
On dividing separately we get $1 + \dfrac{{RQ}}{{PR}} = \dfrac{5}{3}$
$\dfrac{{RQ}}{{PR}} = \dfrac{5}{3} - 1 = \dfrac{2}{3}$
$\Rightarrow PR:RQ = 3:2$
Hence, $R$ divides PQ in ratio 3: 2 using section formula we have
$\left( {{x_1},{y_1}} \right) = ( - 1, 3)$
$\left( {{x_2},{y_2}} \right) = (2, 5)$
${m_1} = 3,{m_2} = 2$
$R(x,y) = \left( {\dfrac{{6 - 2}}{5},\dfrac{{15 + 6}}{5}} \right)$
$R(x,y) = \left( {\dfrac{4}{5},\dfrac{{21}}{5}} \right)$
Here co- ordinates of ${\text{R}}$ is $\left( {\dfrac{4}{5},\dfrac{{21}}{5}} \right)$
19. Find the values of k if the points $A(k + 1, 2k), B(3k, 2k + 3)$ and $C(5k - 1, 5k)$are collinear.
Ans: $2,\dfrac{1}{2}$
If points $A(k + 1, 2k),B(3k, 2k + 3)$ and $C(5k - 1, 5k)$ are collinear then area of triangle is equal to zero
$[(k + 1)(2k + 3 - 5k) + 3k(5k - 2k) + (5k - 1)(2k - 2k - 3)] = 0$
$[(k + 1)(3 - 3k) + 3k(3k) + 5(k - 1)( - 3)] = 0$
$\left[ {3k - 3{k^2} + 3 - 3k + 9{k^2} - 15k + 3} \right] = 0$
$6{k^2} - 15k + 6 = 0$
$6{k^2} - 12k - 3k + 6 = 0$
$6k(k - 2) - 3(k - 2) = 0$
$(k - 2)(6k - 3)$
$k = 2,k = \dfrac{3}{6}$
$= \dfrac{1}{2}$
Hence, values of ${\text{k}}$ are $2,\dfrac{1}{2}$
20. Find the ratio in which the line $2x + 3y - 5 = 0$ divides the line segment joining the points $A(8, - 9)$ and $B(2,1)$. Also find the coordinates of the point of division.
Ans: $P\left( {\dfrac{8}{3},\dfrac{{ - 1}}{9}} \right)$
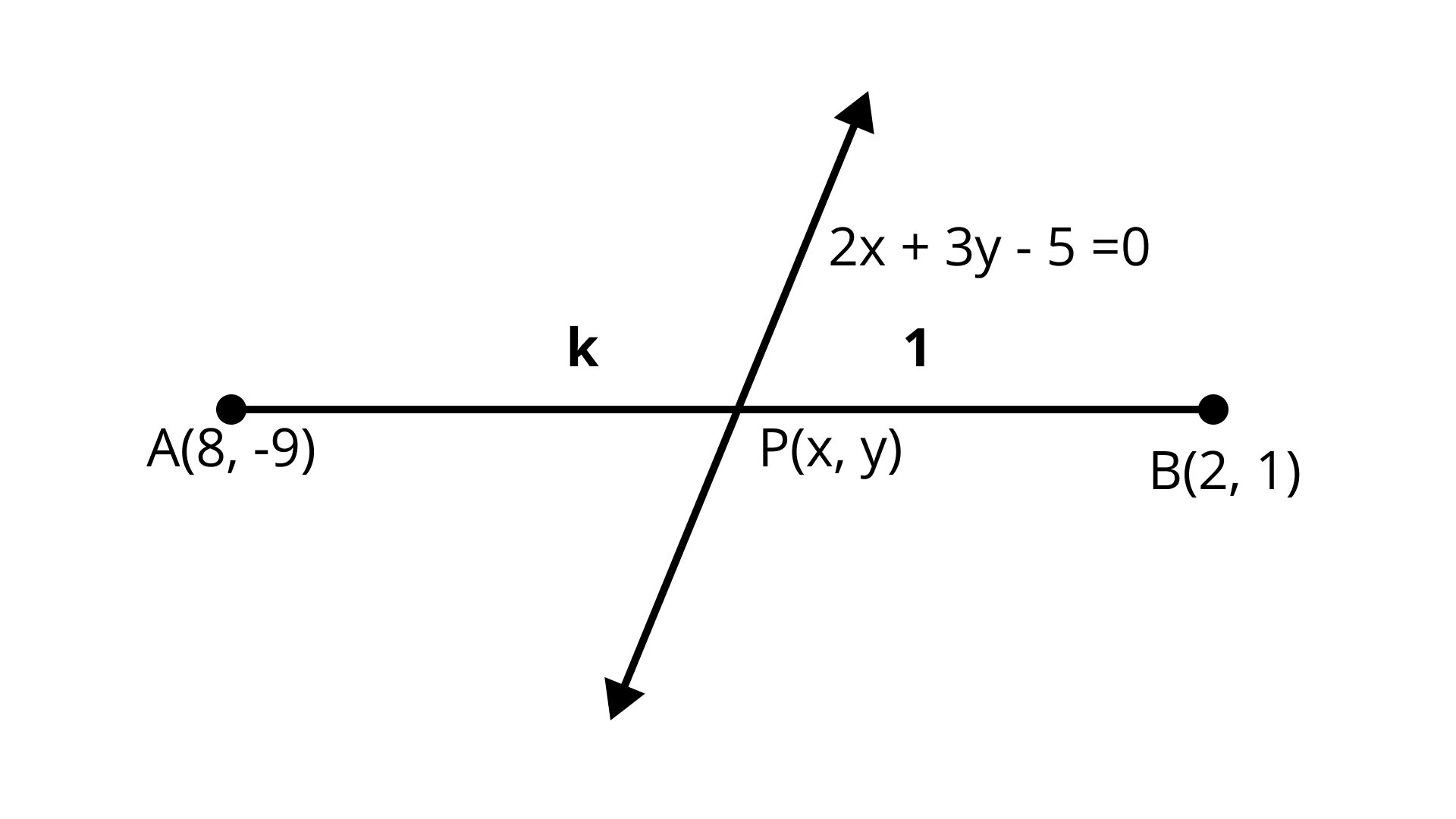
Let point $P(x, y)$ divides the line segment joining the points $A(8, - 9)$ and $B(2, 1)$ in ratio $k:1$
$\left( {{x_1},{y_1}} \right) = (8, - 9)$
$\left( {{x_2},{y_2}} \right) = (2,1)$
${m_1}:{m_2} = k:1$
Using section formula we have $P(x,y) = \left[ {\dfrac{{2k + 8}}{{k + 1}},\dfrac{{k - 9}}{{k + 1}}} \right]$
Given equation is $2x + 3y - 5 = 0 \ldots (2)$
Put values of $x$ and $y$ in eqn. (2) $2\left[ {\dfrac{{2k + 8}}{{k + 1}}} \right] + 3\left[ {\dfrac{{k - 9}}{{k + 1}}} \right] - 5 = 0$
$2(2k + 3) + 3(k - 9) - 5(k + 1) = 0$
$4k + 16 + 3k - 27 - 5k - 5 = 0$
$2k - 16 = 0$
$k = 8$
Hence, P divides the line in ration $8:1$
put ${\text{k}} = 5$ in eqn. (1)
$(x, y) = \left[ {\dfrac{{2(8)}}{{8 + 1}},\dfrac{{8 - 9}}{{8 + 1}}} \right]$
Required point is $P\left( {\dfrac{8}{3},\dfrac{{ - 1}}{9}} \right)$
EXERCISE 7.4:
1. If $( - 4, 3)$ and $(4, 3)$ are two vertices of an equilateral triangle, find the coordinates of the third vertex, given that the origin lies in the interior of the triangle.
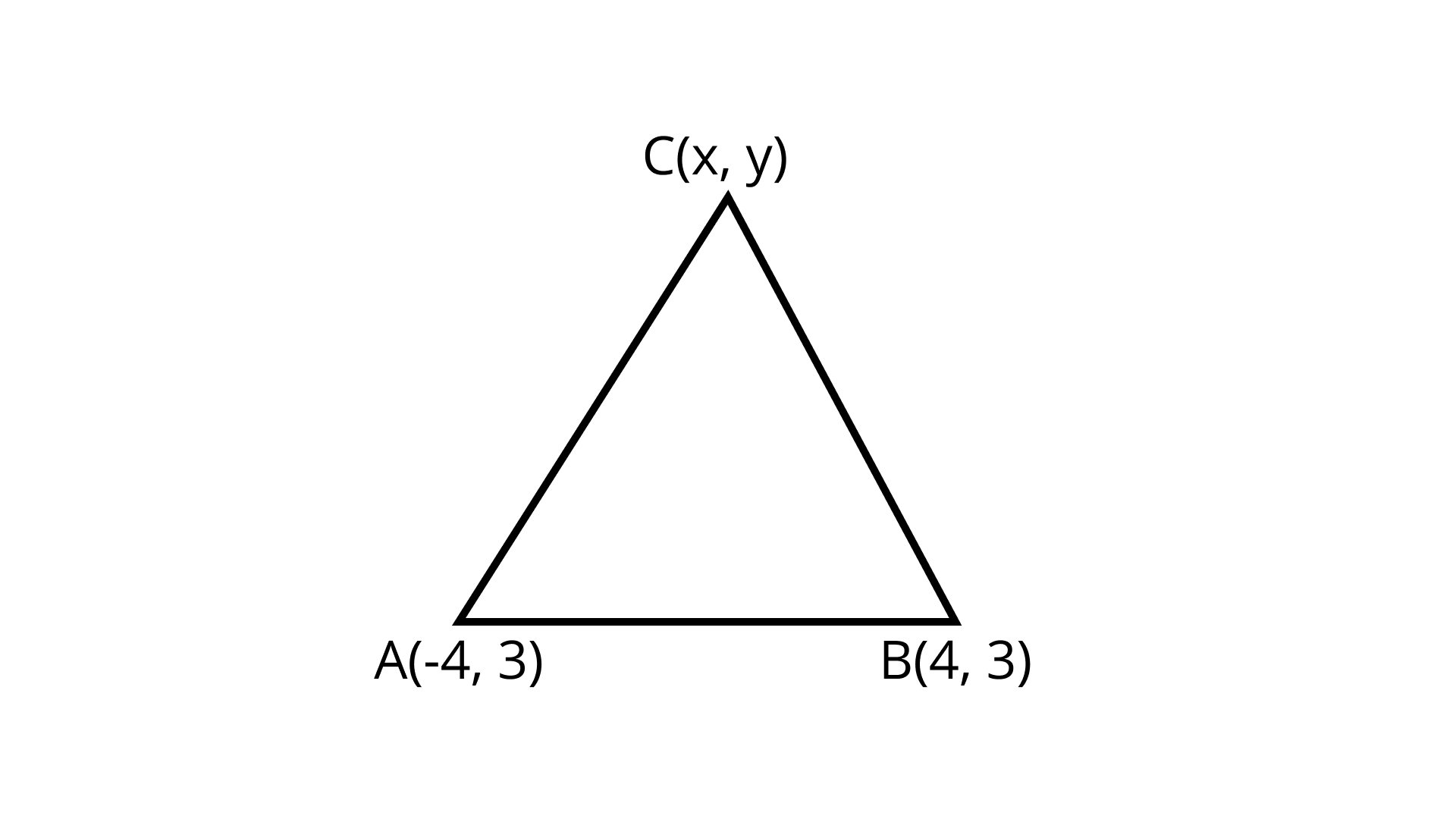
Ans: $\left( {0,3 - 4\sqrt 3 } \right)$
In equilateral triangle $AB = BC = AC$
$AC = \sqrt {{{(x + 4)}^2} + {{(y - 3)}^2}}$
$AC = \sqrt {{x^2} + 16 + 8x + {y^2} + 9 - 6y}$
$\left( {\because {\text{ }}{{(a + b)}^2} = {a^2} + {b^2} + 2ab{\text{and}}\left[ {{{(a - b)}^2} = {a^2} + {b^2} - 2ab} \right]} \right)$
$BC = \sqrt {{{(x - 4)}^2} + {{(y - 3)}^2}}$
$BC = \sqrt {{x^2} + 16 - 8x + {y^2} + 9 - 6y}$ $\left( {\because {{(a - b)}^2} = {a^2} + {b^2} - 2ab} \right)$
${\text{AC}} = {\text{BC}}$
$\sqrt {{x^2} + 16 + 8x + {y^2} + 9 - 6y} = \sqrt {{x^2} + 16 - 8x + {y^2} + 9 - 6y}$
Squaring both side
$8x + 8x = 0$
$16x = 0$
$x = 0$
$C = (0,y)$
Length of $AB = \sqrt {{{(4 + 4)}^2} + {{(3 - 3)}^2}}$
$AB = \sqrt {{{(8)}^2}} = 8$
$AC = AB$
$\sqrt {{x^2} + 16 + 8x + {y^2} + 9 - 6y} = 8$
Put$x = 0$, squaring both side
$0 + 16 + 0 + {y^2} + 9 - 6y = 64$
${y^2} - 6y + 25 - 64 = 0$
${y^2} - 6y - 39 = 0$
$y = \dfrac{{6 \pm \sqrt {36 + 156} }}{2}$
$y = \dfrac{{6 - 8\sqrt 3 }}{2}$ (For origin in the interior we take the only term with negative sign)
$y = 3 - 4\sqrt 3$
2. $A(6,1),B(8,2)$ and $C(9,4)$ are three vertices of a parallelogram $ABCD$. If $E$ is the midpoint of $DC$ , find the area of $\Delta ADE$.
Ans: $\dfrac{3}{4}sq \times units$
Distance formula $= \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
The given points $A(6,1), B(8,2)$ and $C(9,4)$ let $D(x,y)$
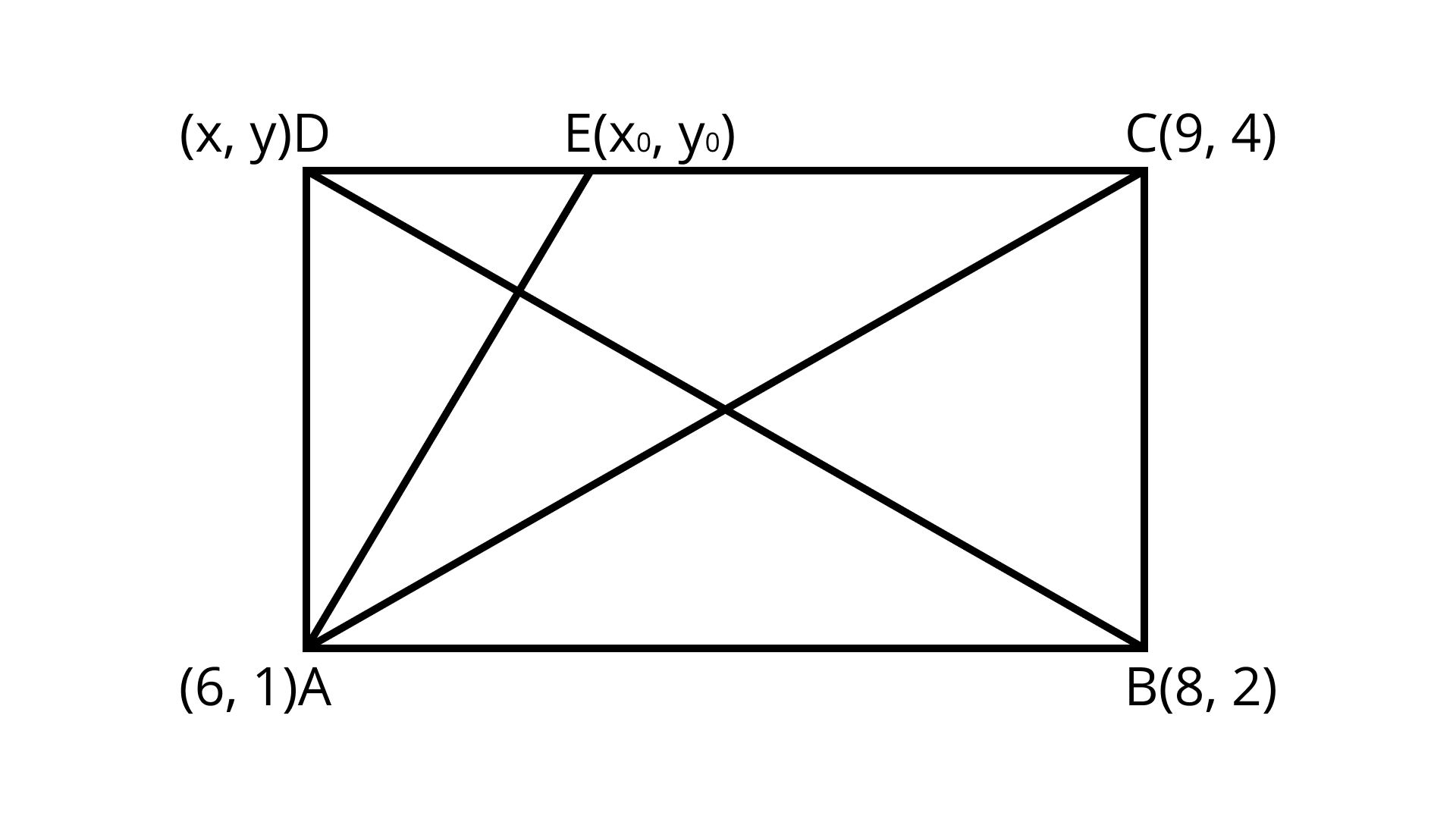
As the diagonal of a parallelogram bisect each other.
Here mid-point of ${\text{AC}} = $ mid-point of BD
$\left( {\dfrac{{6 + 9}}{2},\dfrac{{1 + 4}}{2}} \right) = \left( {\dfrac{{8 + x}}{2},\dfrac{{2 + y}}{2}} \right)$
$\left( {\dfrac{{15}}{2},\dfrac{5}{2}} \right) = \left( {\dfrac{{8 + x}}{2},\dfrac{{2 + y}}{2}} \right)$
$\dfrac{{15}}{2} = \dfrac{{8 + x}}{2}\dfrac{{2 + y}}{2} = \dfrac{5}{2}$
$x = 7y = 3$
$D(7,3)$
E is the mid-point of CD
Let $E\left( {{x_0},{y_0}} \right)$
$\left( {{x_0},{y_0}} \right) = \left( {\dfrac{{7 + 9}}{2},\dfrac{{3 + 4}}{2}} \right)$
$\left( {{x_0},{y_0}} \right) = \left( {\dfrac{{16}}{2},\dfrac{2}{7}} \right)$
$E = \left( {8,\dfrac{7}{2}} \right)$
Area of $\Delta ADE = \dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right]$
$= \dfrac{1}{2}\left[ {6\left( {\dfrac{7}{2} - 3} \right) + 8(3 - 1) + 7\left( {1 - \dfrac{7}{2}} \right)} \right]$
$= \dfrac{1}{2}\left[ {6 \times \dfrac{1}{2} + 8 \times 2 + 7 \times \dfrac{{ - 5}}{2}} \right]$
$= \dfrac{1}{2}\left[ {3 + 16 - \dfrac{{35}}{2}} \right]$
$= \dfrac{1}{2}\left[ {\dfrac{{6 + 32 - 35}}{2}} \right]$
Area of $\Delta ADE = \dfrac{1}{2} \times \dfrac{3}{2}$
$= \dfrac{3}{4}sq units$
3.
(i) The points $A\left( {{x_1},{y_1}} \right),B\left( {{x_2},{y_2}} \right)$ and $C\left( {{x_3},{y_3}} \right)$ are the vertices of $\Delta ABC$. The median from $A$ meets $BC$ at D. find the coordinates of the point $D$.
(ii) The points $A\left( {{x_1},{y_1}} \right),B\left( {{x_2},{y_2}} \right)$ and $C\left( {{x_3},{y_3}} \right)$ are the vertices of $\Delta ABC$. Find the coordinates of the point $P$ on AD such that $AP:PD = 2:1$
(iii) The points $A\left( {{x_1},{y_1}} \right),B\left( {{x_2},{y_2}} \right)$ and $C\left( {{x_3},{y_3}} \right)$ are the vertices of $\Delta ABC$. Find the coordinates of points $Q$ and $R$ on medians $BE$ and $CF$, respectively such that $BQ:QE = 2:1$ and $CR:RF = 2:1$
(iv) The points $A\left( {{x_1},{y_1}} \right),B\left( {{x_2},{y_2}} \right)$ and $C\left( {{x_3},{y_3}} \right)$ are the vertices of $\Delta ABC.$ what are the coordinates of the centroid of the triangle $ABC?$
Ans: (i)
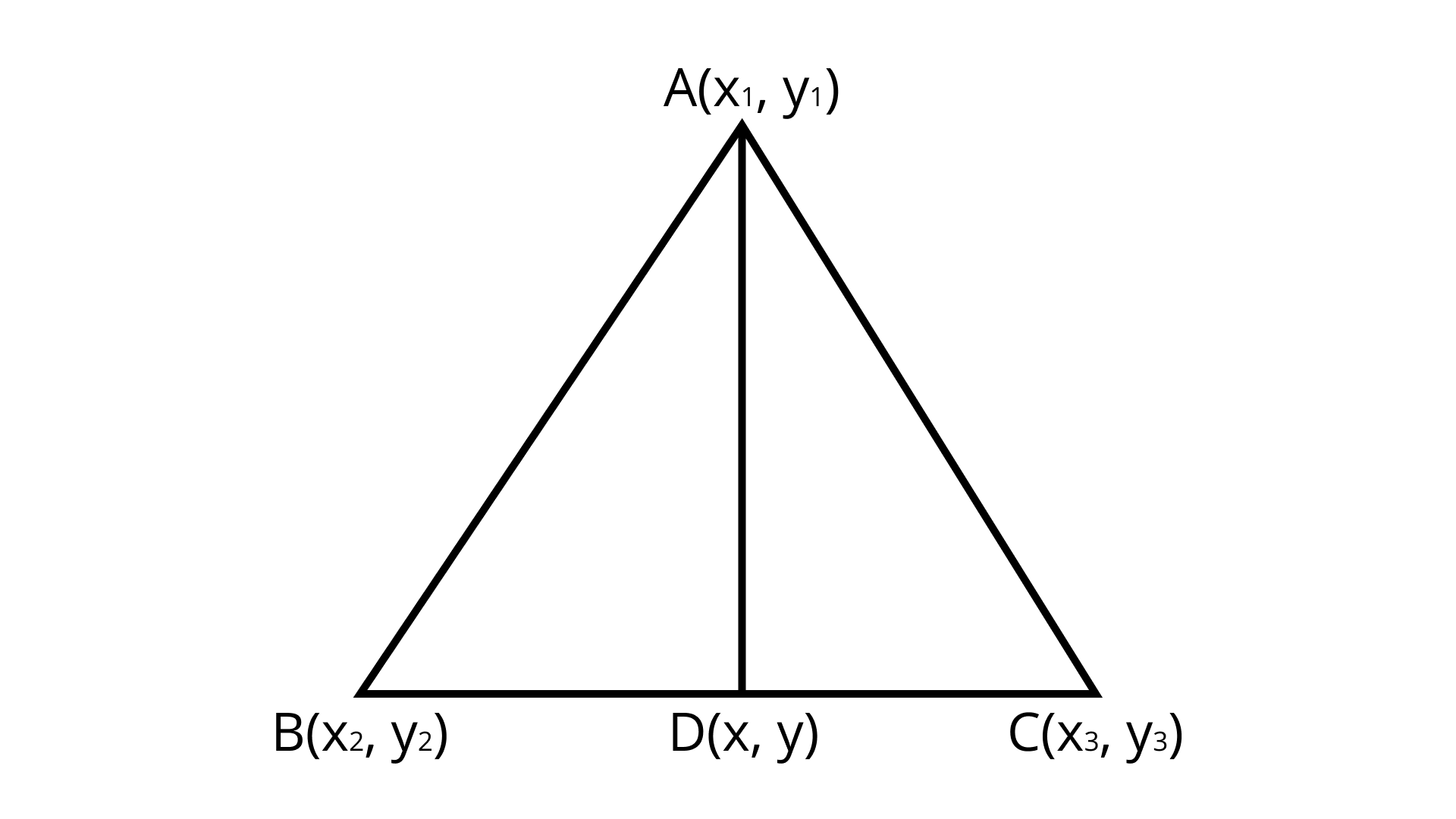
${\text{D}}$ Is the mid-point of ${\text{BC}}$
mid - point formula $= \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$
Coordinates of $D(x,y) = \left( {\dfrac{{{x_2} + {x_3}}}{2},\dfrac{{{y_2} + {y_3}}}{2}} \right)$ $\left( {{\text{By midpoint formula}}} \right)$
(ii) Explanation:
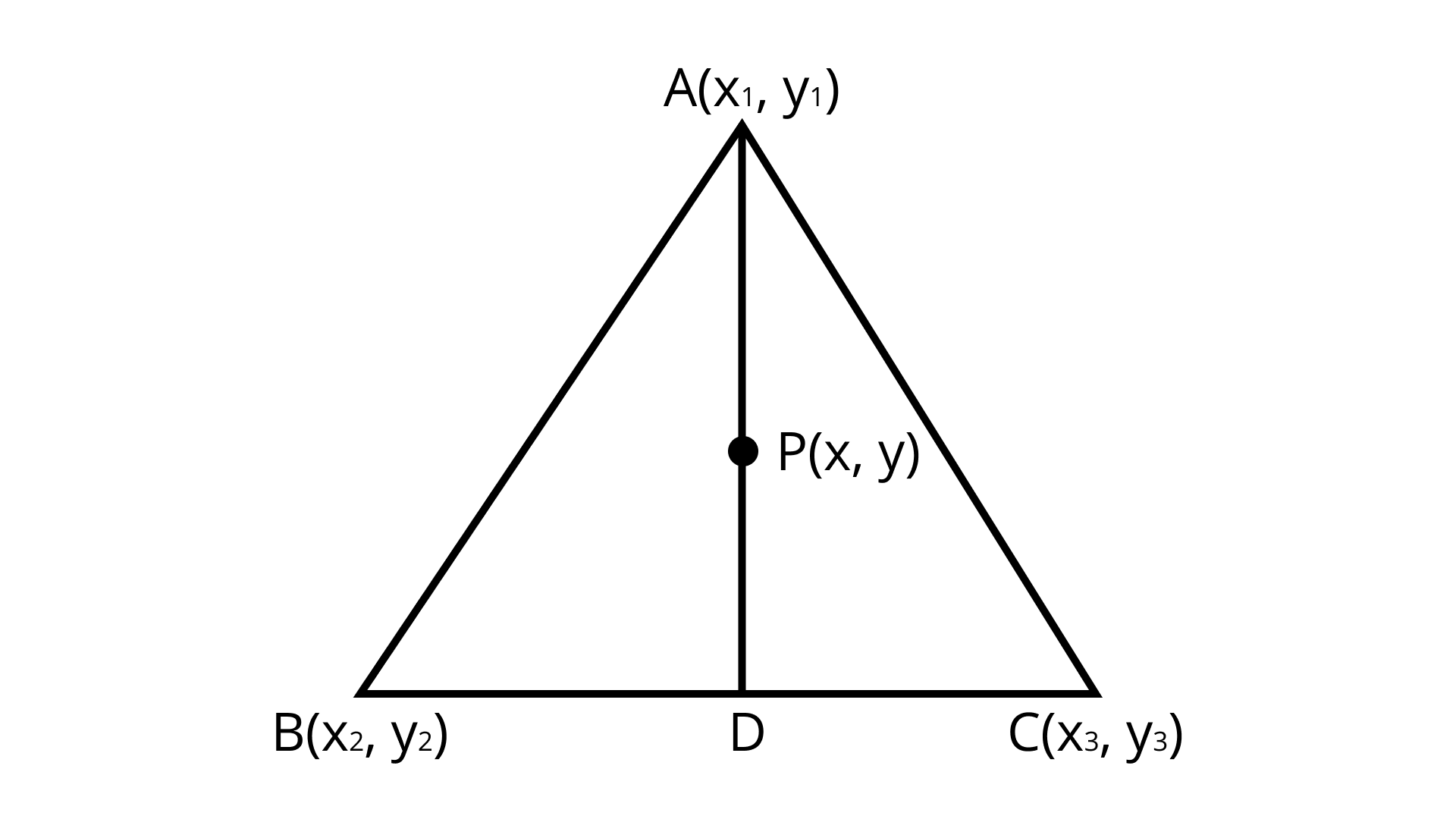
Section formula $= \left( {\dfrac{{{m_1}{x_2} + {m_2}{x_1}}}{{{m_1} + {m_2}}},\dfrac{{{m_1}{y_2} + {m_2}{y_1}}}{{{m_1} + {m_2}}}} \right)$
$D = \left( {\dfrac{{{x_2} + {x_3}}}{2},\dfrac{{{y_2} + {y_3}}}{2}} \right)$ (By Midpoint formula)
$P = \left( {\dfrac{{{m_1}{x_2} + {m_2}{x_1}}}{{{m_1} + {m_2}}},\dfrac{{{m_1}{y_2} + {m_2}{y_1}}}{{{m_1} + {m_2}}}} \right)$
$P = \left( {\dfrac{{2 \times \dfrac{{\left( {{x_2} + {x_3}} \right)}}{2} + 1 \times {x_1}}}{{2 + 1}},\dfrac{{2 \times \dfrac{{\left( {{y_2} + {y_3}} \right)}}{2} + 1 \times {x_1}}}{{2 + 1}}} \right)$
$P = \left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)$
(iii) Explanation:
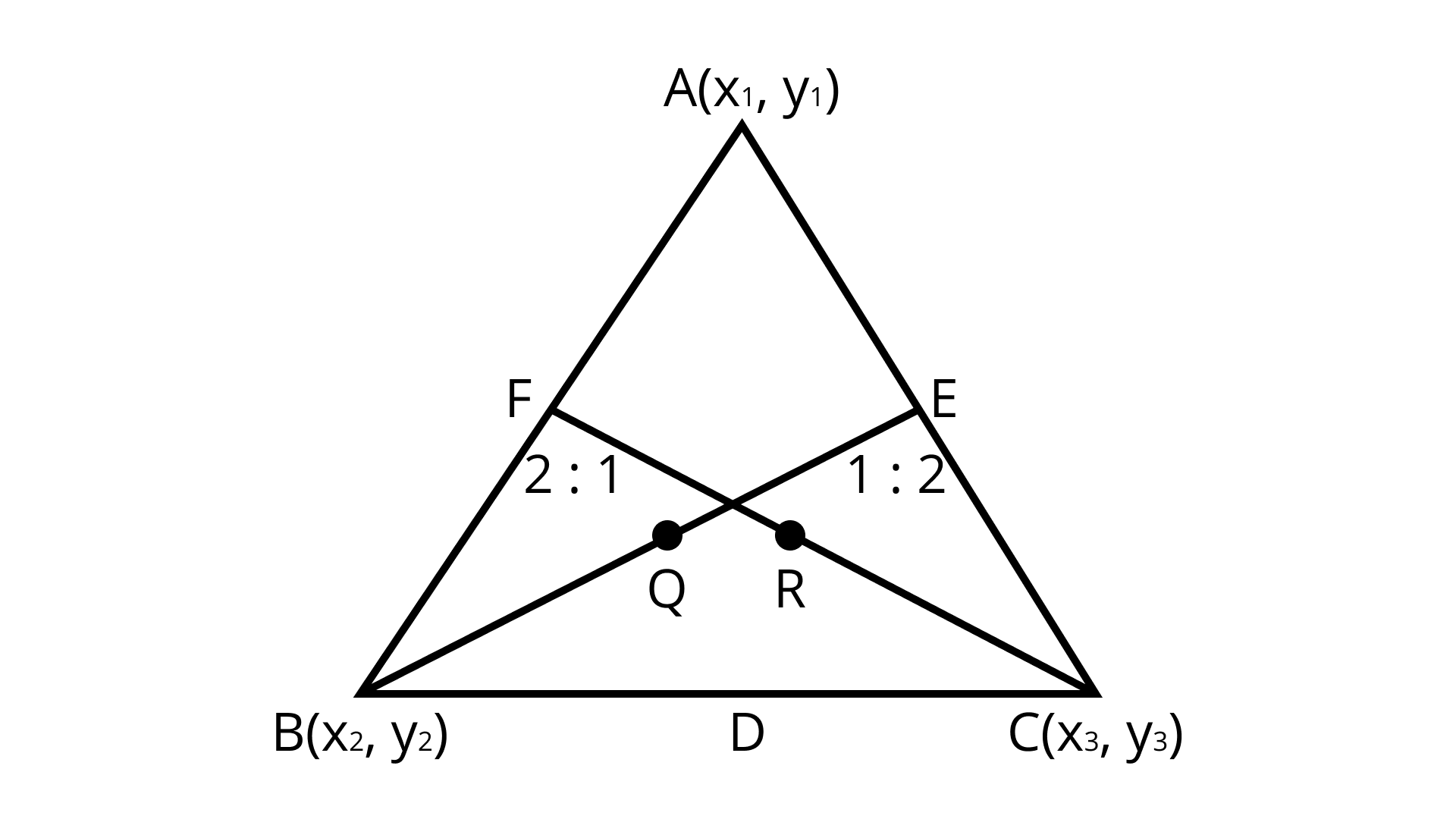
${\text{E}}$ is mid-point of ${\text{AC}}$
$E = \left( {\dfrac{{{x_1} + {x_3}}}{2},\dfrac{{{y_1} + {y_3}}}{2}} \right)$
Q divides ${\text{BF}}$ at $ 2:1$
$Q = \left( {\dfrac{{2 \times \dfrac{{\left( {{x_1} + {x_3}} \right)}}{2} + 1 \times {x_2}}}{{2 + 1}},\dfrac{{2 \times \dfrac{{\left( {{y_1} + {y_3}} \right)}}{2} + 1 \times {y_2}}}{{2 + 1}}} \right)$
$Q = \left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)$
$R$ Divides CF at $ 2:1$
$R = \left( {\dfrac{{2 \times \dfrac{{\left( {{x_1} + {x_2}} \right)}}{2} + 1 \times {x_3}}}{{2 + 1}},\dfrac{{2 \times \dfrac{{\left( {{y_1} + {y_2}} \right)}}{2} + 1 \times {y_3}}}{{2 + 1}}} \right)$
$R = \left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)$
(iv) Explanation:
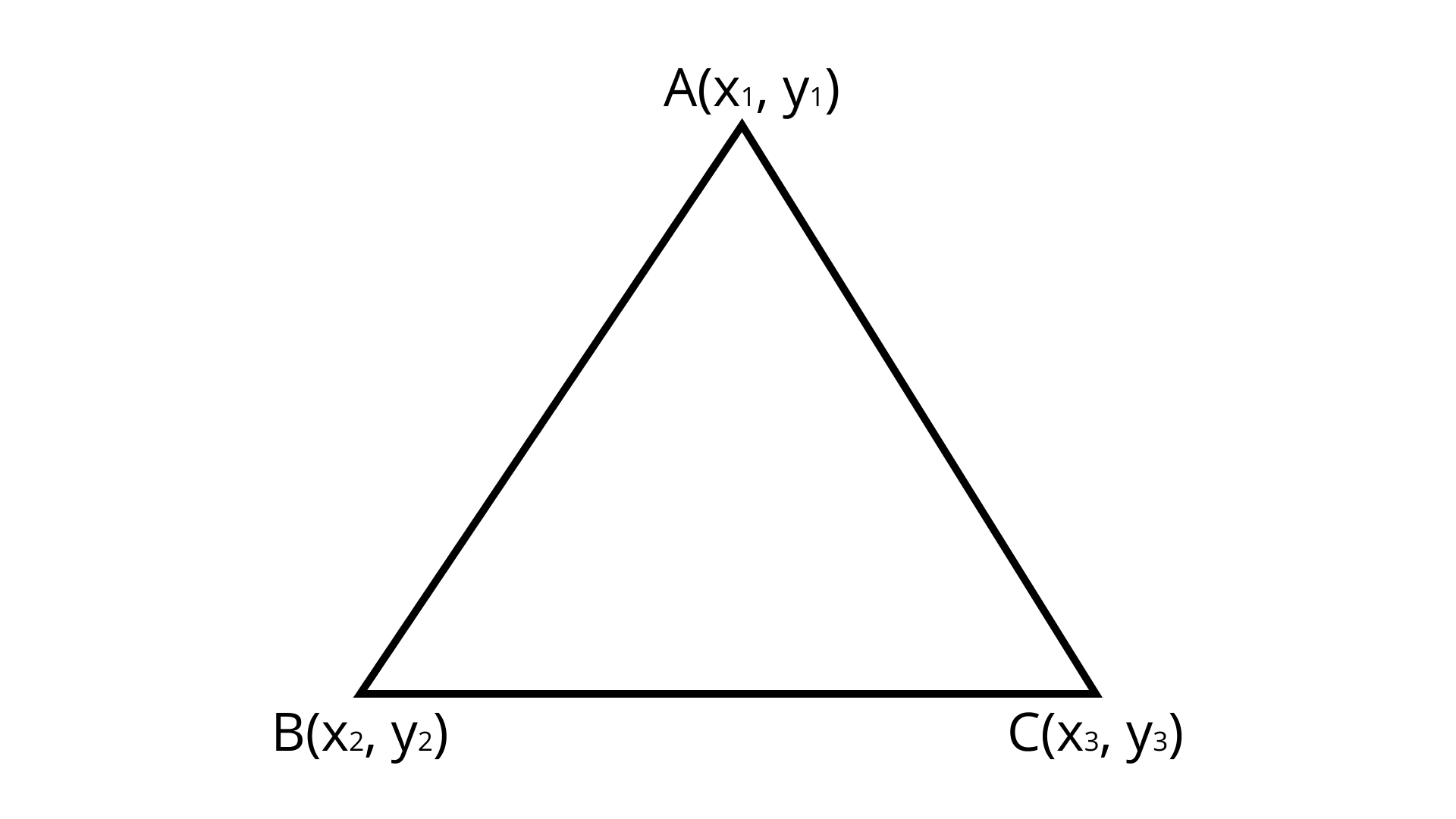
Co-ordinate of centroid
$= \left( {\dfrac{{{\text{ Sumof all coondinates of all vertices }}}}{3},\dfrac{{{\text{ Sum of all coordinates of all vertices }}}}{3}} \right)$
Centroid: The centroid is the center point of the triangle which is the intersection of the medians of a Triangle.
$\Delta {\text{ABC}}$ Coordinates of centroid $= \left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)$
4. If the points $A(1, - 2),B(2,3),C(a,2)$ and $D( - 4, - 3)$ form a parallelogram, find the value of $a$ and height of the parallelogram taking $AB$ as base.
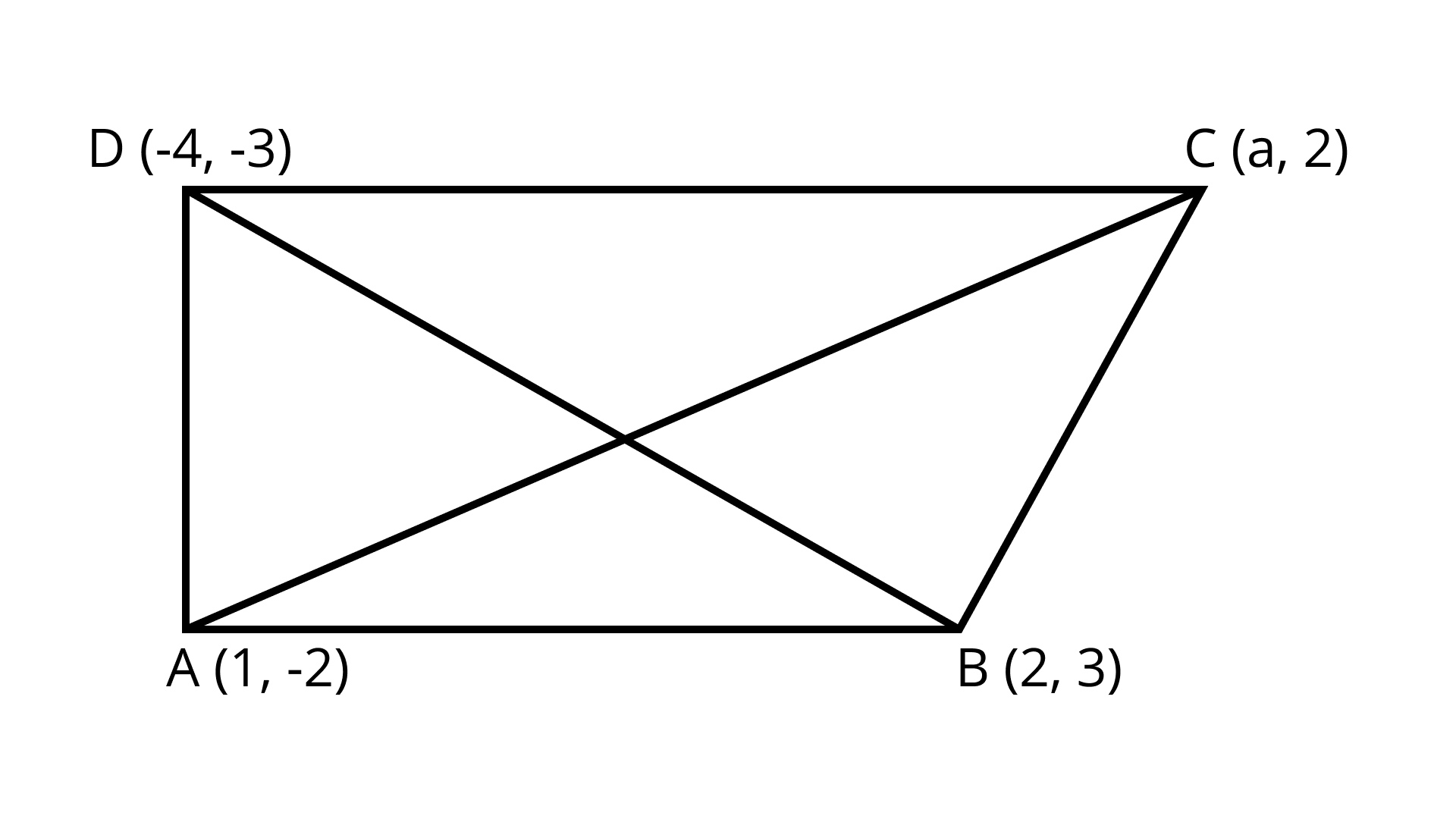
Ans: ${\text{a}} = - 3$ and height =$\dfrac{{24\sqrt {26} }}{{13}}$
We know that diagonals bisect each other
Hence, mid-point of ${\text{AC}} = $ Mid-point of BD
$\left( {\dfrac{{1 + a}}{2},\dfrac{{ - 2 + 2}}{2}} \right) = \left( {\dfrac{{2 - 4}}{2},\dfrac{{3 - 3}}{2}} \right)$
$\left( {\dfrac{{1 + a}}{2},0} \right) = ( - 1,0)$
$\dfrac{{1 + a}}{2} = - 1$
$1 + a = - 2$
$a = - 3$
$C( - 3,2)$
Area of $\Delta {\text{ABC}} = \dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right]$
$= \dfrac{1}{2}[1(3 - 2) + 2(2 + 2) + ( - 3)( - 2 - 3)]$
$= \dfrac{1}{2}[1 + 2(4) + 15]$
$= \dfrac{1}{2}\left( {24} \right) = 12{\text{ sq Units}}$
Area of parallelogram $= 2 \times $ Area of $\Delta {\text{ABC}}$
Area of parallelogram $= 2 \times 12 = 24{\text{ sq }}{\text{Units}}$
Length of $AB = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
$= \sqrt {{{(2 - 1)}^2} + {{(3 + 2)}^2}}$
$AB = \sqrt {1 + 25} = \sqrt {26}$ Units
Area of parallelogram = Base $ \times $ height
$\dfrac{{24}}{{{\text{ Base }}}} = $ Height
Height $= \dfrac{{24}}{{AB}}$
Height $= \dfrac{{24}}{{\sqrt {26} }} \times \dfrac{{\sqrt {26} }}{{\sqrt {26} }}$
$\dfrac{{24\sqrt {26} }}{{13}}$ Units
Questions 5: Students of a school are standing in rows and columns in their playground for a drill practice.${\text{A}}$ , $ {\text{B}}$ , $ {\text{C}}$ And ${\text{D}}$ are the positions of four students as shown in figure. Is it possible to place Jaspal in the Drill in such a way that he is equidistant from each of the four students ${\text{A}},{\text{B}},{\text{C}}$ and ${\text{D}}$ ? If so, what? Should be his position?
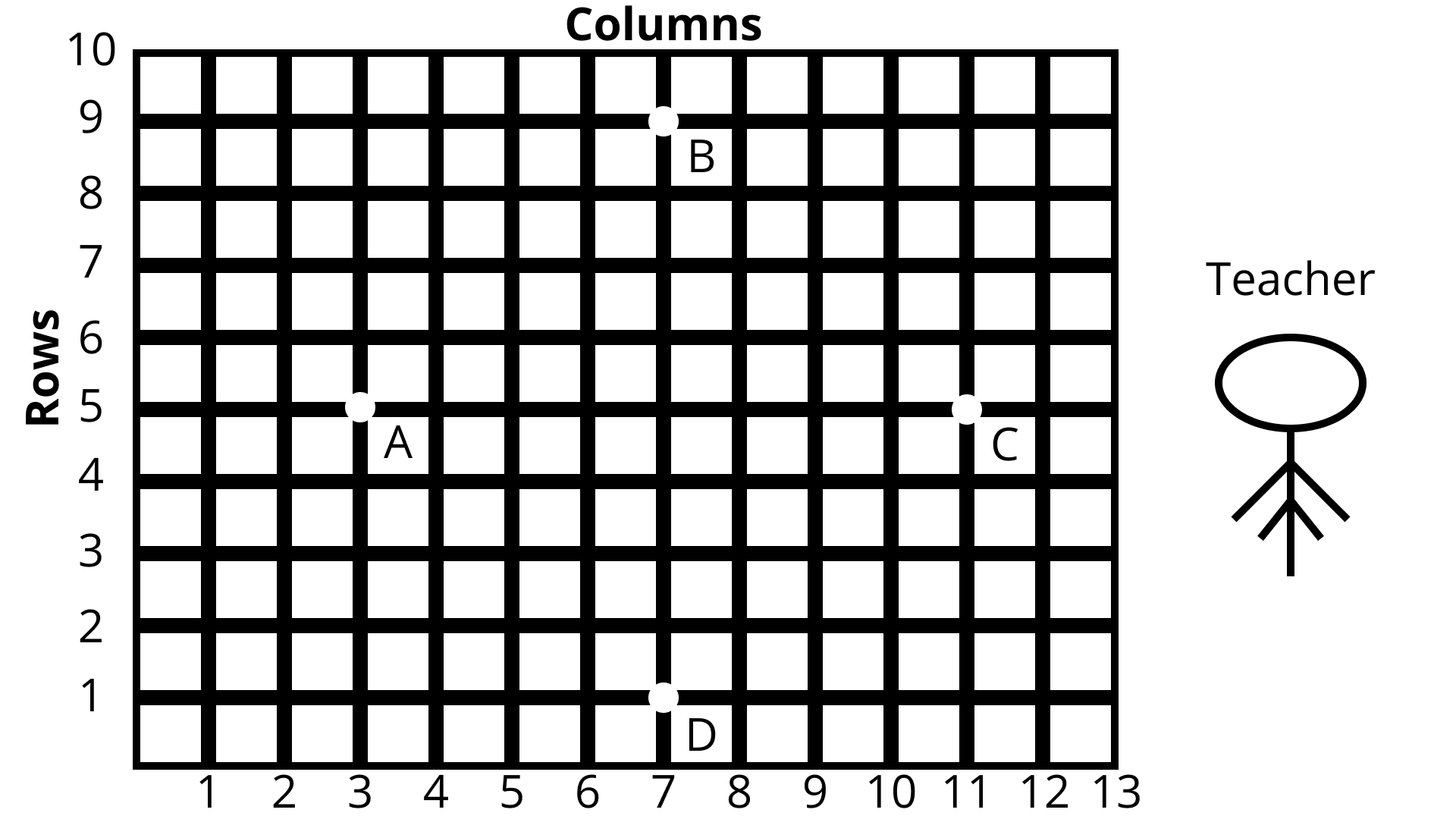
Points are ${\text{A}}(3,5),{\text{B}}(7,9),C(11,5),{\text{D}}(7,1)$
Length of ${\text{AB}} = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
${\text{AB}} = \sqrt {{{(7 - 3)}^2} + {{(9 - 5)}^2}}$
${\text{AB}} = \sqrt {16 + 16}$
$= \sqrt {32} = 4\sqrt 2$
Length of ${\text{BC}} = \sqrt {{{(11 - 7)}^2} + {{(5 - 9)}^2}}$
${\text{BC}} = \sqrt {16 + 16}$
$= \sqrt {32}$
$= 4\sqrt 2$
Length of ${\text{CD}} = \sqrt {{{(7 - 11)}^2} + {{(1 - 5)}^2}}$
${\text{CD}} = \sqrt {16 + 16}$
$= \sqrt {32}$
$= 4\sqrt 2$
Length of ${\text{AD}} = \sqrt {{{(3 - 7)}^2} + {{(5 - 1)}^2}}$
${\text{AD}} = \sqrt {16 + 16}$
$= \sqrt {32}$
$= 4\sqrt 2$
Length of ${\text{AC}} = \sqrt {{{(11 - 3)}^2} + {{(5 - 5)}^2}}$
$AC = \sqrt {(8)}$
$= 8$
Length of ${\text{BD}} = \sqrt {{{(7 - 7)}^2} + {{(1 - 9)}^2}}$
${\text{BD}} = \sqrt {64}$
$= 8$
${\text{AB}} = {\text{BC}} = {\text{AD}},{\text{AC}} = {\text{BD}}$
Hence, ABCD is square
The diagonals cut each other at mid-point, which is the equidistance from all four corners of square.
Mid – point of ${\text{AC}} = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$
$\left( {{x_1},{y_1}} \right) = (3,5)$
$\left( {{x_2},{y_2}} \right) = (11,5)$
${\text{AC}} = \left( {\dfrac{{3 + 11}}{2},\dfrac{{5 + 5}}{2}} \right)$
${\text{AC}} = (7,5)$
This should be the position of Jaspal.
6 .Ayush starts walking from his house to the office. Instead of going to the office directly, he goes to a bank first, from there to his daughter’s school and then reaches the office. What is the extra distance travelled by Ayush in reaching his office? (Assume that all distances covered are in straight lines). If the house is situated at $(2,4)$ , bank at $(5,8)$ , school at $(13,14)$ and office at $\left( {13,{\text{ }}26} \right)$ and coordinates are in ${\text{km}}$.
Ans: The given point are $(2,4),(5,8),(13,14),(13,26)$
Distance between house and bank
$= \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
$= \sqrt {{{(5 - 2)}^2} + {{(8 - 4)}^2}}$
$= \sqrt {9 + 16} = 5{\text{ Km}}$
Distance between bank and school
$= \sqrt {{{(13 - 5)}^2} + {{(14 - 8)}^2}}$
$= \sqrt {64 + 36}$
$= \sqrt {100} = 10{\text{ Km}}$
Distance between school and office
$= \sqrt {{{(13 - 13)}^2} + {{(26 - 14)}^2}}$
$= \sqrt {{{(12)}^2}} = 12{\text{ Km}}$
Distance between office and house
$= \sqrt {{{(13 - 2)}^2} + {{(26 - 14)}^2}}$
$= \sqrt {121 + 484}$
$= \sqrt {605}$
$= 24 \cdot 59{\text{ Km}}$
Total distance covered from house to bank, bank to school, school to office $= 5 + 10 + 12 = 27$
Extra distance covered$= 27 - 24.59 = 2.41{\text{km}}$
Contents of NCERT Exemplar for Class 10 Mathematics
The book contains a plethora of question papers and hence is a useful study material for the readers. This book has a total of 885 questions along with answers in 4 topics namely;
Numerical Operations
Algebra
Coordinate Geometry
Trigonometry
The book also contains detailed solutions to all the questions along with detailed answers. The exam pattern of the board exam also gets covered in the book. A detailed outline along with solutions is given for each chapter so that the students can easily understand the working of the chapters.
Free Download of the NCERT Exemplar for Class 10 Mathematics
The book is quite flexible as it allows the students to download the entire book from their account for free. They can also read the book offline and can take notes from the questions and answers. The book also provides various chapter-wise revision notes which help in enhancing the learning of the students and also in building a strong foundation of the book. Furthermore, this book contains comprehensive revision notes and chapter-wise notes in all the subjects. It also contains questions to solve the problems.
Coordinate Geometry in NCERT Exemplar for Class 10 Mathematics
Coordinate Geometry is an important chapter in NCERT Exemplar for Class 10 Maths for students of 10th Class. Coordinate Geometry is a vital portion of basic geometry. The chapter is a complete and detailed treatment of the subject. Coordinate Geometry in NCERT is one of the most important concepts taught at the secondary level. Coordinate Geometry and also coordinate geometry courses with various concepts are discussed in this chapter.
Coordinate Geometry
Coordinate Geometry is a section of Algebra, and it includes linear geometry. This chapter discusses all the points that a student should learn and understand before they enter the world of trigonometry. If students enter the world of trigonometry without understanding basic geometry, the calculations may seem difficult to them.
Questions and Solutions in the NCERT Exemplar for Class 10 Mathematics
The book also includes the problems that students will face after a brief overview of the subject. The solutions to all of these problems are provided in this chapter. The chapter includes not only questions but also the solutions to these questions.
The most important part of this chapter is coordinate geometry. Coordinate geometry is an important chapter in NCERT Exemplar for Class 10 Maths.
Topics covered in the Chapter
Coordinate Plane
It is the most important part of coordinate geometry. In this chapter, you will learn to construct coordinate planes and understand the concepts of parallel and perpendicular lines. We will also understand the concept of distance and find the distance between two points. You will also understand the definitions of coordinate axes.
Points and Lines
It is the next important topic of the chapter. In this section, you will learn about points and lines. We will learn to understand the concept of the point-line system and its properties. You will also learn the fundamental idea of a line that will be used to understand coordinate geometry.
Angles and Triangles
In this section, we will learn the concept of angle and triangle. You will learn to understand the concepts of the law of sines and cosines.
Trigonometry
It is a part of coordinate geometry. In this chapter, you will learn to understand the concept of ratio and degree. You will learn to understand the concept of the unit circle and different types of radii. You will also learn the conversion between degrees and radians. You will learn to use basic trigonometry formulas to solve algebraic equations.
Graphing with Graphs
It is a very important chapter in coordinate geometry. In this chapter, we will learn to construct the graphing of coordinates of points and find the points for any given line. We will also learn to draw the graphs of various coordinate systems. Graphs are very helpful in giving an accurate view of the given topic. They help us to visualize and understand it intuitively. The problem of graphing can be solved by using graphs. They help us to understand the underlying concepts easily.
Free PDF download of NCERT Exemplar for Class 10 Mathematics
Free PDF download of NCERT Exemplar for Class 10 Maths Chapter 7 - Coordinate Geometry solved by expert Maths teachers on Vedantu.com as per NCERT (CBSE) Book guidelines. All Chapter 7 - Coordinate Geometry exercise questions with solutions to help you to revise the complete syllabus and score more marks in your examinations. Vedantu is a platform that provides free NCERT Solutions and other study materials for students. You can download NCERT Solutions Class 10 Maths to help you to revise the complete Syllabus and score more marks in your examinations. Subjects like Science, Maths, English will become easy to study if you have access to NCERT Solution Class 10 Science, Maths solutions, and solutions of other subjects that are available on Vedantu only.
FAQs on NCERT Exemplar for Class 10 Maths Chapter 7 - Coordinate Geometry (Book Solutions)
1. How should I tackle questions of the form "Which line is parallel to line BAB and intersects line ABC at point D?"
As a general rule, if several lines have the same gradient then any line on that line will intersect the desired line. For example, let us consider the line:
AB = DC (1)
Let us take the line CBA, which intersects AB at point D. If C is taken to be the line parallel to AB and having the same gradient, then line CBA intersects line AB at point D.Another example would be if you wanted to find a line which intersects a line at a particular angle.
2. Can I Download NCERT Maths Exemplar for my Class?
To download NCERT Maths Exemplar Question Paper, just click on the download button and fill up the required information. After the download, you will get a .doc or .pdf format file of the NCERT maths question paper. The entire NCERT Exemplar is free to download from Vedantu’s website or app and use example question paper for Class 10 Maths. The PDF file can be opened in Adobe Reader and MS Word. You can save the PDF file as a print-ready file and share it with your friends. We recommend that you print it and keep it with your notes and books. You can study from the NCERT Exemplar question paper for better understanding and preparation.
3. What is the Main Objective of the Subject?
It helps students to know more about the basics of the concept of Geometry. It also helps students to develop their logic, judgment, and creativity. Moreover, it prepares students for other branches of science and to understand the basics of Mathematics. The main topics covered in the subject are-
Fundamentals of Geometry, Projective Geometry, Descriptive Geometry, Coordinate Geometry, Spatial Relations, Functions, Vector Calculus, Coordinates and Curves, Maths Review (Maths for Class 10), Algebra, Pre-Algebra, Geometric Algebra, Vector, Tensor, Matrix and General Calculus, Differential Geometry, Topology.
4. What Aspects of Mathematics should be Covered?
Every subject has different aspects which are to be covered. Mathematics, which is one of the most difficult subjects, has various aspects to be covered. Students should be taught a particular aspect of mathematics to cover all the aspects of that subject. For example, they should be taught how to write mathematical symbols; they should be taught how to read and interpret mathematical symbols; they should be taught how to apply mathematics; they should be taught how to understand mathematical concepts; they should be taught how to apply mathematics; they should be taught how to study
mathematics; etc.
5. What is a Study Guide?
NCERT Study Guides are carefully prepared books with chapters and subchapters, that enable a student to read a text and gain a deep understanding of the topics taught. Often the best feature of NCERT Study Guides is that they are accessible and interesting. These study guides are then studied carefully by our experts at www.vedantu.com. They now prepare notes for the children and the teachers to refer from. We possess a massive section for resources where you can find almost anything.









































