Question

Use graph paper for the question (Take 2cm=1 unit along both x and y axis). ABCD is a quadrilateral whose vertices are A (2, 2), B (2, -2), C (0, -1) and D ( 0, 1). Reflect quadrilateral ABCD on the y-axis and name it as A’B’CD.

Answer 1

Hint: Roughly draw the coordinates of the quadrilateral. Reflected quadrilateral will be a mirror like which will be formed on the left side of the Cartesian plane. A and B coordinates will have reflections A’ and B’ while C and D coordinates won’t have any change.

Complete step-by-step answer:
The quadrilateral ABCD is a trapezium, which can be obtained by drawing ABCD in the graph.
We have been given the coordinates of quadrilateral ABCD as A (2, 2), B (2, -2), C (0, -1) and D (0, 1). All these coordinates lie in the x-y plane i.e. they lie in the first quadrant and fourth quadrant of the Cartesian plane.

What we have to do is to reflect these points onto the second and third quadrant of the Cartesian plane.

 Let us draw a rough figure to understand how the reflection of coordinates takes place.

Here point A (2, 2) reflected gives point A’ (-2, 2) on 2nd quadrant. Similarly, point B (2, -2) reflected on the 3rd quadrant gives B’ (-2, -2).

In the 1st quadrant both x and y values of the coordinates (x, y) are positive.

In 2nd quadrant x is negative and y is positive i.e. (-x, y).

In 3rd quadrant both x and y are negative i.e. (-x, -y).

And in the final quadrant x is positive and y negative i.e. (x, -y).

So A in the 1st quadrant is reflected to A’ in the 2nd quadrant and B in the 4th quadrant is reflected to B’ in the 3rd quadrant.

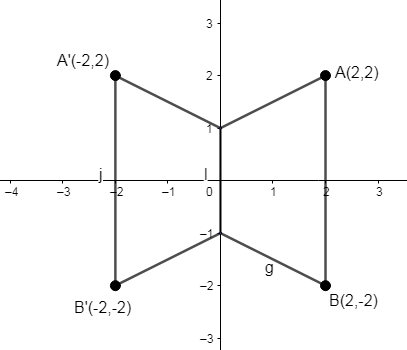
From the figure ABCD represents the original quadrilateral and A’B’CD represents the reflected quadrilateral. Coordinates C(0, -1) and D(0, 1) are common points to both the quadrilaterals.

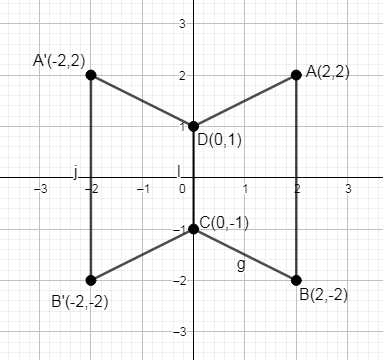
Therefore the above graphical representation shows quadrilateral ABCD and its reflected quadrilateral A’B’CD.

Note: In a question like this, first try to draw a rough figure, using the given coordinates if you can’t understand the question. We know how mirror images are formed. Just reflect and draw it on the other side of the y-axis and find the coordinates forming the reflected quadrilateral A’B’CD.