Question

There are 504 cones each of diameter 3.5cm and height 3 cm are melted and recast into a metallic sphere. Find the diameter of the sphere. Use $\pi = \dfrac{{22}}{7}$.

Answer 1

Hint:In order to solve this problem you need to find the volume of 504 cones then with the help of that volume find the radius of the sphere formed and then calculate its diameter. Doing this will give you the right answer.

Complete step-by-step answer:

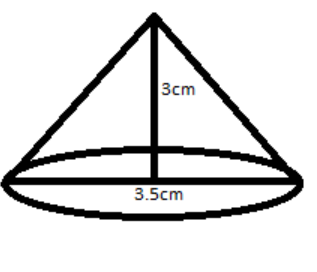
There are 504 cones each of radius 3.5cm and height 3cm.
We know the formula for volume of cone is $\dfrac{1}{3}\pi {r^2}h\,\,\,\,\,\,\,\,r = 3.5,\,\pi = \dfrac{{22}}{7}\,\,{\text{and }}\,h = 3$
So the volume of 504 cones is =$504 \times \dfrac{1}{3} \times \dfrac{{22}}{7} \times {(3.5)^2}(3) = 19404c{m^3}$
When all the cone is melted the new sphere is formed the volume of the sphere will be equal to the volume of 504 cones.
We know the volume of the sphere of radius R can be $\dfrac{4}{3}\pi {R^3}$
So we do, $\dfrac{4}{3}\pi {R^3}$=19404
$
  {R^3} = \dfrac{{19404 \times 3 \times 7}}{{22 \times 4}} = 4630.5 \\
  {R^3} = 4630.5 \\
  R = 16.66cm \\
$
So, the radius of the sphere is 16.66 centimeter.

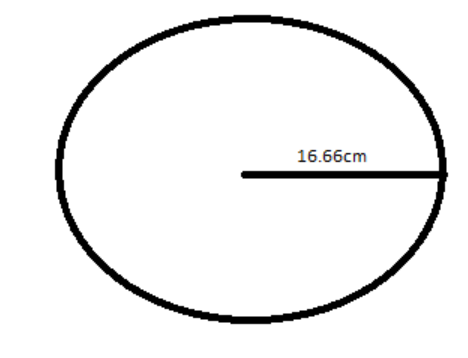
Then the diameter will be d = 2R = 16.66(2)=33.32 centimeters
The diameter of the sphere obtained by melting those 504 cones in 33.32 centimeters.

Note:Whenever you face such types of problems then obtain something from the given data then apply it to find the asked term. Here we have calculated the volume of all the cones then we have equated the formula of volume of sphere and the volume of all the cones since cones are melted to form a sphere then the quantity which will be the same is the volume then we have calculated the radius and then diameter. Proceeding in this way your problem will be solved and you will get the right answer.