Question

The Wharton’s jelly in umbilical cord is:
A. Mucoid connective tissue
B. Reticular connective tissue
C. Areolar connective tissue
D. Adipose connective tissue

Answer 1

Hint: The Wharton’s jelly is largely made up of mucopolysaccharides. It is a gelatinous compound found in the umbilical cord and named after the scientist T. Wharton.

Complete answer: Wharton’s jelly is a gelatinous or jelly-like material in the umbilical cord. It is also known as ‘substantia gelatinosa funiculi umbilicalis’. It is made up of muco-polysaccharides. It contains chondroitin sulphate and hyaluronic acids.
The jelly is so named because the English anatomist Thomas Wharton had first described it in his publication ‘Adenographia’.
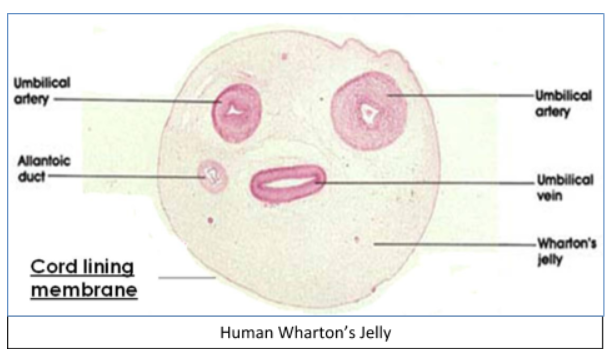
It is a type of mucoid connective tissue and surrounds arteries and vein of the umbilical cord. Wharton’s jelly is derived from extraembryonic mesoderm.
It contains some cells such as fibroblasts and macrophages.
The cells present there express telomerase genes and other stem cell genes as well. It is a source of adult stem cells and can be collected from umbilical cord blood for experiments of stem-cell therapy.

So, the correct option is A. Mucoid connective tissue.

Additional information: Reticular connective tissue is mesh-like connective tissue network made up of reticular fibres, collagen etc. often found in the kidney, spleen, lymph nodes etc.
Areolar connective tissue is loose connective tissue that surrounds blood vessels, nerve bundles, some organs and muscles.
Adipose connective tissue is also a loose connective tissue that stores fat. It is made up of adipocytes. It helps in insulation of our body.

Note: Mucoid connective tissue is also called mucous connective tissue in some articles/books.
Human Wharton’s jelly can be of the following types:
Perivascular Wharton’s jelly,
Intravascular Wharton’s jelly and
Subamniotic Wharton’s jelly.