Question

The volume of frustum of cone \[{\text{1600m}}{{\text{m}}^{\text{3}}}\], the base and the upper area of the circle is \[{\text{16m}}{{\text{m}}^2}\]and \[{\text{100m}}{{\text{m}}^2}\]. Find the height of the cone.
A. \[{\text{30}}{\text{.76mm}}\]
B. \[{\text{11}}{\text{.25mm}}\]
C. \[{\text{12}}{\text{.25mm}}\]
D. \[{\text{13}}{\text{.25mm}}\]

Answer 1

Hint: As we know that the area of circle is given as \[{\text{$\pi$ }}{{\text{r}}^{\text{2}}}\]. From this calculate the radius of both base and upper circle. And then apply the formula of volume of frustum which is \[{\text{v = }}\dfrac{{{\text{$\pi$ h}}}}{{\text{3}}}{\text{(}}{{\text{R}}^{\text{2}}}{\text{ + Rr + }}{{\text{r}}^{\text{2}}}{\text{)}}\]. And thus from all these we can easily calculate the height of the frustum of cone.

Complete step by step answer:

Diagram:
 

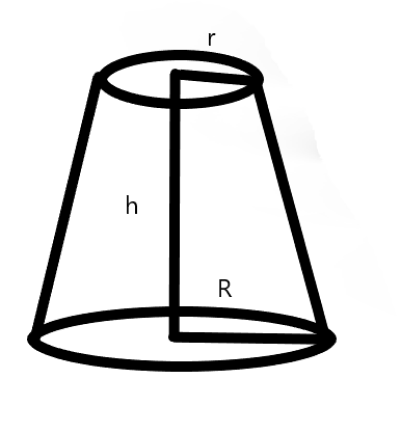
Let R and r be the radius of upper and base circle. As the base and the upper area of the circle is \[{\text{16m}}{{\text{m}}^2}\]and \[{\text{100m}}{{\text{m}}^2}\].
\[
  {\text{for ,A = $\pi$ }}{{\text{R}}^{\text{2}}}{\text{ = 100}} \\
   \Rightarrow {{\text{R}}^{\text{2}}}{\text{ = }}\dfrac{{{\text{100}}}}{{\text{$\pi$ }}} \\
  {\text{On taking root we get,}} \\
   \Rightarrow {\text{R = }}\dfrac{{{\text{10}}}}{{\sqrt {\text{$\pi$ }} }} \\
  {\text{for,A = $\pi$ }}{{\text{r}}^{\text{2}}}{\text{ = 16}} \\
   \Rightarrow {{\text{r}}^{\text{2}}}{\text{ = }}\dfrac{{{\text{16}}}}{{\text{$\pi$ }}} \\
  {\text{On taking root we get,}} \\
   \Rightarrow {\text{r = }}\dfrac{{\text{4}}}{{\sqrt {\text{$\pi$ }} }} \\
 \]
Now, put the value of volume given and both the radii in the formula of volume of frustum, we get
\[{\text{v = }}\dfrac{{{\text{$\pi$ h}}}}{{\text{3}}}{\text{(}}{{\text{R}}^{\text{2}}}{\text{ + Rr + }}{{\text{r}}^{\text{2}}}{\text{)}}\]
 \[
   \Rightarrow {\text{v = }}\dfrac{{{\text{$\pi$ h}}}}{{\text{3}}}{\text{(}}\dfrac{{{\text{100}}}}{{\text{$\pi$ }}}{\text{ + (}}\dfrac{{{\text{10}}}}{{\sqrt {\text{$\pi$ }} }}{\text{)(}}\dfrac{{\text{4}}}{{\sqrt {\text{$\pi$ }} }}{\text{) + }}\dfrac{{{\text{16}}}}{{\text{$\pi$ }}}{\text{)}} \\
   \Rightarrow {\text{1600 = }}\dfrac{{{\text{$\pi$ h}}}}{{\text{3}}}{\text{(}}\dfrac{{{\text{156}}}}{{\text{$\pi$ }}}{\text{)}} \\
   \Rightarrow {\text{52h = 1600}} \\
   \Rightarrow {\text{h = }}\dfrac{{{\text{1600}}}}{{{\text{52}}}} \\
   \Rightarrow {\text{h = 30}}{\text{.76mm}} \\
 \]
Hence, option (a) is our correct answer.

Note: In geometry, a frustum is a portion of a solid (normally a cone ) that lies between one or two parallel planes cutting it. A right frustum is a parallel truncation of a right pyramid or right cone.
The formula to calculate the volume of the frustum is basically the volume of the big cone minus the volume of the small cone which is cut off.
The formula of volume of frustum which is \[{\text{v = }}\dfrac{{{\text{$\pi$ h}}}}{{\text{3}}}{\text{(}}{{\text{R}}^{\text{2}}}{\text{ + Rr + }}{{\text{r}}^{\text{2}}}{\text{)}}\].