Question

The reflection of the line \[x = 1\] in the line \[{\text{x + y = 1}}\] is
\[
  A.x = 0 \\
  B.x{\text{ }} + {\text{ }}y{\text{ }} = - 1 \\
  C.x{\text{ }} - {\text{ }}y{\text{ }} = - 1 \\
  D.y{\text{ }} = {\text{ }}0 \\
 \]

Answer 1

Hint: We are provided with an equation of 2 lines. We can obtain the reflected line by putting the value of the equation the line to be reflected in the equation of the line to be reflected on i.e. here we put the value of x=1 in the equation of other line \[{\text{x + y = 1}}\].

Complete step-by-step answer:
First of all we can draw a graph to get a better understanding of the question. Here the line \[{\text{x + y = 1}}\] acts as a mirror and makes reflection of the line ${\text{x = 1}}$.

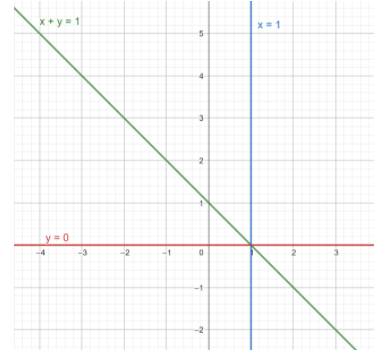
Let ,
\[{\text{x + y = 1}}\]
\[{\text{x = 1}}\].
We need to find out the equation of the reflected line.
We get,
${\text{1 + y = 1}}$
Subtracting 1 from both sides, we get
${\text{y = 0}}$
Therefore, the equation of the reflected line is y = 0
So, the correct answer is option D

Note: The solution can also be found out graphically. This can be obtained by taking the angle of incidence and angle of reflection. For reflections on a line or a plane mirror, the angle of incidence and angle of reflection are equal. For geometrical problems, it is recommended to draw the figure. If the question is to find the reflected image of a point, we can obtain the x and y coordinates by giving the given coordinates in the equation of the line. In case the line is either of the axes, x is taken as -x for y axis is the line of reflection and y is taken as -y when x axis is the line.