Question

The length of a rectangular blackboard is 8cm more than its breadth. If its length is increased by 7 cm and the breadth is decreased by 4cm, its area remains unchanged. Find the length and the breadth of the rectangular blackboard.

Answer 1

Hint: In this question let the length and the breadth of the rectangular blackboard be variables, use the constraint given in the question to formulate equations, then solve to get the value of the variables. Use the area of the rectangle as a product of length and breadth.

Complete step-by-step answer:

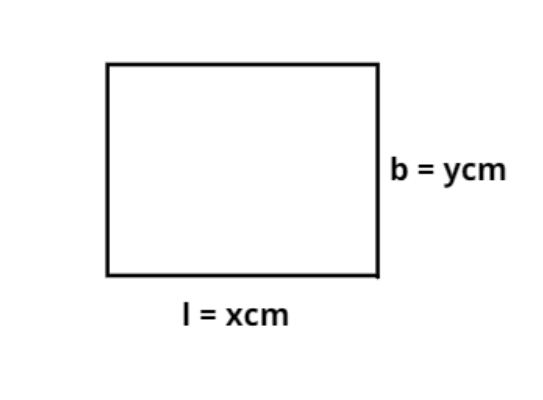
Let the length (l) of rectangular blackboard be x cm.
And the breadth (b) of the rectangular blackboard be y cm.
Now as we know that the area (A) of the rectangle is the multiplication of length (l) and breadth (b).
$ \Rightarrow A = l.b{\text{ c}}{{\text{m}}^2}$............................. (1)
Now it is given that the length of the rectangular blackboard is 8 cm more than its breadth.
$ \Rightarrow x = 8 + y$............................ (2)
Now from equation (1) the area (A1) of the rectangle is
$ \Rightarrow {A_1} = \left( {8 + y} \right)y{\text{ c}}{{\text{m}}^2}$............................... (3)
Now it is also given that if length is increased by 7 cm and breadth is decreased by 4 cm its area remains the same.
Originally the length of blackboard is (8 + y) now length is increased by 7 cm therefore new length of the rectangle blackboard is (y + 8 + 7) = (y + 15).
Now originally the breadth of the blackboard is (y) now breadth is decreased by 4 cm therefore new breadth of the rectangle blackboard is (y – 4).
So from equation (1) the area (A2) of the new rectangle is
$ \Rightarrow {A_2} = \left( {15 + y} \right)\left( {y - 4} \right){\text{ c}}{{\text{m}}^2}$................................... (4)
Now it is given that both the areas are equal.
So equate equation (3) and (4) we have,
$ \Rightarrow \left( {8 + y} \right)y = \left( {15 + y} \right)\left( {y - 4} \right)$
Now simplify the above equation we have,
$ \Rightarrow 8y + {y^2} = 15y - 60 + {y^2} - 4y$
$ \Rightarrow 3y = 60$
Now divide by 3 we have,
$ \Rightarrow y = 20$ cm.
Now from equation (2) we have,
$ \Rightarrow x = 8 + y = 8 + 20 = 28$ cm.
So the length and breadth of the rectangular blackboard is 28 and 20 cm respectively.
Hence option (A) is correct.

Note: A rectangle is a 2D shape with 4 sides and 4 corners. The two sides meet at an angle of ${90^0}$, moreover the opposite sides of the rectangle are equal in length and are parallel to each other, since the given blackboard is of rectangle shape, thus it must possess all these properties. It is advised to remember the direct basic formula for area for shapes like rectangle, circle, square etc. as it helps saving a lot of time.