Question

The inner diameter of a circular building is 54 cm and the base of the wall occupies a space of 2464 \[c{{m}^{2}}\]. The thickness of the wall is
A. 1 cm
B. 2 cm
C. 4 cm
D. 5 cm

Answer 1

Hint: Inner diameter of circular building under consideration is given. In order to find, thickness of the wall. We need to find out the first outer radius of the circular building. To find the outer radius, the Area base of the wall is given in question, using this area we can find the outer radius. Then, the thickness of the wall would be outer radius minus inner radius.
Complete step by step solution:
The top view is shown below

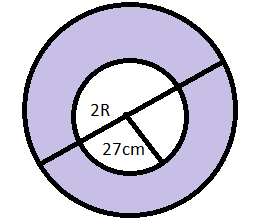
Inner diameter of circular building is 54 cm
So, inner radius of circular building would be 27 cm
Let, outer radius of the wall be R cm. Because the base of the wall is circular in shape with R as its radius.
So, according to question:
\[\begin{align}
  & \pi {{R}^{2}}=2464c{{m}^{2}} \\
 & \Rightarrow {{R}^{2}}=\dfrac{2464}{\pi } \\
 & \Rightarrow {{R}^{2}}=\dfrac{2464}{22}\times 7 \\
\end{align}\]
Now, we can express 2464 as factors to cancel off similar terms as shown below,
\[\begin{align}
  & \Rightarrow {{R}^{2}}=\dfrac{22\times 28\times 4\times 7}{22} \\
 & \Rightarrow R=28cm \\
\end{align}\]
Hence, the outer radius of the circular building is 28 cm. We have found the inner radius of this circular building i.e. 27 cm.
Therefore, the thickness of this circular building would be equal to the difference between outer radius & inner radius.
The thickness of wall = (Outer radius) – (Inner radius)
= 28 – 27 = 1 cm.
Hence, the thickness of the wall is 1 cm.
Note: Don’t confuse equating the equation above like (Outer area) – (inner area) = 2464. This isn’t what the question is saying. Question is clearly saying to compute it with the equation (Outer area) = 2464. If the question would be like the difference between outer area and inner area is 2464. Then, we would be using (Outer area) – (inner area) = 2464.