Question

Let ABCD be a trapezium with parallel sides AB, CD such that the circle S with AB as its diameter touches CD. Further, the circle S passes through the midpoints of the diagonals AC and BD of the trapezium. The smallest angle of the trapezium is
a. $ \dfrac{\pi }{3} $
b. $ \dfrac{\pi }{4} $
c. $ \dfrac{\pi }{5} $
d. $ \dfrac{\pi }{6} $

Answer 1

Hint: We will first prove that ABCD is an isosceles trapezium. Then, we will use the concept that the corresponding interior angle between two parallel lines is equal to 180˚ to find the \[\angle ABC\] and \[\angle BCD\] . Then we will choose the angle which measures the smallest among \[\angle ABC\] and \[\angle BCD\].

Complete step-by-step answer:
It is given in the question that ABCD be a trapezium with parallel sides AB, CD such that the circle S with AB as its diameter touches CD. Further, the circle S passes through the midpoints of the diagonals AC and BD of the trapezium. And we have been asked to find the smallest angle of the trapezium.
According to the given conditions, we can draw the figure as follows.

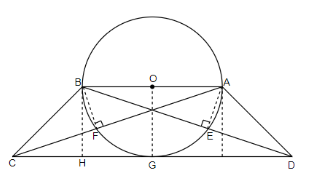
We know that AB is the diameter of the circle and the angle subtended by the circle is equal to 90˚. In triangle ABC, we get that BF is perpendicular to AC, as it is given in the question that F is the midpoint of the diagonal AC and that the circle passes through that point.
Also, we know that both triangle ABF and triangle CBF are right angled triangles in which base and height are of the same length. From this, we can say that hypotenuse CB in triangle BCF is equal to hypotenuses AB in triangle ABF. So, we get, side AB = BC. Hence, we can say that the triangle ABC is an isosceles triangle.
Similarly, we have side AD = AB so ABD is also an isosceles triangle.
As we get AB = BC and AB = AD, we can say that, AB = BC = AD, that is BC = AD. Thus, ABCD is an isosceles trapezium.
Now, we have O as the center of the circle S and OG, BH are perpendicular to CD, also AB is parallel to CD. So, we get,
 $ \angle BOG=\angle OGH=\angle GHB={{90}^{\circ }} $
This means that OBHG is a square. So, we will get OG = BH. We can also see from the figure that, OG = OB as they are the radius of the circle. So, we can write, BH = OB.
Also, BC = AB = 2OB = 2BH
So, we get, $ \dfrac{BH}{BC}=\dfrac{1}{2} $
We know that $ \sin \theta =\dfrac{perpendicular}{hypotenuse} $ . Now, if we consider triangle CBH, we can write, $ \sin \left( \angle BCH \right)=\dfrac{1}{2} $
We know that when $ \theta =\dfrac{1}{2} $ , it means that $ \theta $ is at $ \dfrac{\pi }{6} $ .
Now, we know that ABCD is an isosceles trapezium, so we get,
 $ \angle BCH=\angle ADC=\dfrac{\pi }{6} $
As we know that AB is parallel to CD and the sum of the corresponding interior angles is equal to 180˚, we get,
 $ \angle ABC+\angle BCD={{180}^{\circ }} $
We know that $ \angle BCD={{30}^{\circ }} $ , so on putting $ \angle BCD={{30}^{\circ }} $ in $ \angle ABC+\angle BCD={{180}^{\circ }} $ , we get,
 $ \angle ABC+{{30}^{\circ }}={{180}^{\circ }} $
Transposing 30˚ from LHS to RHS, we get,
 $ \begin{align}
  & \angle ABC={{180}^{\circ }}-{{30}^{\circ }} \\
 & \angle ABC={{150}^{\circ }} \\
\end{align} $
Therefore, the smallest angle of the trapezium ABCD is $ \dfrac{\pi }{6} $ .
Hence, option (d) is the correct answer.

Note: Many times, the students make mistake in understanding the term isosceles trapezium, they may think that it means that the measures of all the sides of the trapezium are equal, but this is not correct as actually, if all the four sides are equal, then it is called a square. The measure of all the angles of a square is equal to 90˚ and here we can see that the angles have different values, hence it is not a square.