In the adjoining figure, $CBA$ is secant and $CD$ is tangent to the circle. If $AB=7cm$ and
$BC=9cm$, then find the length of $CD$.
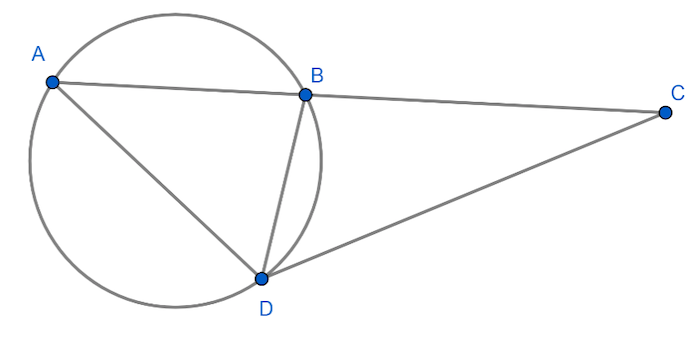
Answer
Verified361.5k+ views
Hint: We can equate the ratio of corresponding sides of similar triangles if we can prove that any two triangles that contain the sides $AC$, $BC$ and $CD$ are similar triangles. By equating this ratio, we can get a relation between these three sides.
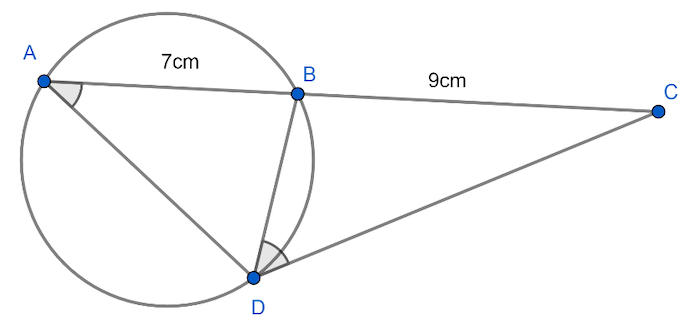
In the above figure, let us consider $\Delta ADC$and $\Delta DBC$.
From the figure, we can see that the angle $C$ is common in both triangles. So, we can write
$\angle C=\angle C........\left( i \right)$
Also, there is a property of the circle which is related to the tangent and chord. This property states that
“the angle between the chord and the tangent is equal to the angle made by the chord in the alternative
segment”. Using this property in the above figure in $\Delta ADC$and $\Delta DBC$, we get
$\angle DAC=\angle BDC.......\left( ii \right)$
From equation $\left( i \right)$ and equation $\left( ii \right)$ , using $AA$ similarity rule, we get that
the triangles are similar.
$\Delta ADC\sim \Delta DBC$
Since these two triangles are similar, we can equate the ratio of corresponding sides of the
corresponding triangles. This means that we can equate the following sides,
$\dfrac{BC}{DC}=\dfrac{DC}{AC}$
$\Rightarrow {{\left( DC \right)}^{2}}=AC\times BC........(iii)$
It is given in the question that side $BC=9cm$.
We can see from the figure that $ABC$ is a straight line. So, we can obtain a relation as below,
$AC=AB+BC........(iv)$
Substituting values of $AB=7cm$ and $BC=9cm$ in equation $(iv)$, we get
$AC=7+9$
$\Rightarrow AB=7cm$
Substituting the values of $AC=16cm$ and $BC=9cm$ in equation $\left( iii \right)$, we get
${{\left( DC \right)}^{2}}=16\times 9$
$\Rightarrow DC=\sqrt{16\times 9}$
$\Rightarrow DC=\sqrt{16}\times \sqrt{9}$
$\Rightarrow DC=4\times 3$
$\Rightarrow DC=12cm$
$\Rightarrow DC=CD=12cm$
Note: In this question, we have to find a relation between the sides $AC$ and $BC$, whose lengths are already given in the question, so as to obtain the required side $CD$. That is why we have to prove similarity of the triangles to obtain a relation between the length of these sides.
In the above figure, let us consider $\Delta ADC$and $\Delta DBC$.
From the figure, we can see that the angle $C$ is common in both triangles. So, we can write
$\angle C=\angle C........\left( i \right)$
Also, there is a property of the circle which is related to the tangent and chord. This property states that
“the angle between the chord and the tangent is equal to the angle made by the chord in the alternative
segment”. Using this property in the above figure in $\Delta ADC$and $\Delta DBC$, we get
$\angle DAC=\angle BDC.......\left( ii \right)$
From equation $\left( i \right)$ and equation $\left( ii \right)$ , using $AA$ similarity rule, we get that
the triangles are similar.
$\Delta ADC\sim \Delta DBC$
Since these two triangles are similar, we can equate the ratio of corresponding sides of the
corresponding triangles. This means that we can equate the following sides,
$\dfrac{BC}{DC}=\dfrac{DC}{AC}$
$\Rightarrow {{\left( DC \right)}^{2}}=AC\times BC........(iii)$
It is given in the question that side $BC=9cm$.
We can see from the figure that $ABC$ is a straight line. So, we can obtain a relation as below,
$AC=AB+BC........(iv)$
Substituting values of $AB=7cm$ and $BC=9cm$ in equation $(iv)$, we get
$AC=7+9$
$\Rightarrow AB=7cm$
Substituting the values of $AC=16cm$ and $BC=9cm$ in equation $\left( iii \right)$, we get
${{\left( DC \right)}^{2}}=16\times 9$
$\Rightarrow DC=\sqrt{16\times 9}$
$\Rightarrow DC=\sqrt{16}\times \sqrt{9}$
$\Rightarrow DC=4\times 3$
$\Rightarrow DC=12cm$
$\Rightarrow DC=CD=12cm$
Note: In this question, we have to find a relation between the sides $AC$ and $BC$, whose lengths are already given in the question, so as to obtain the required side $CD$. That is why we have to prove similarity of the triangles to obtain a relation between the length of these sides.
Last updated date: 18th Sep 2023
•
Total views: 361.5k
•
Views today: 3.61k
